1. Introduction
Let
be a metric space and
with
. A geodesic path from x to y is an isometry
such that
. The image of a geodesic path is called a geodesic segment. A metric space X is a geodesic space if every two points of X are joined by a geodesic segment. A geodesic triangle
in a geodesic space X consists of three points
of X and three geodesic segments joining each pair of vertices. A comparison triangle of a geodesic triangle
is the triangle
in the Euclidean space
such that
for all
.
A geodesic space X is a CAT(0) space if for each geodesic triangle
in X and its comparison triangle
in
, the CAT(0) inequality
is satisfied by all
and
. The meaning of the CAT(0) inequality is that a geodesic triangle in X is at least as thin as its comparison triangle in the Euclidean plane. It is well-known that any complete and simply connected Riemannian manifold having non-positive sectional curvature is a CAT(0) space. Other examples of CAT(0) spaces include pre-Hilbert spaces, R-trees, Euclidean buildings. A complete CAT(0) space is called a Hadamard space.
Let C be a nonempty set and consider the following composite optimization problem: find
such that
(1)
where
are real-valued functions defined on C. This problem has a typical scenario in linear inverse problems, and it has applications in image reconstruction, machine learning, data recovering and compressed sensing (see [1] - [7] and the references therein).
In the case that X is a real Hilbert space or a real Banach space, problem (1) has been studied by many authors ( [3] [5] [8] - [12]). For example, in 2019, Chang et al. [8] used a modified hybrid algorithm to find a minimizer for problem (1) in Banach spaces without the assumption that the potential function is Fréchet differentiable and its gradient is L-Lipschitz continuous.
Recently, many convergence results for solving optimization problems have been extended from the classical linear spaces to the setting of manifolds. For example, in 2015, Cholamjiak-Abdou-Cho [13] established strong convergence of the sequence to a minimizer of a convex function and to a fixed point of nonexpansive mappings in CAT(0) spaces. Also in 2019, Chang et al. [14] presented a new modified proximal point algorithm for solving the minimization of a convex function and the common fixed points problem for two k-strictly pseudononspreading mappings in Hadamard spaces.
Recall that a mapping
is said to be
(i) nonexpansive, if
(ii) quasi-nonexpansive, if
and
(iii) k-strictly pseudononspreading, if there exists a constant
such that for all
(iv) demicontractive, if
and there exists
such that
Definition 1. An operator
is said to be pseudo-contractive if
Remark 1. The interest of pseudo-contractive operators lies in their connection with monotone mappings, namely, T is a pseudo-contraction if and only if
is a monotone mapping. It is well known that T is pseudo-contractive if and only if
Definition 2. An operator
is said to be quasi-pseudo-contractive if
and
(2)
From the above definitions, it is easy to see that the class of quasi-pseudo-contractive mappings is fundamental. It includes many kinds of nonlinear mappings such as the demicontractive mappings, the quasi-nonexpansive mappings and the k-strictly pseudononspreading with fixed points as special cases. Motivated by the researches above, we establish the convergent results to a minimizer of two convex functions and a common fixed point of quasi-pseudo-contractive mappings in Hadamard spaces. Thus our results generalize the corresponding results of Cholamjiak-Abdou-Cho [13], Chang et al. [14], Ariza-Ruiz et al. [15], Bačák [16], Dhompongsa et al. [17], Khan-Abbas [18] and many others.
2. Preliminaries and Lemmas
We now collect some elementary facts about CAT(0) spaces which will be used in the proofs of our main results. In 1976, Lim [19] introduced the concept of Δ-convergence in a general metric space. Recall that a sequence
in a CAT(0) space X is said to Δ-converge to
if x is the unique asymptotic center of
for every subsequence
of
. A geodesic space
is a CAT(0) space, if and only if
(3)
for all
and all
. Berg and Nikolaev [20] introduced the concept of quasilinearization as follows. Denote a pair
by
and call it a vector. Then quasilinearization is defined as a map
defined by
for all
. It is easy to see that
for all
. It is proved in [20] that a geodesically connected metric space is a CAT(0) space if and only if it satisfies the Cauchy-Schwarz inequality:
Lemma 1. [14] Let X be a Hadamard space. Then for all
and
, we have
(i)
(ii) 
(iii) 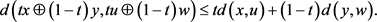
Definition 3. [14] Let C be a nonempty subset of a Hadamard space X and let  be a sequence in X. Then
be a sequence in X. Then 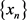 is Fejér monotone respect to C if
is Fejér monotone respect to C if
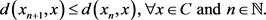
Lemma 2. [21] Let 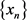 be a sequence in a Hadamard space X and let C be a nonempty subset of X. Suppose that
be a sequence in a Hadamard space X and let C be a nonempty subset of X. Suppose that 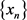 is Fejér monotone with respect to C and that every Δ-sequential cluster point of
is Fejér monotone with respect to C and that every Δ-sequential cluster point of 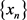 belongs to C. Then
belongs to C. Then  Δ-converges to a point in C.
Δ-converges to a point in C.
Lemma 3. Let C be a nonempty closed and convex subset of a Hadamard space X and 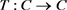 be an L-Lipschizian mapping with
be an L-Lipschizian mapping with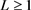 . Denote
. Denote
 (4)
(4)
If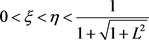 , then the following conclusions hold:
, then the following conclusions hold:
(i) 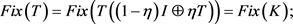
(ii) If  is demiclosed at 0, then
is demiclosed at 0, then  is also demiclosed at 0;
is also demiclosed at 0;
(iii) If T is quasi-pseudo-contractive, then the mapping K is quasi-nonexpansive, that is,

Proof. (i) If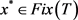 , it is obvious that
, it is obvious that![]() . Conversely, if
. Conversely, if![]() , i.e.,
, i.e., ![]() , letting
, letting![]() , then
, then![]() . Put
. Put![]() . Then
. Then![]() . Now we prove that
. Now we prove that![]() . In fact, we have
. In fact, we have
![]()
Since![]() , we have
, we have![]() , i.e.,
, i.e.,![]() . This shows that
. This shows that ![]() . It is obvious that
. It is obvious that ![]() if and only if
if and only if![]() . The conclusion (1) is proved.
. The conclusion (1) is proved.
(ii) For any sequence ![]() satisfying
satisfying ![]() and
and![]() . Next we prove that
. Next we prove that![]() . From conclusion (1), we only need to prove that
. From conclusion (1), we only need to prove that![]() . In fact, since T is L-Lipschizian, we get
. In fact, since T is L-Lipschizian, we get
![]()
which implies that
![]()
Since T is demiclosed at 0, we have![]() . The conclusion (2) is proved.
. The conclusion (2) is proved.
(iii) Since![]() , we have from (2)
, we have from (2)
![]() (5)
(5)
for all![]() . Since T is L-Lipschitzian, we get
. Since T is L-Lipschitzian, we get
![]() (6)
(6)
From (2) and (3), one has
![]() (7)
(7)
By (2) and (6), we obtain
![]() (8)
(8)
By (5), (7) and (8), we have
![]() (9)
(9)
Since![]() , we deduce that
, we deduce that![]() . From (9), one gets
. From (9), one gets
![]() (10)
(10)
for all ![]() and
and![]() . Combing (2) and (10) one has
. Combing (2) and (10) one has
![]()
which together with ![]() implies that
implies that
![]()
that is,
![]()
The proof is completed.
Now we consider the following problem: find a point ![]() such that
such that
![]() (11)
(11)
where C is a nonempty closed convex set of a Hadamard space X, ![]() are proper convex functions and
are proper convex functions and ![]() is a quasi-pseudo-contractive mapping. Recall that a function
is a quasi-pseudo-contractive mapping. Recall that a function ![]() is said to be convex, if for any geodesic
is said to be convex, if for any geodesic ![]() joining
joining![]() , the function
, the function ![]() is convex. If we set
is convex. If we set
![]()
then the problem (11) is equivalent to the problem of finding ![]() such that
such that
![]()
Define
![]()
It is easy to show that the bifunction ![]() has the following properties:
has the following properties:
(A1)![]() ;
;
(A2) F is monotone, i.e.,![]() ;
;
(A3) The function ![]() is convex for all
is convex for all![]() ;
;
Define a mapping ![]() by
by
![]()
Lemma 4. Let C be a nonempty closed convex subset of a Hadamard space X. Let F be a bifunction satisfying assumptions (A1)-(A3) and
(A4) For each ![]() and
and![]() , there exists a compact subset
, there exists a compact subset ![]() containing a point
containing a point ![]() such that
such that ![]() whenever
whenever![]() .
.
Then, the following conclusions hold:
(a) ![]() is well defined in X and
is well defined in X and ![]() is single-valued;
is single-valued;
(b) ![]() is firmly nonexpansive restricted to C, i.e.,
is firmly nonexpansive restricted to C, i.e., ![]() ,
,
![]()
(c)![]() , where
, where ![]() is the solution set of problem (1) (i.e., the set of minimizers of problem (1));
is the solution set of problem (1) (i.e., the set of minimizers of problem (1));
(d) For![]() , one has
, one has
![]() (12)
(12)
Proof. The result is a special case of Theorem 4 and Theorem 5 in [22], so we omit the proof here. ![]()
3. Δ-Convergence Theorems
We are in a position to give our main theorems. Throughout this section we assume that
(1) ![]() is a Hadamard space and C is a nonempty closed convex subset of X;
is a Hadamard space and C is a nonempty closed convex subset of X;
(2) ![]() are proper convex functions and the bifunction
are proper convex functions and the bifunction ![]() satisfies the assumption (A4);
satisfies the assumption (A4);
(3) ![]() is an L-Lipschitzian and quasi-pseudo-contractive mapping with
is an L-Lipschitzian and quasi-pseudo-contractive mapping with![]() ,
, ![]() is demiclosed at 0;
is demiclosed at 0;
(4) Denote
![]()
with![]() .
.
Theorem 1. Let ![]() be the same above. For any given
be the same above. For any given![]() , define the sequence
, define the sequence ![]() as follows:
as follows:
![]() (13)
(13)
where![]() ,
, ![]() are sequences in
are sequences in ![]() with
with ![]() . If the solution set
. If the solution set ![]() of problem (11) is nonempty, then the sequence
of problem (11) is nonempty, then the sequence ![]() Δ-converges to a point
Δ-converges to a point![]() , which is a minimizer of
, which is a minimizer of ![]() in C and also a common fixed point of
in C and also a common fixed point of ![]() in C.
in C.
Proof. Step 1. It follows from Lemma 4 (c) that if![]() , then
, then ![]() . Besides, by Lemma 3 (ii) we have
. Besides, by Lemma 3 (ii) we have ![]() is demiclosed at 0.
is demiclosed at 0.
Step 2. Next we prove that ![]() is Fejér monotone with respect to
is Fejér monotone with respect to![]() . In fact, by Lemma 4 (b),
. In fact, by Lemma 4 (b), ![]() is firmly nonexpansive, then it is nonexpansive. Let
is firmly nonexpansive, then it is nonexpansive. Let![]() , then one has
, then one has
![]() (14)
(14)
It follows from (13) and (14) that
![]() (15)
(15)
From (13), (14) and (15) we obtain
![]() (16)
(16)
which implies that ![]() is decreasing and bounded below. Thus the limit
is decreasing and bounded below. Thus the limit ![]() exists for each
exists for each![]() . It implies that
. It implies that ![]() is Fejér monotone with respect to
is Fejér monotone with respect to![]() . Without loss of generality, we can assume that
. Without loss of generality, we can assume that
![]() (17)
(17)
Therefore the sequence ![]() is bounded and so are the sequences
is bounded and so are the sequences ![]() .
.
Step 3. Now we prove that
![]() (18)
(18)
In fact, it follows from (12) that
![]() (19)
(19)
Hence in order to prove (18), it suffices to prove that![]() . Indeed, by (16) we get
. Indeed, by (16) we get
![]()
which can be rewritten as
![]()
which together with (17) implies that
![]() (20)
(20)
Combing (15) and (17) we obtain
![]()
which together with (20) implies that
![]() (21)
(21)
Also, by (15) we have
![]()
Then one gets
![]()
which together with (21) shows that
![]()
On the other hand, it follows from (14) that
![]()
These imply that![]() . Thus by (19) one has that the equality (18) holds.
. Thus by (19) one has that the equality (18) holds.
Step 4. In this step, we show that
![]()
In fact, it follows from (3), (13), (14) and Lemma 3 (iii) that
![]()
which together with (3), (13), (14) and Lemma 3 (iii) implies that
![]()
After simplifying and by using the condition that![]() , one gets
, one gets
![]()
which shows that
![]() (22)
(22)
Thus by (13) and (22), we get
![]() (23)
(23)
Furthermore, it follows form (18), (22) and (23) that
![]() (24)
(24)
Step 5. Finally, we prove that ![]() Δ-converges to some point
Δ-converges to some point![]() . Since in the second step, we have shown that
. Since in the second step, we have shown that ![]() is bounded in C and it is Fejér monotone with respect to
is bounded in C and it is Fejér monotone with respect to![]() . Then by Lemma 2, in order to prove
. Then by Lemma 2, in order to prove ![]() Δ-converges to some point in
Δ-converges to some point in![]() , it suffices to show that every Δ-sequential cluster point of
, it suffices to show that every Δ-sequential cluster point of ![]() belongs to
belongs to![]() .
.
In fact, let ![]() be a Δ-sequential cluster point of
be a Δ-sequential cluster point of![]() , then there exits a subsequence
, then there exits a subsequence ![]() of
of ![]() Δ-converging to
Δ-converging to![]() . From (18) and (23), it follows that
. From (18) and (23), it follows that ![]() and
and![]() . Since
. Since ![]() is nonexpansive,
is nonexpansive, ![]() is demiclosed at 0. Note that
is demiclosed at 0. Note that ![]() and
and ![]() are also demiclosed at 0 by Lemma 3 (ii). Now by (24) and Lemma 3 (i), we obtain
are also demiclosed at 0 by Lemma 3 (ii). Now by (24) and Lemma 3 (i), we obtain ![]() . Therefore, by Lemma 2,
. Therefore, by Lemma 2, ![]() Δ-converges to some point in
Δ-converges to some point in![]() . The proof is completed.
. The proof is completed. ![]()
4. Strong Convergence Theorems
Let ![]() be a Hadamard space and C be a nonempty closed convex subset of X. Recall that a mapping
be a Hadamard space and C be a nonempty closed convex subset of X. Recall that a mapping ![]() is said to be demi-compact, if for any bounded sequence
is said to be demi-compact, if for any bounded sequence ![]() in C such that
in C such that ![]() (as
(as![]() ), then there is a subsequence
), then there is a subsequence ![]() such that
such that ![]() converges strongly (i.e., in metric topology) to some point in C.
converges strongly (i.e., in metric topology) to some point in C.
Theorem 2. Let all the conditions in Theorem 1 be satisfied and ![]() be demi-compact restricted to C, then the sequence
be demi-compact restricted to C, then the sequence ![]() defined by (13) converges strongly to a point
defined by (13) converges strongly to a point![]() .
.
Proof. Indeed, since ![]() is demi-compact restricted to C, it follows from (24) that there is a subsequence
is demi-compact restricted to C, it follows from (24) that there is a subsequence ![]() such that
such that ![]() converges strongly to some point
converges strongly to some point![]() . Since
. Since ![]() is demiclosed at 0, we have
is demiclosed at 0, we have![]() .
.
Moreover, it follows from (18) and (23) that ![]() and
and ![]() as
as![]() . Since
. Since ![]() is demi-closed at 0, by (24) we have
is demi-closed at 0, by (24) we have ![]() . Hence
. Hence![]() . Besides, it follows form (17) that
. Besides, it follows form (17) that ![]() exists. Thus we get
exists. Thus we get![]() . The proof is completed.
. The proof is completed. ![]()
Theorem 3. Suppose that all the conditions in Theorem 1 are satisfied. Moreover, let ![]() be a nondecreasing function with
be a nondecreasing function with ![]() and
and
![]() (25)
(25)
then the sequence ![]() defined by (13) converges strongly to a point
defined by (13) converges strongly to a point![]() .
.
Proof. It follows form (24) and (25) that
![]()
Since ![]() is nondecreasing with
is nondecreasing with ![]() and
and![]() , we have
, we have
![]()
which implies that
![]()
Hence ![]() is a Cauchy sequence in C. Noting that C is closed and convex in the Hadamard space X, C is also complete. Without loss of generality, we can assume that
is a Cauchy sequence in C. Noting that C is closed and convex in the Hadamard space X, C is also complete. Without loss of generality, we can assume that ![]() converges strongly to some point
converges strongly to some point![]() . Then
. Then ![]() . Besides, since
. Besides, since ![]() is quasi-nonexpansive and
is quasi-nonexpansive and ![]() is nonexpansive, it is clear that
is nonexpansive, it is clear that ![]() is closed in C. Thus we get
is closed in C. Thus we get![]() . The proof is completed.
. The proof is completed. ![]()
5. Conclusion and Remarks
Let us conclude this paper with some open questions whose answers might largely improve the applicability of the results in this present paper.
Question. Whether or not we can improve the (A4) condition: For each ![]() and
and![]() , there exists a compact subset
, there exists a compact subset ![]() containing a point
containing a point
![]() such that
such that ![]() whenever
whenever![]() , in order to obtain similar results regarding the resolvent operator
, in order to obtain similar results regarding the resolvent operator![]() ?
?
Acknowledgements
The author would like to thank the referees for their pertinent comments and valuable suggestions.