A Revised Interpretation of the Thermodynamic Theory Including the Einstein Mass-Energy Relation E = mc2 ()
1. Introduction
1.1. Brief Review of the Concepts of Reversibility and Irreversibility
The system we are considering (Figure 1) is a gas contained in a cylinder permeable to heat (i.e. diathermal), and equipped with a mobile frictionless piston, which is also diathermal. In state 1, the external pressure Pe and the internal pressure Pi (pressure of the gas) have the same value P1. Then, due to the deposition of a mass of sand on the piston, Pe passes from the value P1 to a value P2, and the piston moves down with the consequence that, in state 2, Pi also reaches the value P2.
![]()
Figure 1. Irreversibility and reversibility.
The sand can be deposited very rapidly (i.e. all at once) or very slowly (i.e. in several successive small batches).
In the first case, Pe reaches immediately the value P2, while Pi reaches this value only when the piston stops. It is well known that this situation is designated irreversibility in the sense that Pe and Pi are always different during the process. In such conditions, the work done on the gas by the piston, for an elementary change in volume noted dV, must be written
(1)
In the second case, by contrast, the pressure exerted by the piston passes very gradually from the initial value P1 to the final value P2, with the consequence that, at each moment of the process, Pe and Pi can be considered as equal. This situation is designated reversibility and, in such conditions, the elementary work done on the gas, by the piston, is given by the relation:
(2)
For a given value of dV, the difference between dWirr and dWrev takes the form:
(3)
that can also be written:
(4)
Referring to Figure 1, it appears that we have dV > 0 when Pi > Pe and dV < 0 when Pi < Pe. (this second situation being the one illustrated by the diagram). As a consequence, the term
obeys in all cases the condition:
(5)
meaning itself that we have always:
(6)
Another possible expression of Equation (4) is therefore:
(7)
where dWadd can be regarded as an additional energy representing the difference between dWirr and dWrev and obeying the condition:
(8)
In practice, it is well known that the additional energy, noted here dWadd, mainly appears in the form of heat, classically designated dQ, that is evacuated towards the surroundings. This heat evacuation explains that the final temperature of the gas has in fact the same value as its initial temperature, that is also the temperature of the surroundings.
1.2. Remarks Concerning the First Law of Thermodynamics
For the matter that will be discussed in this paper, the information we need about the first law is summarized in Equations (9), (10), (11), (12), and (13) given below.
The first law of thermodynamics is a postulate which consists in admitting that when a system passes from a determined state 1 to a determined state 2, its internal energy variation, noted dU, always obeys the relation:
(9)
If the energy exchanges are limited to work (W) and heat (Q), the detailed meaning of Equation (9) takes the form:
(10)
If the system taken in consideration is isolated, the complementary precision given by the first law is that Equations (9) and (10) become respectively:
(11)
(12)
Knowing that an isolated system has no exchanges of energy with its surroundings, all the terms of Equations (11) and (12) refer to energy exchanges occurring inside the system.
We have seen with Equation (6) that dWirr and dWrev obey the general relation:
(R.6)
Combining this data with the information given by Equations (9) and (10), leads to the conclusion that the terms dQirr and dQrev must themselves obey the relation:
(13)
In thermodynamic textbooks, the considerations concerning dQ are generally discussed in the chapters dealing with the second law. We will now enter in this context in order to see if the relation dQirr < dQrev given by Equation (13) can really be verified.
1.3. Remarks Concerning the Second Law of Thermodynamics
As was the case for the first law, the concepts of reversibility and irreversibility remain of fundamental importance for the understanding of the second law, but they are associated here with the complementary concept called entropy. Its presentation is often done in the following condensed form.
In conditions of reversibility, a change in entropy (noted dS) is linked to a change in heat (dQ) and to the absolute temperature (T) by the relation:
(14)
In conditions of irreversibility the corresponding relation becomes:
(15)
When we discover these equations for the first time and receive the complementary information that dS has the same value in both cases (because S is a state function, as well as V, the volume), we are tempted to think that dQ represents dQrev in Equation (14) and dQirr in Equation (15). With this idea in mind, we are led to deduce that these terms obey the relation:
(R. 13)
which is the one suggested by Equation (13), at the end of the previous section.
At this stage of the presentation, the reasoning seems coherent and easily understandable. The problem is that the relation dQirr < dQrev is not confirmed when we examine the numerical applications presented as examples of the use of these equations (one of them, very simple, is mentioned below in paragraph 2.2).
The reason is due to the fact that, in this context, we discover that the precise meaning of Equation (14) is really:
(16)
but the precise meaning of Equation (15) is interpreted as being:
(17)
complemented by the information that the term dSi, designated as the internal component of entropy, has always a positive value and therefore can always be written:
(18)
A related piece of information is that the term dS = dQ/Te is designated dSe and called the external component of entropy, so that a condensed writing of Equation (17) is:
(19)
Although the term dQ of Equation (15) is sometimes designated dQirr in thermodynamics textbooks, the numerical value given to dQ in Equation (17) is really dQrev, as will be seen further with Equation (28) that refers to a typical numerical example.
The conclusion which follows from this observation is that the term dQirr is not present in the equations going from number 14 to number 19, so that its comparison with the term dQrev is not possible at the moment.
The situation was different for the comparison between the terms dWirr and dWrev introduced in paragraph 1 because their definitions, given by Equations (1) and (2), were directly presented in the form of energy equations.
To obtain the conversion of the entropy equations (16) and (17) into energy equations, the solution consists in multiplying both terms of Equation (16) by Ti, and the three terms of Equation (17) by Te. The results are:
For Equation (16):
(20)
For Equation (17)
(21)
whose meaning is
(22)
In the same manner as, in Equation (7), we have designated dWadd the term representing the difference dWirr – dWrev, we can here adopt the designation dQadd for the term TedSi, so that an alternative writing of Equation (22) is:
(23)
Having noted with Equation (17) that dSi is always positive and knowing that the same is true for Ti and Te (because, in thermodynamics, temperatures are always expressed in Kelvin), the term TedSi, also noted dQadd is itself positive. Consequently, it can be derived from Equation (23) that dQirr and dQrev are linked together, not by the relation dQirr < dQrev presented above as the expected one (Equation (13)), but by the inverted relation, that is:
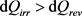 (24)
(24)
2. Discussion: Consequences of These Observations on the Understanding of the Theory
2.1. Preliminary Remark
If we accept the proposal dQirr > dQrev given by Equation (24) and at the same time the proposal dWirr > dWrev given by Equation (6), their addition leads to the proposal:
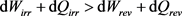 (25)
(25)
which disagree with the proposal 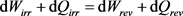 presented in Equation (10) as the conventional understanding of the first law of thermodynamics.
presented in Equation (10) as the conventional understanding of the first law of thermodynamics.
The situation is similar if the addition of Equations (24) and (6) is entered in Equations (11) and (12), because the result obtained would mean that an isolated system can be concerned by a positive variation of its internal energy (dUirr > 0).
Despite the fact that such a proposal appears impossible in the conventional approach of thermodynamics, it becomes easily understandable if the mass-energy relation is taken into account. Two reasons may explain why it has not been done previously. The first one is that at the time of the discovery of the laws of thermodynamics, the theory of relativity was not known. The second is that even without the help of the mass-energy relation, the efficiency of the thermodynamic tool is indisputable, so that no urgency was felt to revise the interpretation of its laws. Nevertheless, it seems that the theory gets more easily understandable when this complement is added and perhaps the scope of its applications may be extended.
2.2. Analysis of a Heating Process Concerning a Closed System
For an easy approach of the matter, let us examine the situation below, presented in a basic thermodynamic course as an example of use of the concept of entropy. The system is defined as 1000 g of water (1 liter) that are heated from 20˚C (293 K) to 80˚C (353 K), by contact with a thermostat at 80˚C (353 K), under atmospheric pressure. The asked question concerns the determination of the terms ΔQ, ΔS, ΔSe and ΔSi, knowing that the specific heat capacity of water is cpwater = 4,184 JK−1∙g−1 that can be admitted constant over the temperature range.
The answers, equally given in the course, are as follows:
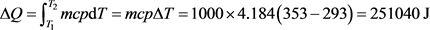 (26)
(26)
 (27)
(27)
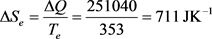 (28)
(28)
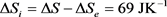 (29)
(29)
So far, these results do not raise ambiguity whether the hypothesis to which we refer is the classical interpretation or the new suggested one. The divergence begins when the asked question is in knowing whether the term ΔQ, mentioned in Equation (28) means ΔQirr or ΔQrev. The interest of the question comes from the fact that in the classical approach, the relation between both terms is the inequality dQirr < dQrev given by Equation (13), while in the new suggested hypothesis, it is the inequality dQirr > dQrev given by Equation (24).
In the first hypothesis, the question is considered useless for the example presently examined, because the formulation of the first law being dUirr = dUrev, it reduces to dQirr = dQrev when the energy exchange is limited to heat. This is practically the case here, since the work due to change in volume of the water heated from 20˚C to 80˚C can be considered negligible, compared to the change in heat, so that we can write dW = 0.
The situation is not the same in the second hypothesis because the conversion of the Entropy Equation (17) into the Energy Equation (21) introduces a real difference between dUirr and dUrev and consequently between ΔQirr and ΔQrev although the change in volume is always considered negligible.
To know the exact meaning of the term noted ΔQ, the criterion to take into account is that its value is independent of the degree of irreversibility of the heating process when it represents ΔQrev, while it is not the case when it represents ΔQirr. To make a test using this criterion, we may imagine a division of the heating process in two steps noted A and B, the first one from 293 K to 223 K, the second from 223 K to 253 K. Reproducing the calculation presented above and adding the obtained results, we are led to the following table:
 (30)
(30)
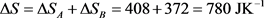 (31)
(31)
 (32)
(32)
 (33)
(33)
Through these results, it can be effectively observed that the division of the heating process in two steps has no effect on the values of ΔQ and ΔS, but increases the value of ΔSe (change from 711 to 744 JK−1) and decreases that of ΔSi (change from 69 to 36 JK−1). If the number of steps is multiplied, we easily conceive that the value ΔSi tends progressively towards zero, meaning that the heating process tends towards reversibility. The question asked above is therefore answered in the sense that ΔQ represents here ΔQrev and the corresponding term ΔQirr can be calculated by Equation (22), whose differential and integrated formulations are respectively:
 (R. 22)
(R. 22)
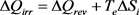 (34)
(34)
Applying Equation (34) to the considered system leads to the following observations:
When the heating process is done in a single step, we have:
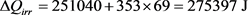 (35)
(35)
When it is done in two steps, we have:
 (36)
(36)
Being lower than the previous one, this last value concerns effectively the term ΔQirr which decreases progressively and tends towards ΔQrev (itself remaining constant) when the number of steps is multiplied. Thanks to this difference of behavior, the problem of the identification of ΔQirr and ΔQrev is solved.
The reason why this procedure is not used in thermodynamic courses is evidently that the conclusion ΔQirr > ΔQrev to which it leads it is not in accordance with the usual understanding of the first law. As mentioned above, this last one implies the general equality ΔUirr = ΔUrev which becomes ΔQirr = ΔQrev when the energy exchange is limited to heat, as it is the case here. Referring to this situation, it can be observed that the strict obedience to the conventional understanding of the first law reduces the information given by the second law, because it does not allow the conversion of the entropy Equation (17) to the energy Equation (21). In close relation with this remark, some additional suggestions are discussed below.
If we group together Equations (20), (21) and (22) which are respectively:
 (R. 20)
(R. 20)
 (R. 21)
(R. 21)
![]() (R. 22)
(R. 22)
we see that the terms dQirr and dQrev can be directly defined by the energy formulations:
![]() (37)
(37)
![]() (38)
(38)
The entropy being a state function, as the volume, the differential dS has the same value in both equations. Therefore we can write:
![]() (39)
(39)
i.e.
![]() (40)
(40)
The terms Te and Ti being positive (absolute temperatures), we also see from Equations (37) and (38) that dS and dQ have the same sign. The term dQ being positive when Te > Ti and negative when Te < Ti, the same is true for dS. Consequently, the term ![]() is always positive, confirming the relation:
is always positive, confirming the relation:
![]() (R. 24)
(R. 24)
As already done for dWirr, with Equation (7), we can give to this last equation the expression:
![]() (41)
(41)
where the term dQadd is positive.
Then adding the relations ![]() (Equation (41)) and
(Equation (41)) and![]() , (Equation (7)), we get the global result:
, (Equation (7)), we get the global result:
![]() (42)
(42)
whose meaning is:
![]() (43)
(43)
2.3. Analysis of a Heat Exchange Occurring inside an Isolated System
Let us imagine now, the case of an isolated system made of two parts 1 and 2 separated by a diathermic wall. Supposing that part 1 is defined as 1 liter of water at 20˚C and part 2 as 1 liter of water at 80˚C, our objective is the analysis of their exchange of energy.
A first idea that comes to mind is that, just after the end of this exchange, both parts will be at the same final temperature Tf = 50˚C, (= 323 K). If a thermometer is placed in each of them, this result can be verified directly, but can also be predicted by the well-known equation:
![]() (44)
(44)
which gives Tf = 323 K (taking into account that C1 = m1c1 and C2 = m2c2).
Designating Ti the initial temperature and Tf the final temperature, the main elements of the calculation are given below.
For the terms ΔQrev1, ΔQrev2 and ΔQrev syst, we get:
![]() (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
For the terms ΔS1, ΔS2 and ΔSsyst:
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
For the terms ![]() and
and ![]() representing the average temperatures of part 1 and part 2:
representing the average temperatures of part 1 and part 2:
![]() (51)
(51)
![]() (52)
(52)
For the terms ΔQirr1, ΔQirr2 and ΔQirr syst:
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
In the conventional approach of the theory, the only results taken in consideration for the whole system are ΔQsyst = 0 (Equation (47)), where ΔQsyst means indifferently ΔQrev syst or ΔQirr syst and ΔSsyst = 36 JK−1 (Equation (50)).
In the revised approach that is proposed here, we see that a distinction is made between the term ΔQrev syst = 0, and the term ΔQirr syst > 0, whose calculated value is ΔQirr syst = 23328 J.
The reader accustomed to the usual approach of the theory may be tempted to consider this last result as irrealist, because it seems impossible that an energy can be created inside an isolated system. Before examining below the possibility of a link between thermodynamics and relativity, the attention is called to the following remark, briefly evoked in the abstract.
Taking into account that thermodynamics is among the most synthetic theories of physics and the relation E = mc2 among the most general equations of science, we may be astonished that this latter is not explicitly present in the laws of thermodynamics. Perhaps it is hidden behind our habit of giving the first law the meaning dUirr = dUrev instead of dUirr > dUrev? It is on the basis of this idea that the considerations discussed in the following paragraph are based.
3. The Link between Thermodynamics and Relativity
The first evocation of a link between thermodynamics and relativity seems to have been advanced by R. C. Tolman in 1928 [1]. At the sight of a photo nowadays presented in Wikipedia [2], one can imagine that he had the opportunity to discuss this subject with A. Einstein, all the more that they were co-authors of several articles. In the following years, many other authors have published on the same topic, their contributions being generally addressed to readers having a strong background in physics and mathematics. Some recent ones, quoted below in the section References, were written by H. Callen and G. Horwitz [3], Y. Rengui [4], S. A Haywards [5], C. A. Farias, P. S. Moya and V. A. Pinto ( [6], M. Requart [7], R. C. Gupta, R. Gupta and S. Gupta [8], T. Yarman, A. L. Kholmetskii and J-L Tane [9], V. Krasnoholovets and J-L. Tane [10].
From the observations reported in the present paper, the first information to keep in mind is that there is always a difference between the terms dQirr and dQrev, even when the energy exchange concerning the considered system is limited to heat. The second information is that this difference always obeys the condition dQirr > dQrev. Added to the condition dWirr > dWrev (Equation (6)), we get the relation dUirr > dUrev (Equation (43)) which seems more appropriate than the proposal dUirr = dUirr (Equation (9)) in the role of fundamental postulate attached to the first law.
The hypothesis already suggested in several papers (J-L. Tane [11] [12] [13] [14] [15]) is that the inequality dQirr > dQirr , written above (Equation (41)) under the expression:
![]() (R. 41)
(R. 41)
can be interpreted as having the meaning:
![]() (56)
(56)
where c2dm is the differential form of the mass-energy relation E = mc2. The sign ± means than the choice between + and − is not done for the moment and will be examined further.
The term dUadd having been described above as omnipresent in thermodynamic processes, its assimilation to the term c2dm is a way to say that thermodynamics and relativity are closely associated. In science education, this idea is not yet totally integrated. This can be seen from the fact that processes involving a detectable change in mass, such as nuclear reactions, are rarely interpreted from a thermodynamic point of view. Correlatively, numerical examples presented in thermodynamics books are almost never devoted to nuclear reactions.
This situation reminds us that thermodynamic systems are classically divided into three categories, depending on whether they are open, closed, or isolated. Before the discovery of relativity, it was admitted that only open systems can be affected by a change in mass. After this discovery, the same possibility has been extended to closed systems. Perhaps will it be equally extended to isolated systems in the future?
In a book of thermodynamics for earth scientists recently written by G. M. Anderson [16], the mass-energy relation E = mc2 is mentioned, with the remark that its practical use is mostly impossible, since the changes in mass are too small to be measurable. Referring to the context evoked above (isolated system made of two liters of water designated 1 and 2 that have a mutual heat exchange) there is no doubt that the change in mass is not detectable. Despite this state of affairs, the problem seems of great interest from the theoretical point of view.
The starting reason is that the change in mass that can be predicted is not the same, depending on whether we adopt the classical approach of the theory or the new suggested one. In the first case, the heat exchange will be characterized by the relation ΔQ1 = −ΔQ2, (Equations (45) and (46)) implying Δm1 = −Δm2 and consequently Δmsyst = 0. In the second case, having obtained ΔQirr1 ≠ −ΔQirr2 (Equations (53) and (54)), we will get Δmsyst ≠ 0 and the remaining question is the choice between Δmsyst > 0 and Δmsyst < 0 for the corresponding change in mass.
In the same way as, in paragraph 1, the energy initially designated dWadd (Equation (8)) was not really work, but heat, the energy noted ΔQirr syst = 23328 J (Equation (56)) is not really heat but another kind of energy. It is not heat because the experimenters never reported that an exchange of heat between two parts of an isolated system have led to a final temperature exceeding the value given by Equation (44). Being generated inside the system, the possible solution is that ΔQirr syst is a potential energy of gravitation, whose origin is a decrease in mass of the system. Referring to the mass-energy relation this explanation corresponds to the formulation dE = −c2dm which means that Equation (56) would itself be written:
![]() (57)
(57)
This equation would keep the same form for a system containing other materials than water. Transposed at the scale of a very large system, the presence of the term c2dm, implies a possible gravitational effect, which cannot be taken into account when the basis for discussion is the equality dUirr = dUrev instead of Equation (57). Preliminary comments concerning this question are presented in reference [15], with the possibility that the decrease in mass contributes to increase the Earth-Moon distance. Correlatively, the possibility is evoked in reference [17] that, for living systems, Equation (57) could be substituted by equation:
![]() (58)
(58)
Remaining in the context of systems made of inert matter (objects of the experiments that have inspired the laws of thermodynamics), another interesting question is the relation between c2dm and the function Gibbs Free Energy. Designated G, in honor of its discoverer Josiah Willard Gibbs, its definition is:
![]() (59)
(59)
giving, by differentiation:
![]() (60)
(60)
which can also be written:
![]() (61)
(61)
From the analysis presented above, the meaning of Equation (61) can be imagined as being:
![]() (62)
(62)
whose detailed writing becomes:
![]() (63)
(63)
If the considered process is carried out at constant temperature Te and constant pressure Pe, the terms dTe and dPe are nil and this last equation is reduced to:
![]() (64)
(64)
whose condensed formulation is really:
![]() (65)
(65)
Then knowing from Equation (57) that ![]() and entering this value in Equation (65), we get for the precise meaning of dG:
and entering this value in Equation (65), we get for the precise meaning of dG:
![]() (66)
(66)
For reason of convenience, the practical use of the term dG is not the one given by relation ![]() (Equation (65)) but by a relation that can be written very schematically:
(Equation (65)) but by a relation that can be written very schematically:
![]() (67)
(67)
where “ref” means “references” and “real” means “real”. In the study of chemical reactions, the conditions of references are generally T = 298 K and P = 1 bar.
Although the term c2dm is not explicitly written in equations such as 65 or 67, it is always implicitly present since ![]() (Equation (57)) and therefore it plays a fundamental role for the understanding of the thermodynamic theory.
(Equation (57)) and therefore it plays a fundamental role for the understanding of the thermodynamic theory.
Among the recent books intended to underline the omnipresence of equation E = mc2 around us and in the universe, is that of C. Galfard [18].
4. Conclusions
Because my scientific specialty is not physics, but geology, I discovered thermodynamics late and with the precious help of books specially written for geologists. I have greatly appreciated that in some of them [19] [20], the idea was evoked that perhaps something remains to be clarified in the theory. As already noted, the existence of a link between thermodynamics and relativity seems all the more probable that the mass-energy relation E = mc2 is known to be one of the most general equations of science while, in the same time, it is almost never used in thermodynamics textbooks.
Being limited to the macroscopic approach of thermodynamics, and the use of a basic mathematical tool, the hypothesis suggested in this paper seems easily accessible to a wide scientific readership. My hope is that it can be recognized useful by specialists and that the conversion of the entropy Equation (17) into the energy Equation (21) can be accepted in the future by authors of thermodynamics textbooks.
Acknowledgements
I would like to thank the readers who sent me comments (generally positive) about my previous papers on this matter.