1. Introduction
Currently, the world faces global warming challenges due mainly to fossil fuel power generation [1]. The power generation using renewable energy has been developed as a solution to global warming challenges. Among renewable energy power sources, wind power has been attracting more attention. Wind power generation has the advantage of low power generation costs and high conversion efficiency compared with other renewable sources. In most of the development new megawatt-scale wind turbines is of variable speed using either a permanent magnet synchronous generator or a doubly fed induction generator. Back-to-back converters for variable speed wind turbines are installed between the wind generator and the grid [2]. The grid-connected inverters for variable speed wind turbines have a small output power limit, no damping, no synchronous power, and no inertia. Typically, a grid system has synchronous generators with synchronizing power and inertia. They are able to provide active power and reactive power dynamically to keep the grid voltage and frequency constant.
The virtual synchronous generator is a method that provides virtual inertia and synchronous power to interconnected inverters [3]. Virtual inertia can be established in a distributed generator, for example, a renewable energy source using a power electronics inverter and a converter with a current-control system. This method is called a virtual synchronous generator or an asynchronous virtual machine. In 2007, the Virtual Synchronous Generator research group focused on a current-reference emulated inertia provided by a phase lock loop (PLL) for a rotating frame for the dq control of an inverter.
The virtual synchronous generator of the Institute of Electrical Power Eng. (IEPE) at Clausthal University of Technology in Germany is based on a simplified synchronous generator model. A reference current (voltage) of this method is provided from the grid voltage (current). This method helps to improve the frequency stabilization in short time. Furthermore, this method allows voltage source converters to be connected to a weak grid system by the PLL synchronizing technique.
A study of a wind diesel system with a short-term energy storage system (ESS) controlled as a virtual inertia and a virtual synchronous generator was presented in [4]. Their ESS controller as a virtual inertia can enhance the dynamic frequency stability of a small scale grid under fluctuating renewable energy and load fluctuations. The optimized variable inertia is introduced in the virtual inertia method which can improve the grid frequency response with lower power compared to the conventional fixed virtual inertia method.
The study in [5] demonstrated a model for a grid-following and grid-forming virtual inertia converter for a low inertia grid system. A grid-following virtual inertia converter is controlled to output active power proportional to the frequency deviation and rate of change of frequency estimated by a PLL. However, the grid-forming virtual inertia converter uses a voltage source connected to the grid through an LC filter of which the output voltage is based on the angle which is the function of power in feed of the virtual inertia converter.
Most of them use PI control scheme in the rotating frame for current (voltage) control of the converter. We propose a model-following control for the interconnected inverter [6] [7] [8]. The model-following controlled inverter can follow the reference model more accurately than the conventional method. The basic configuration is to output power from the voltage inverter connected to the grid through a filter, in a similar way to a grid-forming virtual inertia converter. The method presented in this paper follows reference current by instantaneous control with emulating not only inertia but also synchronous power based on the simple synchronous generator model. There is no control delay resulting from PLL, because PLL is not required for instantaneous value control.
This paper is organized as follows: Chapter 2 describes a discrete-time model-following control (DMFC) system consisting of the virtual synchronous generator model, an inverter grid model and a state feedback gain. The simulation results and discussions of the proposed controller are provided in Chapter 3. Finally, Chapter 4 describes the conclusion.
2. Proposed Novel Current Controller
2.1. Discrete Time Model Following Controller
This chapter describes the discrete-time model following control system.
Figure 1 shows a grid connected inverter with an LCL filter for a wind generator.
This inverter system comprises a wind turbine, a three-phase diode rectifier, a three-phase full-bridge PWM inverter, and an LCL filter installed between the inverter and the grid voltage with the equivalent grid system impedance.
Figure 2 shows a diagram of the discrete time model following system. The system shown in Figure 2 is a hybrid system consisting of the continuous-time plant system, the discrete time virtual synchronous generator model, and the discrete-time state feedback gain.
The state feedback gain is derived next. The extended system equation used to derive the state feedback gain is given by
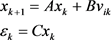(1)
Commonly, models are not always reachable. Thus, the model space is often broken down into reachable model space and non-reachable model space. Equation (1) can be rewritten as follows:
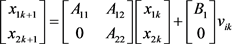(2)
![]()
Figure 1. Wind turbine system with grid connected inverter.
![]()
Figure 2. Discreat-time model following controller with virtual synchronous generator.
where the state vector with a reachable space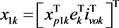
, a state vector with a non-reachable space
; a plant state vector
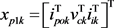; the output current vector of the virtual synchronous modelivok; the LCL filter output current vector ipok; the capacitor voltage vector of the LCL filter vck; the input current vector of the LCL filter iik; a non-reachable state vector of the virtual synchronous model
; the rotation speed of a virtual synchronous generator ωgk; the unit vector of the no-load induced voltage ek; and the input voltage vector of LCL filter vik. Cpd1 is defined by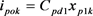 
,
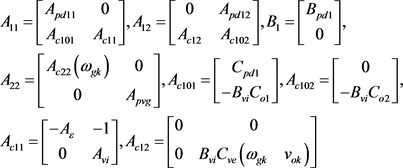(3)
The quadratic evaluation function is given by:
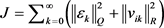(4)
In this case, the optimal input is given by:
(5)
where P is a solution of the following Riccati equation.
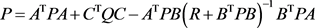(6)
Matrix P is divided into four sub-matrixes.
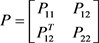(7)
Because the lower submatrix of matrix B is a zero-matrix, the optimal input is as follows:
(8)
It should be noted that the above equation is used for only P11 and P12.
Thus, there is a solution that satisfies the following:
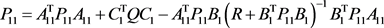(9)
P12 can also be obtained from the following equation.
(10)
The virtual synchronous generator model is nonlinear, and the rotor speed of the virtual synchronous generator model changes with time. Therefore, this optimal input may be a derivative in each discrete-time interval.
2.2. Grid Connected Inverter
The plant system shown in Figure 3 shows a block diagram of the wind turbine system with discrete-time model following controller.
In this paper, the three phase circuits are assumed to be symmetrical. Thus, the plant system can be shown using only a single phase. An inverter with the wind generator is simulated with an ideal voltage source.
A continuous-time plant is composed of an inverter LCL filter, an impedance of the grid system, and a voltage source, which simulates the power system.
The plant system is described as follows:
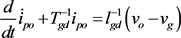(11)
![]()
(12)
![]()
(13)
![]()
(14)
where ipo (instantaneous current [A] divided by the base current [A]) is the output current vector of the LCL filter composed of a zero-sequence current, a
![]()
Figure 3. Single phase circuit of the three phase grid connected inverter with LCL filter.
positive-sequence current and a negative-sequence current; ii is the input current vector of the LCL filter; vc (instantaneous voltage [V] divided by the base voltage [V]) is a star-connected capacitor voltage vector of the LCL-filter; vi is a filter input voltage vector; vg is the voltage vector of the equipment grid voltage; and cY (capacitor [F] multiplied by the base capacitance [F]) is the capacitor matrix of the three phases, which are assumed to be symmetrical. Let l1 (inductance [H] divided by the base inductance [H]) be the inductance matrix in the filter input side and T1 be the time-constant matrix. In addition, lgd is the inductance matrix of the equivalent grid system, and Tgd is the time constant matrix.
Combining Equations (11) and (12) gives the following equation.
![]()
(15)
The grid voltage vector vg is given as follows:
![]()
(16)
![]()
(17)
where v is the unit vector of the grid voltage. The grid voltage magnitude |vg| is constant. ωbase is the nominal grid frequency and Sαβ is the following skew matrix.
![]()
(18)
By assuming that vi and vg are constant during the time interval Ts [sec], and vik and vgk, are given, the discrete-time system is derived using Equations (13)-(17) as follows:
![]()
(19)
![]()
(20)
![]()
(21)
![]()
(22)
![]()
(23)
The plant system equation is as follows:
![]()
(24)
where; the plant system state vector![]()
, and the filter input voltage vector vik is the plant system input vector.
2.3. Virtual Synchronous Generator Model
The equation of the motion of the virtual synchronous generator is given below:
![]()
(25)
where Mg [s] is the virtual synchronous generatorinertia constant (twice the stored energy constant, H), Tg [s] isa mechanical time constant, ωg [rad/s] is the rotor speed, Pi [pu] is the input power, Po [pu] is the output power, and ωbase [rad/s] is the rated rotor speed. Since the virtual synchronous generator is assumed to have two poles, the rated rotation speed is equal to the rated frequency of the grid system.
If the rotor speed is ω(= ωg/ωbase) [pu], the input torque τi [pu] (the output torque τo [pu]) becomes τi = Pi/ω(τo = Po/ω), so that the Equation (25) becomes as follows.
![]()
(26)
The power input is composed of a reference output power and a speed governor component, as shown below:
![]()
(27)
where Kgov is the governor gain, and ![]()
is the reference of the output power.
The equation of the electrical circuit of the virtual synchronous generator is given as follows:
![]()
(28)
where Tvo [s] is the virtual synchronous generator electrical time constant matrix, lg is the synchronous inductance matrix, ivo is the output current vector of the virtual synchronous generator, vo is the output voltage vector, and eg is the no-load induced voltage vector.
The voltage vector eg is given as follows:
![]()
(29)
![]()
(30)
where e is the unit vector of the no-load induced voltage. The no-load induced voltage magnitude ![]()
is a time-variant value.
The proportional output voltage regulator gives the no-load induced voltage magnitude ![]()
as:
![]()
(31)
where ![]()
is the reference value of the no-load induced voltage. ![]()
is reference value of the output voltage. Kavg is the proportional gain of the voltage regulator.
The output voltage vo can be obtained as follows by subtracting Equation (11) and Equation (12).
![]()
(32)
The above equation is replaced by the following discrete-time matrix equation.
![]()
(33)
If Po and Pi take constant values of Pok and Pik, during the time interval Ts [s], the discrete-time system is derived using the Equation (26), (28), (29) and (30), as follows:
![]()
(34)
![]()
(35)
![]()
(36)
![]()
(37)
3. Simulation Result
3.1. PI Current Controller
In this chapter, a current controlled inverter using a rotating frame for a dq transformation and applied by the provided virtual synchronous generator model, is described.
Figure 4 shows a diagram of the discrete-time PI current control system. The control system is composed of a plant system, a virtual synchronous generator model, and a PI controller using a dq transformation.
The system equation of the discrete-time PI controller is given below.
![]()
(38)
![]()
(39)
where ![]()
is the dq-transformed vik, and ![]()
and ![]()
are the dq-transformed ivok and, ipok.
![]()
(40)
![]()
Figure 4. PI current control with the virtual synchronous generator model.
The PI controller has the proportional gain KP and integral gain KI. The PI controller gains are obtained using a limited sensitivity method.
3.2. Transient Response
In this section, we compare the responses between the PI control and the proposed method when the output power reference is changed in steps.
In wind power generation, the wind power changes every moment according to the variable wind speed. Assuming the worst case that, the initial output power reference is 1 [pu], steps down to 0 [pu] at 4 [s], and then steps up to 1 [pu] at 5 [s].
The virtual synchronous generator has a synchronous impedance: 2.0 [pu], Mg:3.5 [s] and Tg:Mg/0.01 [s]; Kgov:1/0.05 ωbase; Kavg:0.5;![]()
:1.06; LCL filter reactance of the converter side 0.024 [pu] and of the grid side 0.044 [pu]; a loss resistor 0.001 [pu]; a cutoff frequency 10.2 ωbase; the infinite grid side impedance 0.3 [pu] (self-capacity base).
Both controllers use the same virtual synchronous generator model. When the output power reference changes, the output power oscillates according to the virtual synchronous generator model (Figure 5(b), Figure 6(b)). The inertia of the virtual synchronous generator also suppresses the slowdown of the rotor speed (Figure 5(a), Figure 6(a)).
Figure 5(d) is compared to Figure 6(d). The proposed method has only a steady vibration of less than 0.6%, however it is sufficient for following the virtual generator model. Furthermore, the conventional method has a transient fluctuation with a max peak of 25% or less.
The proposed method can output the virtual synchronous generator current more accurately.
Both control methods have almost the same active power, and can follow the virtual synchronous generator model accurately enough (Figure 5(b), Figure 6(b)). In the conventional method, the fluctuation of the reactive power is larger than that of the proposed method (Figure 5(c), Figure 6(c)), because of the following error in the current.
The internal phase angle delta in the proposed controller is within the range of 0 to 30 [deg] (Figure 5(e)). However, the internal phase angle exceeds 45 [deg] in the conventional method (Figure 6(f)). Therefore, it can be said the proposed method is more stable than the conventional method. As a result, both control methods can follow the active power of the virtual synchronous generator model accurately enough. However, conventional method has large fluctuations in the reactive power response. On the other hand, proposed method does not require additional power, so that capacity of the converter can be reduced and the stability of the virtual synchronous generator is superior to the conventional one.
4. Conclusions
We proposed a discrete time model following control for the current control of a
![]()
Figure 5. Transient response of the PI currrent controller.
virtual synchronous generator. In this paper, it was shown that a discrete-time model-following control can be derived for each sampling time interval and applied to control in actual case. The proposed method is compared with the conventional PI control method. The proposed method always follows the virtual synchronous generator model more accurately than the conventional method. As a result, the fluctuation of reactive power is suppressed, which can help downsize the capacity of the device. The fluctuation of the internal phase angle of the virtual synchronous generator model can be reduced. Therefore, the
![]()
Figure 6. Transient response of the proposed current controller.
proposed method can be expected to be more stable than the conventional method.
The contribution of the proposed method to stability of the grid system depends on performance of the virtual synchronous generator model. In the future, we will verify and improve the robustness against a grid system, and examine the effectiveness when connected to the uncertain grid system with a wind power generator.
Acknowledgements
Supported by JSPS KAKENHI Grant Number JP17K06289.