Optimal Hedging Strategies of Stock Index Futures Based on the Perspective of Information Asymmetry

Jianhua Guo

School of Economics and Management, Shaoyang University, Shaoyang, China.

DOI: 10.4236/ojapps.2020.102002                

Abstract

Based on two different risk measurement criteria, this article studied the optimal hedging strategies of stock index futures in the case of asymmetric information, and discussed the influence of insider information on the hedging effect. Through simulation analysis, it can be shown that hedging people with insider information can save hedging costs to a certain extent, which also explains the reason why investors try to obtain corporate information in actual investment activities.

Keywords

Stock Index Futures, Optimal Hedging Strategy, Information Asymmetry

1. Introduction

Information asymmetry means some investors can own insider information while others can’t. If one can acquire insider information about some enterprises, she will win a penny; thus, striving to acquire insider information becomes many investors’ investment focus; accordingly, hedging with insider information also receives attention from researchers. For example, Anna A. et al. [1] studied superhedging for contingent claims under insider information situation, in their research; Anna A. et al. considered two agents, one who only observes the stock prices and another with some additional information, and investigated when the pricing-hedging duality for the former extends to the latter. Eyraud-Loisel A. and Royer-Carenzi M. [2] studied the American option hedging by an insider by using the backward stochastic differential equations; they proved the existence and uniqueness of backward stochastic differential equations solutions, when terminal time was random, under an initially enlarged filtration. Klusik P. et al. [3] considered the problem of the quantile hedging from the point of view of a better informed agent acting on the market. Schweizer M. et al. [4] solved the problems of mean-variance hedging (MVH) and mean-variance portfolio selection (MVPS) under restricted information. Biagini and Oksendal [5] studied insider’s variance-minimizing hedging under diffusion settings. Subsequently, Biagini and Oksendal [6] also investigated the same problem with stochastic integral method. Lee K. and Song S. [7] studied locally risk-minimizing hedging problem under jump-diffusion process, in which the Poisson’s intensity is driven by insider information. Yan H.F. et al. [8] assumed that there is additional market information in the financial market and considered the mixed hedging problem. Yang et al. [9] [10] respectively studied the shortfall-risk minimizing hedging and quadratic hedging for contingent claims under insider information situation and respectively acquired hedging strategy expressions.

However, throughout the above-mentioned literatures, though research on insider’s hedging has been deeply studied and many research findings have been acquired, most are restricted to theoretical research and the optimal hedging strategy expressions comprise components hard to be measured in practical hedging.

In this paper, assuming the underlying asset price evolving as a jump-diffusion process, we aim to study the hedging strategies under asymmetric information situations and try to give an explicit solution to the optimal hedging strategy of insiders; then, we also discuss the effect of insider information to the hedging effect.

The remainder of this paper is organized as follows. In the next section, we simply introduce the market model and some definition and signs. In Section 3, we will discuss the hedging questions with different risk-measuring criteria for insiders and general hedgers and empirical analysis based on simulation method is proposed in Section 4, while discussion and conclusion in Section 5.

2. Some Preliminaries

Hypothesis: In this paper, assuming the underlying asset price evolving as a jump-diffusion process, we study hedging strategies under asymmetric information situations and discuss the effect of insider information to hedging effect.

Let $\left(\Omega ,F,P\right)$ be a complete probability space with filtration $F={\left(F_t\right)}_{t\in \left[0,T\right]}$ and the nonnegative price of risky asset $S={\left(S_t\right)}_{t\in \left[0,T\right]}$ be adapted to F, as to any stochastic sequence $s={\left(s_t\right)}_{t=0,1,\cdots ,T}$, $\Theta \left(s\right)$ denotes a sequence space consisting of respected stochastic sequence ${\left({\vartheta }_t\right)}_{t=0,1,\cdots ,T}$ with ${\vartheta }_t\Delta s_t\in L^2\left(P\right),t=0,1,\cdots ,T$.

In order to measure the asymmetry of the financial market information, in this paper, we assume that $F_T$ -measurable random variable $l_t$ denotes insider information, such as risky asset’s price or its fluctuation range, or an impulse to risky asset’s price. Thus, as for insiders, their acquired information set is enlarged information flow $G_t:=F_t\vee \sigma \left(l_t\right)$ and for insiders, the risky asset price evolves as

$\text{d}{S}_t^{\left(l\right)}=S_t^{\left(l\right)}\left[\mu \text{d}t+\sigma \text{d}{W}_t+\text{d}\left(l_t+{\displaystyle \underset{i=1}{\overset{N\left(t\right)}{\sum }}\left(V_i-1\right)}\right)\right]$ (1)

There, we assume the insider information $l_t$ obey to some certain distribution, $Y_i=\ln V_i~N\left({\mu }_J,{\sigma }_J^2\right)$ and $\left\{Y_i,i=1,2,\cdots \right\}$ is independent and identical distribution, $N\left(t\right)$ is a Poisson process with Poisson’s intensity $\lambda$.

About Equation (1), it can be solved as

$S_n^{\left(l\right)}=S_{n-1}^{\left(l\right)}\exp \left\{{\left(\mu -\frac{{\sigma }^2}{2}\right)}^2\Delta t+\sigma \sqrt{\Delta t}\epsilon +{\displaystyle \underset{i=1}{\overset{N\left(\Delta t\right)}{\sum }}{Y}_i}+l_{\Delta t}\right\}$, where $\epsilon ~N\left(0,1\right)$ is a

standard normal variable. In fact, Equation (1) also denotes the risky asset’s price process of general investors if let $l_t\equiv 0$.

Thus, we can call a 2-dimension stochastic process $\phi ={\left({\vartheta }_t,{\delta }_t\right)}_{t=0,\cdots ,T-1}$ an investment strategy, which follows as

$V_t\left(\phi \right):={\vartheta }_t{S}_t+{\delta }_t{B}_t\in L^2\left(P\right)$ (2)

where $\left({\vartheta }_t,{\delta }_t\right)$ denotes the hedging positions held at time t, and $B_t$ denotes the riskless asset’s price, which evolves as $\text{d}{B}_t=r{B}_t\text{d}t$ (where, r is riskless interest rate).

Furthermore, we call it a self-financing strategy when $\phi =\left({\vartheta }_t,{\delta }_t\right),t=0,\cdots ,T-1$ satisfies

${\vartheta }_t{S}_{t+1}+{\delta }_t{B}_{t+1}={\vartheta }_{t+1}{S}_{t+1}+{\delta }_{t+1}{B}_{t+1}$ (3)

As a matter of convenience, we equidistantly divide the hedging horizon $\left[0,T\right]$ with time step size $\Delta t=T/N$ and let $S_n^{\left(l\right)}:=S_{n\Delta t}^{\left(l\right)},n=0,1,\cdots ,N$ denote risky asset price at moment $t=n\Delta t$.

3. Hedging Strategies

3.1. Quadratic Hedging Strategies of Insider and General Hedger

Suppose an investor has initially written a share of Stock Index Future with striking price K and T horizon, in order to minimize the terminal squared error between value of hedging portfolio and contingent claim, she hedges by self-financing at discrete time $\left\{0,1,\cdots ,T-1\right\}$, thus, the hedging model is as following

$\{\begin{array}{l}\underset{\left({\phi }_0,\cdots ,{\phi }_{N-1}\right)}{\min }E{\left[V_N\left(\phi \right)-H_N\right]}^2\\ \text{s}\text{.t}\text{.}{\vartheta }_n{S}_{n+1}^{\left(l\right)}+{\delta }_n{B}_{n+1}={\vartheta }_{n+1}{S}_{n+1}^{\left(l\right)}+{\delta }_{n+1}{B}_{n+1}\\ n=0,\cdots ,N-1\end{array}$ (4)

There are $H_N={\left(S_N^{\left(l\right)}-K\right)}^{+}$, and $V_N={\vartheta }_{N-1}{S}_N^{\left(l\right)}+{\delta }_{N-1}{B}_N$.

Assume all assets’ prices are discounted. According to dynamic programming and with backward recursion method, we can solve (4) as following

At time $t=\left(N-1\right)\Delta t$, there is

$\underset{{\phi }_{N-1}}{\min }E\left[{\left(V_N-H\right)}^2|F_{N-1}\right]$

$\begin{array}{l}=\underset{{\phi }_{N-1}}{\min }E\left[{\left({\vartheta }_{N-1}{S}_N^{\left(l\right)}+{\delta }_{N-1}{B}_N-H\right)}^2|F_{N-1}\right]\\ =\underset{{\phi }_{N-1}}{\min }E\left[{\left(V_{N-1}+{\vartheta }_{N-1}\Delta S_N^{\left(l\right)}-H\right)}^2|F_{N-1}\right]\end{array}$ (5)

Denote $Z_{\Delta t}:={\left(\mu -\frac{{\sigma }^2}{2}\right)}^2\Delta t+\sigma \sqrt{\Delta t}\epsilon +{\displaystyle \underset{i=1}{\overset{N\left(\Delta t\right)}{\sum }}{Y}_i}$, then

$\Delta S_N^{\left(l\right)}=S_N^{\left(l\right)}-S_{N-1}^{\left(l\right)}=S_{N-1}^{\left(l\right)}\left({\text{e}}^{\left(Z_{\Delta t}+l\right)}-1\right)$,

and solving (5), then let

$\begin{array}{l}\frac{\partial }{\partial {\vartheta }_{N-1}}E\left[{\left(V_{N-1}+{\vartheta }_{N-1}\Delta S_N^{\left(l\right)}-H\right)}^2|F_{N-1}\right]\\ =\frac{\partial }{\partial {\vartheta }_{N-1}}E\left[{\left(V_{N-1}+{\vartheta }_{N-1}\Delta S_N^{\left(l\right)}-H\right)}^2|F_{N-1}\right]\\ =2E\left[\left(V_{N-1}+{\vartheta }_{N-1}\Delta S_N^{\left(l\right)}-H\right)\Delta S_N^{\left(l\right)}|F_{N-1}\right]\\ =0\end{array}$

There is,

$\{\begin{array}{l}{\vartheta }_{N-1}^{*}=\frac{E\left[H\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]-V_{N-1}E\left[\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]}{S_{N-1}^{\left(l\right)}E\left[{\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)}^2|F_{N-1}\right]}\\ {\delta }_{N-1}^{*}=\frac{V_{N-1}-{\vartheta }_{N-1}^{*}{S}_{N-1}^{\left(l\right)}}{B_{N-1}}\end{array}$ (6)

and

$\begin{array}{c}J\left(N-1,V_{N-1}\right):=\underset{{\phi }_{N-1}}{\min }E\left[{\left(V_N-H\right)}^2|F_{N-1}\right]\\ ={\left(V_{N-1}-H_{N-1}\right)}^2+E\left[{\left(H-{\vartheta }_{N-1}^{*}\Delta S_N^{\left(l\right)}\right)}^2|F_{N-1}\right]\\ -E^2\left[{\left(H-{\vartheta }_{N-1}^{*}\Delta S_N^{\left(l\right)}\right)}^2|F_{N-1}\right]\end{array}$ (7)

Substituting (6) into (7), there is

$\begin{array}{l}J\left(N-1,V_{N-1}\right)\\ =V_{N-1}^2\left\{1-\frac{E^2\left[\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]}{E\left[{\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)}^2|F_{N-1}\right]}\right\}\\ -2V_{N-1}\left\{E\left(H|F_{N-1}\right)-\frac{E\left[H\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]E\left[\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]}{E\left[{\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)}^2|F_{N-1}\right]}\right\}\\ +E\left(H^2|F_{N-1}\right)-\frac{E^2\left[H\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]}{E\left[{\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)}^2|F_{N-1}\right]}\\ =a_{N-1}{V}_{N-1}^2-2b_{N-1}{V}_{N-1}+c_{N-1}\end{array}$

where, there are

$a_{N-1}=1-\frac{E^2\left[\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]}{E\left[{\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)}^2|F_{N-1}\right]}$

$b_{N-1}=E\left(H|F_{N-1}\right)-\frac{E\left[H\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]E\left[\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]}{E\left[{\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)}^2|F_{N-1}\right]}$

$c_{N-1}=E\left(H^2|F_{N-1}\right)-\frac{E^2\left[H\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)|F_{N-1}\right]}{E\left[{\left({\text{e}}^{\left(Z_{\Delta t}+l_{\Delta t}\right)}-1\right)}^2|F_{N-1}\right]}$

Just as acquiring $\left({\vartheta }_{N-1}^{*},{\delta }_{N-1}^{*}\right)$, with constraint of self financing, at $t=n\Delta t,n=N-2,\cdots ,0$, there are

$\{\begin{array}{l}{\vartheta }_n^{*}=\frac{E\left[b_{n+1}\left({\text{e}}^{Z_{\Delta t}}-1\right)|F_n\right]-V_{n}E\left[a_{n+1}\left({\text{e}}^{Z_{\Delta t}}-1\right)|F_n\right]}{S_n^{\left(l\right)}E\left[a_{n+1}{\left({\text{e}}^{Z_{\Delta t}}-1\right)}^2|F_n\right]}\\ {\delta }_n^{*}=\frac{V_n-{\vartheta }_n^{*}{S}_n^{\left(l\right)}}{B_n}\end{array}$ (8)

where, there are

$a_n=E\left(a_{n+1}|F_n\right)-\frac{E^2\left[a_{n+1}\left({\text{e}}^{Z_{\Delta t}}-1\right)|F_n\right]}{E\left[a_{n+1}{\left({\text{e}}^{Z_{\Delta t}}-1\right)}^2|F_n\right]}$

$b_n=E\left(b_{n+1}|F_n\right)-\frac{E\left[a_{n+1}\left({\text{e}}^{Z_{\Delta t}}-1\right)|F_n\right]E\left[b_{n+1}\left({\text{e}}^{Z_{\Delta t}}-1\right)|F_n\right]}{E\left[a_{n+1}{\left({\text{e}}^{Z_{\Delta t}}-1\right)}^2|F_n\right]}$

$c_n=E\left(c_{n+1}|F_n\right)-\frac{E^2\left[b_{n+1}\left({\text{e}}^{Z_{\Delta t}}-1\right)|F_n\right]}{E\left[a_{n+1}{\left({\text{e}}^{Z_{\Delta t}}-1\right)}^2|F_n\right]}$

$V_n=V_0+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\vartheta }_{i-1}^{*}\Delta S_i^{\left(l\right)}}=\frac{b_0}{a_0}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\vartheta }_{i-1}^{*}\Delta S_i^{(l)}}$

In fact, if let $l\equiv 0$, then, (8) denote the quadratic hedging strategy of general hedger.

3.2. Risk Minimizing Hedging Strategies of Insider and General Hedger

The quadratic hedging are restricted with self-financing, in this subsection, we relax self-financing constraint and study risk-minimizing hedging problem, which try to minimize the terminal squared error with following optimizing model (9)

$\{\begin{array}{l}\underset{\left({\delta }_n,{\theta }_n\right)}{\min }E\left[{\left(C_N\left(\phi \right)-C_n\left(\phi \right)\right)}^2|F_n\right]\\ \text{s}\text{.t}.V_N\left(\phi \right)=H={\left(S_N^{\left(l\right)}-K\right)}^{+}\\ n=0,1,\cdots ,N-1\end{array}$ (9)

In (10), $C_N\left(\phi \right)-C_n\left(\phi \right)$ denotes the future cost increment of strategy $\phi$

and $\underset{\left(\phi \right)}{\min }E\left[{\left(C_N\left(\phi \right)-C_n\left(\phi \right)\right)}^2|F_n\right]$ substantially minimizes the conditional

variance of the cost increment. Just as before, with discounted asset prices and with constraint of $V_N\left(\phi \right)=H$, there is

(10)

In fact, the cost process of risk-minimizing hedging is a martingale. Thus, the optimal hedging strategy for (10) may be acquired by solving (11) as below

(11)

In fact, because, there is

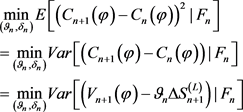(12)

where, there is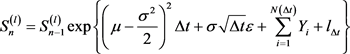, and denoting

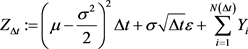, then,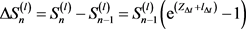

At time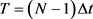, i.e., 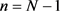, under the constraint of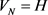, we can solve (12) and there is

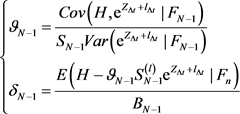(13)

Next, making use of the martingale character of hedging cost process with risk minimizing optimizing object, at, we can recursively solve (12) and there are

(14)

In fact, if let, (14) denotes the quadratic hedging strategy of general hedger.

4. Numerical Example

In this section, taking example for hedging for Stock Index Future with 3-month maturity, we compare and analyze the hedging effect of insiders and general hedgers. Let underlying asset’s initial price, striking price of Stock Index Future, , 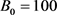and riskless interest rate, parameters of jump-diffusion process as, , , ,.

Furthermore, we respectively assume the insider information and with, and.

As to two different hedgers, we denote

Strategy Outsider: general hedger who hedges respectively according to (8) sand (14) with.

Strategy Insider: insider who hedges respectively according to (8) and (14).

Then, we can respectively calculate the total hedging costs and total hedging error for insider and general hedger just following (15) and (16)

(15)

There, , denoting the transaction commission rate of riskless asset.

(16)

Table 1 and Table 2 respectively show the total hedging cost and total hedging error of insider and general hedger with quadratic hedging criteria, when Table 3 shows the total hedging cost of insider and general hedger with risk-minimizing hedging criteria, because of the constraint of, the hedging error of both insider and general hedger with risk-minimizing hedging criteria equal to zero.

From Tables 1-3, we can see that, insiders can not only save hedging costs, but also reduce hedging losses. For example, under quadratic hedging criteria, inside information hedgers can respectively save hedging costs by 0.21% - 0.7% and reduce hedging error by 1.29% - 1.67% under quadratic hedging criteria (seen in Table 1 and Table 2). Under risk-minimizing hedging criteria, the hedging error is zero for both insiders and ordinary hedgers, but inside information hedgers can save hedging costs by 0.46% - 1.17%.

Table 1. Total hedging cost of insider and general hedger (quadratic hedging criteria).

Table 2. Total hedging error of insider and general hedger (quadratic hedging criteria).

Table 3. Total hedging cost of insider and general hedger (risk-minimizing hedging criteria).

5. Conclusions

In this paper, we studied the hedging problems with two different risk-measuring criteria for insiders and general hedgers. First, based on the analysis of insider market information, we construct a jump-diffusion model to depict risky asset price process, then, in virtue of dynamic programming, and backward recursive method, we solve hedging problems for insiders and analyze the influence of inside information on hedging effect.

Table 1 and Table 3 indicate that insiders can save hedging cost to a certain extent for owning some insider information than those investors who are outsiders. From Table 1 and Table 3, we can detect that, for quadratic hedging and risk-minimizing hedging, insiders can save hedging cost about 0.21% - 1.17% than outsiders. At the same time, we can also see from Table 2 that the total hedging error of insider with risk-minimizing hedging criteria is small than that of general hedger. By this token, whether owning additional insider information is a crucial factor for investors to succeed or not, which is one reason why many people strive to defraud enterprise information.

So, to supervisory board, to reinforce insider information management is a necessary and important method to ensure fair transaction and domestic financial market’s healthy development. For example, the legislative branch can restrict the leakage of inside information and prevent insider trading through legislation. Law enforcement or regulatory authorities may impose corresponding penalties on insider traders. For traders, they must consciously abide by the rules of the transaction and jointly maintain the fairness of the transaction.

All in all, this paper studied the hedging problem under the condition of asymmetric information, and gave the analytical formula of the optimal hedging strategy under the square hedging criterion and the risk minimization hedging criterion for inside information hedgers and general hedgers. However, because the minimum loss hedging criterion is non-differentiable, the limitation of this research is that this article has not conducted research on the optimal hedging strategy under the minimum loss criterion, which is also one of our future research directions.

Acknowledgements

The study was supported by the Hunan provincial social science fund project of China (Project Number: 17YBA354).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Aksamit, A., Hou, Z. and Obl’Oj, J. (2016) Robust Framework for Quantifying the Value of Information in Pricing and Hedging. SIAM Journal on Financial Mathematics, 11, 27-59. https://doi.org/10.1137/18M1177597
[2]	Eyraud-Loisel, A. and Royer-Carenzi, M. (2010) BSDEs with Random Terminal Time under Enlarged Filtration. American-Style Options Hedging by an Insider. Random Operators and Stochastic Equations, 18, 141-163. https://doi.org/10.1515/rose.2010.008
[3]	Klusik, P., Palmowski, Z. and Zwierz, J. (2008) Quantile Hedging for an Insider. Probability and Mathematical Statistics, 30, 247-258.
[4]	Schweizer, M., Zivoi, D. and Sikic, M. (2018) Dynamic Mean-Variance Optimization Problems with Deterministic Information. International Journal of Theoretical and Applied Finance, 21, Article ID: 1850011. https://doi.org/10.1142/S0219024918500115
[5]	Biagini, F. and Oksendal, B. (2004) Minimal Variance Hedging for Insider Trading. Pure Mathematics, No. 9, 1-23.
[6]	Biagini, F. and Oksendal, B. (2006) Minimal Variance Hedging for Insider Trading. International Journal of Theoretical and Applied Finance, 9, 1351-1375. https://doi.org/10.1142/S0219024906003998
[7]	Lee, K. and Song, S. (2007) Insiders’ Hedging in a Jump Diffusion Model. Quantitative Finance, 7, 537-545. https://doi.org/10.1080/14697680601043191
[8]	Yan, H., Yang, J. and Liu, L. (2008) Mixed Hedging under Additive Market Price Information. Journal of Systems Science and Complexity, No. 2, 84-94. https://doi.org/10.1007/s11424-008-9107-9
[9]	Yang, J. and Xiao, Q. (2010) Risk-Minimizing Hedging Strategies with Restricted Information and Cost. Applied Stochastic Models in Business & Industry, 26, 401-415. https://doi.org/10.1002/asmb.794
[10]	Yang, J. and Xiao, Q. (2011) Quadratic Hedging Strategies under Inner Information. Chinese Journal of Applied Probability & Statistics, 27, 297-304.