How to Explicitly Calculate Feynman and Wheeler Propagators in the ADS/CFT Correspondence

Angelo Plastino^1,2,3*, Mario C. Rocca^1,2,4

¹Departamento de Física, Universidad Nacional de La Plata, La Plata, Argentina.
²Consejo Nacional de Investigaciones Científicas y Tecnológicas (IFLP-CCT-CONICET)-C. C. 727, La Plata, Argentina.
³SThAR-EPFL, Lausanne, Switzerland.
⁴Departamento de Matemática, Universidad Nacional de La Plata, La Plata, Argentina.

DOI: 10.4236/jmp.2020.112019                

Abstract

We discuss, giving all necessary details, the boundary-bulk propagators. We do it for a scalar field, with and without mass, for both the Feynman and the Wheeler cases. Contrary to standard procedure, we do not need here to appeal to any unfounded conjecture (as done by other authors). Emphasize that we do not try to modify standard ADS/CFT procedures, but use them to evaluate the corresponding Feynman and Wheeler propagators. Our present calculations are original in the sense of being the first ones undertaken explicitly using distributions theory (DT). They are carried out in two instances: 1) when the boundary is a Euclidean space and 2) when it is of Minkowskian nature. In this last case we compute also three propagators: Feynman’s, Anti-Feynman’s, and Wheeler’s (half advanced plus half retarded). For an operator corresponding to a scalar field we explicitly obtain, for the first time ever, the two points’ correlations functions in the three instances above mentioned. To repeat, it is not our intention here to improve on ADS/CFT theory but only to employ it for evaluating the corresponding Wheeler’s propagators.

Keywords

ADS/CFT Correspondence, Boundary-Bulk Propagators, Feynman’s Propagators, Wheeler’s Propagators

1. Introduction

Propagators and correlators are one of the essential tools to work, for example, in Quantum Field Theory (QFT) and String Theory (ST), in particular, in formulating the correspondence ADS/CFT (Anti-de Sitter/Conformal Field Theory). This correspondence was established by Maldacena [1] in 1998 and is universally regarded as a very useful model for many purposes.

The bibliography on this subject, for scalar fields, is quite extensive. We give here just a small representative in [2] - [12]. For a more complete bibliography the reader is directed to the report [13].

One of the ADS/CFT correspondence’s prescriptions (see [2]) will allow us to evaluate the correlators on the boundary of ADS space. The first boundary-bulk propagator was calculated by Witten a few months after the appearance of [1], entitled Anti de Sitter space and holography. In this case the boundary is a Euclidean space [2] [3].

In this work, instead, we evaluate the boundary-bulk propagators for the case in which the boundary is a Minkowskian space. In such regards, remark that some attempts have been made before in [14] [15] [16].

1.1. The Wheeler Propagator

The Feynman’s propagator for a free real scalar field is a time-ordered correlation function of two scalar fields $\Phi \left(x\right)$ and $\Phi \left(y\right)$ in the vacuum state

$G_F\left(x-y\right)=\langle 0|\hat{T}\Phi \left(x\right)\Phi \left(y\right)|0\rangle \mathrm{.}$ (1.1)

This propagator is a Green function of the Klein-Gordon equation, and is discussed in almost any text-book on quantum mechanics. Not so well-known at all is the Wheeler propagator. In fact, to provide a fairly complete description of it constitutes one of the present goals.

More than half a century ago, J. A. Wheeler and R. P. Feynman published a work [17] in which they represented electromagnetic interactions by means of a half advanced and half retarded Green functions. The charged medium was supposed to be a perfect absorber, so that no radiation could possibly escape the system.

We are going to call this kind of Green function a “Wheeler function’’ (or propagator). It has been used before by P. A. M. Dirac [18], when trying to avoid some run-away solutions, in which one finds rapid increases that cannot be controlled. Later on, in 1949, J. A. Wheeler and R. P. Feynman showed that, in spite of the fact that the Green function contains an advanced part, the results do no contradict causality [19].

A causal, unitary, and Lorentz invariant quantification of tachyons was performed in reference [20]. The corresponding propagator is precisely a Wheeler’s one.

The same happens with complex mass particles that appear in higher order supersymmetric models [21]. For these particles, the propagator is also a Wheeler’s propagator.

We review some precedent work below.

1.2. The Starinets and Son Paper

The main previous attempt to try to calculate boundary-bulk propagators in the Minkowskian boundary for the Anti-de Sitter space [in the ADS/CFT correspondence] was made by Son and Starinets (SS) in 2002 [22]. However, SS needed to formulate a conjecture that we show here to become unnecessary if one uses the full distributions-theory of type S’ (of Schwartz). SS literally state (the necessary symbols will be explained later in the text) “We circumvent the difficulties mentioned above by putting forward the following conjecture

$G^R\left(k\right)={-2F\left(k\mathrm{,}z\right)|}_{z_B}$ (3.15)”

For this conjecture no rigorous mathematical basis is presented. Instead, we will nor need here any conjecture at all. SS’ work was entitled “Minkowski-space correlators in AdS/CFT correspondence: recipe and applications”.

1.3. The Freedman et al. Paper

We must also mention the work of Freedman et al. [23], in which the authors deal with the case of a Euclidean boundary. Freedman, however, did not treat the case of a Minkowskian boundary, at least in the way that Son and Starinets did. To repeat, we make full use here of distribution theory. This does not entail, of course, a simple $iϵ$ prescription, but a much more elaborate treatment, that has not been performed before in this field. Let us also remark, as this is an important point for us, that in this paper we do not evaluate renormalized correlation functions.

1.4. Our Treatment

As stated above, in the present effort we evaluate, without any a la Starinets and Son conjecture, the boundary-bulk propagators corresponding to the following three cases i) Feynman, ii) Anti-Feynman, and iii) Wheeler (half advanced plus half retarded). We do this both for massless and massive scenarios (a scalar field involved). Later we calculate the two points correlators (TPC) for operators corresponding to this scalar field in the three instances previously mentioned. We clarify that in this paper we do not evaluate the renormalized TPC.

We demonstrate as well that the Feynman propagator must be a function of $\rho +i0$ (see below for the notation) in momentum space, and therefore a function of $x^2-i0$ in configuration space. We show that something similar happens with the Anti-Feynman propagator. For the first time ever, we calculate the Wheeler’s propagator (half advanced plus half retarded) as well.

As usual, we use here regularity conditions 1) at the origin (Dirichlet’s) and 2) of rapid decay at infinity (boundary condition). This applies, for instance, to Equations (2.8), (2.9), and (2.10).

It may be asserted that propagators are always to be interpreted in a distributional sense, but most authors do not employ, in dealing with them, the FULL distribution theory developed by Laurent Schwartz [24] and Israelovich M. Guelfand et al. [25].

Note also that, until the 90’s, the only field propagators that had been calculated were Anti-de Sitter (spatial) ones.

1.5. Organization of This Work

The paper is organized as follows: Section 2 deals with the Euclidean case. In it, the three different propagators referred to above cannot be distinguished (neither in the massive nor in the massless instances).

In Section 3, we tackle similar scenarios as those of Section 2, but now in Minkowski’s space, where the three propagators can be distinguished.

In Section 4, we compute in Euclidean space the TPC for a scalar operator corresponding to a scalar field via Witten’s prescription.

In Section 5, we generalize the calculations of Section 4 to Minkowski’s space. We obtain in this fashion the two-point correlations functions corresponding to the three different propagators of our list above.

Finally, some conclusions are drawn in Section 6.

2. Euclidean Case

2.1. Massless Scalar Field Propagator

The Klein-Gordon equation in $AD{S}_{\nu +1}$ for the scalar field $\varphi \left(z\mathrm{,}x\right)$ reads, in Poincare coordinates,

$z^2{\partial }_z^2\varphi \left(z\mathrm{,}x\right)+\left(1-\nu \right)z{\partial }_z\varphi \left(z\mathrm{,}x\right)+z^2{\nabla }^2\varphi \left(z\mathrm{,}x\right)-\Delta \left(\Delta -\nu \right)\varphi \left(z\mathrm{,}x\right)=\mathrm{0,}$ (2.1)

where $\Delta \left(\Delta -\nu \right)\ge 0$ plays the role of $m^2$. We exclude tachyons form of this treatment. Here $\Delta$ is the conformal dimension, $\nu$ the boundary’s dimension, and $x$ their coordinates. The Fourier transform in the variables $x$ of the field $\varphi \left(z\mathrm{,}x\right)$ is

$\hat{\varphi }\left(z\mathrm{,}k\right)={\displaystyle \int }\varphi \left(z\mathrm{,}x\right){\text{e}}^{ik\cdot x}{\text{d}}^{\nu }x\mathrm{.}$ (2.2)

Using (2.2), (2.1) takes the form

$z^2{\partial }_z^2\hat{\varphi }\left(z\mathrm{,}k\right)+\left(1-\nu \right)z{\partial }_z\hat{\varphi }\left(z\mathrm{,}k\right)-\left[z^2{k}^2+\Delta \left(\Delta -\nu \right)\right]\hat{\varphi }\left(z\mathrm{,}k\right)=0.$ (2.3)

We analyze now the massless case given by $\Delta =0,\nu$. For it we have the motion equation

$z^2{\partial }_z^2\hat{\varphi }\left(z\mathrm{,}k\right)+\left(1-\nu \right)z{\partial }_z\hat{\varphi }\left(z\mathrm{,}k\right)-z^2{k}^2\hat{\varphi }\left(z\mathrm{,}k\right)=\mathrm{0,}$ (2.4)

or equivalently (for $z\ne 0$ ),

${\partial }_z^2\hat{\varphi }\left(z\mathrm{,}k\right)+\frac{1-\nu }{z}{\partial }_z\hat{\varphi }\left(z\mathrm{,}k\right)-k^2\hat{\varphi }\left(z\mathrm{,}k\right)=0.$ (2.5)

In the variable z, this equation is of the Bessel type (see [26])

$F^{″}\left(z\right)+\frac{1-2\alpha }{z}{F}^{\prime }\left(z\right)-\left[k^2+\frac{{\mu }^2-{\alpha }^2}{z^2}\right]F\left(z\right)=0$ (2.6)

The pertinent solution (that does not diverge when the argument tends to infinity) is

$F\left(z\right)=z^{\alpha }{\mathcal{K}}_{\mu }\left(kz\right)\mathrm{.}$ (2.7)

Thus, the solution of (2.5) becomes

$\hat{\varphi }\left(z\mathrm{,}k\right)=z^{\frac{\nu }{2}}{\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right)\mathrm{.}$ (2.8)

One easily verifies that, for infinitesimal z [26],

${\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right)=\frac{2^{\frac{\nu }{2}-1}\Gamma \left(\frac{\nu }{2}\right)}{{\left(kz\right)}^{\frac{\nu }{2}}}+O\left({\left(kz\right)}^{-\frac{\nu }{2}+2}\right)\mathrm{.}$ (2.9)

Equation (2.9) is just a Bessel-McDonald distribution (defined by Guelfand [25]) in Euclidean space. As a consequence,

$\underset{z\to 0}{\lim }{z}^{\frac{\nu }{2}}{\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right)=\frac{2^{\frac{\nu }{2}-1}\Gamma \left(\frac{\nu }{2}\right)}{k^{\frac{\nu }{2}}}\mathrm{.}$ (2.10)

In other words, the solution is regular at the origin and vanishes at infinity (in the variable z). Accordingly, we have, for the field in the bulk, the solution

$\varphi \left(z\mathrm{,}x\right)=\frac{z^{\frac{\nu }{2}}}{{\left(2\pi \right)}^{\nu }}{\displaystyle \int }a\left(k\right){\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k\mathrm{.}$ (2.11)

This solution must reduce itself to the field ${\varphi }_0\left(x\right)$ on the boundary, so that

$\varphi \left(0,x\right)={\varphi }_0\left(x\right)=\frac{2^{\frac{\nu }{2}-1}\Gamma \left(\frac{\nu }{2}\right)}{{\left(2\pi \right)}^{\nu }}{\displaystyle \int }a\left(k\right)k^{-\frac{\nu }{2}}{\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k=\frac{1}{{\left(2\pi \right)}^{\nu }}{\displaystyle \int }{\hat{\varphi }}_0\left(k\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k.$ (2.12)

From this last equation we can obtain $a\left(k\right)$ as a function of ${\hat{\varphi }}_0$ and then write

$\varphi \left(z\mathrm{,}x\right)=\frac{z^{\frac{\nu }{2}}{2}^{1-\frac{\nu }{2}}}{{\left(2\pi \right)}^{\nu }\Gamma \left(\frac{\nu }{2}\right)}{\displaystyle \int }{k}^{\frac{\nu }{2}}{\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right){\hat{\varphi }}_0\left(k\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k,$ (2.13)

or, equivalently,

$\varphi \left(z\mathrm{,}x\right)=\frac{z^{\frac{\nu }{2}}{2}^{1-\frac{\nu }{2}}}{{\left(2\pi \right)}^{\nu }\Gamma \left(\frac{\nu }{2}\right)}{\displaystyle \iint }{k}^{\frac{\nu }{2}}{\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right){\varphi }_0\left(x^{\prime }\right){\text{e}}^{-ik\cdot \left(x-x^{\prime }\right)}{\text{d}}^{\nu }k{\text{d}}^{\nu }{x}^{\prime }.$ (2.14)

From (2.14) we then obtain an expression of the boundary-bulk propagator

$K\left(z\mathrm{,}x-x^{\prime }\right)=\frac{z^{\frac{\nu }{2}}{2}^{1-\frac{\nu }{2}}}{{\left(2\pi \right)}^{\nu }\Gamma \left(\frac{\nu }{2}\right)}{\displaystyle \int }{k}^{\frac{\nu }{2}}{\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right){\text{e}}^{-ik\cdot \left(x-x^{\prime }\right)}{\text{d}}^{\nu }k\mathrm{.}$ (2.15)

To carry out the integration in the variable k we appeal to the expressions for the Fourier transform and its inverse obtained by Bochner [27]. For the Fourier transform we have

$\hat{f}\left(k\right)={\displaystyle \int }f\left(x\right){\text{e}}^{ik\cdot x}{\text{d}}^{\nu }x=\frac{{\left(2\pi \right)}^{\frac{\nu }{2}}}{k^{\frac{\nu }{2}-1}}{\displaystyle \underset{0}{\overset{\infty }{\int }}}{r}^{\frac{\nu }{2}}{\mathcal{J}}_{\frac{\nu }{2}-1}\left(kr\right)f\left(r\right)\text{d}r\mathrm{,}$ (2.16)

and for its inverse

$f\left(r\right)=\frac{1}{{\left(2\pi \right)}^{\nu }}{\displaystyle \int }\hat{f}\left(k\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k=\frac{1}{{\left(2\pi \right)}^{\frac{\nu }{2}}{r}^{\frac{\nu }{2}-1}}{\displaystyle \underset{0}{\overset{\infty }{\int }}}{k}^{\frac{\nu }{2}}{\mathcal{J}}_{\frac{\nu }{2}-1}\left(kr\right)\hat{f}\left(k\right)\text{d}k.$ (2.17)

Using these relations we have now

$K\left(z,x-x^{\prime }\right)=\frac{z^{\frac{\nu }{2}}{2}^{1-\frac{\nu }{2}}}{{\left(2\pi \right)}^{\nu }\Gamma \left(\frac{\nu }{2}\right)}\frac{{\left(2\pi \right)}^{\frac{\nu }{2}}}{{\left|x-x^{\prime }\right|}^{\frac{\nu }{2}-1}}{\displaystyle \underset{0}{\overset{\infty }{\int }}}{k}^{\nu }{\mathcal{K}}_{\frac{\nu }{2}}\left(kz\right){\mathcal{J}}_{\frac{\nu }{2}-1}\left(k\left|x-x^{\prime }\right|\right)\text{d}k.$ (2.18)

So as to evaluate the last integral we appeal to a result from [26]

${\displaystyle \underset{0}{\overset{\infty }{\int }}}{x}^{\mu +\nu +1}{\mathcal{K}}_{\nu }\left(bx\right){\mathcal{J}}_{\mu }\left(ax\right)\text{d}x=2^{\mu +\nu }{a}^{\mu }{b}^{\nu }\frac{\Gamma \left(\mu +\nu +1\right)}{{\left(a^2+b^2\right)}^{\mu +\nu +1}}\mathrm{,}$ (2.19)

Our deduction follows a different, simpler and complete path than that of [2]. Our approach also has a didactic utility.

$K\left(z\mathrm{,}x-x^{\prime }\right)=\frac{\Gamma \left(\nu \right)}{{\pi }^{\frac{\nu }{2}}\Gamma \left(\frac{\nu }{2}\right)}{\left[\frac{z}{z^2+{\left(x-x^{\prime }\right)}^2}\right]}^{\nu }\mathrm{,}$ (2.20)

which leads to

$\varphi \left(z\mathrm{,}x\right)={\displaystyle \int }K\left(z\mathrm{,}x-x^{\prime }\right){\varphi }_0\left(x^{\prime }\right){\text{d}}^{\nu }{x}^{\prime }\mathrm{,}$ (2.21)

an expression that, in turn, leads to

$\underset{z\to 0}{\lim }K\left(z\mathrm{,}x-x^{\prime }\right)=\delta \left(x-x^{\prime }\right)\mathrm{.}$ (2.22)

2.2. Massive Field Propagator

We now consider the massive case $\Delta \ne \mathrm{0,}\nu$. The equation of motion for this case reads

$z^2{\partial }_z^2\hat{\varphi }\left(z\mathrm{,}k\right)+\left(1-\nu \right)z{\partial }_z\hat{\varphi }\left(z\mathrm{,}k\right)-\left[z^2{k}^2+\Delta \left(\Delta -\nu \right)\right]\hat{\varphi }\left(z\mathrm{,}k\right)=\mathrm{0,}$ (2.23)

or equivalently,

${\partial }_z^2\hat{\varphi }\left(z\mathrm{,}k\right)+\frac{1-\nu }{z}{\partial }_z\hat{\varphi }\left(z\mathrm{,}k\right)-\left[k^2+\frac{\Delta \left(\Delta -\nu \right)}{z^2}\right]\hat{\varphi }\left(z\mathrm{,}k\right)=0.$ (2.24)

The solution for this last equation is

$\hat{\varphi }\left(z\mathrm{,}k\right)=z^{\frac{\nu }{2}}{\mathcal{K}}_{\mu }\left(kz\right)\mathrm{,}$ (2.25)

with

$\mu =\pm \sqrt{\frac{{\nu }^2}{4}+\Delta \left(\Delta -\nu \right)}\mathrm{.}$ (2.26)

Since ${\mathcal{K}}_{\mu }\left(z\right)={\mathcal{K}}_{-\mu }\left(z\right)$, we select for $\mu$ in (2.26) the plus sign. We have then

$\varphi \left(z\mathrm{,}x\right)=\frac{z^{\frac{\nu }{2}}}{{\left(2\pi \right)}^{\nu }}{\displaystyle \int }a\left(k\right){\mathcal{K}}_{\mu }\left(kz\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k.$ (2.27)

For $\Delta \ne 0$, this solution is not regular at the origin. To overcome this problem we select

$\varphi \left(ϵ,x\right)={\varphi }_{ϵ}\left(x\right)=\frac{{ϵ}^{\frac{\nu }{2}}}{{\left(2\pi \right)}^{\nu }}{\displaystyle \int }a\left(k\right){\mathcal{K}}_{\mu }\left(kϵ\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k=\frac{1}{{\left(2\pi \right)}^{\nu }}{\displaystyle \int }{\hat{\varphi }}_{ϵ}\left(k\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k,$ (2.28)

where $ϵ$ is infinitesimal. From (2.28) we have then

$a\left(k\right)=\frac{{\hat{\varphi }}_{ϵ}\left(k\right)}{{ϵ}^{\frac{\nu }{2}}{\mathcal{K}}_{\mu }\left(kϵ\right)}\mathrm{.}$ (2.29)

Replacing the result of (2.29) into (2.27) we obtain

$\varphi \left(z\mathrm{,}x\right)=\frac{1}{{\left(2\pi \right)}^{\nu }}{\left(\frac{z}{ϵ}\right)}^{\frac{\nu }{2}}{\displaystyle \int }\frac{{\mathcal{K}}_{\mu }\left(kz\right)}{{\mathcal{K}}_{\mu }\left(kϵ\right)}{\hat{\varphi }}_{ϵ}\left(k\right){\text{e}}^{-ik\cdot x}{\text{d}}^{\nu }k,$ (2.30)

or similarly,

$\varphi \left(z\mathrm{,}x\right)=\frac{1}{{\left(2\pi \right)}^{\nu }}{\left(\frac{z}{ϵ}\right)}^{\frac{\nu }{2}}{\displaystyle \int }{\displaystyle \int }\frac{{\mathcal{K}}_{\mu }\left(kz\right)}{{\mathcal{K}}_{\mu }\left(kϵ\right)}{\varphi }_{ϵ}\left(x^{\prime }\right){\text{e}}^{-ik\cdot \left(x-x^{\prime }\right)}{\text{d}}^{\nu }k{\text{d}}^{\nu }{x}^{\prime }.$ (2.31)

From this last equation we see that the propagator is

$K_m\left(z,x-x^{\prime }\right)=\frac{1}{{\left(2\pi \right)}^{\nu }}{\left(\frac{z}{ϵ}\right)}^{\frac{\nu }{2}}{\displaystyle \int }\frac{{\mathcal{K}}_{\mu }\left(kz\right)}{{\mathcal{K}}_{\mu }\left(kϵ\right)}{\text{e}}^{-ik\cdot \left(x-x^{\prime }\right)}{\text{d}}^{\nu }k.$ (2.32)

As a consequence we can write

$\varphi \left(z\mathrm{,}x\right)={\displaystyle \int }{K}_m\left(z\mathrm{,}x-x^{\prime }\right){\varphi }_{ϵ}\left(x^{\prime }\right){\text{d}}^{\nu }{x}^{\prime }\mathrm{.}$ (2.33)

From (2.33) we immediately gather that

$K_m\left(ϵ\mathrm{,}x-x^{\prime }\right)=\delta \left(x-x^{\prime }\right)\mathrm{.}$ (2.34)

2.3. Wrong but Popular Approach for Approximate Massive Field Propagators

It is instructive to discuss here a popular but non-valid approach for the function. The issue here is that, although is infinitesimal, it cannot adopt a 0-value. As k is an unbounded variable, when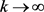, we have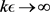. Notice first that

(2.35)

Some people make now the approximation

(2.36)

From (2.32) one obtains an approximation for the propagator K that can be called M. Ome has then

(2.37)

Using again the Bochner formula one arrives at

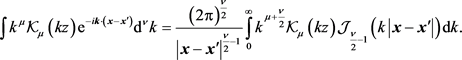(2.38)

By recourse to (2.19) it follows that

(2.39)

Defining

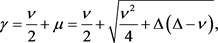(2.40)

one can write

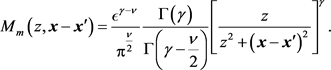(2.41)

It is then realized that, by construction,

(2.42)

and define

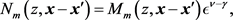(2.43)

which allows one to write for 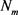the expression

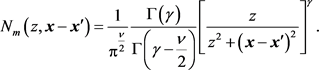(2.44)

Therefore, one has constructively proved that

(2.45)

Note that (2.44) is indeed the well known expression for the boundary-bulk propagator for a scalar field in configuration space. However, this expression can

only be used as an approximation to the propagator K when.

The above recounted approximation, not very well founded, is precisely the one most people use in current literature to obtain the propagator (2.32). From it, people deduce the approximation (2.44).

Indeed, one of the main goals of our paper is to overcome the problems posed by this approximation. We will try below to do better than current usage, and shall indeed achieve our goal.

3. Minkowskian Case

3.1. Massless Field Propagator

Let us now deal with the case in which the boundary of the 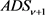is the -dimensional Minkowskian space. In the massless case the field-equation is

(3.1)

where. Thus, we can write

(3.2)

or, rewriting this last equation,

(3.3)

The distribution is defined as (see reference [24])

(3.4)

and can be cast in terms of, the Heaviside step function [24]. We recast now (3.3) in the form of a Bessel equation

(3.5)

The solution of this equation that is 1) regular at the origin and 2) vanishes for, becoming

(3.6)

One must take into account that (see below in this section and [25]).

(3.7)

Equation (3.7) is just a Bessel-McDonald distribution (defined by Guelfand [24]) in Minkowskian space. We have then

(3.8)

From this last equation we deduce that

(3.9)

or, equivalently,

(3.10)

The ensuing propagator becomes then

(3.11)

Thus, the corresponding Feynman’s propagator is

(3.12)

Note that the Feynman propagator is a function of, as it should. For the anti-Feynman propagator we have instead

(3.13)

The expression for the Wheeler’s propagator (half advanced plus half retarded) is:

(3.14)

Using the relations

(3.15)

and

(3.16)

we can define, as usual, the retarded propagator

(3.17)

and the advanced propagator

(3.18)

We are going to show now that (see [28]). Let be a test function belonging to a sub-space of Schwartz’s one [24] [25]. Its Fourier transform is

(3.19)

where belongs to. Then one can verify that

(3.20)

As a consequence, we obtain

(3.21)

(3.21) is an extremely well-known fact established by Distribution Theory, and can be found in the text-book by Jones [28]. The Feynman propagator is, according to (3.12),

(3.22)

Since is exponentially decreasing or oscillating, we can evaluate the integral that defines by means of a Wick rotation over. Therefore we have the change of variables, , , and. Casting the integral that defines the propagator in terms of these new variables, we obtain

(3.23)

Using Bochner’s formula together with (3.19) we have

(3.24)

Now, making the change to Minkowskian variables and taking into account that the Fourier transform of a distribution that depends on is a distribution that depends on, we obtain

(3.25)

which is the expression of the Feynman propagator in terms of the variables of the configuration space. For the anti-Feynman propagator we analogously find

(3.26)

3.2. Massive Field Propagator

For the massive case, the field-motion equation is

(3.27)

with, again,

(3.28)

The pertinent solution is now

(3.29)

The field-expression in configuration space is then

(3.30)

Once again we choose

(3.31)

and from (3.23) we obtain

(3.32)

We have then the following relation for the solution

(3.33)

so that the propagator is now

(3.34)

The corresponding Feynman’s propagator becomes

(3.35)

For the anti-Feynman propagator we obtain the expression

(3.36)

Finally, the definition of Wheeler propagators, half retarded and half advanced, is similar to that of the preceding subsection, this is:

(3.37)

3.3. An Approximation

We now evaluate in approximate fashion the propagator

(3.38)

entailing

(3.39)

Effecting again the above Wick’s rotation we obtain

(3.40)

This integral is evaluated as in the previous cases. One has

(3.41)

Changing variables as above we arrive at

(3.42)

where

(3.43)

Now we return to the inequality

(3.44)

The following relation is valid for

(3.45)

Proceeding in analogous fashion with the Anti-Feynman propagator we obtain the approximation

(3.46)

4. Glaring Mistakes of Son and Starinets’ Calculation [22] Corrected

By appeal to the unproved conjecture mentioned in Subsection 1.2, Son and Starinets evaluated the retarded propagator for a scalar field in a work regarded as a standard-bear of the ADS/CFT field. They found

(4.1)

We will show below that this result is both wrong and incomplete.

The retarded propagator reads

(4.2)

For one has

(4.3)

where

(4.4)

and

(4.5)

Using [26] we have

(4.6)

This, Feynman’s propagator becomes

(4.7)

while the anti-Feynman one turns out to be

(4.8)

With the two last results OUR version of Starinets and Son retarded propagator becomes

(4.9)

and for the advanced one

(4.10)

With a little algebra the two propagators reappear as

(4.11)

(4.12)

Consider now the penultimate term of the retarded propagator. It is

(4.13)

Considering just the first term () in we can write (up to a sign)

(4.14)

that can be recast as

(4.15)

reads, using Son and Starinets’ metrics

:

(4.16)

which coincides with (4.1) after calling.

Thus, expression (4.1) is just a single term of the full expression for the retarded propagator of (4.11). This last propagator verifies while (4.1) does not. We conclude then that (4.1) CAN NOT be used as a propagator.

Starinets and Son expression (SS) (4.1) cannot be regarded as a propagator for the massless scalar field. The same happens for the Feynman propagator of Eq. (3.21) in page 9 of [22]. These erroneous results demonstrate that their conjecture is inadequate.

4.1. Son and Starinets Surprising Elimination of a Divergence

To justify the results of their paper, in page 22 of [22], Son and Starinets encounter an infinite in their equation (A.22). They eliminate it by setting, which is absurd since has a pole in, and, as a consequence, it has a divergence in this value of z. This procedure is mathematically unacceptable. However, it was applauded by many ADS/CFT practitioners. Read and learn!

5. Two Points Correlation Functions in Euclidean Space

5.1. Massless Case

To evaluate the two-point correlation function of a scalar operator, we use the result obtained in [29]. This is

(5.1)

where, , , and then

(5.2)

As, we obtain

(5.3)

Using now the expression for K given in Equation (2.20) we have

(5.4)

Accordingly, we have here arrived to the usual, well-known result.

5.2. Massive Case

For the massive case we obtain, similarly,

(5.5)

As we can write

(5.6)

Thus we arrive at

(5.7)

Now, we use the expression for given in (3.32) and write

(5.8)

or, equivalently,

(5.9)

Using now the following result, given in [26],

(5.10)

we obtain

(5.11)

Note that we have not renormalized the correlation functions. We will do that using the results of [23] in a forthcoming paper.

6. Two Points Correlation Functions in Minkowskian Space

6.1. Massless Case

Similarly to the Euclidean case we obtain for the Minkowskian one the result

(6.1)

Thus, we obtain for the Feynman’s propagator

(6.2)

For the Anti-Feynman instance one has

(6.3)

and for Wheeler’s situation,

(6.4)

6.2. Massive Case

Again, following the developments of the Euclidean case, we have, for the Minkowskian instance, the two points Feynman’s correlator:

(6.5)

Thus, we have

(6.6)

or equivalently,

(6.7)

Using again (5.10) we finally obtain

(6.8)

For the Anti-Feynman propagator we obtain in analogous fashion

(6.9)

and for Wheeler

(6.10)

Note again that we have not re-normalized the correlation functions. We will do that using the results of [23] in a forthcoming paper.

7. Conclusions

In this work we have firstly calculated, without using any conjecture, the boundary-bulk Feynman, Anti-Feynman, and Wheeler propagators (half advanced plus half retarded) for both a massless and a massive scalar field, by recourse to the theory of distributions.

We conclusively showed that a previous 2002 work by Son and Starinets [22] (discussing only the Feynman propagator) is wrong.

As further novelties, in the paper we showed that, for massive scalar fields, the expression for the boundary-bulk propagator in Euclidean momentum space does not correspond to the expression used in configuration space, but it is rather a mere approximation.

Subsequently, using the previous results, we have evaluated the correlation functions of scalar operators corresponding to massless and massive scalar fields.

Unlike the results obtained in [22], with the ones obtained here you can calculate the n-points correlation functions from gravity. This is feasible for a scalar operator when n is an arbitrary natural number. This is perhaps our main present contribution.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Maldacena, J.M. (1998) Advances in Theoretical and Mathematical Physics, 2, 231-252. https://doi.org/10.4310/ATMP.1998.v2.n2.a1
[2]	Witten, E. (1998) Advances in Theoretical and Mathematical Physics, 2, 253-291. https://doi.org/10.4310/ATMP.1998.v2.n2.a2
[3]	Gubser, S.S., Klebanov, I.R. and Polyakov, A.M. (1998) Physics Letters B, 428, 105-114. https://doi.org/10.1016/S0370-2693(98)00377-3
[4]	Danielsson, U.H., Keski-Vakkuri, E. and Kruczenski, M. (1999) Journal of High Energy Physics, 9901, 002. https://doi.org/10.1088/1126-6708/1999/01/002
[5]	Ryang, S. (1999) Physics Letters B, 469, 87-95. https://doi.org/10.1016/S0370-2693(99)01260-5
[6]	Klebanov, I.R. and Witten, E. (1999) Nuclear Physics B, 556, 89-114. https://doi.org/10.1016/S0550-3213(99)00387-9
[7]	Minces, P. and Rivelles, V.O. (2000) Nuclear Physics B, 572, 651-669. https://doi.org/10.1016/S0550-3213(99)00833-0
[8]	Mueck, W. (1999) Studies on the adS/CFT Correspondence. PhD Thesis, Simon Fraser University, Burnaby. http://www.collectionscanada.gc.ca/obj/s4/f2/dsk1/tape9/PQDD_0025/NQ51904.pdf
[9]	Mueck, W. and Viswanathan, K.S. (1998) Physical Review D, 58, 041901(R). https://doi.org/10.1103/PhysRevD.58.041901
[10]	Jepsen, C.B. and Parikh, S. (2019) Journal of High Energy Physics, 2019, 268.
[11]	Prudenziati, A. (2019) Journal of High Energy Physics, 2019, Article No. 59. https://doi.org/10.1007/JHEP06(2019)059
[12]	Parikh, M. and Samantray, P. (2018) Journal of High Energy Physics, 2018, Article No. 129. https://doi.org/10.1007/JHEP10(2018)129
[13]	Erbin, H. (2014) Scalar Propagators on adS Space. https://www.lpthe.jussieu.fr/erbin/files/ads_propagators.pdf
[14]	Balasubramanian, V., Kraus, P., Lawrence, A. and Trivedi, S.P. (1999) Physical Review D, 59, Article ID: 104021. https://doi.org/10.1103/PhysRevD.59.104021
[15]	Balasubramanian, V., Giddings, S.B. and Lawrence, A. (1999) Journal of High Energy Physics, 9903, 001. https://doi.org/10.1088/1126-6708/1999/03/001
[16]	Balasubramanian, V., Kraus, P. and Lawrence, A. (1999) Physical Review D, 59, Article ID: 046003. https://doi.org/10.1103/PhysRevD.59.046003
[17]	Wheeler, J.A. and Feynman, R.P. (1945) Reviews of Modern Physics, 17, 157-181. https://doi.org/10.1103/RevModPhys.17.157
[18]	Dirac, P.A.M. (1938) Proceedings of the Royal Society of London. Series A, 167, 148-169. https://doi.org/10.1098/rspa.1938.0124
[19]	Wheeler, J.A. and Feynman, R.P. (1949) Reviews of Modern Physics, 21, 425-433. https://doi.org/10.1103/RevModPhys.21.425
[20]	Barci, D.G., Bollini, C.G. and Rocca, M.C. (1993) Il Nuovo Cimento, 106, 603-609. https://doi.org/10.1007/BF02787229 Barci, D.G., Bollini, C.G. and Rocca, M.C. (1994) International Journal of Modern Physics A, 9, 3497-3502. https://doi.org/10.1142/S0217751X94001382
[21]	Bollini, C.G. and Oxman, L.E. (1992) International Journal of Modern Physics A, 7, 6845-6855. https://doi.org/10.1142/S0217751X92003148
[22]	Son, D.T. and Starinets, A.O. (2002) Journal of High Energy Physics, 9, 042. https://doi.org/10.1088/1126-6708/2002/09/042
[23]	Freedman, D.Z., Mathur, S.D., Matusis, A. and Rastelli, L. (1999) Nuclear Physics B, 546, 96. https://doi.org/10.1016/S0550-3213(99)00053-X
[24]	Schwartz, L. (1966) Théorie des distributions. Hermann, Paris.
[25]	Gel’fand, I.M. and Shilov, G.E. (1964) Generalized Functions. Vol. 1, Academic Press, Cambridge.
[26]	Gradshteyn, I.S. and Ryzhik, I.M. (1980) Table of Integrals, Series and Products. Academic Press, Inc., Cambridge.
[27]	Bochner, S. (1959) Lectures on Fourier Integrals. Princeton University Press, Princeton, NJ.
[28]	Jones, D.S. (1966) Generalised Functions. Cambridge University Press, Cambridge.
[29]	Nastase, H. (2015) Introduction to the AdS/CFT Correspondence. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9781316090954