1. Introduction
In various fields, there are numerous reports of varying reliability claiming to have found empirical evidence of long memory, including hydrology [1] [2] [3] [4] [5], meteorology [6] [7] [8] [9] [10], geophysics [11] [12] [13], psychology [14] [15], economics [16] [17] [18], and finance [19] - [28]. For example, Hurst [1] estimated an exponent, which measures the degree of long-range dependence, for river levels and many other geophysical time series and obtained in most cases values that are much greater than the value 0.5 characteristic for short-range dependence. Applying a new frequency-domain test, which is more robust against transitory effects than conventional tests, to an annual time series of global surface air temperature, Reschenhofer [10] found further evidence of nonstationarity (global warming). Kiss et al. [13] detected long-range correlations of extrapolar total ozone. A Fourier analysis performed by Aks, and Sprott, [14] on the time series of reversals in an psychological experiment on the human visual system showed evidence of pink noise, which is characterized by a spectral density that is inversely proportional to the frequency. Examining the persistence of various annual and quarterly measures of aggregate economic activity with fractionally integrated ARMA (ARFIMA) models, Diebold and Rudebusch [16] obtained estimates of the memory parameter d, which is related to Hurst’s exponent H by
, mostly in the range between 0.5 and 0.9, which indicates that macroeconomic shocks are persistent. Finally, Cajueiro and Tabak [21] observed decreasing estimates of H in emerging stock markets and interpreted their findings as a tendency towards market efficiency over time.
Long memory of a discrete-time stationary process can be characterized by a slowly decaying autocorrelation function satisfying
(1)
where
and
. The memory parameter d, which is also called fractional differencing parameter, measures the degree of long-range dependence. A simple example of a process, for which property (1) holds, is fractionally integrated white noise. It satisfies the difference equation
, (2)
where L is the lag operator and
is white noise with mean zero and variance
[29] and its autocorrelation function is given by
(3)
( [30], pp. 466-467), where Γ denotes the gamma function. Granger and Joyeux [31] and Hosking [32] introduced the more general class of autoregressive fractionally integrated moving average (ARFIMA) processes by extending (2) to
. (4)
Like the R package fracdiff, which will be used in our simulation study, we use the Box-Jenkins convention with reverse signs for the MA parameters. Setting d to zero, we obtain the class of ARMA processes, which have short memory because their autocorrelations decay exponentially fast.
Unfortunately, the task of distinguishing between long and short memory is far more difficult than it might appear at first glance. Pötscher [33] showed that many common estimation problems in statistics and econometrics, which include the estimation of the memory parameter d, are ill-posed in the sense that the minimax risk is bounded from below by a positive constant independent of n and does therefore not converge to zero as
. For the case when the class Y of data generating processes contains all Gaussian ARFIMA processes, he found that for any
,
, (5)
where the infimum is taken over all estimators
based on a sample of size n and the supremum is taken over all possible data generating processes. Furthermore, he showed that for every
, (5) holds also “locally”, when the supremum is taken over an arbitrarily small L1-neighborhood of
. Finally, he established that confidence intervals for d coincide with the entire parameter space for d with high probability and are therefore uninformative. Thus, drawing inferences about d appears to be a futile exercise unless restrictive assumptions on Y are imposed. Fortunately, there are applications, which do not require very rich classes of data generating processes. For example, in the case of daily return series, the class of ARFIMA processes with small p and
seems to be adequate. Fittingly, simulation studies carried out to compare different tests and estimators for d focused on ARFIMA processes with
[34] - [41].
Smith et al. [34] carried out Monte Carlo simulations, which also included the problematic case where both p and q are greater than zero, in order to compare the performance of the maximum likelihood (ML) procedure used by Dahlhaus [42] and Sowell [43], which estimates the memory parameter d simultaneously with the AR parameters
and the MA parameters
, with that of two semiparametric estimation methods, which yield only estimates of d. Both of the latter methods are frequency-domain methods. The first frequency-domain estimator is obtained from Geweke and Porter-Hudak’s [44] log periodogram regression by trimming out the contributions from the very lowest frequencies [45] and the second is a variant [46] of Robinson’s [47] average periodogram method. The results of their simulations suggest that the ML estimator is superior provided that the order (p,q) of the ARFIMA model is correctly specified. However, the ML estimator will in general be inconsistent if the model is misspecified. In contrast, consistency of the semiparametric estimators was established by Robinson [47] in case of the average periodogram method and by Hurvich et al. [48] in case of the log periodogram regression. Another advantage of the semiparametric estimators is that they are available in closed form and therefore do not require numerical methods.
In their simulation study, Reisen et al. [39] additionally investigated frequency-domain estimators that are based on the smoothed periodogram [49]. The results indicate that smoothing is indeed advantageous but trimming is not. Reschenhofer [50] explored another way to improve the performance of the log periodogram estimator. Including also log periodogram ordinates at non-Fourier frequencies, he achieved a significant decrease in the root mean square error. Again, the omission of the very lowest frequencies had a negative effect.
This paper is concerned with the estimation of the memory parameter d. A new frequency-domain estimator is proposed, which is inspired by a test for long-range dependence recently introduced by Mangat and Reschenhofer [40]. In contrast to earlier studies, which evaluated the performance of different estimators mainly in terms of the mean squared error (MSE) or the root-mean-square error (RMSE) and typically found that smoothing boosts the performance, we also stress the importance of the bias. In financial applications, estimates of d are often obtained with a rolling estimation window in order to assess the stability of the estimates over time. When the individual estimates are put together afterwards, only the variance decreases with the sample size but the bias remains fixed. Of course, a small bias is especially important for such situations. In the next sections, we will evaluate the performance of our new estimator both theoretically and empirically. First, an extensive simulation study is carried out to compare the new estimator with its competitors in terms of the bias and the RMSE. Subsequently, all estimators are applied to daily stock market indices in order to assess their practical suitability.
The paper is structured as follows. The next section reviews existing estimators and introduces the new estimator. The different estimators are compared by means of a simulation study in Section 3. Section 4 presents the results of an empirical study of both developed and developing stock markets. Section 5 concludes.
2. Frequency-Domain Estimation of the Memory Parameter
In Subsections 2.1 - 2.5, we briefly review various frequency-domain estimators for the memory parameter d, which will serve as benchmarks in the simulations presented in Section 3, before we introduce our new estimator in Subsection 2.6.
2.1. Log Periodogram Regression
The spectral density of the ARFIMA process (4) is given by
. (6)
Geweke and Porter-Hudak [44] introduced a semiparametric estimator of d that is based on a log periodogram regression. The periodogram of a sample
is defined by
. (7)
Taking logarithms and adding
to both sides of
, (8)
we obtain
. (9)
Since the ARMA component
of the spectral density
is approximately constant near frequency zero, the parameter d can be estimated by a simple linear regression with
as dependent variable and
(10)
as independent variable, where
,
, are Fourier frequencies in a small neighborhood of zero. Hurvich et al. [48] established the consistency of Geweke and Porter-Hudak’s [44] estimator
under the assumption that
and
.
2.2. Trimming
In the simple case where the observations
are i.i.d. normal with mean 0 and variance
, the normalized periodogram ordinates
are i.i.d. standard exponential and their logs are i.i.d. Gumbel with mean -γ and variance π2/6, where
is Euler’s constant. Under more general conditions, the normalized periodogram at a set of fixed frequencies still converges in distribution to a vector of i.i.d. standard exponential random variables ( [30], pp. 337-340). However, in the case of the Fourier frequencies
, only the indices are fixed whereas the frequencies move closer to frequency zero as the sample size n increases, which poses a problem particularly for ARFIMA spectral densities because they have either a zero (when d < 0) or a pole (when d > 0) at frequency zero. Indeed, Künsch [51] showed for d > 0 that the asymptotic distribution of
depends on j. Furthermore, Hurvich and Beltrao [52] and Robinson [47] showed that for both d < 0 and d > 0, the normalized periodogram ordinates
,
, are asymptotically neither independent nor identically distributed when
but the indices j stay fixed (for bounds on the asymptotic bias of the normalized periodogram and the covariance between normalized periodogram ordinates at different frequencies see [53] [54] [55]). However, Künsch [51] showed that the standard asymptotic results still hold for the Fourier frequencies
if
and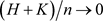 . An obvious modification of the log periodogram regression is therefore to trim the first H Fourier frequencies [45]. We denote the resulting estimator by
. An obvious modification of the log periodogram regression is therefore to trim the first H Fourier frequencies [45]. We denote the resulting estimator by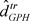 .
.
2.3. Smoothing
Hassler [56], Peiris and Court [57], and Reisen [49] proposed to replace the periodogram ordinates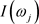 ,
, 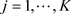 , in the log periodogram regression by the lag-window estimates
, in the log periodogram regression by the lag-window estimates
 ,
, 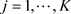 , (11)
, (11)
of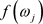 ,
, 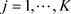 , for the spectral density f, where
, for the spectral density f, where 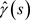 denotes the sample autocovariance at lag s and the lag window w satisfies
denotes the sample autocovariance at lag s and the lag window w satisfies ,
, 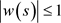 , and
, and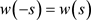 . A widely used lag window is the Parzen window
. A widely used lag window is the Parzen window
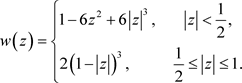 (12)
(12)
The truncation point m determines the smoothness of the estimate. For consistency it is required that  and
and 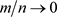 as
as . When the resulting estimator, which is based on the smoothed periodogram, is compared with the previous estimators, it is important to bear in mind that its performance depends not only on K but in addition also on m. In our simulation study, we will use the tuning parameters α, which determines the number
. When the resulting estimator, which is based on the smoothed periodogram, is compared with the previous estimators, it is important to bear in mind that its performance depends not only on K but in addition also on m. In our simulation study, we will use the tuning parameters α, which determines the number  of included periodogram ordinates, and β, which determines the truncation point
of included periodogram ordinates, and β, which determines the truncation point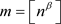 .
.
2.4. Non-Fourier Frequencies
Reschenhofer [50] modified the log periodogram regression by including non-Fourier frequencies. In this case, the amplitude R of the sinusoid
![]() (13)
(13)
can no longer be estimated by
![]() , (14)
, (14)
where ![]() and
and ![]() are the least squares (LS) estimates obtained by regressing
are the least squares (LS) estimates obtained by regressing ![]() separately on
separately on ![]() and
and![]() , because the usual orthogonality relations are only valid in case of Fourier frequencies. Instead,
, because the usual orthogonality relations are only valid in case of Fourier frequencies. Instead, ![]() and
and ![]() have to be obtained by regressing
have to be obtained by regressing ![]() simultaneously on
simultaneously on![]() ,
, ![]() , and a constant. The periodogram is then defined by
, and a constant. The periodogram is then defined by
![]() , (15)
, (15)
which is only identical to (7) in case of Fourier frequencies < π. Including the frequencies![]() ,
, ![]() in the log periodogram regression yields the estimator
in the log periodogram regression yields the estimator![]() . The frequency
. The frequency ![]() is omitted because it does not make sense to investigate cycles with periods that are twice as long as the observation period.
is omitted because it does not make sense to investigate cycles with periods that are twice as long as the observation period.
2.5. Whittle Likelihood
The task of carrying out a fair comparison between competing estimators with different numbers of tuning parameters becomes even more difficult when different types of estimators are involved, e.g., parametric, semiparametric and nonparametric estimators. Clearly, using the true dimension of the ARFIMA model, which is unknown in practice, for the calculation of the ML estimate of d would give this parametric method an unfair advantage over its competitors. Alternatively, an automatic model selection criterion could be used to choose an appropriate model. However, there are many different criteria which favor different model dimensions, hence the performance of the ML estimator will critically depend on the choice of the model selection criterion. Similarly, the performance of the nonparametric estimator obtained with Hurst’s [1] adjusted-rescaled-range approach after applying an ARMA filter to accommodate for any short-range autocorrelation also depends on the specification of the ARMA model. For example, Szilagyi and Batten [58] used an AR(1) model whereas Batten et al. [25] used different submodels of the ARMA(2,1) model.
While it is quite understandable when we do not pursue rather special approaches like nonparametric estimation based on the adjusted-rescaled-range [1] [59], which involve nonstandard asymptotics [60] [61], it is essential that we include ML estimation in one way or another. The fairest way to do so is to use the frequency-domain likelihood (Whittle likelihood) and focus on the narrow frequency band ![]() [62]. Assuming that the periodogram ordinates
[62]. Assuming that the periodogram ordinates ![]() are approximately independent exponential with means
are approximately independent exponential with means ![]() and using (8), which becomes
and using (8), which becomes
![]() (16)
(16)
in the neighborhood of frequency zero because of the constancy of ![]() and
and![]() , we obtain
, we obtain
![]() (17)
(17)
[53]. The estimator obtained by minimization of (17) over a set D of possible values of d is denoted by![]() .
.
2.6. Goodness-of-Fit Testing
Mangat and Reschenhofer [40] reduced the problem of testing hypotheses about the memory parameter d to a problem of goodness-of-fit testing. Observing that the random variables
![]() ,
, ![]() , (18)
, (18)
are under the null hypothesis ![]() approximately distributed as the order statistics of a random sample of size
approximately distributed as the order statistics of a random sample of size ![]() from a uniform distribution on [0,1], they tested the null hypothesis by applying a Kolmogorov-Smirnov goodness-of-fit test, which is based on the supremum of the differences between the hypothesized cumulative distribution function (CDF) and the empirical distribution. If
from a uniform distribution on [0,1], they tested the null hypothesis by applying a Kolmogorov-Smirnov goodness-of-fit test, which is based on the supremum of the differences between the hypothesized cumulative distribution function (CDF) and the empirical distribution. If![]() , then the CDF will be either concave or convex on (0,1), which are exactly those cases where the Kolmogrov-Smirnov is most powerful. This is crucial for the good performance of the test proposed by Mangat and Reschenhofer [40] because of the well-known inefficiency of the Kolmogorov-Smirnov test in case of more complex (e.g., multimodal) alternatives [63] [64].
, then the CDF will be either concave or convex on (0,1), which are exactly those cases where the Kolmogrov-Smirnov is most powerful. This is crucial for the good performance of the test proposed by Mangat and Reschenhofer [40] because of the well-known inefficiency of the Kolmogorov-Smirnov test in case of more complex (e.g., multimodal) alternatives [63] [64].
This approach for testing hypotheses about d can easily be adapted for the problem of estimating d. The estimation procedure proceeds as follows. First, the quantities ![]() are calculated for each element of a set D of possible values of d. In each case, a two-sided Kolmogorov-Smirnov test is applied. The p-values are ignored. Only the values of the test statistic
are calculated for each element of a set D of possible values of d. In each case, a two-sided Kolmogorov-Smirnov test is applied. The p-values are ignored. Only the values of the test statistic![]() ,
, ![]() , are of interest. The final estimate
, are of interest. The final estimate ![]() of the memory parameter is obtained by minimization of
of the memory parameter is obtained by minimization of ![]() over D.
over D.
3. Simulation Study
In this section, the performance of the different estimators for the memory parameter d is evaluated with a simulation study. The findings of this study will later be of great help for the interpretation of the empirical results obtained by applying the estimators to financial data (see Section 4). Of particular interest is the new estimator ![]() (goodness-of-fit testing), which has been introduced in Subsection 2.6. Its performance is compared with that of the competing estimators in terms of the bias and the RMSE. The other estimators included in the simulation study are
(goodness-of-fit testing), which has been introduced in Subsection 2.6. Its performance is compared with that of the competing estimators in terms of the bias and the RMSE. The other estimators included in the simulation study are ![]() (log periodogram regression),
(log periodogram regression), ![]() (trimming),
(trimming), ![]() (non-Fourier frequencies),
(non-Fourier frequencies), ![]() (simple smoothing by averaging over neighboring periodogram ordinates),
(simple smoothing by averaging over neighboring periodogram ordinates), ![]() (smoothing with Parzen window and truncation point
(smoothing with Parzen window and truncation point![]() , where
, where![]() ),
), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Bartlett window and
(smoothing with Bartlett window and![]() ) and
) and ![]() (narrow-band Whittle likelihood), where n is the length of the synthetic time series.
(narrow-band Whittle likelihood), where n is the length of the synthetic time series.
The highest frequency used for the estimation was defined by setting ![]() with
with![]() . For the calculation of
. For the calculation of ![]() and
and![]() ,
, ![]() , we used
, we used ![]() and
and
![]() , respectively. Using the R-package fracdiff, we
, respectively. Using the R-package fracdiff, we
generated 10,000 realizations of length n = 100,300,3000 of ARFIMA(1,d,0) processes with standard normal innovations, a burn-in period of 1000, and the parameter values![]() ,
,![]() . For each realization, nine different estimates were calculated. The results of this simulation study are summarized in Tables 1-6. Table 1 and Table 2 show the mean bias and the RMSE, respectively, for the case n = 100. Analogously, Table 3 & Table 4 and Table 5 & Table 6 show the results for the cases n = 300 and n = 3000, respectively.
. For each realization, nine different estimates were calculated. The results of this simulation study are summarized in Tables 1-6. Table 1 and Table 2 show the mean bias and the RMSE, respectively, for the case n = 100. Analogously, Table 3 & Table 4 and Table 5 & Table 6 show the results for the cases n = 300 and n = 3000, respectively.
The conventional log periodogram estimator serves as the main benchmark. In general, the inclusion of additional frequencies as well as simple smoothing lead to an improvement over this benchmark in terms of the RMSE whereas trimming has the opposite effect. Increasing the degree of smoothing further with the help of a lag window leads to a further improvement but the tuning parameter β, which determines the truncation point![]() , needs to be adapted. In case of larger sample sizes, larger values of β are preferable. Indeed, with a large value like
, needs to be adapted. In case of larger sample sizes, larger values of β are preferable. Indeed, with a large value like![]() , the RMSE of the lag window estimator is for
, the RMSE of the lag window estimator is for ![]() approximately of the same size as that of its main competitors
approximately of the same size as that of its main competitors ![]()
![]()
Table 1. Bias of the estimators ![]() (log periodogram regression),
(log periodogram regression), ![]() (trimming),
(trimming), ![]() (non-Fourier frequencies),
(non-Fourier frequencies), ![]() (simple smoothing),
(simple smoothing), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Bartlett window and
(smoothing with Bartlett window and![]() ),
), ![]() (narrow-band Whittle likelihood),
(narrow-band Whittle likelihood), ![]() (goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length
(goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length ![]() for
for ![]() and
and ![]() and
and![]() .
.
![]()
Table 2. RMSE of the estimators ![]() (log periodogram regression),
(log periodogram regression), ![]() (trimming),
(trimming), ![]() (non-Fourier frequencies),
(non-Fourier frequencies), ![]() (simple smoothing),
(simple smoothing), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Bartlett window and
(smoothing with Bartlett window and![]() ),
), ![]() (narrow-band Whittle likelihood),
(narrow-band Whittle likelihood), ![]() (goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length
(goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length ![]() for
for ![]() and
and ![]() and
and![]() .
.
![]()
Table 3. Bias of the estimators ![]() (log periodogram regression),
(log periodogram regression), ![]() (trimming),
(trimming), ![]() (non-Fourier frequencies),
(non-Fourier frequencies), ![]() (simple smoothing),
(simple smoothing), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Bartlett window and
(smoothing with Bartlett window and![]() ),
), ![]() (narrow-band Whittle likelihood),
(narrow-band Whittle likelihood), ![]() (goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length
(goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length ![]() for
for ![]() and
and ![]() and
and![]() .
.
![]()
Table 4. RMSE of the estimators ![]() (log periodogram regression),
(log periodogram regression), ![]() (trimming),
(trimming), ![]() (non-Fourier frequencies),
(non-Fourier frequencies), ![]() (simple smoothing),
(simple smoothing), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Bartlett window and
(smoothing with Bartlett window and![]() ),
), ![]() (narrow-band Whittle likelihood),
(narrow-band Whittle likelihood), ![]() (goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length
(goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length ![]() for
for ![]() and
and ![]() and
and![]() .
.
![]()
Table 5. Bias of the estimators ![]() (log periodogram regression),
(log periodogram regression), ![]() (trimming),
(trimming), ![]() (non-Fourier frequencies),
(non-Fourier frequencies), ![]() (simple smoothing),
(simple smoothing), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Bartlett window and
(smoothing with Bartlett window and![]() ),
), ![]() (narrow-band Whittle likelihood),
(narrow-band Whittle likelihood), ![]() (goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length
(goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length ![]() for
for ![]() and
and ![]() and
and![]() .
.
![]()
Table 6. RMSE of the estimators ![]() (log periodogram regression),
(log periodogram regression), ![]() (trimming),
(trimming), ![]() (non-Fourier frequencies),
(non-Fourier frequencies), ![]() (simple smoothing),
(simple smoothing), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Parzen window and
(smoothing with Parzen window and![]() ),
), ![]() (smoothing with Bartlett window and
(smoothing with Bartlett window and![]() ),
), ![]() (narrow-band Whittle likelihood),
(narrow-band Whittle likelihood), ![]() (goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length
(goodness-of-fit testing) obtained from 10,000 Gaussian ARFIMA(1,d,0) processes of length ![]() for
for ![]() and
and ![]() and
and![]() .
.
and![]() . When our focus is on the bias, smoothing is no longer an option because it generally increases the bias. In contrast, the inclusion of non-Fourier frequencies causes no problems in this regard. The new estimator
. When our focus is on the bias, smoothing is no longer an option because it generally increases the bias. In contrast, the inclusion of non-Fourier frequencies causes no problems in this regard. The new estimator ![]() and the narrow-band Whittle estimator
and the narrow-band Whittle estimator ![]() also perform quite well in terms of the bias.
also perform quite well in terms of the bias.
Although the mean squared error is just the sum of the squared bias and the variance and therefore strikes a fair balance between the bias and the variance, it sometimes makes sense to focus largely on only one of the two aspects. While the variance is in our simulation study typically large compared to the squared bias, the relationship is reversed in our empirical study of stock returns (see Section 4), where we perform a rolling analysis (in order to assess the stability of the estimates over time) and put the individual estimates together afterwards. In such a case, it is clearly the bias which matters more because the variance decreases steadily as the sample size increases whereas the bias remains fixed. As far as the bias is concerned, the results of our simulation study show that smoothing does not help. We may therefore expect that particularly the empirical results obtained with ![]() and
and ![]() are not reliable.
are not reliable.
4. Empirical Results
Studying emerging stock markets, Cajueiro and Tabak [21], Hull and McGroarty [65] and Auer [27] observed time-varying estimates of the Hurst exponent H. Batten et al. [25] and Auer [28] took things a step further. Assuming that fractal dynamics does in fact exist in precious metal returns, they explored possible trading strategies that are based on local estimates of H. In contrast, Reschenhofer et al. [66] found no evidence of long-range dependence, neither in stock index returns nor in gold returns. Mangat and Reschenhofer [40] and Reschenhofer and Mangat [41] developed formal statistical tests of hypotheses about d or H and applied them to stock index returns and gold returns. Again, they found no evidence of long-range dependence let alone fractal dynamics. In contrast to conventional tests, which are based on the assumption that both the length of the time series and the number of used periodogram ordinates are large and are therefore unsuitable in case of a rolling analysis, their tests require only a small number of periodogram ordinates. While we may therefore not expect to obtain estimates of the memory parameter that differ significantly from zero in the case of daily stock returns, there is a priori a much better chance of finding evidence of the presence of long memory in volatility. Accordingly, we will analyze not only the (log) returns, which are obtained as the differences of successive log prices, but also at the log absolute returns. Using log absolute returns instead of absolute returns or squared absolute returns for the investigation of volatility has the advantage that we do not have to work with extremely skewed distributions.
In our empirical study, we look for indications of long-range dependence both in developed and developing stock markets. For this purpose, six major world indices, two from America, Europe, and Asia, respectively, were downloaded from Yahoo Finance, namely S&P 500 (03.01.1950 - 26.08.2019), CCA40 (01.03.1990 - 26.08.2019), Nikkei 225 (05.01.1965 - 26.08.2019), Bovespa Index (27.04.1993 - 26.08.2019), BIST 100 (14.12.1992 - 26.08.2019), and Hang Seng Index (31.12.1986 - 26.08.2019). First we examine the return series. Applying the estimators discussed in the previous sections in a rolling analysis, we find no evidence of long-range dependence. Figure 1 shows that the estimates obtained from subseries of length 300 are consistently in a very small range around zero. The discrepancies between the estimates obtained with different estimators on the one hand or with the same estimator for different stock market indices on the other hand are therefore of no significance.
Figure 2 is analogous to Figure 1, but shows the cumulative estimates for the log absolute returns. Not surprisingly, there is strong evidence of long-range
![]()
Figure 1. Cumulative plots of the estimates obtained by applying ![]() (magenta),
(magenta), ![]() (green),
(green), ![]() (blue),
(blue), ![]() (red),
(red), ![]() (gray),
(gray), ![]() (brown),
(brown), ![]() (yellowgreen),
(yellowgreen), ![]() (gold),
(gold), ![]() (black) to the daily log returns of (a) S&P 500, (b) Ibovespa, (c) CCA 40 (d) BIST 100, (e) Nikkei 225, (f) Hang Seng Index with a rolling window of n = 300 days and K = 17.
(black) to the daily log returns of (a) S&P 500, (b) Ibovespa, (c) CCA 40 (d) BIST 100, (e) Nikkei 225, (f) Hang Seng Index with a rolling window of n = 300 days and K = 17.
![]()
Figure 2. Cumulative plots of the estimates obtained by applying ![]() (magenta),
(magenta), ![]() (green),
(green), ![]() (blue),
(blue), ![]() (red),
(red), ![]() (gray),
(gray), ![]() (brown),
(brown), ![]() (yellowgreen),
(yellowgreen), ![]() (gold),
(gold), ![]() (black) to the log absolute daily returns of (a) S&P 500, (b) Ibovespa, (c) CCA 40 (d) BIST 100, (e) Nikkei 225, (f) Hang Seng Index with a rolling window of n = 300 days and K = 17.
(black) to the log absolute daily returns of (a) S&P 500, (b) Ibovespa, (c) CCA 40 (d) BIST 100, (e) Nikkei 225, (f) Hang Seng Index with a rolling window of n = 300 days and K = 17.
dependence in the volatility. Most estimators, particularly also ![]() and
and![]() , which are approximately unbiased according to Table 3, suggest that the memory parameter d is approximately in the range between 0.2 and 0.3. Only the estimators
, which are approximately unbiased according to Table 3, suggest that the memory parameter d is approximately in the range between 0.2 and 0.3. Only the estimators ![]() and
and![]() , which are severely downward biased in case of positive d (see Table 3), favor smaller values of the memory parameter. The agreement with the results of the simulation study is remarkably good. For
, which are severely downward biased in case of positive d (see Table 3), favor smaller values of the memory parameter. The agreement with the results of the simulation study is remarkably good. For![]() ,
, ![]() ,
, ![]() , and
, and![]() , we have observed a large negative bias for
, we have observed a large negative bias for ![]() (−0.141) and
(−0.141) and ![]() (−0.115), a medium negative bias for
(−0.115), a medium negative bias for ![]() (−0.048), and a medium positive bias for
(−0.048), and a medium positive bias for ![]() (0.023). Indeed,
(0.023). Indeed, ![]() produced always (for each of the six stock market indices) the smallest estimate,
produced always (for each of the six stock market indices) the smallest estimate, ![]() the second smallest,
the second smallest, ![]() the third smallest, and
the third smallest, and ![]() the largest. The remaining estimators produced estimates that lie very close to each other, which allows to draw very accurate conclusions regarding the true value of d.
the largest. The remaining estimators produced estimates that lie very close to each other, which allows to draw very accurate conclusions regarding the true value of d.
5. Discussion
In this paper, we have converted the test of Mangat and Reschenhofer [40] into an estimator for the memory parameter which is easy to use and highly competitive. The results of our extensive simulation study show that this new estimator performs well both in terms of the RMSE and the bias. Overall, it shows the best performance together with the Whittle estimator. The estimators based on the smoothed periodogram cannot compete when the second tuning parameter β is fixed. Clearly, the possibility to fiddle about with the second tuning parameter β gives these estimators an unfair advantage over their competitors. Choosing an unsuitable value for this parameter can lead to a severe bias, which is confirmed in our empirical investigation of the long-range properties of international daily index returns. Interpreting the empirical findings properly with the help of the results of our simulation study, we conclude that the log absolute returns are long-range dependent with the memory parameter in the range between 0.2 and 0.3 in contrast to the original returns which show no indications of long-range dependence.
In conclusion, the main points of this paper are as follows. We have introduced a simple frequency-domain estimator for the memory parameter, provided evidence of its good performance relative to conventional estimators in terms of bias and RMSE, pointed out some shortcomings of the popular lag window estimators, and used the new estimator successfully to confirm the absence of long memory in stock returns and to corroborate the presence of long memory in volatility.
Acknowledgements
We thank an anonymous reviewer whose comments helped to improve our manuscript. This research was supported by grant 18051 from the Anniversary Fund of the Oesterreichische Nationalbank.