The Fekete Szegö Functional and Second Hankel Determinant for a Certain Sublass of Analytic Functions

Rasheed O. Ayinla¹, Timothy O. Opoola²

¹Department of Statistics and Mathematical Sciences, Kwara State University, Malete, Nigeria.
²Department of Mathematics, University of Ilorin, Ilorin, Nigeria.

DOI: 10.4236/am.2019.1012074                

Abstract

Let S denote the class of functions that are analytic, normalized and univalent in the open unit disk E = {z: |z| <1}. Subclasses of S are the class of starlike and convex functions denoted by S^* and C respectively. A new subclass of analytic functions that generalize some known subclasses of analytic functions was defined and investigated. We obtained coefficient bounds, upper estimates for the Fekete-Szegö functional and the Hankel determinant.

Keywords

Analytic Functions, Coefficient Bounds, Fekete-Szegö Functional, Salagean Differential Operator and Hankel Determinant

1. Introduction

Let A denote the class of functions

$f\left(z\right)=z+a_2{z}^2+a_3{z}^3+a_4{z}^4+\cdots$ (1.1)

which are analytic in the open unit disk $U=\left\{z:\left|z\right|<1\right\}$ and satisfy the condition $f\left(0\right)=0$ and $f^{\prime }\left(0\right)=1$.

Let S denote the subclass of A consisting of univalent in U. A function $f\left(z\right)\in S$ is said to be starlike in the unit disk if and only if

$Re\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}>\mathrm{0,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}z\in U$ (1.2)

Also, a function $f\left(z\right)\in S$ is said to be convex in the unit disk if and only if

$Re\left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)>\mathrm{0,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}z\in U$ (1.3)

Let $D^n\mathrm{<mo>\; :\; </mo>}A\to A$ be defined by

$D^{0}f\left(z\right)=f(z)$

$D^{1}f\left(z\right)=z{f}^{\prime }(z)$

$D^{n}f\left(z\right)=z{\left[D^{n-1}f\left(z\right)\right]}^{\prime }$

which is equivalent to

$D^{n}f\left(z\right)=z+{\displaystyle \underset{k=2}{\overset{\infty }{\sum }}}{k}^n{a}_k{z}^k,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\left(n=\left\{0,1,2,\cdots \right\}\right),\mathrm{<mi>\; </mi>\; <mi>\; </mi>}z\in U$

$D^n$ is the Salagean differential operator [1].

Fekete and Szegö [2] studied the estimate of a functional $\left|a_3-\sigma a_2^2\right|$ known as Fekete-Szegö functional, where $\sigma$ is real. Also, Noonan and Thomas [3] defined the q^th Hankel determinant of $f\left(z\right)$ for $q\ge \mathrm{1,}n\ge 0$ by

$H_q\left(n\right)=\left|\begin{array}{cccc}{a}_n& a_{n+1}& \cdots & a_{n+q-1}\\ a_{n+1}& a_{n+2}& \cdots & a_{n+q}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n+q-1}& a_{n+q}& \cdots & a_{n+2q-2}\end{array}\right|\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(a_1=1\text{for}f\left(z\right)\in S\right)$

This determinant has been considered for specific values q and n by many authors. It is well established that the Fekete-Szegö functional given by $\left|a_3-a_2^2\right|=H_2\left(1\right)$. Pommerenke [4] investigated the Hankel determinant of areally mean p-valent functions, univalent functions as well as starlike functions. Noor [5] investigated the Hankel determinant problem for the class of functions with bounded boundary rotation. Janteng et al. [6] studied the sharp upper bound for second Hankel determinant $H_2\left(2\right)=\left|a_2{a}_4-a_3^2\right|$ for univalent functions whose derivative has positive real parts. Also, Lee et al. [7] obtained bounds on second Hankel determinants belonging to the subclasses of Ma-Minda starlike and convex functions. Bansal [8] has obtained bounds on $H_2\left(2\right)$ for a new class of analytic functions.

In this paper, we obtained the coefficient bound, Fekete-Szegö functional and second Hankel determinant for the functions belonging to the subclass $C_n\left(\beta \mathrm{,}\gamma \right)$.

Definition 1.1. A function $f\left(z\right)$ of the form (1.1) analytic and univalent in U is said to be in the $C_n\left(\beta ,\gamma \right),\beta \in \left[0,1\right],\gamma \in \left(\frac{-\pi }{2}\mathrm{<mi>\; </mi>},\frac{\pi }{2}\right)$ and $n\in {\mathbb{N}}_0$ if it satisfies the inequality

$Re\left\{{\text{e}}^{i\gamma }\left(1-{\text{e}}^{-2i\gamma }{\beta }^2{z}^2\right)\frac{D^{n+1}f\left(z\right)}{z}\right\}>\mathrm{0,}z\in U\mathrm{.}$ (1.4)

Remark 1

(1) For $n=0,\beta =0$ the class $C_0\left(\mathrm{0,}\gamma \right)$ gives

$Re\left\{{\text{e}}^{i\gamma }{f}^{\prime }\left(z\right)\right\}>\mathrm{0,}z\in U$ (1.5)

studied in [9].

(2) For $n=0,\gamma =0$ gives

$Re\left\{\left(1-{\beta }^2{z}^2\right)f^{\prime }\left(z\right)\right\}>\mathrm{0,\; <mi>\; </mi>\; <mi>\; </mi>}z\in U\mathrm{.}$ (1.6)

investigated by [10].

For $n=0$, the class gives

$Re\left\{{\text{e}}^{i\gamma }\left(1-{\text{e}}^{-2i\gamma }{\beta }^2{z}^2\right)f^{\prime }\left(z\right)\right\}>\mathrm{0,\; <mi>\; </mi>\; <mi>\; </mi>}z\in U\mathrm{.}$ (1.7)

studied in [11].

2. Preliminary Lemmas

We need the following lemmas to prove our results.

Let P denote the class of Caratheodory functions.

$p\left(z\right)=1+c_{1}z+c_2{z}^2+c_3{z}^3+\cdots \mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(z\in U\right)$

which are analytic and satisfy $p\left(0\right)=1$ and $\Re p\left(z\right)>0$

Lemma 2.1. Let $p\in P$. Then

$\left|c_k\right|\le \mathrm{2\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\left(k\in \mathbb{N}\right)$ [12] (2.1)

Lemma 2.2. Let $p\in P$, then for any real $\lambda$

$\left|c_2-\lambda \frac{c_1^2}{2}\right|\le \{\begin{array}{ll}2\left(1-\lambda \right)\hfill & \text{if}\lambda \le 0\hfill \\ 2\hfill & \text{if}0\le \lambda \le 2\hfill \\ 2\left(\lambda -1\right)\hfill & \text{if}\lambda \ge 2\hfill \end{array}$ [13] (2.2)

Lemma 2.3. Let $p\in P$ then

$2c_2=c_1^2+x\left(4-c_1^2\right)$ (2.3)

$4c_3=c_1^3+2c_1\left(4-c_1^2\right)x-c_1\left(4-c_1^2\right)x^2+2\left(4-c_1^2\right)\left(1-{\left|x\right|}^2\right)z$ (2.4)

for some value of $x\mathrm{,}z$, such that $\left|x\right|\le 1$ and $\left|z\right|\le 1$ [14].

3. Main Results

Theorem 3.1. Let $f\left(z\right)\in C_n\left(\beta \mathrm{,}\gamma \right)\mathrm{,}\beta \in \left[\mathrm{0,1}\right]\mathrm{,}\gamma \in \left(\frac{-\pi }{2}\mathrm{<mi>\; </mi>,}\frac{\pi }{2}\right)$ and $n\in {\mathbb{N}}_0$.

Then

$\left|a_2\right|\le \frac{\cos \gamma }{2^n}$

$\left|a_3\right|\le \frac{2\cos \gamma +{\beta }^2}{3^{n+1}}$

Proof:

Let $f\left(z\right)\in C_n\left(\beta \mathrm{,}\gamma \right)$, then by [1.4]

$Re\mathrm{<mi>\; </mi>}{\text{e}}^{i\gamma }\left[\left(1-{\text{e}}^{-2i\gamma }{\beta }^2{z}^2\right)\frac{D^{n+1}f\left(z\right)}{z}\right]>\mathrm{0,\; <mi>\; </mi>\; <mi>\; </mi>}\gamma \in \left(\frac{-\pi }{2}\mathrm{,}\frac{\pi }{2}\right)\mathrm{,\; <mi>\; </mi>0}\le \beta \le \mathrm{1,}n\in {\mathbb{N}}_0\mathrm{,}z\in U$

Now,

$\begin{array}{l}{\text{e}}^{i\gamma }\left[\left(1-{\text{e}}^{-2i\gamma }{\beta }^2{z}^2\right)\frac{D^{n+1}f\left(z\right)}{z}\right]\\ ={\text{e}}^{i\gamma }+q_{1}z+q_2{z}^2+\cdots =\left(\cos \gamma +i\sin \gamma \right)+{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}}{q}_n{z}^n\end{array}$ (3.1)

Then

$\exists \mathrm{<mi>\; </mi>}q\left(z\right)=\cos \gamma +i\sin \gamma +{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}}{q}_n{z}^n\mathrm{,}z\in U,\mathrm{<mi>\; </mi>}n\in \mathbb{N}$

${\text{e}}^{i\gamma }\left[\left(1-{\text{e}}^{-2i\gamma }{\beta }^2{z}^2\right)\frac{D^{n+1}f\left(z\right)}{z}\right]=p\left(z\right)\cos \gamma +i\sin \gamma$ (3.2)

that is

$\cos \gamma +c_1\cos \gamma z+c_2\cos \gamma z^2+c_3\cos \gamma z^3+\cdots =\cos \gamma +q_{1}z+q_2{z}^2+q_3{z}^3+\cdots$ (3.3)

Comparing coefficients of (3.1) and (3.3) gives

$a_2=\frac{c_1{\text{e}}^{-i\gamma }\cos \gamma }{2^{n+1}}$ (3.4)

$a_3=\frac{c_2{\text{e}}^{-i\gamma }\cos \gamma +{\beta }^2{\text{e}}^{-2i\gamma }}{3^{n+1}}$ (3.5)

$a_4=\frac{c_3{\text{e}}^{-i\gamma }\cos \gamma +c_1{\beta }^2{\text{e}}^{-3i\gamma }\cos \gamma }{4^{n+1}}$ (3.6)

Solving for the bounds of (3.4), (3.5), (3.6) and using lemma 2.1 give

$\left|a_2\right|\le \frac{\cos \gamma }{2^n}$ (3.7)

$\left|a_3\right|\le \frac{2\cos \gamma +{\beta }^2}{3^{n+1}}$ (3.8)

$\left|a_4\right|\le \frac{2\cos \gamma +2{\beta }^2\cos \gamma }{4^{n+1}}$ (3.9)

Remark 2

For $n=0$

$\left|a_2\right|\le \cos \gamma$

$\left|a_3\right|\le \frac{2\cos \gamma +{\beta }^2}{3}$

Theorem 3.2. Let $f\left(z\right)\in C_n\left(\beta \mathrm{,}\gamma \right)$, then for any real number $\mu$

$\left|a_3-\mu a_2^2\right|\le \{\begin{array}{ll}\frac{{\beta }^2+2\cos \gamma }{3^{n+1}}-\frac{\mu {\text{e}}^{-i\gamma }{\cos }^2\gamma }{2^{2n}}\hfill & \text{if}\mu \mathrm{<mi>\; </mi>}\le 0\hfill \\ \frac{{\beta }^2+2\cos \gamma }{3^{n+1}}\hfill & \text{if}0\le \mu \le \frac{2^{2n+2}}{3^{n+1}{\text{e}}^{-i\gamma }\cos \gamma }\hfill \\ \frac{{\beta }^2-2\cos \gamma }{3^{n+1}}+\frac{\mu {\text{e}}^{-i\gamma }{\cos }^2\gamma }{2^{2n}}\hfill & \text{if}\mu \ge \frac{2^{2n+2}}{3^{n+1}{\text{e}}^{-i\gamma }\cos \gamma }\hfill \end{array}$

Proof:

Using (3.4) and (3.5) give

$\begin{array}{c}\left|a_3-\mu a_2^2\right|=\left|\frac{c_2{\text{e}}^{-i\gamma }\cos \gamma }{3^{n+1}}+\frac{{\beta }^2{\text{e}}^{-2i\gamma }}{3^{n+1}}-\frac{\mu c_1^2{\text{e}}^{-2i\gamma }{\cos }^2\gamma }{2^{2n+2}}\right|\\ \le \frac{{\beta }^2}{3^{n+1}}+\frac{\cos \gamma }{3^{n+1}}\left|c_2-\frac{3^{n+1}\mu {\text{e}}^{-i\gamma }\cos \gamma }{2^{2n+1}}\frac{c_1^2}{2}\right|\end{array}$ (3.10)

then using lemma (2.2) in (3.10) gives

$\left|a_3-\mu a_2^2\right|\le \frac{{\beta }^2+2\cos \gamma }{3^{n+1}}-\frac{\mu {\text{e}}^{-i\gamma }{\cos }^2\gamma }{2^{2n}}$ (3.11)

Let

$0\le \frac{3^{n+1}\mu {\text{e}}^{-i\gamma }\cos \gamma }{2^{2n+1}}\le 2$

then by lemma 2.2 we obtain

$\left|a_3-\mu a_2^2\right|\le \frac{{\beta }^2+2\cos \gamma }{3^{n+1}}$ (3.12)

suppose

$\frac{3^{n+1}\mu {\text{e}}^{-i\gamma }}{2^{2n+1}}\ge 2$

then using lemma 2.2 gives

$\left|a_3-\mu a_2^2\right|\le \frac{{\beta }^2-2\cos \gamma }{3^{n+1}}+\frac{\mu {\text{e}}^{-i\gamma }{\cos }^2\gamma }{2^{2n}}$ (3.13)

Theorem 3.3 Let $f\left(z\right)\in C_n\left(\beta \mathrm{,}\gamma \right)\mathrm{,}\beta \in \left[\mathrm{0,1}\right]\mathrm{,}\gamma \in \left(\frac{-\pi }{2}\mathrm{<mi>\; </mi>,}\frac{\pi }{2}\right)$ and $n\in {\mathbb{N}}_0$

then

$H_2\left(2\right)=\left|a_2{a}_4-a_3^2\right|\le \frac{{\beta }^4+4{\beta }^2\cos \gamma +4{\cos }^2\gamma }{3^{2n+2}}+\frac{\left({\beta }^4+6{\beta }^2+9\right)\cos \gamma }{2^{3n+4}}$

Proof:

Using (3.4), (3.5) and (3.6) give

$\begin{array}{l}\left|a_2{a}_4-a_3^2\right|\\ =\left|\frac{c_1{\text{e}}^{-i\gamma }\cos \gamma }{2^{n+1}}\left(\frac{c_3{\text{e}}^{-i\gamma }\cos \gamma +{\beta }^2{c}_1{\text{e}}^{-3i\gamma }\cos \gamma }{4^{n+1}}\right)-{\left(\frac{c_2{\text{e}}^{-i\gamma }\cos \gamma +{\beta }^2{\text{e}}^{-2i\gamma }}{3^{n+1}}\right)}^2\right|\end{array}$ (3.14)

$\begin{array}{l}\left|a_2{a}_4-a_3^2\right|\\ =|\frac{c_1^4{\text{e}}^{-2i\gamma }{\cos }^2\gamma }{2^{3n+5}}+\frac{c_1^2\left(4-c_1^2\right){\text{e}}^{-2i\gamma }x{\cos }^2\gamma }{2^{3n+4}}-\frac{c_1^2\left(4-c_1^2\right){\text{e}}^{-2i\gamma }{x}^2{\cos }^2\gamma }{2^{3n+5}}\\ +\frac{c_1\left(4-c_1^2\right)\left(1-{\left|x\right|}^2\right){\text{e}}^{-2i\gamma }{\cos }^2\gamma z}{2^{3n+4}}+\frac{c_1^2{\beta }^2{\text{e}}^{-4i\gamma }{\cos }^2\gamma }{2^{3n+3}}-\frac{c_1^4{\text{e}}^{-2i\gamma }{\cos }^2\gamma }{2^2\cdot 3^{2\left(n+1\right)}}\\ -\frac{x\left(4-c_1^2\right)c_1^2{\text{e}}^{-2i\gamma }{\cos }^2\gamma }{2\cdot 3^{2n+2}}-\frac{c_1^2{\alpha }^2{\text{e}}^{-3i\gamma }\cos \gamma }{3^{2n+2}}-\frac{x^2{\left(4-c_1^2\right)}^2{\text{e}}^{-2i\gamma }{\cos }^2\gamma }{2^2\cdot 3^{2n+2}}\\ -\frac{{\beta }^{2}x\left(4-c_1^2\right){\text{e}}^{-3i\gamma }\cos \gamma }{3^{2n+2}}-\frac{{\beta }^4{\text{e}}^{-4i\gamma }}{3^{2n+2}}|\end{array}$ (3.15)

Suppose $c_1=c$, and recall that $\left|c_1\right|\le 2$, and assuming without restriction that $c\in \left[\mathrm{0,2}\right]$. Then, using triangle inequality

(3.15) becomes

$\begin{array}{c}\left|a_2{a}_4-a_3^2\right|\le \frac{c^4{\cos }^2\gamma }{2^{3n+5}}+\frac{c^2\left(4-c^2\right)\left|x\right|{\cos }^2\gamma }{2^{3n+4}}+\frac{c^2\left(4-c^2\right){\left|x\right|}^2{\cos }^2\gamma }{2^{3n+5}}\\ +\frac{c\left(4-c^2\right)\left(1-{\left|x\right|}^2\right){\cos }^2\gamma }{2^{3n+4}}+\frac{c^2{\beta }^2{\cos }^2\gamma }{2^{3n+3}}+\frac{c^4{\cos }^2\gamma }{2^2\cdot 3^{2n+2}}\\ +\frac{\left|x\right|\left(4-c^2\right)c^2{\cos }^2\gamma }{2\cdot 3^{2n+2}}+\frac{{\left|x\right|}^2{\left(4-c^2\right)}^2{\cos }^2\gamma }{2^2\cdot 3^{2n+2}}\\ +\frac{c^2{\beta }^2\cos \gamma }{3^{2n+2}}+\frac{{\beta }^2\left|x\right|\left(4-c^2\right)\cos \gamma }{3^{2n+2}}+\frac{{\beta }^4}{3^{2n+2}}\end{array}$ (3.16)

Now, putting $\psi =\left|x\right|\le 1$ then

$\begin{array}{l}\left|a_2{a}_4-a_3^2\right|\\ \le \left\{\frac{c^4{\cos }^2\gamma }{2^{3n+5}}+\frac{c\left(4-c^2\right){\cos }^2\gamma }{2^{3n+4}}+\frac{c^2{\beta }^2{\cos }^2\gamma }{2^{3n+3}}+\frac{c^4{\cos }^2\gamma }{2^2\cdot 3^{2n+2}}+\frac{c^2{\beta }^2\cos \gamma }{3^{2n+2}}+\frac{{\beta }^4}{3^{2n+2}}\right\}\\ +\left\{\frac{c^2\left(4-c^2\right){\cos }^2\gamma }{2^{3n+4}}+\frac{\left(4-c^2\right)c^2{\cos }^2\gamma }{2\cdot 3^{2n+2}}+\frac{{\beta }^2\left(4-c^2\right)\cos \gamma }{3^{2n+2}}\right\}\psi \\ +\left\{\frac{c^2\left(4-c^2\right){\cos }^2\gamma }{2^{3n+5}}-\frac{c\left(4-c^2\right){\cos }^2\gamma }{2^{3n+4}}+\frac{{\left(4-c^2\right)}^2{\cos }^2\gamma }{2^2\cdot 3^{2n+2}}\right\}{\psi }^2=F\left(c,\psi \right)\end{array}$ (3.17)

Differentiating $F\left(c\mathrm{,}\psi \right)$ partially with respect to $\psi$ in the closed interval $0\le \psi \le 1$

$\begin{array}{c}\frac{\partial F\left(c\mathrm{,}\psi \right)}{\partial \psi }=\left\{\frac{c^2\left(4-c^2\right){\cos }^2\gamma }{2^{3n+4}}+\frac{\left(4-c^2\right)c^2{\cos }^2\gamma }{2\cdot 3^{2n+2}}+\frac{{\beta }^2\left(4-c^2\right)\cos \gamma }{3^{2n+2}}\right\}\\ +\left\{\frac{c^2\left(4-c^2\right){\cos }^2\gamma }{2^{3n+5}}-\frac{c\left(4-c^2\right){\cos }^2\gamma }{2^{3n+4}}+\frac{{\left(4-c^2\right)}^2{\cos }^2\gamma }{2^2\cdot 3^{2n+2}}\right\}\psi \\ >0\end{array}$ (3.18)

for $0\le \psi \le 1$, therefore is an increasing function. Hence, it attains maximum point at. Thus,

(3.19)

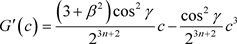
Now, the critical points occur at

but the maximum point occurring at 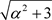[3.19] becomes

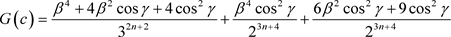(3.20)

Therefore,

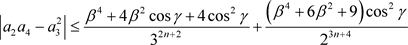(3.21)

4. Conclusion

A subclass of analytic functions which generalize some well known subclasses of analytic and univalent functions was defined. The initial coefficients upper bounds, upper estimates for the Fekete-Szegö functional and the second Hankel determinants for the class were obtained. The study unifies existing results and obtains new results in geometric function theory. Future researches can be done to obtain the geometric properties by using Chebyshev polynomials.

Acknowledgements

The authors wish to thank the referees for their valuable suggestions that lead to improvement of the quality of the work in this paper.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Salagean, S. (1983) Subclasses of Univalent Functions. In: Cazacu, C.A., Boboc, N., Jurchescu, M. and Suciu, I., Eds., Lecture Notes in Mathematics, Vol. 1013, Springer, Berlin, 362-372. https://doi.org/10.1007/BFb0066543
[2]	Fekete, M. and Szego, G. (1933) Eine Bemerkung über Ungerade Schlichte Funktionen. Journal of London Mathematical Society, 8, 85-89. https://doi.org/10.1112/jlms/s1-8.2.85
[3]	Noonan, J.W. and Thomas, D.K. (1976) On the Second Hankel Determinant of Areally Mean p-Valent Functions. Transactions of the American Mathematical Society, 223, 337-346. https://doi.org/10.2307/1997533
[4]	Pommerenke, C. (1966) On the Coefficients and Hankel Determinant of Univalent Functions. Journal of London Mathematical Society, 41, 111-112. https://doi.org/10.1112/jlms/s1-41.1.111
[5]	Noor, K.I. (1983) Hankel Determinant Problem for the Class of Functions with Bounded Boundary Rotation. Revue Roumaine de Mathématique Pures et Appliquées, 28, 731-739.
[6]	Janteng, A., Abdulhalim, S. and Darus, M. (2007) Hankel Determinant for Starlike and Convex Functions. International Journal of Mathematical Analysis, 1, 619-625.
[7]	Lee, S.K., Ravichandran, V. and Supramaniam, S. (2013) Bounds for the Second Hankel Determinant of Certain Univalent Functions. Journal of Inequalities and Applications, 2013, Article No. 281. https://doi.org/10.1186/1029-242X-2013-281
[8]	Bansal, D. (2013) Upper Bound of Second Hankel Determinant for a New Class of Analytic Functions. Application of Mathematics Letters, 26, 103-107. https://doi.org/10.1016/j.aml.2012.04.002
[9]	Noshiro, K. (1935) On the theory of schlicht functions. Journal of Faculty of Science, Hokkaido Imperial University. Series I. Mathematics, 2, 129-155. https://doi.org/10.14492/hokmj/1531209828
[10]	Lecko, A and Kanas, S. (1990) On the Fekete-Szego Problem and the Domain of Convexity for a Certain Class of Univalent Functions. Folia Scientiarum Universitatis Technical Resolviensis, 73, 49-56.
[11]	Lecko, A. (1993) Some Generalizations of Analytic Condition for Class of Convex in a Given Direction. Folia Scientiarum Universitatis Technical Resolviensis, 121, 23-24.
[12]	Duren, P.L. (1983) Univalent Functions. Graduate Texts in Mathematics. Springer-Verlag. New York Inc., New York.
[13]	Babalola, K.O. and Opoola, T.O. (2006) On the Coefficients of Certain Analytic and Univalent Functions. Advances in Inequalities for Series. Nova Science Publishers, 5-17.
[14]	Libera, R.J. and Zlotkiewicz, E.J. (1983) Coefficient Bounds for the Inverse of a Function with Derivative. Proceedings of American Mathematical Society, 87, 251-257. https://doi.org/10.2307/2043698