The Impacts of Population Aging on Saving, Capital Formation, and Economic Growth

Yuan-Ho Hsu^1*, Huei-Chun Lo²

¹Department of Economics, National Cheng Kung University, Taiwan, China.
²National Open College of Continuing Education, Taichung University of Science and Technology, Taiwan, China.

DOI: 10.4236/ajibm.2019.912148                

Abstract

The evolving population aging scenarios of the industrialized countries can be attributed to two major demographic dynamics: the declining fertility and fast aging population. The increasing old age dependency ratio, decreasing young dependency ratio, and shrinking share of working-age population in the aging economies generate substantial impacts on individual as well as aggregate consumption, saving and employment. Because retired people save less, an aging society with increasing proportion of retirees would experience a decline in aggregate savings, which in turn leads to lower capital formation and reduces economic growth. This paper focuses on the effect of population aging on aggregate saving, physical capital formation, and economic growth in Japan. The current study theorizes the effect of aging demographic dynamics on savings and capital formation. Taking into account the effects of population dynamics, saving, and capital formation together, this paper steps further in examining the implications of population aging for economic growth and discusses policy implications for the aging economy.

Keywords

Population Aging, Saving, Capital Formation, Economic Growth

1. Introduction

The evolving population aging scenarios of the industrialized countries can be attributed to two major demographic dynamics: the declining fertility and fast aging population. The increasing old age dependency ratio, decreasing young dependency ratio, and shrinking share of working-age population in the aging economies generate substantial impacts on individual as well as aggregate consumption, saving and employment. Since retired people save less, an aging society with increasing proportion of retirees would experience a decline in aggregate savings, which in turn leads to lower capital formation and reduced economic growth. This paper focuses on the effect of population aging on aggregate saving, physical capital formation, and economic growth in Japan.

The newborn population in Japan peaked at 2,091,983 in 1973 and then steadily declined to 1,071,304 in 2010. In 2017, the number of newborn population further declined to 946,065. On the other hand, the proportion of people aged 65 and over has reached 23% in 2010 and is expected to reach 32% by 2030. In order to analyze the effect of this demographic development on aggregate economic performance, this paper adopts Japanese population statistics published by the Statistics Bureau, Ministry of Internal Affairs and Communications, together with the latest population projection made by National Institute of Population and Social Security Research (IPSS), Japan. Figure 1 illustrates the age compositions of historical and forecasted Japanese population from 1946 to 2065. A vertical line drawn on year 2016 in Figure 1 divides the Japanese population scenarios into historical and forecasted parts; to the left of this vertical line is the historical data adopted from Statistical Bureau of Japan and to its right is the forecasted series taken from National Institute of Population and Social Security Research, Japan. In this graph, a data labeled with suffix “H” signifies historical data (e.g., POPH) and data labeled with suffix “F” represents forecasted series.

The left panel of Figure 1 indicates that Japanese aggregate population had reached its climax around 2010. However, the working age population, people with age 16 to age 64, had already reached its peak circa 1995 (see AGE1564H in the right panel). The right panel of Figure 1 also shows that the number of young-age population (AGE0014) has been shrinking rapidly while the old-age people (AGE65up) has increased rapidly between 1950 and 2010. The size of old-age population will continue to increase up to the time circa 2050 and decline

Figure 1. Total population and the size of three age-groups. Data Source: Population Estimates of Japan, 1920-2015, Statistics Bureau Japan; Population Projections for Japan (2016-2065), National Institute of Population and Social Security Research, Japan.

slowly thereafter. The forecasted size of young generation, people aged 0 - 14 (AGE0014F), shows a continuous declining trend in the future. Comparing the forecasted age compositions of Japanese population, it is noticeable that the continuing decline in the proportion of the working-age population (i.e., people aged 15 - 64) is an alarming signal for future economic development and social welfare expenditures in Japan.

Various studies have examined the implications of these evolving demographic dynamics in Japan. Some addressed aging effect on saving behavior (Horioka [1] ; Iwaisako and Okada [2] ); others focused on its labor market effects (Ito [3] ; Ogawa et al. [4] ), and some others investigated overall macroeconomic effects of population aging in Japan (e.g. Muto et al. [5] ). Razin et al. [6] and Bloom et al. [7] investigated the implications of population aging on social welfare and old-age health care. Of all these published works, one issue that has not been fully investigated is the effect of demographic transition on capital accumulation and its consequence on labor productivity and economic growth. Therefore, the current paper wishes to bridge the gap and focuses on the macroeconomic effect of population aging on capital formation and economic growth in the aged economy.

It is recognized that capital accumulation enhances overall quality of the nation’s workforce and thus contributes to economic growth and national competitiveness. The effect of aging population on capital formation is an issue worth exploring. In order to have a better understanding of the dynamic interactions among various macroeconomic variables, this paper use Japan as an example to explore the effects of population aging on national saving, and thus national saving on capital formation and economic growth.

This research adopts data from National Tax Agency of Japan, Penn World Table(PWT) version 9.1, and the 2019 Revision of the World Population Prospects,¹ ranged 1968-2100. The study first builds a theoretical growth model which takes into account of life-cycle saving behavior, life-cycle income capability, and age-composition dynamics to investigate the effect of population aging on aggregate savings. Then, it goes further to elaborate the effect of age structure change on savings, physical capital formation, and economic growth, respectively, under alternative hypothetical scenarios.

The remainder of this paper is organized as follows. Section 2 reviews previous literatures of population aging, saving and economic growth. Section 3 illustrates the specification of theoretical model and methodology employed in this study. Section 4 presents the major findings of this work and discusses policy implications drawn from this study. Section 5 draws conclusions from this study and presents extension to discuss policy implications from this research.

2. Literature Reviews

The research interest of this study focuses on the effects of demographic structure change on national saving and economic growth in Japan. The existing knowledge doesn’t have consensus on the effects of population change on economic performances; some argue that population has positive effect on economic growth whereas others maintain opposite argument. Furthermore, most existing literatures in economic development studies relate population growth to economic growth, not on the correlation between population aging and economic growth. This section first reviews existing literatures on the relationship between aging and saving, and then on the relationship between saving and economic growth.

The canonical work of Modigliani and Brumberg [8] developed a theory of consumer expenditure based on life-cycle income and consumption of households, which is known as the life-cycle hypothesis (LCH). Based on the well-known life-cycle consumption and savings, households accumulate their wealth in the middle-age when they are at the peak of earnings capability and make precautionary saving for the needs after retirement. On the retirement ages they de-cumulate their asset holdings for consumption. According to the LCH, the age-saving profile is hump-shaped which represents worker’s saving capability across life span. That is, people save less at young and old age, comparing to their savings in the working ages. Population aging signifies a relative increase in the size of low saving old-age group, which naturally leads to a downward pressure on aggregate saving.

Ando and Modigliani [9] examined the Modigliani & Brumberg [8] life-cycle hypothesis in the United States for the period of 1929-1959 and found evidences to support that hypothesis. Higgins [10] found that youth dependency ratio and old dependency ratio are significant determinants of saving rate in a sample of 100 countries. Higgins’ investigation coincided with much of the prior literatures surveyed in Ando and Modigliani [9] and Horioka [1] in which demographic transition has substantial effects on national savings rates in Japan and United States, so that it predicted that Japan’s saving rate would decline sharply in the coming decades due to rapid population aging. However, Iwaisako and Okada [2] argued the monotonic trend of population aging alone can’t explain the nonlinear movement in Japanese household saving rate, though household saving rate showed accelerated decline after the economic crisis in 1997-1998 as predicted yet the same rate decelerated around 2004-2005 and thereafter. They maintained that the scenario of sharp saving rate decline are due to decline in household income growth, not population aging. Li et al. [11] investigated the effects of China’s demographic changes on labor supply and the effects of human capital improvement on savings and investment. They found that the increasing savings and investment rates of Chinese aging population fostered economic growth in China. Wong and Tang [12] examined the effect of population aging on private saving in a panel data of 22 OECD countries from 1961 to 2010 and concluded that longevity has a significant positive impact on savings, while the effect of old-aged dependency rate is not obvious.

We have reviewed the literature on the effects of population aging on national saving; we proceed to review literatures exploring the correlation between saving and economic growth. The acknowledged theoretical investigation of the effect of saving on economic growth dated back to Harrod [13], Domar [14] [15], and Solow [16]. Given that aggregate output is the function of physical capital and labor inputs, these models proposed that economic growth depends on saving rate and that higher saving rate contributes to higher economic growth. In the exploration of source of economic growth, the extended model incorporated one demographic variable, population growth rate, and investigated the effect of population growth on economic growth. However, in these growth models population growth rate is assumed to be positive and constant. Neither a negative growth rate of the population, nor a shift in the age structure is considered in these models. Over the later decades, studies of economic growth model have extended previous works by taking into account additional factors, such as technology, human capital, urbanization, institutions, openness to international trade, and geographic factors, in the determination of economic growth.²

Most recent development in growth theory, the endogenous growth theory whose pioneer studies are Romer [24], Lucas [25], and Rebelo [26], considers saving rate as one of the key determinants of economic growth. It predicts that an increase in the saving rate will lead to a permanently higher growth rate. However, these empirical studies on the relationship between economic growth and savings have not reached unanimous conclusion, due to their difference in the methods, periods of study, and countries being selected for studied. Miller [27] found the cointegrated relation between national saving and domestic investment rate in the US only existed prior to 1971. Kim and Lee [28] used panel Vector-Auto Regressive (VAR) model and found negative effects of population aging on national saving and current account balances in East Asia. Kumar Narayan [29] used the bound testing approach of cointegration analysis to investigate the correlation between saving and investment for Japan over the period 1960-1999; the empirical results indicated that saving and investment are cointegrated with bidirectional causality. Andrei and Huidumac-Petrescu [30] examined the long-run relationship between saving and the real economic growth for Euro area countries. Their empirical results showed the existence of a unidirectional causality from real GDP growth rate to gross national saving rate. Bayar [31] used panel cointegration tests and vector error correction model in the study and found that domestic savings, domestic investment and foreign direct investment had positive effect on economic growth in emerging Asian economies for the period 1982-2012.

Many empirical studies address the effect of demographic transition on household savings behavior and economic growth. Most findings support the predictions of the LCH and OLG models, particularly with respect to the positive influence of the proportion of working-age population on national saving rates, while the effect of old-age population on saving is less conclusive. For example, Braun et al. [32] found the Japanese demographic factors account for the decline in Japan’s national saving rate in the 1990s. Bloom et al. [33] demonstrated the demographic dividends of the working-age population for economic growth. Li et al. [11] examined the effects of demographic structure on economic growth by using 29 provincial panel dataset in China and found that the old age dependency ratio has a positive effect on savings, investment, and economic growth rate. Bloom et al. [7] argued population aging will lower labor force participation and savings rates, which leads to decline in economic growth.

3. Model Specification and Methodology

According to Harrod [13], Domar [14] and Solow [16], saving is a key driver to economic growth. The current study investigates the effects of population aging on economic growth based on the idea of the life-cycle hypothesis of Modigliani and Brumberg [8] and the saving-growth connection of Harrod-Domar-Solow schema. Since saving varies with individual’s age-specific position in his/her life span and working-age population are the major savers of the economy, it is foreseeable that population aging alters relative share of working-age cohort and hence the economy’s aggregate savings. As a result, the current study assumes that changes in demographic structure exert potentially effects on national saving.

The current study theorizes the effect of demographic dynamics on savings and capital formation in an aging economy. Taking into account the effects of population dynamics, saving, and capital formation together, this effort allows us to go one step further in examining the implications of population aging for economic growth. With this endeavor, the current study modifies Solow’s growth model and allows saving rate to vary with change in age structure of population, which is in accordance to the life-cycle hypothesis of saving. This revision of age-related saving behavior would allow us to analyze the effect of population aging on aggregate savings and per capita income.

Consider a simple closed economy with no government that all output (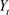) is either used for consumption (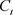) or investment (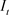). The national income identity is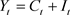. Investment (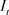) is used to create new units of physical capital (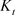) or to replace old, worn-out capital (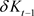). Subtracting 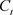from both sides of the national income identity, one obtains national saving: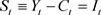. In equilibrium, the amount saved equals to the amount invested. Investment makes new injection to existing capital stock whereas depreciation wipes out a certain portion of existing capital. Assume that the capital stock wears out at a constant depreciation rate δ. Savings finance investment projects so that the amount of capital accumulation is determined by proportion of income saved; that is, the saving rate s. At any given level of income, higher saving rate implies higher saving and investment.

Assume that aggregate output is a function of technology, physical capital, and labor with a standard Cobb-Douglas aggregate production function of constant returns to scale:

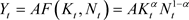(1)

where 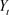is aggregate output or gross domestic product (GDP); A denotes a “Hicks-neutral” technological progress. The input factors, and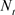, represent physical capital and labor, respectively. 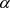and are the partial production elasticities of physical capital and labor and they are also the shares of physical capital and labor in income. Economic growth is determined by the growth of three elements: technological progress (A), physical capital (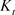) and labor input ().

Assume population grows at a constant rate of n and labor grows at the same rate as aggregate population. Technological advancement as well as increase in physical capital and labor inputs raises production productivity. Define k as the stock of physical capital per unit of labor () and as the level of output per unit of labor (). One can re-write (1) in terms of output per capita and yields³

(2)

Taking natural logarithms of (2) and calculating the first difference, one obtains growth rate of output per capita:

(3)

Equation (3) shows that the growth rate of GDP per capita is determined by the growth rate of technological progress () and the product of output elasticity of capital and the growth rate of physical capital per labor ().

In Solow’s model, saving contributes to the accumulation of the physical capital stock which increases the labor efficiency of production. However, the saving rate in Solow’s model is assumed to be constant over time. According to life-cycle hypothesis (LCH) individual saving varies with age; the empirical data from “Family Income and Expenditure Survey” of Japan also shows that saving and consumption is age-dependent. As a result, it would be confidently to take household head as a representative individual in the economy and relate his/her age to income and expenditure at different ages. Figure 2 illustrates the profile of income and expenditure of the average household at different ages in 2018. The figures shown in Figure 2 are yearly average of monthly income and disbursements per household of various age groups in 2018, which is adopted from Japanese Family Income and Expenditure Survey of Two-or-more-person Households.⁴ Although income and expenditure may differ across years due to economic fluctuations, both series reveal a common pattern across age groups. That is, both income and expenditure are hump-shaped which increase with ages up to age 55 and decline thereafter. A young representative household

Figure 2. Monthly income and expenditure per household head by age groups in 2018. Source: Yearly Average of Monthly Receipts and Disbursements per Household in Family Income and Expenditure Survey by Statistical Survey Department, Statistics Bureau, Ministry of Internal Affairs and Communications.

earns monthly income of ¥479,323 and spends ¥328,837 monthly in 2018. As age increases earning capability increases and expenditure increases as well. Both income and expenditure series show an increasing trend up to age 55 and drop after age 55 - 59. For people with old age, though both income and expenditure decreased, expenditure shows a smoother scenario than scenario of income. This scenarios difference is due to the Japanese job market convention and public pension provision. In the post-WWII era, the conventional retirement age in Japan is 55 and the government pension provision starts at age 60. As a result, many retirees are forced to search for various kinds of works to earn provisional income to cover the income shortage in this 5-year gap. Re-entrée of the old age workers is difficulty in Japanese economy because most jobs are for young or middle age workers. Due to this institutional factor, income drops sharply for Japanese people aged 60 - 64.

Figure 3 illustrates the life-cycle scenario of average propensity to save (APS, the ratio of surplus to income) per Japanese household head from 2015-2018. Comparing with other years, 2018 is the year that people save more out of their income. However, the saving behavior of a typical household head at different ages shows similar saving pattern across years. Moreover, young people tends to have a higher APS than the middle-aged and the elders. In 2018, the young cohort (age 34 and less), though has the lowest income comparing to the other middle-age cohorts, has the highest saving rate which is 34.2%. When people approaches retirement age of 55, APS increases slightly and then drops sharply around age 60. In 2018, the APS for the retiree cohort (age 60 - 64) is only 9.1%, whereas the APS of this age cohort is less than 3% in the previous three years.

From the Japanese household survey data one observes that both household’s income and expenditure reveal an inverted U-shape. One also notices that the Japanese household saving rates decrease with age, up to the middle-age around age 50 - 54, and then increase while approaching to the brink of retirement age

Figure 3. Average propensity to save (%) per household head by age groups, 2015-2018. Source: Ratio of surplus to disposable income (%) in Family Income and Expenditure Survey by Statistical Survey Department, Statistics Bureau, Ministry of Internal Affairs and Communications, Japan.

of 55 - 59. In the first instance of retirement, the saving rate of the elderly drops noticeably, comparing to that of the other working ages. Moreover, saving rate of the elderly does not drop to zero or negative as predicted by the life-cycle hypothesis.

Although the validity of the life-cycle hypothesis is still subject to debate, the Japanese household survey data shows that both consumption and savings of a typical household vary across individual’s life span. Therefore, one would expect that changes in the age structure of population would alter the time path of aggregate saving and saving rate per capita. To illustrate this argument, let’s define the aggregate saving at time t () to be the sum of individual saving at every age i at time t () multiplied by the number of population at that age (). That is,

(4)

where is the aggregate saving at time t, is the saving rate of individual aged i at time t, is the average income of people aged i at time t, and is the number of population of age i at time t. The life expectancy is 80 in this computation.

Rewrite Equation (4), one obtains saving per capita () which is a function of relative share of each age group to total population (). That is,

(5)

Furthermore, saving rate per capita can also be expressed as a function of relative age composition of each age group to total population:

(6)

In order to capture the impact of demographic structure change on saving rate, one can express aggregate saving rate, , alternatively as:

(7)

Equation (7) states that aggregate saving rate is the sum of two products: age-specific saving rate () and share of age $i$ ’s income to aggregate income ();

(8)

where and.

Income per capita can also be written as a function of the population’s age structure:

(9)

where is GDP (total income), is total population, is total income by age $i$, is the average income of age $i$ cohort, and is the number of wage earners at age $i$.

This paper assumes savings are used to finance the accumulation of physical capital only. The dynamic of the capital stock over time in Solow’s growth model is determined by the increment of capital stock () which is shown in (10):⁵

(10)

In Equation (10) the increment of capital is the residual of new injection of capital, gross investment (), minus the amount new capital that is required to replace worn-out capital and to equip the needs of new capital resulting from the increased new workers (). The current study modifies Solow’s growth model by considering the impact of demographic change on saving, capital formation, and economic growth. There are two changes in this model, with respect to that of Solow growth model: the first modification is the exogenously population growth rate (n) and the second is the saving rate (s). In Solow’s model both rates are assumed to be constant and exogenously given. In this paper both rates are assumed to be determined by demographic transition and vary over time as population structure changed. The behavior of saving rate in this model has been illustrated in (7), here we introduce the determination of population growth rate at time t:

(11)

where b_t is the crude birth rate and d_t is the crude death rate; both b_t and d_t are determined independently from contemporaneous economic factors. As a consequence, n_t is the net rate of increase in total population at time t. There is no immigration in this specification.

The model system used in this study consists of four equations which are summarized as followings:

(2')

(6')

(10')

(11')

4. Empirical Estimation and Simulations

It has been shown that population aging alters age composition of the population which in turn affects labor supply and physical capital formation. This section investigates the dynamic correlation among population age structure, saving, capital accumulation, and GDP growth. In the demographic aging process, the size of labor force in the economy shrinks as the age structure of total population changed. Moreover, according to the life cycle hypothesis, people at old age save less than the middle ages. Therefore, the empirical model includes demographic factor in the context of saving, capital accumulation and economic growth estimation.

The simulation exercise uses the medium variant population projections, 2016-2065, made by National Institute of Population and Social Security Research in Japan as baseline population input for calibration.⁶ Model calibration and validation has been conducted for years 2016 to 2065.

Based on the LCH, old-age people save less than that of the prime-age working population. As a result, one would expect that increasing share of old age population in the economy would lead to a decline in average saving per head. Figure 4 illustrates the time path of the simulated scenarios of GDP, capital stock, aggregate saving (), saving per capita () and the corresponding growth of

Figure 4. Growth rate of key variables in the model, baseline scenarios. Sources: Authors’ simulation.

these four variables. The simulation results indicate that both aggregate saving and saving per capita reveal upward trend (left panel, 3rd and 4th rows of Figure 4), which do not conform to the prediction based on the LCH proposition. However, as population aging evolves both the rate of change in aggregate saving and per capita saving decrease remarkably. One notices that both rates of change in aggregate and per capita saving decrease drastically, drop from roughly 28% to 5% in 10 years. After 10 years, both rates keep decreasing, though only decrease mildly, and then stagnate around 1% in the long-run. The simulated results also indicate that saving rate () also decreases with population aging (Figure 5). The simulated saving ratio declines from 0.205 in 2018 to 0.18 in 2065, and stagnates around that rate in the long-run. Therefore, on significant finding of this paper is that the simulated results from this paper confirm that population aging will lead to a decline in the saving rate and saving out of current income, not the aggregate level of saving predicted by LCH.

The baseline model indicates that, absent from any counteracting force to deter the effects arising from population aging, per capita output growth and hence the living standard per capita (1st row in Figure 4) in Japan will experience modest decline in the decades to come. Given these alarming scenarios, we are interested in exploring possible policy measures that can be used to mitigate this alarming development.

This paper considers two different saving behaviors of the aging economy and their effects on GDP growth: 1) Being concerned about the reduction in future income, people may save more while they are still working. Therefore, the first experiment considers an increase in saving rate of all age groups. 2) While all age groups may increase their savings, which age group’s saving has the most prominent effect on GDP growth?

The effects of increasing saving rates of all age groups have positive effect in promoting output growth (Figure 6). However, the effect of continuous increases

Figure 5. Simulated scenarios of saving rate (S/Y) in the aged economy of Japan. Sources: Authors’ simulation.

Figure 6. Increase saving rate of all age groups. Sources: Authors’ simulation.

per annum by 1% yields more prominent effect than a one-time increase of 3%. However, in order to enjoy the long-run fruit of improved GDP growth, resulting from saving increase, people has to endure a short-run suffering of declined economic growth. The simulated scenarios in Figure 6 show that there is approximately a five-year period of downfall in growth rate due to increased savings before people can enjoy higher economic growth.

Current savings inject to future capital stock and hence increase future economic growth. However, which age group’s saving has contribution that is more noticeable than the other age groups? The young workers? The middle-age working group? Or the late middle-age working group? This paper conducts a simulation on the effects of increasing savings in four age groups: the young workers aged 20 - 24; the prime age cohort of the labor force aged 35 - 39 and 45 - 49, and the group who is nearing retirement, namely, workers aged 60 - 64. The simulated results in Figure 7 indicate that a same percentage increase in the saving ratio of the prime working-age population generates most impressive effects on GDP growth than that of the other age groups. This result may not be surprisingly because income of this cohort is higher than that of the other age cohorts, so that the volume of income saved injects more to capital stock and yields more output in the future. Therefore, our model shows that a continuous increase in saving rates generates obvious effects on capital formation and output growth, especially for the prime saving age cohorts (Figure 7).

Population aging leads to a reduction in the working age population and a increase in the dependent elder population. Although the demographic development of population aging inevitably leads to a reduction in future economic growth, the shrinking volume in labor force may countered by improvement in productivity. A final experiment of this paper considers the effects of technological

Figure 7. Increase saving rate of the young working-age group. Sources: Authors’ simulation.

advancement or productivity growth on economic growth in the aging economy. The simulation experiments consider a one-time jump of technology and continuous improvement of production technology. Comparing the scenarios of baseline and alternative productivity advancement hypothesis, it is noticeable that a steady continuous technological advancement can produce prominent improvement on GDP growth than that of either one-time technological jump or no productivity progress cases (Figure 8).

5. Discussions and Policy Implications

This study explores the impact of population aging on saving and physical capital accumulation in Japan. The effect of population aging on economic growth has been investigated via two channels, the labor productivity channel and labor supply channel. The current study concentrates on the first channel that illustrates how population aging affects the capital accumulation, capital intensity and multi-factor productivity. This study also performs various hypothetical experiments trying to identify factors that can be used to compensate for the negative effect of declining labor supply resulting from population aging.

The life-cycle hypothesis maintains that an individual’s life time income and

Figure 8. The effects of productivity growth in the aged economy of Japan. Sources: Authors’ simulation.

saving are related to his/her age at life span. The profiles of life-time income and saving of a representative individual are inverted U-shaped. Given the life-time saving profile, an elderly person would have less income and save less than a middle-age worker does. As a result, in an aging economy where there is an enlarging proportion of elders and relatively small and shrinking working-age population, one would expect that population aging would affect aggregate savings and capital formation. The baseline simulation indicates a decaying trend of economic growth rate. The experiments show that a continuous increase of the saving rate produces favorable effects relative to one-time increase of saving rate. Moreover, the growth effects of total factor productivity are larger than the effects of saving rate in the future.⁷ In view of the LCH, it comes as no surprise that the impacts of saving rate of young age and old age population are small.

In the current study, we distinguish between the young, prime and old age populations according to LCH. The results imply that the ongoing aging process is expected to adversely affect the economy. Though the growth effects of separate saving rates are small, the overall higher saving rates of all age groups have the potential to give rise to economic growth. Measures to encourage continuous increase in saving rate of the prime age population or whole economy can mitigate the adverse effects of population aging on GDP growth.

Labor shortage due to population aging is a challenge to economic growth in the aging economy. From the demographic prospective, this challenge is the result of falling fertility and lengthening of longevity. To mitigate the adverse impacts of population aging on the volume of labor force and economic growth, some people propose policy measures that encourage fertility and promote child welfare, such as increases in child care facilities and make direct subsidies or tax rebates to child bearing, and wish these measures may work to increase fertility. However, parenting involves many unforeseeable opportunity costs and requires both mental and physical perseverance to raise the young siblings; government policy encouragement may not produce enough incentive to increase fertility. Even if the government could effectively promote the fertility rate, its effect to economic growth can only be effective sixteen years later when the newborn siblings grow up and are suitable to undertake physical works. Therefore, a more reasonable measure to mitigate the challenge is to improve the labor market efficiency to increase labor force participation rate and to create old-age friendly employment environment so that encouraging re-entry of the healthy retirees to the labor market. Additional policy measures to postpone the mandatory retirement age can also be used, so that the healthy elders can stay longer in the labor market.

Another important policy measures in the aging economy is to improve total factor productivity to counter the adverse effect on economic growth arising from shrinking labor input. The simulation experiments in this study have shown that increase in total factor productivity has more prominent effect on economic growth than encouraging saving and capital formation. Policy measures that encourage research and development (R&D) to promote innovation and technological progress may be the most useful and viable measures to mitigate the adverse effect of population aging on economic growth. Moreover, increasing human capital formation is also an important policy measure because it improves labor quality and productivity, so that the adverse “volume” effect of population aging on labor force can be partially offset by the improvement in the labor productivity.

NOTES

¹Population Division, Department of Economics and Social Welfare, United Nations. Available at: http://esa.un.org/wpp/.

²For example, see Becker et al. [17], Romer [18], Barro [19], Barro and Lee [20] ; Mankiw et al. [21], Jones [22], and Bloom et al. [23].

³ $y_t=\frac{Y_t}{N_t}=\frac{A{K}_t^{\alpha }{N}_t^{1-\alpha }}{N_t}=A{\left(\frac{K_t}{N_t}\right)}^{\alpha }\cdot N_t^{1-\alpha -1+\alpha }=A{k}_t^{\alpha }$

⁴The data series is available at: https://www.e-stat.go.jp/dbview?sid=0002070011.

⁵Assume in a closed economy, $Y=C+I=C+S$ and $y=c+i=c+s$. $\begin{array}{c}\Delta k=\frac{\text{d}k}{\text{d}t}=\frac{\text{d}\left(\frac{K}{L}\right)}{\text{d}t}=\frac{L\cdot \left(\frac{\text{d}K}{\text{d}t}\right)-K\cdot \left(\frac{\text{d}L}{\text{d}t}\right)}{L^2}=\frac{\frac{\text{d}K}{\text{d}t}}{L}-K\cdot \frac{nL}{L^2}=\frac{I_k-\delta K}{L}-\frac{Kn}{L}\\ =i_k-\delta k-nk=sr\cdot y-\left(\delta +n\right)k\end{array}$

⁶Population Projections for Japan: 2011-2060 by National Institute of Population and Social Security Research in Japan. Available at: http://www.ipss.go.jp/index-e.asp.

⁷Solow [16] treats total factor productivity as a residual in his growth accounting; that is, the part of output growth that cannot be explained by changes in inputs of capital and labors. In other words, total factor productivity is attributable to the efforts of R&D that leads to innovation and technological and organizational improvement.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Horioka, C.Y. (1990) Why Is Japan’s Household Saving Rate So High? A Literature Survey. Journal of the Japanese and International Economies, 4, 49-92. https://doi.org/10.1016/0889-1583(90)90012-U
[2]	Iwaisako, T. and Okada, K. (2012) Understanding the Decline in Japan’s Saving Rate in the New Millennium. Japan and the World Economy, 24, 163-173. https://doi.org/10.1016/j.japwor.2012.04.003
[3]	Ito, T. (1996) Japan and the Asian Economies: A “Miracle” in Transition. Brookings Papers on Economic Activity, 1996, 205-272. https://doi.org/10.2307/2534622
[4]	Ogawa, N., Kondo, M. and Matsukura, R. (2005) Japan’s Transition from the Demographic Bonus to the Demographic Onus. Asian Population Studies, 1, 207-226. https://doi.org/10.1080/17441730500317451
[5]	Muto, I., Oda, T. and Sudo, N. (2016) Macroeconomic Impact of Population Aging in Japan: A Perspective from an Overlapping Generations Model. IMF Economic Review, 64, 408-442. https://doi.org/10.1057/imfer.2016.6
[6]	Razin, A., Sadka, E. and Swagel, P. (2002) The Aging Population and the Size of the Welfare State. Journal of Political Economy, 110, 900-918. https://doi.org/10.1086/340780
[7]	Bloom, E.D., Boersch-Supan, A., McGee, P. and Seike, A. (2011) Population Aging: Facts, Challenges, and Responses. PGDA Working Paper No. 71. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.697.7186&rep=rep1&type=pdf
[8]	Modigliani, F. and Brumberg, R.H. (1954) Utility Analysis and the Consumption Function: An Interpretation of Cross-Section Data. In: Kurihara, K.K., Ed., Post-Keynesian Economics, Rutgers University Press, New Brunswick, 388-436.
[9]	Ando, A. and Modigliani, F. (1963) The “Life-Cycle” Hypothesis of Saving: Aggregate Implications and Tests. American Economic Review, 53, 55-84.
[10]	Higgins, M. (1998) Demography, National Savings, and International Capital Flows. International Economic Review, 39, 343-369. https://doi.org/10.2307/2527297
[11]	Li, X., Li, Z.G. and Chan, M.L. (2012) Demographic Change, Savings, Investment, and Economic Growth. Chinese Economy, 45, 5-20. https://doi.org/10.2753/CES1097-1475450201
[12]	Wong, B. and Tang, K.K. (2013) Do Ageing Economies Save Less? Evidence from OECD Data. International Journal of Social Economics, 40, 591-605. https://doi.org/10.1108/03068291311321875
[13]	Harrod, R.F. (1939) An Essay in Dynamic Theory. The Economic Journal, 49, 14-33. https://doi.org/10.2307/2225181
[14]	Domar, E.D. (1946) Capital Expansion, Rate of Growth, and Employment. Econometrica, 14, 137-147. https://doi.org/10.2307/1905364
[15]	Domar, E.D. (1949) Capital Accumulation and the End of Prosperity. Econometrica, 17, 307-314. https://doi.org/10.2307/1907318
[16]	Solow, R. (1956) A Contribution to the Theory of Economic Growth. The Quarterly Journal of Economics, 70, 65-94. https://doi.org/10.2307/1884513
[17]	Becker, G.S., Murphy, K.M. and Tamura, R. (1990) Human Capital, Fertility, and Economic Growth. Journal of Political Economy, 98, S12-S37. https://doi.org/10.1086/261723
[18]	Romer, P.M. (1990) Endogenous Technological Change. Journal of Political Economy, 98, S71-S102. https://doi.org/10.1086/261725
[19]	Barro, R.J. (1991) Economic Growth in a Cross Section of Countries. The Quarterly Journal of Economics, 106, 407-443. https://doi.org/10.2307/2937943
[20]	Barro, R.J. and Lee, J.-W. (1994) Sources of Economic Growth. Carnegie-Rochester Conference Series on Public Policy, 40, 1-46. https://doi.org/10.1016/0167-2231(94)90002-7
[21]	Mankiw, N.G., Romer, D. and Weil, D.N. (1992) A Contribution to the Empirics of Economic Growth. Quarterly Journal of Economics, 107, 407-437. https://doi.org/10.2307/2118477
[22]	Jones, C.I. (1995) R&D-Based Models of Economic Growth. Journal of Political Economy, 103, 759-784. https://doi.org/10.1086/262002
[23]	Bloom, D.E., Canning, D. and Malaney, P.N. (2000) Population Dynamics and Economic Growth in Asia. Population and Development Review, 26, 257-290.
[24]	Romer, P. (1986) Increasing Returns and Long-Run Growth. Journal of Political Economy, 94, 1002-1037. https://doi.org/10.1086/261420
[25]	Lucas, R.E. (1988) On the Mechanics of Economic Development. Journal of Monetary Economics, 22, 3-42. https://doi.org/10.1016/0304-3932(88)90168-7
[26]	Rebelo, S. (1991) Long-Run Policy Analysis and Long-Run Growth. Journal of Political Economy, 99, 500-521. https://doi.org/10.1086/261764
[27]	Miller, S.M. (1988) Are Saving and Investment Co-Integrated? Economics Letters, 27, 31-34. https://doi.org/10.1016/0165-1765(88)90215-7
[28]	Kim, S. and Lee, J.-W. (2007) Demographic Changes, Saving, and Current Account in East Asia. Asian Economic Papers, 6, 22-53. https://doi.org/10.1162/asep.2007.6.2.22
[29]	Kumar Narayan, P. (2005) The Relationship between Saving and Investment for Japan. Japan and the World Economy, 17, 293-309. https://doi.org/10.1016/j.japwor.2004.02.002
[30]	Andrei, E.-A. and Huidumac-Petrescu, C.-E. (2013) Saving and Economic Growth: An Empirical Analysis for Euro Area Countries. Theoretical and Applied Economics, 20, 43-58.
[31]	Bayar, Y. (2014) Savings, Foreign Direct Investment Inflows and Economic Growth in Emerging Asian Economies. Asian Economic and Financial Review, 4, 1106-1122.
[32]	Braun, R.A., Ikeda, D. and Joines, D.H. (2009) The Saving Rate in Japan: Why It Has Fallen and Why It Will Remain Low. International Economic Review, 5, 291-321. https://doi.org/10.1111/j.1468-2354.2008.00531.x
[33]	Bloom, D.E., Canning, D. and Sevilla, J. (2003) The Demographic Dividend: A New Perspective on the Economic Consequences of Population Change. RAND Corporation, Santa Monica. https://doi.org/10.7249/MR1274 https://www.rand.org/content/dam/rand/pubs/monograph_reports/2007/MR1274.pdf