Elastic Collisions in Minkowski Momentum Space with Lorentz Transformations ()
1. Introduction
Collisions of the interacting particles have fundamental importance in both classical mechanics and special relativity. Illustrating the collision problems is rewarding to understand them clearly and quickly.
For one dimensional collision in classical mechanics, mass-momentum diagram plays a key role [1] [2]. We can see the whole story of the collision in the single diagram for both the center-of-mass and the laboratory systems. For two dimensional collision in classical mechanics, two-dimensional momentum space describes the collision clearly in the textbook [3]. We also see the slightly different illustration which lays emphasis on the transformation of the two systems [4]. For one dimensional collision in the special relativity, Saletan [5] proposed to understand the collision problems in the Minkowski momentum space, with energy E/c represented along the vertical axis and momentum p represented along the horizontal axis. The states of the particles are expressed by the arrow in the space. The quantitative application of it is stated by [6]. We do not need any calculation for obtaining the whole story of the collision. For two dimensional collision in the special relativity, illustration is clearly stated in the literature [6] [7]. We also see the slightly different illustration which lays emphasis on the transformation of the two systems [8].
In this article, we propose a different point of view for the elastic collision problems in the special relativity. We make a detour through the center-of-mass system for obtaining the final states in the laboratory system. It is applicable to both one and two dimensional collisions. This method shows the unified way to think about collision problems.
Now, consider two reference frames K and K'. We assume that the frame K' moves in the x-direction at speed V with respect to the frame K. And let us assume the origins O and O' of the two reference frames coincide at time
. An event that occurs at some point is observed from both frames and is characterized by a set of coordinates
and
where c is the speed of light. The Lorentz transformation gives the relation between two coordinates and it is described by
(1)
where
and
. In the following paper, we designate the frame K as the laboratory system, while K' as the center-of-mass system. Accordingly, the velocity V describes the velocity of the center-of-mass. The inverse transformation is given by just putting
to
in Equation (1).
Our strategy is pictorially stated in Figure 1. In the textbooks of physics, we have to calculate the simultaneous equations of momentum- and energy-conservation in order to obtain the final states in the laboratory system. See the dashed arrow in Figure 1. Our strategy is as follows.
1) By the Lorentz inverse transformation, we obtain the velocity V of the center-of-mass in terms of energies (
,
) and momenta (
,
) in the laboratory system before the collision. The velocity V does not change throughout the collision.
2) By the Lorentz transformation, we obtain the momenta (
,
) in the center-of-mass system before the collision. See the strategy 2 in Figure 1. In this frame, two particles make a head on collision with the same magnitude of the momentum
.
3) We determine the momenta (
,
) in the center-of-mass system after the collision. See the strategy 3 in Figure 1. In this frame, two particles move the opposite direction with the same momentum
after the collision. We introduce the collision angle
of the incident particle for the two dimensional case.
![]()
Figure 1. The usual approach to the collision problems is along the dashed arrow. The strategy in this article is on the detour of the solid arrows.
4) By the Lorentz inverse transformation, we obtain the momenta (
,
) in the laboratory system after the collision. See the strategy 4 in Figure 1. Finally, we reach the final states. We never solve the simultaneous equations in contrast with the usual treatment of the collision problems.
5) Let us consider the two special cases. One is that the target particle is at rest (
) in the laboratory system before the collision. The other is that, in addition to the condition above, two particles have equal masses.
6) We check the limit
and see whether these strategies recover the Newtonian mechanics.
This paper is organized in the following way. In Section 2, we discuss one dimensional collisions, according to the strategy stated above. We also show the illustration of these collisions in Minkowski momentum space. This diagram shows the whole story of the one dimensional collision in the special relativity. In Section 3, we turn to the two dimensional collision case. We introduce the collision angle
of the incident particle in the center-of-mass system. We show the theoretical background for the diagrammatic approach [6] [7] [8]. Section 4 is devoted to a summary.
2. Elastic Collisions in One Dimension
Let us discuss the one dimensional elastic collisions. The motions of the particles are restricted in the x-direction. Therefore, the y- and z-components of the momentum are zero. Although the illustrations of the contents of this section are already done by [5] [6], we reexamined how we draw the collision problems in the Minkowski momentum space.
2.1. Velocity of Center-of-Mass System
We discuss the strategy 1 in the Introduction. Consider the Lorentz inverse transformation with the whole two body system,
(2)
Here,
is the definition of the center-of-mass system. From the matrix, we obtain the following relations:
(3)
(4)
Dividing these equations, we obtain the velocity of the center-of-mass
(5)
which is conserved throughout the collision because of the conservation law of energy and momentum. Moreover, we define the following conserved quantity:
(6)
(7)
where
and
are the masses of the colliding particles. We used the relation
, which is satisfied by the relativistic particle. When we define W as the total energy in the center-of-mass system, then W is written in terms of s as follows:
(8)
We also calculate the following quantities from Equation (5),
(9)
which are frequently used in the following sections.
Figure 2 depicts the states of two particles before the collision in the laboratory system:
(10)
According to the parallelogram law, we obtain the vector
, which indicates the state of the center-of-mass. The
in Equation (5) is understood by
in Figure 2. Moreover, the vector
shows the case
![]()
Figure 2. Figure shows the case in [6] :
,
,
,
. The tips A and B show the states of the particles before the collision in the laboratory system. The tip C is determined from A and B by the parallelogram law.
of the perfect inelastic collision in the special relativity, i.e., the two particles are combined and move with the velocity
after the collision. Contrary to this, this diagram is also interpreted as the decay process. The parent particle
decays into two daughter particles
and
.
2.2. Momenta and Energies in the Center-of-Mass System before the Collision
We discuss the strategy 2 in the Introduction. Concerning the Lorentz transformation for each particle,
(11)
we obtain the momenta in the center-of-mass system before the collision;
(12)
(13)
where we used Equations (9). It is natural that
is fulfilled because of the definition of the center-of-mass system. Then we define a momentum
as
(14)
for later use. The energies of the particles in the system are also given by Equations (11),
(15)
(16)
where we used Equations (7) and (9). These energies are also derived by
and
with Equations (12) and (13). Summing up these energies, we can easily see Equation (8).
We obtain these results from Figure 3. We draw a new
-axis which has the slope
with respect to the horizontal p-axis. Drawing the dotted line from the tips A and B to the
-axis in parallel to the line OC, the crossing points indicate the momenta
and
whose distances from the origin O are equal. This means
. Moreover, we draw the dotted line from the tips A and B to the line OC in parallel to the
-axis. The crossing points A'' and B'' describe the energies
and
in the center-of-mass system before the collision.
2.3. Momenta and Energies in the Center-of-Mass System after the Collision
We discuss the strategy 3 in the Introduction. We determine the momenta in the
![]()
Figure 3. Draw the line from the tips of the vectors A and B to the
-axis in parallel to the line OC. The crossing points with
-axis show the momenta of each particle in the center-of-mass system.
center-of-mass system after the collision. In this frame, the particles move in the opposite direction after the collision with the same magnitude of
in Equation (14). We write down the momenta in the center-of-mass system after the collision
(17)
Since the magnitudes of the momenta do not change, the energies of the particles
(18)
do not change either in this frame, where
and
are given by equations (15) and (16).
2.4. Momenta and Energies in the Laboratory System after the Collision
We discuss the strategy 4 in the Introduction. Consider the Lorentz inverse transformation for each particle,
(19)
we obtain the momenta in the laboratory system after the collision. From the second row of these matrices, we obtain
(20)
(21)
where we used Equations (9), (17) and (18). Adding the two equations, we easily see the conservation of momentum:
. Moreover, we also obtain the energies from Equations (19),
(22)
(23)
where we used Equations (9), (17) and (18). We easily check the conservation of energy:
.
Figure 4 shows the whole story of the one dimensional collision. Since the momenta of the particles exchange in the center-of-mass system after the collision, the tips A and B', B and A' are on the same dotted line. Thus, the dashed vectors
(24)
show the states after the collision. Namely, the tip A(B) can slide on the hyperbola
until the tip A'(B'). Furthermore, the sum of these vectors
equals
, which means that
is not altered throughout the collision.
The point A''(B'') is the midpoint of the line AA'(BB') which means that the energies in the center-of-mass system do not change before and after the collision, i.e., Equation (18).
Once the momenta and energies of the particles before the collision are given, we obtain the final states as shown in Figure 4 without any calculations.
2.5. In Case of
We discuss the strategy 5 in the Introduction. In this case, we substitute
into the equations of this section. Equation (7) becomes simple form
![]()
Figure 4. The solid and dashed arrows show the states of the particles before and after the collision.
(25)
and we obtain the relation
(26)
From Equations (20) and (21), we obtain the momenta in the laboratory system after the collision
(27)
(28)
The second term of the right hand side of Equation (27) is a momentum lost by the particle A, and this transfers to the momentum gained by the particle B in Equation (28). This is the impulse in the special relativity. We obviously understand the conservation of the momentum:
. In addition, we obtain the energies from Equations (22) and (23)
(29)
(30)
The second terms of the right hand side of both equations are the same and it transfers from the particle A to B. This is the work in the special relativity. The
sum of these energies
shows the conservation law of energy.
Figure 5 shows the Minkowski momentum diagram in this case. The vector
is along the vertical axis, which means
before the collision.
2.6. In Case of
and
The quantity s becomes more simple form
(31)
and we obtain the following relations
(32)
We obtain the momenta
(33)
and energies
![]()
Figure 5. The solid and dashed arrows show the states of the particles before and after the collision in case of
.
(34)
in the laboratory system. After the collision, the incident particle A stops and the initially rest particle B moves with the momentum of which the particle A had before the collision.
2.7. In the Limit
In the limit
, the relativistic energy E is replaced by
. Equation (5) becomes
(35)
This is the velocity of the center-of-mass in Newtonian mechanics. Equation (7) shows
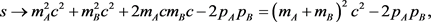 (36)
(36)
then, the Lorentz factors Equations (9) become
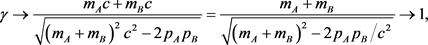
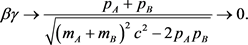
Equation (14) becomes
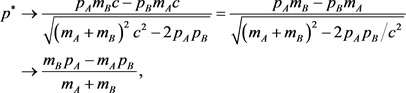 (37)
(37)
which is the momentum in the center-of-mass system in Newtonian mechanics. Using these equations, we obtain the momenta Equations (20) and (21),
 (38)
(38)
 (39)
(39)
after the collision in the laboratory system, which are recovered the case in Newtonian mechanics.
3. Elastic Collisions in Two Dimensions
Let us turn our discussion to the case of the two dimensional elastic collisions. We suppose that the motions of the particles are restricted in the x-y plain, so that the z-component of the momentum is zero. Since the motions of the particles are supposed along the x-direction before the collision, we repeat the same discussion of Subsections 2.1 and 2.2. The illustration of this section is already done by [7] [8].
3.1. Momenta and Energies in the Center-of-Mass System after the Collision
Let us start our discussion from the strategy 3 in the Introduction. In the center-of-mass system, the magnitudes of the momenta do not change before and after the collision. Thus, we write down the momenta in the same way with Equation (14),
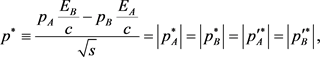 (40)
(40)
where s is defined by Equation (7).
However, the direction of the momenta changes after the collision in two dimensions. As shown in Figure 6, we define the sense of the momentum 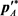 as
as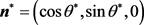 , where
, where  is the scattering angle of the particle A in the center-of-mass system. In other words, the momenta after the collisions are denoted by the vector-form:
is the scattering angle of the particle A in the center-of-mass system. In other words, the momenta after the collisions are denoted by the vector-form:
 (41)
(41)
Since the magnitudes of the momenta do not change in this frame throughout the collision, the energies of each particle do not change either:
 (42)
(42)
where  and
and ![]() are given by Equations (15) and (16).
are given by Equations (15) and (16).
3.2. Momenta and Energies in the Laboratory System after the Collision
We discuss the strategy 4 in the Introduction. The motion of the particles after the collision is supposed to occur in the x-y plain. Thus, the momenta are
written by ![]() and
and ![]() , where
, where ![]() and
and ![]() are the scattering angle of the particles A and B in the laboratory system as shown in Figure 6.
are the scattering angle of the particles A and B in the laboratory system as shown in Figure 6.
From the Lorentz inverse transformation, we obtain the momenta in the laboratory system after the collision by using Equation (41)
![]() (43)
(43)
![]() (44)
(44)
From the second and third row of these matrices, we obtain x- and y-components of the momentum for the particle A,
![]() (45)
(45)
![]() (46)
(46)
and for the particle B,
![]() (47)
(47)
![]() (48)
(48)
Combining with the relation![]() , we obtain
, we obtain
![]() (49)
(49)
![]() (50)
(50)
These equations show the ellipse with the following parameters:
![]() (51)
(51)
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
where Equations (7), (9), (14), (15) and (16) are used.
From the Lorentz transformation Equation (43) with Equation (15), we obtain the energy in the laboratory system after the collision
![]() (56)
(56)
where we used Equations (9). In the same manner, from Equations (44) and (16), we obtain
![]() (57)
(57)
The second terms of the right hand side in Equations (56) and (57) show the energy lost by the particle A and the energy gained by the particle B. This is the
work in the special relativity. From these energies, we clearly see the conservation law of the energy:![]() .
.
3.3. In Case of ![]()
We discuss the strategy 5 in the Introduction. The parameters of the ellipse become simple form:
![]() (58)
(58)
![]() (59)
(59)
![]() (60)
(60)
![]() (61)
(61)
where s is given by Equation (25). Equation (59) is as the same relation with Equation (26). The ellipse Equation (49) with these parameters is depicted in Figure 7. This is already done by [8].
3.4. In Case of ![]() and
and ![]()
The parameters of the ellipse are the followings:
![]() (62)
(62)
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
where s is given by Equation (31). Equations (63) and (65) are as same as Equation (32).
Dividing Equations (45), (46) and Equations (47), (48), we obtain the relations of the scattering angles
![]() (66)
(66)
![]() (67)
(67)
Thus the product of these two equations becomes
![]() (68)
(68)
![]()
Figure 7.The ellipse Equation (49) with ![]() is illustrated in the solid line. The points E' and E'' are the foci of this ellipse and the midpoint of them is depicted by E. The dashed circle shows the collision in the center-of-mass system [8].
is illustrated in the solid line. The points E' and E'' are the foci of this ellipse and the midpoint of them is depicted by E. The dashed circle shows the collision in the center-of-mass system [8].
Because of the relation of the tangent
![]()
we obtain![]() , in contrast to the Newtonian case in which
, in contrast to the Newtonian case in which![]() .
.
3.5. In Case of ![]() and
and![]() : Compton Scattering
: Compton Scattering
From the Lorentz inverse transformation in Equation (43), we obtain
![]() (69)
(69)
![]() (70)
(70)
Eliminating ![]() and using Equation (15), we obtain
and using Equation (15), we obtain
![]() (71)
(71)
Suppose that photon has no mass![]() , i.e.,
, i.e., ![]() and the target electron is at rest (
and the target electron is at rest (![]() ) before the collision. We rewrite Equation (5) as
) before the collision. We rewrite Equation (5) as
![]()
and substitute it into Equation (71). Thus we obtain
![]() (72)
(72)
This equation gives the photon energy after the collision. Hence, using the relation![]() , we obtain
, we obtain
![]() (73)
(73)
which is the Compton wavelength shift.
3.6. In the Limit ![]()
Using the limit of Equation (36), the parameters of the ellipse become the followings:
![]() (74)
(74)
![]() (75)
(75)
![]() (76)
(76)
![]() (77)
(77)
![]() (78)
(78)
where V is given by Equation (35). The minor and major semiaxes become the same and the eccentricity becomes zero. This shows that the ellipse approaches the circle, which recovers the Newtonian collision [3] [4] [7] [8].
4. Summary
We reexamined the elastic collision problems in the special relativity by using the detour through the center-of-mass system. Hopping to the center-of-mass system by the Lorentz transformation and jumping back to the laboratory system by the inverse transformation, we obtain the momenta and energies in the laboratory system after the collision without calculating any simultaneous equations which are often used in the literature. We also show that this process is applicable to the collisions both one and two dimensions in the same manner. This process makes students understand the collision problems in a unified way.
Acknowledgements
The author thanks the anonymous reviewer for his helpful suggestions.