Double Lipschitz Stability for Nonlinearly Perturbed Differential Systems with Multiple Delay ()
1. Introduction
In 1892, Lyapunov, a Russian mathematician, mechanician and physicist, proposed the notion of the stability of motion. He gave the general research methods in his doctoral dissertation “The general problem of the stability of motion” [1], in which he established the foundation of the stability theory. When studying nonlinear systems, especially studying dynamic systems or control systems, we cannot study the stability of all variables because of the technology difficulties, the limitation of practical conditions, or it is not necessary to study all variables considering the actual need. As a result, studying the partial stability of differential equations becomes more important. In addition, the partial stability is widely used in science and technology. For instance, the absolute stability of famous Lurie adjusting systems can be changed into a problem of partial stability. In a word, it is of practical significance to study the partial stability of differential equations.
In 1986, Dannan and Elaydi ( [2] ) introduced a new notion of stability, which is called uniform Lipschitz stability (ULS), for systems of differential equations
, (1)
where
,
,
, and
is the solution of (1) with
, where
.
This notion of ULS lies somewhere between uniform stability (US) on one side and the notions of asymptotic stability in variation (ASV) and uniform stability in variation (USV) on the other side. An important feature of ULS is that the linearized system inherits the property of ULS from the original nonlinear system.
YU-LI Fu ( [3] ) considers the system with time-delay
, (2)
where
,
,
, f is continuous,
,
,
.
Sung Kyu Choi, Ki Shik Koo and Keonhee Lee ( [4] ) investigated the problems of ULS, EAS and GEASV for the following various perturbed differential systems of the nonlinear differential system (1) and
, (3)
, (4)
where
is a continuous
matrix defined on
,
with
.
Vorotnikov, V. I. ( [5] [6] ) considered the following system
, (5)
and studied the double stability as
and
.
In this paper, the author considers a new class of the nonlinearly perturbed differential systems with time-delay
, (6)
where
,
,
,
,
,
,
,
is a non-negative constant.
It is obvious that the above system is a generalization of the systems in [2] - [6]. The aim of this paper is to investigate the double stability of time-delay differential equations, including Uniform stability and Uniform Lipschitz stability. The author uses the method of differential inequalities with time-delay and integral inequalities to establish double stability criteria.
2. Preliminaries
1) Definitions and lemmas
Consider the following system:
, (7)
where
,
,
,
,
,
is a non-negative constant. Let
be a continuous function, for
.
Definition 1: The trivial solution of system (7) has uniform stability and exponential asymptotic stability with respect to y if, for
,
,
and
, when
(for
), such that
,
, for all
.
Definition 2: The trivial solution of system (7) has Lipschitz stability with respect to y if, there exist constants
and
, when
(for
), such that
, for all
.
Definition 3: The trivial solution of system (7) has equi-exponential Lipschitz asymptotic stability with respect to y if, there exist constants
,
and
, when
(for
), such that
, for all
.
Definition 4: The trivial solution of system (7) has uniform exponential Lipschitz asymptotic stability with respect to y if, K and
in Definition3 are unrelated to
.
Lemma 1. [7] Consider the homogeneous system
, (8)
if the trivial solution of system (8) has uniform stability, and has exponential asymptotic stability with respect to y, then there exists a Lyapunov-function
satisfied the following conditions:
where
.
Consider the following inequality:
(9)
where
and
,
,
,
,
are nonnegative and not monotone decreasing for “
”,
,
,
,
,
.
Lemma 2. [8] Suppose
be nonnegative continuous on
, for all
(3) is satisfied, if
the following inequality holds:
,
,
when
, we have following result:
,
holds true, where
, and
.
2) Differential Inequalities with Time-Delay
Consider the following inequality
(10)
where
and
,
,
,
are nonnegative and not monotone ecreasing for “
”,
,
,
,
,
.
Lemma 3. Assume
be nonnegative continuous on
, (10) is satisfied for all
, there exists a constant K satisfied the following inequality:
, (11)
and
,
then if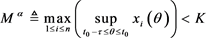 , the following inequality:
, the following inequality:
holds true, where
and
.
Proof
According to (10), for
,
(let
) we can get
Now define
thus, we can have
furthermore
(13)
Let
obviously
hence
Notice that
and
Applying (12) into (10), we have
(14)
For any scaler
, we can get
If not, then
, thus there exists a certain i in
and
, we have
thus we can get
. Using it in (14), we get
It is a contradictory, thus
, let
, we can get
Notice (12), the following is obtained
, for all
.
Remark It is obvious that when
lemma 2 can be deduced by lemma 3.
3. Main Results
Consider the following system which is equivalent with system (1)
(15)
where
,
is a constant, initial condition is:
,
,
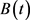 is an
is an  matrix,
matrix, 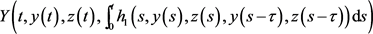 is an
is an 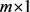 matrix,
matrix, 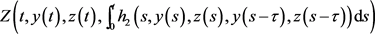 is an
is an 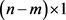 matrix, they are all continuous for
matrix, they are all continuous for 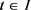 and satisfy the condition of existence and uniqueness theorem.
and satisfy the condition of existence and uniqueness theorem.
The homogeneous system of (15) is
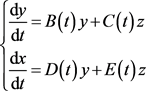 . (15)*
. (15)*
Theorem: If (15) satisfies the following conditions:
1)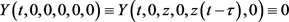 .
.
2) .
.
3)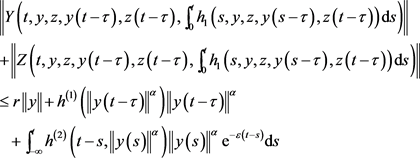 .
.
where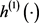 ,
,  are nonnegative and not monotone decreasing for “
are nonnegative and not monotone decreasing for “ ”,
”,  , and
, and
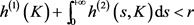 ,
, 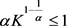 ,
,
then the trivial solution of system (15) has uniform exponential Lipschitz asymptotic stability with respect to y, when the trivial solution of system (15)* has uniform stability and exponential asymptotic stability with respect to y.
Proof The V-Ляпунов function of (15)*, which is obtained under the condition of theorem, satisfies following conditions:
![]() ,
, ![]() , (16)
, (16)
![]() , (
, (![]() ), (17)
), (17)
for![]() ,
,![]() .
.
Derivative the V-Ляпунов function ![]() along (15), we get
along (15), we get
![]() ,
,
where
![]()
![]()
here ![]() the notation of inner product.
the notation of inner product.
From condition of theorem and (17), when ![]() we have
we have
![]()
By the first inequality of (16), the above can be expressed as follow:
![]()
then there exists ![]() such that when
such that when ![]() and
and ![]() , we get
, we get
![]() ,
,
here select the appropriate small constant r such that
![]() and
and![]() ,
,
hence by the lemma [9] [10], there exists ![]() such that for all
such that for all ![]() we have
we have
![]() . (18)
. (18)
For any solution of (15), from the inequality (18) and the first inequality of (16) we obtain
![]() .
.
According to the proof of the theorem in [11], we get![]() , hence we obtain that the trivial solution of system (15) has uniform stability and uniform exponential Lipschitz asymptotic stability with respect to y.
, hence we obtain that the trivial solution of system (15) has uniform stability and uniform exponential Lipschitz asymptotic stability with respect to y.
4. Conclusion
In this paper, we use the method of differential inequalities with time-delay and integral inequalities to establish double stability criteria. As a result, studying the partial stability of differential equations becomes more important. In addition, the partial stability of differential equations is widely used in science and technology.
Acknowledgements
The authors are grateful to Professor Si Ligeng and the referee for several helpful comments.
Supported
Supported by Inner Mongolia Autonomous Region Higher Education Research Project (No.NJZY17064, NJZY16141).