The Approach to Probabilistic Decision-Theoretic Rough Set in Intuitionistic Fuzzy Information Systems

Binbin Sang^1,2, Xiaoyan Zhang^1,3*

¹School of Science, Chongqing University of Technology, Chongqing, China.
²School of Information Science and Technology, Southwest Jiaotong University, Chengdu, China.
³College of Artificial Intelligence, Southwest University, Chongqing, China.

DOI: 10.4236/iim.2020.121001                

Abstract

For the moment, the representative and hot research is decision-theoretic rough set (DTRS) which provides a new viewpoint to deal with decision-making problems under risk and uncertainty, and has been applied in many fields. Based on rough set theory, Yao proposed the three-way decision theory which is a prolongation of the classical two-way decision approach. This paper investigates the probabilistic DTRS in the framework of intuitionistic fuzzy information system (IFIS). Firstly, based on IFIS, this paper constructs fuzzy approximate spaces and intuitionistic fuzzy (IF) approximate spaces by defining fuzzy equivalence relation and IF equivalence relation, respectively. And the fuzzy probabilistic spaces and IF probabilistic spaces are based on fuzzy approximate spaces and IF approximate spaces, respectively. Thus, the fuzzy probabilistic approximate spaces and the IF probabilistic approximate spaces are constructed, respectively. Then, based on the three-way decision theory, this paper structures DTRS approach model on fuzzy probabilistic approximate spaces and IF probabilistic approximate spaces, respectively. So, the fuzzy decision-theoretic rough set (FDTRS) model and the intuitionistic fuzzy decision-theoretic rough set (IFDTRS) model are constructed on fuzzy probabilistic approximate spaces and IF probabilistic approximate spaces, respectively. Finally, based on the above DTRS model, some illustrative examples about the risk investment of projects are introduced to make decision analysis. Furthermore, the effectiveness of this method is verified.

Keywords

Fuzzy Decision-Theoretic Rough Set, Intuitionistic Fuzzy Information Systems, Intuitionistic Fuzzy Decision-Theoretic Rough Set, Probabilistic Approximate Spaces

1. Introduction

Rough set [1] is a kind of theory of dealing with imprecise and incomplete data by Poland mathematician Pawlak. It is a significant mathematic tool in the areas of data mining [2] and decision theory [3]. Compared with the classical set theory, rough set theory does not require any transcendental knowledge about data, such as membership function of fuzzy set or probability distribution. Pawlak mainly based on the object between the indistinguishability of the theory of object clustering into basic knowledge domain, by using the basic knowledge of the upper and lower approximation [4] to describe the data object uncertainty, which derives the concept of classification or decision rule. Related researches spread many field, for instance, machine learning [5] - [10], cloud computing [11] [12] [13] [14], knowledge discovery [15] [16] [17] [18], biological information processing [19] [20], artificial intelligence [21] [22] [23] [24] [25], neural computing [26] [27] [28] and so on.

The concept of intuitionistic fuzzy set theory [29] was proposed by Atanassov in 1986. As a generalization of fuzzy set, the concept of IF set has been successfully applied in many field for data analysis [30] [31] [32] and pattern recognition [33] [34]. IF set is compatible with the three aspects of membership and non membership and hesitation. Therefore, IF sets are more comprehensive and practical than the traditional fuzzy sets in dealing with vagueness and uncertainty. Combing IF set theory and rough set theory may result in a new hybrid mathematical structure [35] [36] for the requirement of knowledge-handling system. Studies of the combination of information system and IF set theory are being accepted as a vigorous research direction to rough set theory. Based on intuitionistic fuzzy information system [37], a large amount of researchers focused on the theory of IF set. Recently, Zhang et al. [38] defined two new dominance relations and obtained two generalized dominance rough set models according to defining the overall evaluations and adding particular requirements for some individual attributes. Meanwhile, the attribute reductions of dominance IF decision information systems are also examined with these two models. Zhong et al. [39] extended the TOPSIS (technique for order performance by similarity to an ideal solution) approach to deal with hybrid IF information. Feng et al. [40] studied probability problems of IF sets and the belief structure of general IFIS. Xu et al. [41] investigated the definite integrals of multiplicative IFIS in decision making. Furthermore, they studied the forms of indefinite integrals, deduced the fundamental theorem of calculus, derived the concrete formulas for ease of calculating definite integrals from different angles, and discussed some useful properties of the proposed definite integrals.

As we all know, the Pawlak algebra rough set model is used to simulate the concept granulation ability and the concept approximation ability of human intelligence. The algebraic inclusion relation between concept and granule is the theoretical basis of the simulation. However, there is an obvious deficiency in the simulation of human intelligence in terms of the fault tolerance of simulated human intelligence. To solve this problem, many researchers have proposed a decision rough set model. The DTRS have established the decisions rough set model with noise tolerance mechanism, which defines concept boundaries make Bayes risk decision method [42] [43]. The concept of DTRS three decision includes positive region, boundary region and negative region. Positive region determine acceptance. Negative region determine reject, and bounds region are to make decision of deferment. As an stretch of the Pawlak’s rough set model, it has been extraordinarily popular in varieties of practical and theoretical fields, for instance, expanded his research in the field of rough set theory [44] [45] [46] [47] and information filtering [48] [49] [50], risk decision analysis [51], cluster analysis and text classification [52], network support system and game analysis [53]. Recently, DTRS has been paid more and more attention. Zhou et al. [50] introduced a three-way decision approach to filter spam based on Bayesian decision theory, Li et al. [54] presented a full description on diverse decisions according to different risk bias of decision makers, and Liu et al. [55] emphasized on the semantic studies on investment problems. Liu chose the topgallant action with maximum conditional profit. A pair of a cost function and a revenue function is used to calculate the two thresholds automatically. On the other hand, Xu et al. [3] studied two kinds of generalized multigranulation double-quantitative DTRS by considering relative and absolute quantitative information, Yao et al. [56] [57] [58] provided a formal description of this method within the framework of probabilistic rough sets, and Liu et al. [59] studied the semantics of loss functions, and exploited the differences of losses replace actual losses to construct a new “four-level” approach of probabilistic rules choosing criteria. Furthermore, Yang et al. [60] proposed a fuzzy probabilistic rough set model on two universes. Although they have discussed fuzzy relation in their paper, it is the λ-cut sets of fuzzy relation replaced the fuzzy relation itself that works when computing the conditional probability [61] [62] [63]. Sun et al. [64] presented a decision-theoretic rough fuzzy set. That is, they structured a non-parametric definition of the probabilistic rough fuzzy set.

However, these DTRS models have just discussed the classical equivalence relations. Thus, IFIS data make them more difficulty to function. Such as, when dealing with a IFIS data, the fuzzy equivalence relation or IF equivalence relation obtained from data should be first transformed into classical equivalence relation in case of computing probability. This is complicated, and this may cause information loss for improper λ. In order to accurately deal with IFIS data, we transmute IFIS into fuzzy approximate space and IF approximate space by fuzzy equivalence relation and IF equivalence relation respectively. By considering fuzzy probability and IF probability, the fuzzy probabilistic approximate spaces and the IF probabilistic approximate spaces are constructed, respectively. Then, DTRS model has been established in fuzzy probabilistic approximate space and IF probabilistic approximate space, respectively. Consequently, we can conduct decision analysis on IFIS data by the proposed FDTRS model and IFDTRS model, respectively. This is the main work of this paper.

The rest of this paper is organized as follows. Section 2 provides the basic concept of fuzzy set, fuzzy relation, fuzzy probability, IF set, IFIS etc. In Section 3, we construct fuzzy approximate spaces by defining fuzzy equivalence relation. By considering fuzzy probability, we propose FDTRS model in fuzzy probabilistic approximate space. The effectiveness of the model is proved by a case. In Section 4, we construct IF probabilistic approximate spaces by defined IF equivalence relation. By considering IF probability, we propose IFDTRS model in IF probabilistic approximate space. Besides, we generalize the loss function λ. The effectiveness of the model is proved by a case. At last, we conclude our research and suggest further research directions in Section 5.

2. Preliminaries

For more convenience, this section recalls some basic concepts of fuzzy set, fuzzy relation, fuzzy probability, intuitionistic fuzzy sets, intuitionistic fuzzy information system etc. More details can be found in [29] [40] [65] [66] [67].

2.1. Fuzzy Set, Fuzzy Relation and Fuzzy Probability

Definition 2.1.1 [65] Let U be a universe of discourse

$A\mathrm{<mo>\; :\; </mo>}U\to \left[\mathrm{0,1}\right]$

$u|\to A(x)$

then A is called fuzzy set on U. $A\left(x\right)$ is called the membership function of A.

The family of all fuzzy sets on U is denoted by $F\left(U\right)$ . Let $A\mathrm{,}B\in F\left(U\right)$ . Related operations of fuzzy sets.

1) $\forall x\in U$ , $B\left(x\right)\le A\left(x\right)\Rightarrow B\subseteq A$ .

2) $\left(A\cup B\right)\left(x\right)=A\left(x\right)\vee B\left(x\right)=\max \left(A\left(x\right)\mathrm{,}B\left(x\right)\right)$ ; $\left(A\cap B\right)\left(x\right)=A\left(x\right)\wedge B\left(x\right)=\min \left(A\left(x\right)\mathrm{,}B\left(x\right)\right)$ .

3) $\left(AB\right)\left(x\right)=A\left(x\right)B\left(x\right)$ , $A^c\left(x\right)=1-A\left(x\right)$ .

Definition 2.1.1 [66] Let R is a fuzzy relation, we say that

1) R is referred to as a reflexive relation if for any $x\in U$ , $R\left(x,x\right)=1$ .

2) R is referred to as a symmetric relation if for any $x\mathrm{,}y\in U$ , $R\left(x,y\right)=R\left(y,x\right)$ .

3) R is referred to as a transitive relation if for any $x\mathrm{,}y\mathrm{,}z\in U$ , $R\left(x\mathrm{,}y\right)\ge {\vee }_{z\in U}\left(R\left(x\mathrm{,}z\right)\wedge R\left(z\mathrm{,}y\right)\right)$ .

If R is reflexive, symmetric and transitive on U, then we say that R is a fuzzy equivalence relation on U.

Definition 2.1.2 [67] Let $\left(U\mathrm{,}A\mathrm{,}P\right)$ be a probability space. Where $A$ is the family of all fuzzy sets that is denoted by $F\left(U\right)$ . Then $A\in A$ is a fuzzy event on U. The probability of A is

$P\left(A\right)\triangleq {\displaystyle {\int }_U}A\left(x\right)\text{d}P.$

If U is a finite set, $U=\left\{x_i|i=1,2,\cdots ,n\right\}$ , $P\left(x_i\right)=p_i$ , then

$P\left(A\right)\triangleq {\displaystyle \underset{i=1}{\overset{n}{\sum }}}A\left(x_i\right)p_i$

Proposition 2.1.1 Let $\left(U\mathrm{,}A\mathrm{,}P\right)$ be a probability space $A\mathrm{,}B\in A$ . The property of the establishment.

1) $P\left(U\right)=1$ ,that is $P\left(U\right)={\displaystyle {\int }_U}\text{d}P=1$ ;

2) $0\le P\left(A\right)\le 1$ ;

3) $A\subseteq B\mathrm{,}P\left(A\right)\le P\left(B\right)$ ;

4) $P\left(A^c\right)=1-P\left(A\right)$ ;

5) $P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)$ ;

6) $P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)\mathrm{,}A\cap B=\varnothing$ .

Definition 2.1.3 [67] Let $\left(U\mathrm{,}A\mathrm{,}P\right)$ be a probability space and $A\mathrm{,}B$ be two fuzzy events on U. If $P\left(B\right)\ne 0$ then

$P\left(A\mathrm{<mo>\; |\; </mo>}B\right)=\frac{P\left(AB\right)}{P(B)}$

is called the conditional probability of A given B.

Proposition 2.1.2 Let $\left(U\mathrm{,}A\mathrm{,}P\right)$ be a probability space and A be a classical event on X. Then, for each fuzzy event B on X, it holds that

$P\left(A|B\right)+P\left(A^c|B\right)=1$

Proof.

$\begin{array}{c}P\left(A|B\right)+P\left(A^c|B\right)=\frac{P\left(AB\right)}{P\left(B\right)}+\frac{P\left(A^{c}B\right)}{P\left(B\right)}\\ =\frac{{\displaystyle {\int }_U}A\left(x\right)B\left(x\right)\text{d}P}{{\displaystyle {\int }_U}B\left(x\right)\text{d}P}+\frac{{\displaystyle {\int }_U}{A}^c\left(x\right)B\left(x\right)\text{d}P}{{\displaystyle {\int }_U}B\left(x\right)\text{d}P}\\ =\frac{{\displaystyle {\int }_A}B\left(x\right)\text{d}P+{\displaystyle {\int }_A^c}B\left(x\right)\text{d}P}{{\displaystyle {\int }_U}B\left(x\right)\text{d}P}\\ =\frac{{\displaystyle {\int }_A}\cup A^{c}B\left(x\right)\text{d}P}{{\displaystyle {\int }_U}B\left(x\right)\text{d}P}=1\end{array}$

2.2. IF relation, IF Information System and IF Probability

Definition 2.2.1 [29] Let X be a non empty classic set. The three reorganization in X like $A=\left\{\langle x\mathrm{,}{\mu }_A\left(x\right)\mathrm{,}{\nu }_A\left(x\right)\rangle |x\in X\right\}$ meets the following three points.

1) ${\mu }_A\to \left[\mathrm{0,1}\right]$ indicates that the element of X belongs to the A membership degree.

2) ${\nu }_A\to \left[\mathrm{0,1}\right]$ indicates that the non membership degree.

3) $0\le A\left(x\right)+{\nu }_A\left(x\right)\le 1$ .

A is called an intuitionistic fuzzy set on the X.

Related operations of IF sets. Suppose

$A=\left\{\langle x\mathrm{,}{\mu }_A\left(x\right)\mathrm{,}{\nu }_A\left(x\right)\rangle \mathrm{<mo>\; |\; </mo>}x\in X\right\}\in IF\left(X\right)$ ,

$B=\left\{\langle x\mathrm{,}{\mu }_B\left(x\right)\mathrm{,}{\nu }_B\left(x\right)\rangle \mathrm{<mo>\; |\; </mo>}x\in X\right\}\in IF\left(X\right)$ .

$A\subseteq B\iff {\mu }_A\left(x\right)\le {\mu }_B\left(x\right)\text{and}{\nu }_A\left(x\right)\ge {\nu }_B\left(x\right),\forall x\in X;$

$A\cap B=\left\{\langle x,\min \left\{{\mu }_A\left(x\right),{\mu }_B\left(x\right)\right\},\max \left\{{\nu }_A\left(x\right),{\nu }_B\left(x\right)\right\}\rangle |x\in X\right\};$

$A\cup B=\left\{\langle x,\max \left\{{\mu }_A\left(x\right),{\mu }_B\left(x\right)\right\},\min \left\{{\nu }_A\left(x\right),{\nu }_B\left(x\right)\right\}\rangle |x\in X\right\};$

$A^c=\left\{\langle x\mathrm{,}{\nu }_A\left(x\right)\mathrm{,}{\mu }_A\left(x\right)\rangle \mathrm{<mo>\; |\; </mo>}x\in X\right\}\mathrm{.}$

Definition 2.2.2 An intuitionistic fuzzy relation $R$ on a non-empty set X is a mapping $R\mathrm{<mo>\; :\; </mo>}X\times X\Rightarrow L$ defined as $R\left(x\mathrm{,}y\right)=\langle {\mu }_R\left(x\mathrm{,}y\right)\mathrm{,}{\nu }_R\left(x\mathrm{,}y\right)\rangle \in L$ For $x\mathrm{,}y\in X$ .The family of all IF relations on X is denoted by $R$ . An IF relation $R\in R$ is:

1) Reflexive, if $R\left(x\mathrm{,}x\right)=1$ for each $x\in X$ ;

2) Symmetric, if $R\left(x\mathrm{,}y\right)=R\left(y\mathrm{,}x\right)$ for each $x\mathrm{,}y\in X$ ;

3) Transitive, if ${\vee }_{y\in X}\left(R\left(x\mathrm{,}y\right)\wedge R\left(y\mathrm{,}z\right)\right){\le }_{L}R\left(x\mathrm{,}z\right)$ for each $x\mathrm{,}y\mathrm{,}z\in X$ .

We write the IF relation $R\left(x\mathrm{,}y\right)=\left({\mu }_R\left(x\mathrm{,}y\right)\mathrm{,}{\nu }_R\left(x\mathrm{,}y\right)\right)$ for simplicity, where ${\mu }_R\left(x\mathrm{,}y\right)\mathrm{,}{\nu }_R\left(x\mathrm{,}y\right)\mathrm{<mo>\; :\; </mo>}X\times X\to I=\left[\mathrm{0,1}\right]$ and satisfy ${\mu }_R\left(x\mathrm{,}y\right)+{\nu }_R\left(x\mathrm{,}y\right)\le \mathrm{1,}\forall x\mathrm{,}y\in X$ .

If $X=\left\{x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right\}$ is a finite set, then an IF relation $R\mathrm{<mo>\; :\; </mo>}X\times X\to L$ can be represented by an IF matrix form $R={\left(R\left(x_i\mathrm{,}{x}_j\right)\right)}_{n\times n}$ , i.e. Then

$R=\left(\begin{array}{cccc}\left({\mu }_R\left(x_1\mathrm{,}{x}_1\right)\mathrm{,}{\nu }_R\left(x_1\mathrm{,}{x}_1\right)\right)& \left({\mu }_R\left(x_1\mathrm{,}{x}_2\right)\mathrm{,}{\nu }_R\left(x_1\mathrm{,}{x}_2\right)\right)& \cdots & \left({\mu }_R\left(x_1\mathrm{,}{x}_n\right)\mathrm{,}{\nu }_R\left(x_1\mathrm{,}{x}_n\right)\right)\\ \left({\mu }_R\left(x_2\mathrm{,}{x}_1\right)\mathrm{,}{\nu }_R\left(x_2\mathrm{,}{x}_1\right)\right)& \left({\mu }_R\left(x_2\mathrm{,}{x}_2\right)\mathrm{,}{\nu }_R\left(x_2\mathrm{,}{x}_2\right)\right)& \cdots & \left({\mu }_R\left(x_2\mathrm{,}{x}_n\right)\mathrm{,}{\nu }_R\left(x_2\mathrm{,}{x}_n\right)\right)\\ ⋮& ⋮& \ddots & ⋮\\ \left({\mu }_R\left(x_n\mathrm{,}{x}_1\right)\mathrm{,}{\nu }_R\left(x_n\mathrm{,}{x}_1\right)\right)& \left({\mu }_R\left(x_n\mathrm{,}{x}_2\right)\mathrm{,}{\nu }_R\left(x_n\mathrm{,}{x}_2\right)\right)& \cdots & \left({\mu }_R\left(x_n\mathrm{,}{x}_n\right)\mathrm{,}{\nu }_R\left(x_n\mathrm{,}{x}_n\right)\right)\end{array}\right)\mathrm{.}$

$V\left(R\right)$ is the collection of IFVs $R\left(x_i\mathrm{,}{x}_j\right)$ for $i\mathrm{,}j=\mathrm{1,2,}\cdots \mathrm{,}n$ , i.e. $V\left(R\right)=\left\{\alpha \mathrm{<mo>\; |\; </mo>}\alpha =R\left(x_i\mathrm{,}{x}_j\right)\text{forsome}i\mathrm{,}j=\mathrm{1,2,}\cdots \mathrm{,}n\right\}$

Definition 2.2.3 [40] An IF information system is an ordered quadruple $I=\left(U\mathrm{,}AT\mathrm{,}V\mathrm{,}f\right)$ .

$U=\left\{x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right\}$ is a non-empty finite set of objects;

$AT=\left\{a_1\mathrm{,}{a}_2\mathrm{,}\cdots \mathrm{,}{a}_p\right\}$ is a non-empty finite set of attributes;

$V={\displaystyle \underset{a\in AT}{\cup }}{V}_a$ and $V_a$ is a domain of attribute a;

$f\mathrm{<mo>\; :\; </mo>}U\times AT\Rightarrow V$ is a function such that $f\left(x\mathrm{,}a\right)\in V_a$ , for each $a\in AT\mathrm{,}x\in U$ , called an information function, where $V_a$ is an IF set of universe U. That is $f\left(x\mathrm{,}a\right)=\langle {\mu }_a\left(x\right)\mathrm{,}{\nu }_a\left(x\right)\rangle$ , for all $a\in AT$ .

Definition 2.2.4 Let $\left(U\mathrm{,}\tilde{A}\mathrm{,}P\right)$ be a IF probability space. Where $\tilde{A}$ is the family of all IF sets that is denoted by $F\left(U\right)$ . Then $A\in \tilde{A}$ is a IF event on U. The probability of A is

$P\left(A\right)={\displaystyle {\int }_U}A\left(x\right)\text{d}P=\langle {\displaystyle {\int }_U}{\mu }_A\left(x\right)\text{d}P,{\displaystyle {\int }_U}{\nu }_A\left(x\right)\text{d}P\rangle =\langle P\left({\mu }_A\right),P\left({\nu }_A\right)\rangle .$

Among $P\left({\mu }_A\right)$ is probability of membership, $P\left({\nu }_A\right)$ is probability of nonmembership.

Proposition 2.2.1 Each IF event A is associated with an IF probability $P\left(A\right)$ . The $P$ is called an IF probability measure on U which is generated by P. If A degenerates into a classical event or a fuzzy event $A^{\prime }$ it follows that $P\left(A\right)=P\left(A^{\prime }\right)$ .

Proposition 2.2.2 Also, if $U=\left\{x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right\}$ is a finite set and $p_i=P\left(x_i\right)$ , then

$P\left(A\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}}A\left(x_i\right)p_i=\langle {\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\mu }_A\left(x_i\right)p_i,{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\nu }_A\left(x_i\right)p_i\rangle .$

Definition 2.2.4 Let $\left(U\mathrm{,}A\mathrm{,}P\right)$ be a probability space and $A\mathrm{,}B$ be two IF events on U. If $P\left({\nu }_B\right)\ne 0$ and $P\left({\mu }_B\right)\ne 0$ then

$P\left(A\mathrm{<mo>\; |\; </mo>}B\right)=\left(P\left({\mu }_A\mathrm{<mo>\; |\; </mo>}{\mu }_B\right)\mathrm{,}P\left({\nu }_A\mathrm{<mo>\; |\; </mo>}{\nu }_B\right)\right)\mathrm{.}$

is called the IF conditional probability of A given B.

2.3. Decision-Theoretic Rough Sets

Decision-theoretic rough sets were first proposed by Yao [42] for the Bayesian decision process. Based on the thoughts of three-way decisions, DTRS adopt two state sets and three action sets to depict the decision-making process. The state set is denoted by $\Omega =\left\{X\mathrm{,}{X}^c\right\}$ showing that an object belongs to X and is outside X, respectively. The action sets with respect to a state are given by $A=\left\{a_P,a_B,a_N\right\}$ , where $a_P$ , $a_B$ and $a_N$ represent three actions about deciding $x\in POS\left(X\right)$ , $x\in BND\left(X\right)$ , and $x\in NEG\left(X\right)$ , namely an object x belongs to X, is uncertain and not in X, respectively. The loss function concerning the loss of expected by taking various actions in the different states is given by the $3\times 2$ matrix in Table 1.

In Table 1, ${\lambda }_{PP}$ , ${\lambda }_{BP}$ and ${\lambda }_{NP}$ express the losses happened for taking actions of $a_P$ , $a_B$ and $a_N$ , respectively, when an object belongs to X. Similarly, ${\lambda }_{PN}$ , ${\lambda }_{BN}$ and ${\lambda }_{NN}$ indicate the losses incurred for taking the same actions when the object does not belong to X. For an object x, the expected loss on taking the actions could be expressed as:

$R\left(a_P|{\left[x\right]}_R\right)={\lambda }_{PP}P\left(X|{\left[x\right]}_R\right)+{\lambda }_{PN}P\left(X^c|{\left[x\right]}_R\right);$ (1)

$R\left(a_B|{\left[x\right]}_R\right)={\lambda }_{BP}P\left(X|{\left[x\right]}_R\right)+{\lambda }_{BN}P\left(X^c|{\left[x\right]}_R\right);$ (2)

Table 1. The cost function ${\left[\lambda \right]}_X$ for X.

$R\left(a_N|{\left[x\right]}_R\right)={\lambda }_{NP}P\left(X|{\left[x\right]}_R\right)+{\lambda }_{NN}P\left(X^c|{\left[x\right]}_R\right).$ (3)

By the Bayesian decision process, we can get the following minimum-risk decision rules:

(P) If $R\left(a_P|{\left[x\right]}_R\right)\le R\left(a_B|{\left[x\right]}_R\right)$ and $R\left(a_P|{\left[x\right]}_R\right)\le R\left(a_N|{\left[x\right]}_R\right)$ , then decide $x\in POS\left(X\right)$ ;

(B) If $R\left(a_B|{\left[x\right]}_R\right)\le R\left(a_P|{\left[x\right]}_R\right)$ and $R\left(a_B|{\left[x\right]}_R\right)\le R\left(a_N|{\left[x\right]}_R\right)$ , then decide $x\in BND\left(X\right)$ ;

(N) If $R\left(a_N|{\left[x\right]}_R\right)\le R\left(a_P|{\left[x\right]}_R\right)$ and $R\left(a_N|{\left[x\right]}_R\right)\le R\left(a_B|{\left[x\right]}_R\right)$ , then decide $x\in NEG\left(X\right)$ .

In addition, By taking into account the loss of receiving the right things is not greater than the latency, and both of them are less than the loss of refusing the accurate things; at the same time, the loss of rejecting improper things is less than or equal to the delation in accepting the correct things, and both shall be smaller than the loss of receiving the invalidate things. Hence, a reasonable assumption is that $0\le {\lambda }_{PP}\le {\lambda }_{BP}<{\lambda }_{NP}$ and $0\le {\lambda }_{NN}\le {\lambda }_{BN}<{\lambda }_{PN}$ .

Accordingly, the conditions of the three decision rules (P)-(N) are reducible to the following form.

(P) If $P\left(X|{\left[x\right]}_R\right)\ge \alpha$ and $P\left(X|{\left[x\right]}_R\right)\ge \gamma$ , then decide $x\in POS\left(X\right)$ ;

(B) If $P\left(X|{\left[x\right]}_R\right)\le \alpha$ and $P\left(X|{\left[x\right]}_R\right)\ge \beta$ , then decide $x\in BND\left(X\right)$ ;

(N) If $P\left(X|{\left[x\right]}_R\right)\ge \beta$ and $P\left(X|{\left[x\right]}_R\right)\le \gamma$ , then decide.

where the thresholds values are given by:

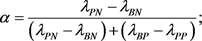
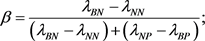
3. Decision-Theoretic Rough Set Based on Fuzzy Probability Approximation Space

In previous IF information systems, decision making often considers only the relationships among objects under individual attributes, which often leads to lack of accuracy. On this basis, the fuzzy equivalence relation is used to synthetically consider the relationship among objects under multiple attributes, and then the fuzzy approximate space is obtained. Making use of decision theory in fuzzy approximate space to analyze the data reasonably.

3.1. Fuzzy Probability Approximation Space

Definition 3.1.1 Let 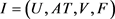be an IF information system, 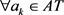, , 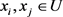, , 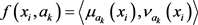then

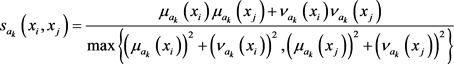
is called the relative similarity degree of and; or

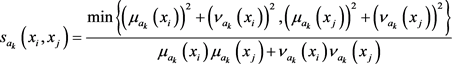
is regarded as the relative similarity degree of 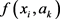and.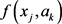

From the above two formulas, the relative similarity degree of 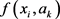and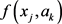, that is the similarity of objects and under the attribute. In addition, the greater the value of, the greater the similarity degree. Particularly, when, then IF number is completely similar to. In other words, the property value of objects and are identical.

Proposition 3.1.1 For any three IF numbers, , , the following properties can be obtained:

1) is bounded,;

2) is reflexive,;

3) is symmetric,;

4) is transitive, if and, then;

5) is contiguous, if is closer to than, then; if is closer to than, then.

Definition 3.1.2 Let be an IF information system, , , , . The similarity degree of objects and under attribute set AT is as follows:

Through establishing analogical relations, we could turn IF information system into a fuzzy approximation space in accordance with definition 3.1 and 3.2. The subscript AT will be omitted in the rear. It holds:

1) Firstly, U is a non-empty classical set, a binary relation R from U to U indicates a fuzzy set. So R is a fuzzy relation on the universe U.

2) Furthermore, R is a fuzzy equivalence relation on U. The reasons are as follows:

• , , R is reflexive;

• , , R is symmetric;

• , , R is transitive

These three conditions are very obvious. Therefore, ordered pair is a fuzzy approximation space.

Given the probability P with its description R, a fuzzy probability approximation space is constructed in which U is a domain of discourse, R is a fuzzy equivalence relation on U, and P is fuzzy probability of U.

3.2. Decision-Theoretic Rough Set Based on Fuzzy Probability Approximation Space

Assume be a fuzzy probability approximation space, for each, is denoted by for any. In light of (1)~(3), thus, the expected costs of adopting various actions in different states for x are expressed as follows:

(4)

(5)

(6)

Proposition 3.2.1 The condition probability and are calculated by:

(7)

(8)

In the above equations,. The computing method of condition probability is not the same as we know before. Since for every. Thus, (4) - (6) is further expressed as:

(9)

(10)

(11)

Loss function to meet the conditions: and. According to Bayesian decision process, the decision rules can be characterized by the following form:

(P₁) If and, then decide;

(B₁) If and, then decide;

(N₁) If and, then decide.

The decision rules (P₁)-(N₁) are the three-way decisions, which have three regions:, and. These rules mainly relies on the comparisons among, and which are essentially computing the fuzzy probabilities. Decision rules (P₁)-(N₁) of three-way decisions can be simplified as:

(P₂) If and, then decide;

(B₂) If and, then decide;

(N₂) If and, then decide.

Proposition 3.2.2 In this case, we have the following simplified fuzzy probability region:

In the fuzzy relation R, the fuzzy probability upper approximation and the fuzzy probability of X are respectively:

Under the discussions in Proposition3.2.2, the additional conditions of decision rule (B₂) suggest that, namely, it follows that, the rules are:

(P₃) If, then decide;

(B₃) If, then decide;

(N₃) If, then decide.

Proposition 3.2.3 In this case, we have the following simplified fuzzy probability regions:

In the fuzzy relation R, the fuzzy probability lower approximation and the fuzzy probability upper approximation of X are respectively:

According to decision-theoretic rough set, suppose the loss function satisfies, and , then we can get . Meanwhile, this paper also discusses the relationship between the value of and 1.

Case 1: When, the loss function must satisfies ;

Case 2: When, the loss function must satisfies ;

Case 3: When, the loss function must satisfies .

3.3. Case Study

Set 10 investment objects, from the perspective of risk factors for their assessment, risk factors for 5 categories: market risk, technical risk, management risk, environmental risk and production risk. Table 2 is the risk assessment form of investment, among, A = {market risk, technology risk, management risk, environment risk, production risk}. For simplicity and without loss of generality, using said the market risk, technology risk, management risk, environment risk, production risk.

Any one of the IF numbers in Table 2 is among. indicates the degree of risk under the attribute. indicates the degree of insurance under the attribute.

On the basis of Table 2, the hypothesis is a fuzzy probability approximation space, including, R is a fuzzy relation, and the fuzzy relation on U as shown in Table 3. Now assume that the preference probability distribution on U is, , , , , , , , ,. Let denotes a decision class in which the classes are excellent. In the Bayesian decision process, some experts will provide values of the loss function for X, i.e.. It exhibits three cases in Table 4. Consider the loss function of Table 4, there are .

Table 2. The IF information system of venture capital.

Table 3. A fuzzy relation on U.

Table 4. Three cases of loss function.

And the fuzzy conditional probabilities for every are computed as follows (by Equations. (7)):

, , ,

, , ,

, ,

,.

Case 1: When, namely, , it follows that,.

And

, ,

.

Based on these achievements, we can get the corresponding decision rules as follows:

(P₁) The investors most probably choose this scheme with a possibility not less than 0.54;

(B₁) The investors are less likely to invest in terms of the current conditions;

(N₁) We are not sure for who need further investigation.

Case 2: When, namely, , it follows that

,.

And

, ,

.

According to the calculation results, the decision rules in case 2 can present as follows:

(P₂) The investors most probably choose this scheme with a possibility not less than 0.5;

(B₂) The investors are less likely to invest with respect the given conditions and loss function;

(N₂) We are not sure for who need further investigation.

Case 3: When, namely, , it follows that

,.

And

, ,

.

Analogously, we can get the rest of the decision rules associate with these rough regions, as follows:

(P₃) The investors most probably choose this scheme with a possibility not less than 0.59;

(B₃) The investors are less likely to invest in terms of the given conditions and loss function;

(N₃) We are not sure for who need further investigation under the current conditions.

4. Decision-Theoretic Based on IF Probability Information System

In this section, IF relation is constructed in IF information system, and the relation between object and attribute is transformed into two relation between object and object that is. The probability of each object is given by analyzing the object, and then an IF probability approximation space is obtained. Finally, in the IF probability approximation space, the decision theory is used to analyze the decision making of IF information system.

4.1. IF Probability Approximation Space

Definition 4.1.1 Let be an IF information system, , , , , then

are called the degree of membership similarity and the degree of nonmembership similarity of and.

The similarity degree of objects and under attribute set AT is as follows:

Through establishing analogical relations, we could turn IF information system into a IF approximation space in accordance with Definition 4.1. The subscript AT will be omitted in the rear. It holds:

1) Firstly, U is a non-empty classical set, a IF relation from U to U indicates a IF set. So is a IF relation on the universe U.

2) Furthermore, is a IF equivalence relation on U. The reasons are as follows:

• , , is reflexive;

• , , is symmetric;

• , , is transitive.

These three conditions are very obvious. Therefore, ordered pair is a IF approximation space.

Given the probability with its description, a IF probability approximation space is constructed in which U is a domain of discourse, is a IF equivalence relation on U, and is fuzzy probability of U.

4.2. Decision-Theoretic Rough Set Based on IF Probability Approximation Space

Let be a IF information system and P be a probability measure on U. The decision-theoretic procedure in this section adopts two states and three actions. The row states is express an element is in X or not, respectively. The set of actions is by a interval-valued matrix shown in Table 5. The subscript X represents this loss function is for X, which is omitted in the following.

The expected losses of each action for object are as follows:

Table 5. The interval-valued loss function for X.

In Table 5, and are lower bound and upper bound of ., , and indicates the costs for taking actions of, , and,respectively, when an element is in X. Equally, , and denotes the losses for taking the same actions when an element belongs to. On the basis of conditions in Table 5, a particular kind of loss function is considered:

Likewise, is the description of x based on the IF relation, i.e. and it is assumed that.

Proposition 4.2.1 Note that and are two IF condition probabilities. X is a classical event,., and. If and, then

(12)

is called the conditional probability of X given, is called the conditional probability of X given.

In light of Bayesian decision procedure, the decision rules in Section 2 could be re-expressed as follows:

If and, deciding;

If and, deciding.

If the remainder elements x’s satisfying neither nor, we decide;

Definition 4.2.1 Let be an IF probabilistic approximation space. The loss function is the interval value. The are defined as follows:

In the IF relation, the [λ]-IF probability upper approximation and the [λ]-IF probability upper approximation are respectively:

is called the [λ]-IF probability rough set of X.

The decision rules are the three-way decisions, which have three regions:, and. These rules mainly rely on the comparisons among, and which are essentially computing the IF probabilities. Therefore, the conditions for calculating decision rules are as follows.

For the rule:

For the rule:

Therefore, in light of Bayesian decision procedure, the decision rules could be rewritten as follows:

If and , then decide;

If and , then decide.

If the remainder elements x’s satisfying neither nor, then decide;

Where

For any interval valued we define “” operations and “” relation as follows:

Proposition 4.2.2 For simplicity, it is denoted by, and. In this case, we have the following simplified IF probability region:

In the fuzzy relation R, the fuzzy probability upper approximation and the fuzzy probability of X are respectively:

is called the -IF probability rough set of X.

Under the discussions in Proposition 4.2.2, the additional conditions of decision rule suggest that, namely, it follows that, the rules are:

If, then decide;

If, then decide;

If the remainder elements x’s satisfying neither nor, then decide;

Proposition 4.2.3 In this case, we have the following simplified IF probability region:

In the IF relation, the IF probability lower approximation and the IF probability upper approximation of X are respectively:

is called the -IF probability rough set of X.

According to decision-theoretic rough set, suppose the loss function satisfies, and , then we can get . Meanwhile, this paper also discusses the relationship between the value of and 1.

Case 1: When, the loss function must satisfies ;

Case 2: When, the loss function must satisfies ;

Case 3: When, the loss function must satisfies .

4.3. Case Study

Now continue to use case 3.3 as the research object, and make the rough set theory of decision making under the IF probability approximation space. On the basis of Table 2, the hypothesis is a IF probability approximation space, including, is a IF relation, as shown in Table 6. Now assume that the preference probability distribution on U is, , , , , , , , ,. Let denotes a decision class in which the classes are excellent. In the Bayesian decision process, some experts will provide values of the loss function for X, i.e.. It exhibits three cases in Table 7. Consider the loss function of Table 7, there are;; .

And the IF conditional probabilities for every are computed as follows (by Equations. (12)):

Table 6. A IF relation on U.

Table 7. Three cases of loss function.

, ,

, ,

, ,

, ,

,.

Case 1: When, namely, , it follows that

,.

and

, ,

.

Based on these achievements, we can get the corresponding decision rules as follows:

The investors most probably choose this scheme.

The investors are less likely to invest.

We are not sure for who need further investigation.

Case 2: When, namely, , it follows that

,.

and

, ,

.

According to the calculation results, the decision rules in case 2 can present as follows:

The investors most probably choose this scheme;

The are less likely to invest.

We are not sure for who need further investigation.

Case 3: When, namely, , it follows that

,.

and

, ,

.

Analogously, we can get the rest of the decision rules associate with these rough regions, as follows:

The investors most probably choose this scheme;

The are less likely to invest;

We are not sure for who need further investigation.

5. Conclusions

The DTRS proposed by Yao et al. is an important development of Pawlak’s rough set theory. We introduced different relations to convert IFIS into fuzzy and IF approximation spaces, respectively. By considering fuzzy probability and IF probability, FDTRS model and IFDTRS model have been established in our work. The main contributions of this paper are as follows. Firstly, FDTRS is discussed in the frame of fuzzy probability approximation spaces, and the corresponding measures and performance are discussed. Secondly, in order to deal with actual situation, we also study IFDTRS model in the frame of IF probability approximation spaces. Finally, we have constructed a case study about risk investment to explain and illustrate decision-making model. In the future, we will investigates other new decision-making methods and the corresponding states being IF sets.

Acknowledgements

This work is supported by the Natural Science Foundation of China (Nos. 61976245, 61772002), the Science and Technology Research Program of Chongqing Municipal Education Commission (No.KJ1709221), and the Fundamental Research Funds for the Central Universities (No. XDJK2019B029).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Pawlak, Z., Grzymala-Busse, J., Slowinski, R., et al. (1982) Rough Sets. International Journal of Parallel Programming, 11, 341-356.
[2]	Wang, G.Y., Yao, Y.Y. and Yu, H. (2009) A Survey on Rough Set Theory and Applications. Chinese Journal of Computers, 32, 1229-1246. https://doi.org/10.3724/SP.J.1016.2009.01229
[3]	Xu, W. and Guo, Y. (2016) Generalized Multigranulation Double-Quantitative Decision-Theoretic Rough Set. Knowledge-Based Systems, 105, 190-205. https://doi.org/10.1016/j.knosys.2016.05.021
[4]	Zhang, W. (2006) Research on Rough Upper and Lower Approximation of Fuzzy Attribution Set. Computer Engineering Applications, 42, 66-69.
[5]	Feng, L., Xu, S., Wang, F., Liu, S. and Qiao, H. (2019) Rough Extreme Learning Machine: A New Classification Method Based on Uncertainty Measure. Neurocomputing, 325, 269-282. https://doi.org/10.1016/j.neucom.2018.09.062
[6]	Mahajan, P., Kandwal, R. and Vijay, R. (2012) Rough Set Approach in Machine Learning: A Review. International Journal of Computer Applications, 56, 1-13. https://doi.org/10.5120/8924-2996
[7]	Hassan, Y.F. (2018) Rough Set Machine Translation Using Deep Structure and Transfer Learning. Journal of Intelligent & Fuzzy Systems, 34, 4149-4159. https://doi.org/10.3233/JIFS-171742
[8]	Moshkov, M. and Zielosko, B. (2013) Combinatorial Machine Learning: A Rough Set Approach. Springer Publishing Company, Incorporated, New York.
[9]	Vluymans, S., Deer, L., Saeys, Y. and Chris, C. (2015) Applications of Fuzzy Rough Set Theory in Machine Learning: a Survey. Games Economic Behavior, 142, 53-86. https://doi.org/10.3233/FI-2015-1284
[10]	Wei, W. and Li, H. (2010) Machine Learning Applications in Rough Set Theory. 2010 International Conference on Internet Technology and Applications, Wuhan, 20-22 August 2010, 1-3. https://doi.org/10.1109/ITAPP.2010.5566567
[11]	Tiwari, A., Tiwari, A.K., Saini, H.C., et al. (2013) A Cloud Computing Using Rough Set Theory for Cloud Service Parameters through Ontology in Cloud Simulator. 2013 International Conference on Advances in Computing Information Technology, 1-9. https://doi.org/10.5121/csit.2013.3401
[12]	Deng, S., Zhou, A.H., Yue, D., et al. (2017) Distributed Intrusion Detection Based on Hybrid Gene Expression Programming and Cloud Computing in a Cyber Physical Power System. IET Control Theory and Applications, 11, 1822-1829. https://doi.org/10.1049/iet-cta.2016.1401
[13]	Kobayashi, M. and Niwa, K. (2018) Method for Grouping of Customers and Aesthetic Design Based on Rough Set Theory. Computer-Aided Design and Applications, 15, 1-10. https://doi.org/10.1080/16864360.2017.1419644
[14]	Tiwari, A., Sah, M.K. and Gupta, S. (2015) Efficient Service Utilization in Cloud Computing Exploitation Victimization as Revised Rough Set Optimization Service Parameters. Procedia Computer Science, 70, 610-617. https://doi.org/10.1016/j.procs.2015.10.050
[15]	Peters, J.F. and Skowron, A. (2002) A Rough Set Approach to Knowledge Discovery. International Journal of Intelligent Systems, 17, 109-112. https://doi.org/10.1002/int.10010
[16]	Cao, L.X., Huang, G.Q. and Chai, W.W. (2017) A Knowledge Discovery Model for Third-Party Payment Networks Based on Rough Set Theory. Journal of Intelligent & Fuzzy Systems, 33, 413-421. https://doi.org/10.3233/JIFS-161738
[17]	Ohrn, A. and Rowland, T. (2000) Rough Sets: A Knowledge Discovery Technique for Multifactorial Medical Outcomes. American Journal of Physical Medicine Rehabilitation, 79, 100. https://doi.org/10.1097/00002060-200001000-00022
[18]	Hu, X. (1996) Knowledge Discovery in Databases: An Attribute-Oriented Rough Set Approach. University of Regina, Regina.
[19]	Wen, W. (2010) The Construction of Decision Tree Information Processing System Based on Rough Set Theory. 2010 Third International Symposium on Information Processing, Qingdao, 15-17 October 2010, 546-549. https://doi.org/10.1109/ISIP.2010.147
[20]	Maji, P. and Mahapatra, S. (2019) Rough-Fuzzy Circular Clustering for Color Normalization of Histological Images. Fundamenta Informaticae, 164, 103-117. https://doi.org/10.3233/FI-2019-1756
[21]	Dntsch, I., Gediga, G. and Gediga, G. (1998) Uncertainty Measures of Rough Set Prediction. Artificial Intelligence, 106, 109-137. https://doi.org/10.1016/S0004-3702(98)00091-5
[22]	Zak, M. (2016) Non-Newtonian Aspects of Artificial Intelligence. Foundations of Physics, 46, 517-553. https://doi.org/10.1007/s10701-015-9977-3
[23]	Kitano, H. (2016) Artificial Intelligence to Win the Nobel Prize and Beyond: Creating the Engine for Scientific Discovery. Ai Magazine. https://doi.org/10.1609/aimag.v37i1.2642
[24]	Hajjar, Z., Khodadadi, A., Mortazavi, Y., et al. (2016) Artificial Intelligence Modeling of DME Conversion to Gasoline and Light Olefins over Modified Nano ZSM-5 Catalysts. Fuel, 179, 79-86. https://doi.org/10.1016/j.fuel.2016.03.046
[25]	Afan, H.A., El-Shafie, A., Wan, H.M.W.M., et al. (2016) Past, Present and Prospect of an Artificial Intelligence (AI) Based Model for Sediment Transport Prediction. Journal of Hydrology, 541, 902-913. https://doi.org/10.1016/j.jhydrol.2016.07.048
[26]	Srimathi, S. and Sairam, N. (2014) A Soft Computing System to Investigate Hepatitis Using Rough Set Reducts Classified by Feed Forward Neural Networks. International Journal of Applied Engineering Research, 9, 1265-1278.
[27]	Ding, W., Lin, C.T. and Prasad, M. (2018) Hierarchical Co-Evolutionary Clustering Tree-Based Rough Feature Game Equilibrium Selection and Its Application in Neonatal Cerebral Cortex MRI. Expert Systems with Applications, 101, 243-257. https://doi.org/10.1016/j.eswa.2018.01.053
[28]	Pal, S.S. and Kar, S. (2019) Time Series Forecasting for Stock Market Prediction through Data Discretization by Fuzzistics and Rule Generation by Rough Set Theory. Mathematics and Computers in Simulation, 162, 18-30. https://doi.org/10.1016/j.matcom.2019.01.001
[29]	Atanassov, K. and Rangasamy, P. (1986) Intuitionistic Fuzzy Sets. Fuzzy Sets Systems, 20, 87-96. https://doi.org/10.1016/S0165-0114(86)80034-3
[30]	Szmidt, E. and Kacprzyk, J. (2003) An Intuitionistic Fuzzy Set Based Approach to Intelligent Data Analysis: An Application to Medical Diagnosis. In: Abraham, A., Jain, L.C. and Kacprzyk, J., Eds., Recent Advances in Intelligent Paradigms and Applications, Physica-Verlag GmbH, Heidelberg, 57-70. https://doi.org/10.1007/978-3-7908-1770-6_3
[31]	Szmidt, E. and Kacprzyk, J. (2001) Intuitionistic Fuzzy Sets in Intelligent Data Analysis for Medical Diagnosis. Lecture Notes in Computer Science, 2074, 263-271. https://doi.org/10.1007/3-540-45718-6_30
[32]	Miguel, L., Vadim, L., Irina, L., Ragab, A. and Yacout, S. (2019) Recent Advances in the Theory and Practice of Logical Analysis of Data. European Journal of Operational Research, 275, 1-15. https://doi.org/10.1016/j.ejor.2018.06.011
[33]	Meng, F. and Chen, X. (2016) Entropy and Similarity Measure of Atanassov’s Intuitionistic Fuzzy Sets and Their Application to Pattern Recognition Based on Fuzzy Measures. Pattern Analysis and Applications, 19, 11-20. https://doi.org/10.1007/s10044-014-0378-6
[34]	Zhang, J.L., Williams, S.O. and Wang, H.X. (2018) Intelligent Computing System Based on Pattern Recognition and Data Mining Algorithms. Sustainable Computing-Informatics & Systems, 20, 192-202. https://doi.org/10.1016/j.suscom.2017.10.010
[35]	Acharjya, D. and Chowdhary, C.L. (2016) A Hybrid Scheme for Breast Cancer Detection Using Intuitionistic Fuzzy Rough Set Technique. International Journal of Healthcare Information Systems and Informatics, 11, 38-61. https://doi.org/10.4018/IJHISI.2016040103
[36]	Xu, W., Liu, Y. and Sun, W. (2012) Upper Approximation Reduction Based on Intuitionistic Fuzzy T, Equivalence Information Systems. . In: Li, T., et al., Eds., Rough Sets and Knowledge Technology. RSKT 2012. Lecture Notes in Computer Science, Springer-Verlag, Berlin, Heidelberg, 55-62. https://doi.org/10.1007/978-3-642-31900-6_8
[37]	Zhu, X.D., Wang, H.S. and Lu, J. (2012) Intuitionistic Fuzzy Set Based Fuzzy Information System Model. Kongzhi Yu Juece/Control Decision, 27, 1337-1342.
[38]	Zhang, X. and Chen, D. (2014) Generalized Dominance-Based Rough Set Model for the Dominance Intuitionistic Fuzzy Information Systems. In: Miao, D., Pedrycz, W., Ślȩzak, D., Peters, G., Hu, Q. and Wang, R., Eds., Rough Sets and Knowledge Technology. RSKT 2014. Lecture Notes in Computer Science, Springer, Cham, 3-14. https://doi.org/10.1007/978-3-319-11740-9_1
[39]	Yue, Z. and Jia, Y. (2015) A Group Decision Making Model with Hybrid Intuitionistic Fuzzy Information. Computers Industrial Engineering, 87, 202-212. https://doi.org/10.1016/j.cie.2015.05.016
[40]	Feng, T., Mi, J.S. and Zhang, S.P. (2012) Belief Functions on General Intuitionistic Fuzzy Information Systems. Information Sciences, 271, 143-158. https://doi.org/10.1016/j.ins.2014.02.120
[41]	Yu, S. and Xu, Z. (2016) Definite Integrals of Multiplicative Intuitionistic Fuzzy Information in Decision Making. Knowledge-Based Systems, 100, 59-73. https://doi.org/10.1016/j.knosys.2016.02.007
[42]	Yao, Y.Y., Wong, S.K.M. and Lingras, P. (1990) A Decision-Theoretic Rough Set Model. Proceedings of the 5th International Symposium on Methodologies for Intelligent System, 25-27 October 1990.
[43]	Yao, Y. and Zhao, Y. (2008) Attribute Reduction in Decision-Theoretic Rough Set Models. Information Sciences, 178, 3356-3373. https://doi.org/10.1016/j.ins.2008.05.010
[44]	Yao, Y. (2011) Two Semantic Issues in a Probabilistic Rough Set Model. Fundamenta Informaticae, 108, 249-265.
[45]	Yao, Y. (2011) The Superiority of Three-Way Decisions in Probabilistic Rough Set Models. Information Sciences, 181, 1080-1096. https://doi.org/10.1016/j.ins.2010.11.019
[46]	Yao, Y. and Zhou, B. (2010) Naive Bayesian Rough Sets. In: Yu, J., Greco, S., Lingras, P., Wang, G. and Skowron, A., Eds., Rough Set and Knowledge Technology. RSKT 2010. Lecture Notes in Computer Science, Springer, Berlin, Heidelberg, 719-726. https://doi.org/10.1007/978-3-642-16248-0_97
[47]	Yao, Y. (2007) Decision-Theoretic Rough Set Models. Lecture Notes in Computer Science, 178, 1-12. https://doi.org/10.1007/978-3-540-72458-2_1
[48]	Li, Y., Zhang, C. and Swan, J.R. (1999) Rough Set Based Decision Model in Information Retrieval and Filtering.
[49]	Li, Y., Zhang, C. and Swan, J. (2000) An Information Filtering Model on the Web and Its Application in Job Agent. Knowledge-Based Systems, 13, 285-296. https://doi.org/10.1016/S0950-7051(00)00088-5
[50]	Zhou, B., Yao, Y. and Luo, J. (2010) A Three-Way Decision Approach to Email Spam Filtering. In: Advances in Artificial Intelligence, Springer, Berlin, Heidelberg, 28-39. https://doi.org/10.1007/978-3-642-13059-5_6
[51]	Zhou, X. and Li, H. (2009) A Multi-View Decision Model Based on Decision-Theoretic Rough Set. In: Rough Sets and Knowledge Technology, Springer, Berlin, Heidelberg, 650-657. https://doi.org/10.1007/978-3-642-02962-2_82
[52]	Miao, Y. and Qiu, X. (2009) Hierarchical Centroid-Based Classier for Large Scale Text Classification.
[53]	Yao, J.T. and Herbert, J.P. (2007) Web-Based Support Systems with Rough Set Analysis. In: Rough Sets and Intelligent Systems Paradigms, Springer, Berlin, Heidelberg.
[54]	Li, H. and Zhou, X.Z. (2013) Risk Decision Making Based on Decision-Theoretic Rough Set: A Three-Way View Decision Model. International Journal of Computational Intelligence Systems, 4, 1-11. https://doi.org/10.1080/18756891.2011.9727759
[55]	Liu, D., Yao, Y.Y. and Li, T.R. (2011) Three-Way Investment Decisions with Decision-Theoretic Rough Sets. International Journal of Computational Intelligence Systems, 4, 66-74. https://doi.org/10.1080/18756891.2011.9727764
[56]	Yao, Y. and Deng, X. (2010) Sequential Three-Way Decisions with Probabilistic Rough Sets. Information Sciences, 180, 341-353. https://doi.org/10.1016/j.ins.2009.09.021
[57]	Yao, Y. (2008) Probabilistic Rough Set Approximations. International Journal of Approximate Reasoning, 49, 255-271. https://doi.org/10.1016/j.ijar.2007.05.019
[58]	Yao, Y.Y. (2003) Probabilistic Approaches to Rough Sets. Expert Systems, 20, 287-297. https://doi.org/10.1111/1468-0394.00253
[59]	Liu, D., Li, T. and Ruan, D. (2011) Probabilistic Model Criteria with Decision-Theoretic Rough Sets. Information Sciences, 181, 3709-3722. https://doi.org/10.1016/j.ins.2011.04.039
[60]	Yang, H.L., Liao, X., Wang, S. and Wang, J. (2013) Fuzzy Probabilistic Rough Set Model on Two Universes and Its Applications. International Journal of Approximate Reasoning, 54, 1410-1420. https://doi.org/10.1016/j.ijar.2013.05.001
[61]	Takahashi, H. (2017) On a Definition of Random Sequences with Respect to Conditional Probability. Information Computation, 206, 1375-1382. https://doi.org/10.1016/j.ic.2008.08.003
[62]	Akiyama, Y., Nolan, J., Darrah, M., Rahem, M.A. and Wang, L. (2016) A Method for Measuring Consensus within Groups: An Index of Disagreement via Conditional Probability. Information Sciences, 345, 116-128. https://doi.org/10.1016/j.ins.2016.01.052
[63]	Petturiti, D. and Vantaggi, B. (2016) Envelopes of Conditional Probabilities Extending a Strategy and a Prior Probability. International Journal of Approximate Reasoning, 81, 160-182. https://doi.org/10.1016/j.ijar.2016.11.014
[64]	Sun, B., Ma, W. and Zhao, H. (2014) Decision-Theoretic Rough Fuzzy Set Model and Application. Information Sciences, 283, 180-196. https://doi.org/10.1016/j.ins.2014.06.045
[65]	Zadeh, L.A. (1996) Fuzzy Sets. Fuzzy Sets, Fuzzy Logic, Fuzzy Systems. World Scientific Publishing Co. Inc., Singapore, 394-432. https://doi.org/10.1142/9789814261302_0021
[66]	Czogala, E., Drewniak, J. and Pedrycz, W. (1982) Fuzzy Relation Equations on a Finite Set. Fuzzy Sets Systems, 7, 89-101. https://doi.org/10.1016/0165-0114(82)90043-4
[67]	Zadeh, L.A. (1968) Probability Measures of Fuzzy Events. Journal of Mathematical Analysis Applications, 23, 421-427. https://doi.org/10.1016/0022-247X(68)90078-4