Numerical Simulation of the Natural Convection in a Tunnel Whose Floor Has a Variable Sinusoid with a Roof Opening ()
1. Introduction
Modeling heat transfer in cavities like tunnels, by natural convection, has been the subject of many researches ranging from geothermal modeling to bioengineering or electronics. The effect of geometry on the thermodynamic behavior of these cavities has aroused much interest among researchers [1] [2] [3]. In the logic of pushing the research on the effect of the form factor on the natural convection, we carry out the study in a tunnel whose horizontal ceiling brought to the temperature Tg presents an opening and we progressively vary the amplitude of the sinusoidal floor brought to temperature Tf. Since the appearance of the first tunnels a lot of investigation going from the ventilation to the smoke extraction came into being in order to make more practical and to maintain these structures [4]. Thus, the study of the behavior of different fluids in the latter has been the center of many experimental, theoretical or numerical investigations. Therefore, the wide application domains of natural convection heat transfer and the absence of analytical solutions to the equations that model this phenomenon require a good knowledge of numerical resolution processes [5]. In order to better understand the physical phenomena that come into play, many geometry models or fluid types have been used in previous research [6] [7] [8] [9] [10]. In the literature many studies on the natural convection of the air in tunnel have been performed. On the other hand, many of these works are focused only on the effect of the sinusoidal amplitude or its periodic effect on thermoconvective flow. The impacts of the control parameters such as the height and amplitude of the sinusoid are not studied simultaneously in these studies. Thus, to take into account the influence of the geometry variation on the simulation’s results,
different values of the form factors like the height of the tunnel  and the
and the
amplitude of the sinusoid δ presented (Table 1) have been studied. Taking into account the simultaneous variation of Λ and δ we end up with 9 cases of figures thus generalizing the preceding works.
2. Material and Numerical Method
To establish the natural convection we are studying, we have applied the formalism vorticity-stream function to the adimensional equations of Navier stocks and energy that govern the flow of fluid in our tunnel whose form factors are shown in the table below.
With vorticity  and
and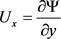 ;
; 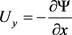
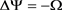


![]()
Table 1. Geometry presentation for different shapes.
Peclet number (dimensionless) 
Reynolds number (dimensionless) 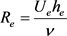
Our problem, which is described by the equations above, does not admit analytical solutions except in very simplified cases. Therefore obtaining exact analytical solution of the equations being almost impossible; To solve this problem we used the finite volume method and the governing equations with appropriate boundary conditions are solved under steady, incompressible conditions with the Boussinesq approximation using the comlputational fluide dynamic(CFD) [11] [12] [13] [14] [15]. The finite volume method is more efficient than the classical methods based on finite differences in the treatment of problems with complex geometry, particularly two-dimensional ones. It is more economical in terms of time and volume of calculation while guaranteeing a high stability with respect to calculations. The turbulent momentum and heat fluxes studied in this problem were modeled by a confined flow K-ω SST viscosity model which is a combination of the K-ω model near the walls and K-ε at the heart of the flow. The choice of the fineness of the mesh is a delicate problem and more particularly in our case because of the presence of sinusoid at the level of the floor and the roof opening. It is then necessary to make a mesh sufficiently fine so that the results have a good precision and reproduce all the phenomena without however leading to enormous computing times. Therefore, we used a fine mesh at the beginning of the sinusoid for all the geometries thus obtaining meshes with an Y + < 5 shown in Figure 1 To implement the dimensions corresponding to the form factors given in Table 1, we drew the 2D geometry with the Ansys Fluent 19.0 geometry modeler, shown in Figure 2.
3. Results and Discussions
In the logic of validating our work, we have approached the results obtained (isothrems and streamelines) with the results obtained by P. K. Das [1] far from the aperture and the sinusoid thus corresponding to the study between two plane plates. And we find that the results are almost identical for the Rayleigh number equal to 2 × 104 and Pr = 0.71. In the following, to better visualize the effects of form factors on the isothrems and streamelines we will display the results from the input of the sinusoid to the right wall.
![]() (a)
(a)![]() (b)
(b)
Figure 2. (a) Tunnel geometry; (b) Hybrid mesh.
3.1. The Flowfield
We performed the simulation for different Rayleigh numbers ranging from 2 × 104 to 7 × 106 (Figure 3), thus we find that the number of cells decreases considerably as we advance in the tunnel when the height Λ of the tunnel varies from 1/8 to 3/8. For the Rayleigh number equal to 2 × 104 and (Λ = 1/8) we find a symmetry of the two convolutional convective cells in the middle of the tunnel which is deformed with the increase of the amplitude of the sinusoid. This is due to the fact that as the amplitude of the sinusoid is increased, the heated fluid tends to cool rapidly before reaching the ceiling, thus causing the enlargement of one of the cells to the detriment the other. In addition to the low Rayleigh number cooling the heated fluid is favored by the opening in the middle of the ceiling with an increase in the amplitude of the current function due to a sharp increase in the velocity amplitude at the roof opening. This phenomenon becomes more and more important for the Rayleigh number Ra = 105 and (Λ = 1/4) with the total disappearance of the cell at the entrance of the sinusoid to form a single cell in the middle of the tunnel at δ = 3/2. For Rayleigh = 7 × 106 and (Λ = 3/8) already we find that from the first value of δ = 1/2 we have the presence of a single convective cell occupying the entire length of the sinusoid. This cell disappears progressively for δ = 1, giving rise to superimposed daughter cells perpendicular to the length of the tunnel. For Λ = 3/8 and δ = 3/2 a recirculation zone caused by a rise in temperature is formed in the middle of the tunnel and extends a little far from the outlet of the sinusoid. Thus, we can observe the appearance of areas of turbulence on the level of the sunisoid that increases by increasing the amplitude of the sinusoid.
3.2. Heat Transfer Distribution
Local Nusselt number distribution at the wavy bottom wall is shown in Figure 4, Nusselt number distribution profile is symmetric with respect to X = 0 for Λ = 1/8 and 1/4 with δ = 1/2. We also note that for δ = 1; 3/8 a deformation of the wave form of the Nusselt number in the middle of the tunnel becomes more and more important because of the disappearance of one of the convective cells. This
![]()
Figure 3. Presentation of isotherms (right) and streamlines (left) for different values of δ and Λ (Ra = 2 × 104; 105; 7 × 106).
periodic symmetry is due to the fact that the amplitude of the sinusoid is weak so we are closer to a plane plate with undisturbed convective cells. We find that for any value of δ the decrease of the number of convective cells as a function of the increase in Λ leads to a decrease in the number of ripples in the Nusselt number. And as the amplitude of the sinusoid increases, we notice a deformation of the periodic form in the middle of the tunnel caused by the appearance of turbulence zones in the middle of the sinusoid. Λ = 3/8 coresponding to Ra = 7 × 106
![]()
Figure 4. local Nusselt number of the wavy bottom obtained for different values of Λ and δ (Ra = 2 × 104; 105; 7 × 106).
the height of the tunnel is so sufisant that the exchange between the fluid and the floor is disturbed and from where the diformity on the wave profile of Nusselt number at the level of the sinusoid. So we can say that as the amplitude of the sinusoid is superior or equal to 1 for Λ = 3/8 instability develops inside the sinusoid creating the birth of many daughter cells.
4. Conclusion
Based on the numerical results carried out in this research programme, the numerical results we were allowed to pull a better understanding of the influence of shape factors on the thermodynamic transfer of the area in a confined space such as the case of the tunnel studied in this problem. The effects of the wavy surface, aspect ratio, and the variation in the number of Rayleigh on the local Nusselt number have examined using numerical simulations with Ansys Fluent [16]. We thus note that natural convection heat and fluid transfer is strongly influenced by the presence of sinusoid on the floor.
Acknowledgements
This work is the brainchild of the research group of Fluid Mechanics and Applications of Cheikh Anta Diop University of Dakar in collaboration with Dr. Ing. Bode Florin in Department of Mechanical Engineering at the Technical University of Cluj-Napoca, Romania.