Soliton-Like Spherical Symmetric Solutions of the Nonlinear Spinor Field Equations Depending on the Invariant Function IP=P2 in the General Relativity Theory ()
1. Introduction
The soliton as regular, localized energy density, finite total energy and stable solutions of nonlinear differential equations, is widely used in pure science. In the theory of General Relativity, this topic is dealt by many authors in various research works. The type soliton solutions are used to describe the structure of the elementary particles configuration. A. Adomou and G. N. Shikin [1] have obtained exact plane-symmetric solutions to the spinor field equations with nonlinear terms, which are arbitrary functions of
. They have clarified the role of nonlinear terms in the nonlinear field equations and the influence of the own gravitational field of elementary particles in the formation of regular localized soliton-like solutions. They have proved that the solutions obtained are particular to the metric because the total charge and the total spin are not limited. The spherical symmetric soliton-like solutions of the nonlinear spinor field equations in gravitational theory are got by V. Adanhoumè, A. Adomou, F. P. Codo and M. N. Hounkonnou [2]. They have studied in detail equations with power and polynomial nonlinearities. They have also proved that the soliton-like solutions exist in flat space-time. In the research work entitled ‘‘Plane-Symmetric Solitons of Spinor and Scalar Fields’’, B. Saha and G. N. Shikin [3] have obtained exact plane-symmetric solutions to the gravitational, spinor and scalar fields equations. On the one hand, the role of gravitational field in the formation of the field configuration with the total energy, the spin and the charge has been investigated. On the other hand, the influence of the change of the sign of energy density of the spinor and scalar fields on the properties of the configurations obtained has been examined. Their study has come out that the choice of spinor field nonlinearity can lead to the elimination of scalar field contribution to the metric functions, but leaving its contribution to the total energy unaltered. In a recent research work appeared in September 2019, which will be referred to part I of the present research work and entitled “Plane Symmetric Solutions to the Nonlinear Spinor Field Equations in General Relativity Theory”, A. Adomou, Jonas Edou and Siaka Massou [4] have obtained the general plane symmetric solutions to the spinor and gravitational fields equations. The nonlinear terms
in the lagrangian density are an arbitrary function
depending on the invariant function
. It is demonstrated that the static plane symmetric metric doesn’t convenient to obtain the soliton-like solutions with finite quantities of the total charge and the total spin. Therefore, they concluded that the consideration of the own gravitational field of the elementary particles and the nonlinearity of the spinor field in the lagrangian density are not sufficient in order to describe the configuration of elementary particles. The geometric properties of the metric must be taken into account. That is why, in this present study, considering the nonlinearity of the spinor field, the own gravitational field of elementary particles and changing the geometrical properties of the metric, we have extended the results initiated in [4] to exact spherical symmetric solutions.
The introduction represents Section 1 which generalizes the previous studies on the soliton model for the configuration of elementary particles in the gravitational theory. Note that the rest of this paper is organized as follows. Section 2 deals with basics nonlinear and gravitational fields equations and their general solutions. Then, taking into account the proper gravitational field of the elementary particles, we have solved nonlinear Dirac’s and Einstein’s equations. We have also analyzed the general solutions obtained for concrete nonlinear terms in the spinor lagrangian in Section 3. The paper is ended by the conclusion which represents Section 4 where we summarize our results and the perspectives of our research work in the future.
2. Basics Fields Equations and General Solutions
We choose the lagrangian of the self-consistent system of spinor and gravitational fields in the form [1] :
(1)
where R is the scalar curvature,
is Einstein’s gravitational constant, G is Newton’s gravitational constant,
is the nonlinear part of the spinor lagrangian and describes the self-interaction of the spinor field.
is an arbitrary function depending on the invariant
.
For a static spherically symmetric system an appropriate metric is considered under the form
(2)
here the velocity of light C is taken to be unity in geometric unity. In our study, the metric functions,
,
and
are functions depending on the single spatial variable
, where r stands for the radial component of the spherical symmetric metric, and obey the harmonic coordinate condition:
(3)
Let us now formulate the requirements to be fulfilled by soliton like-solutions. These are:
- stationarity (applied to metric (2)), i.e.,
- regularity of the metric and matter fields in the whole space-time;
- localisation in space-time (with finite energy).
The last requirement assumes the rapid decreasing of the energy density of the material field at spatial infinity, with together with the second one guarantees the finite value of
. The second requirement means the regularity of material fields as well as the regularity of metric functions, which entails the demand of finiteness of the energy-momentum tensor of material fields all over the space [3] [5].
The general form of Einstein equation is:
(4)
where
is the Einstein’s tensor;
is the Ricci’s tensor;
is the Kronecker’s symbol and
is the metric energy-momentum tensor of the spinor field.
Taking into account the metric tensor
, the larangian (1), the variational principle and usual algebraic manipulations, we obtain the nonzero components of the Einstein’s tensor
which represent the Einstein’s field equations for the metric (2) under the harmonic coordinate condition (3) [6] :
(5)
(6)
(7)
(8)
here prime (
) denotes differentiation with respect to
.
Variational method applied to (1) with respect to spinor fields
and
leads to nonlinear spinor field equations [7]
(9)
(10)
with
(11)
The corresponding metric energy-momentum tensor of the spinor field is
(12)
Otherwise
(13)
Using the spinor field Equations (9) and (10),
can be rewritten under the form
(14)
Taking into account the expression obtained previously in (14), let us write explicitly the nonzero components of the tensor
:
(15)
(16)
In (9)-(10) and (12)-(13),
denotes the covariant derivative of the spinor, having the form [7] [8] :
(17)
where
are the spinor affine connection matrices.
In curved space-time, the matrices
are defined in the following way.
From the equalities
(18)
where
,
are Dirac’s matrices in flat space-time,
are tetradic 4-vectors, we obtain
(19)
Using the expression
(20)
where
are Christoffel’s symbols, we get explicitly
(21)
According to the Einstein’s convention, we find
(22)
Taking into account the obtained expression for
(22), the Equations (9) and (10) may be rewritten as follows
(23)
(24)
Further setting
with
, for the components of spinor field, we get the following system of equations from (23)
(25)
(26)
(27)
(28)
The functions
,
,
and
are linked by the relation
(29)
Using the set of Equations (25)-(28), we define the functions
,
and
, by a first-order equations as follows
(30)
(31)
(32)
The previous equations system has for solution
(33)
C being an integration constant. The relation (33) proved that the gravitational field equations are naturelly nonlinear and the field itself is universal and unscreenable. It is also present in microcosm. The consideration of proper gravitational field is very important in order to define physical interesting properties of elementary particles. It is also signicantly influence the properties of interacting particles, mostly at high energies. We shall more prove the important of own gravitational field of elementary particle by investigating the properties of spinor and Einstein’s equations in flat space-time.
Taking into account the spinor field equation and the conjugate one respectively in their forms (23) and (24), we obtain another expression for
from (16):
(34)
Let us now solve the Einstein equations. In view of
, substraction of Einstein Equations (5) and (7) leads to the equation
(35)
The previous equation can be transformed into a Liouville equation [5] , to produce the solutions:
(36)
(37)
where K and B are integration constants.
The function T has the form
(38)
where h and
are integration constants.
Using the expressions (36) and (37), we find from the harmonic coordinate condition (3), the following expression of the metric function
.
(39)
We also define the relations between the metric functions
,
and
as follows
(40)
Equation (6) being the first integral of (5) and (7), is a first order differential equation. Putting the results (34) and (40) into (6), the Eintein equation
may be transformed under the form
(41)
Taking into account
and
, the general solutions to the Equation (41) are
(42)
Setting a concrete form of the function
, from (42) we can find
. If
is known, we can determine
from
. If 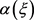 is known, we can determine
is known, we can determine  and
and 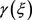 from (40).
from (40).
Note that, in the unified nonlinear spinor theory of Heisenberg, the massive term is absent, and according to Heisenberg, the particle mass should be obtained as a result of quantization of spinor prematter. It should be emphasized that in the nonlinear generalization of classical field equations, the massive term does not possess the same significance that it possesses in the linear one, as it by no means defines total energy (or mass) of the nonlinear field system [9].
Let us now resolve Equations (25)-(28) in more compact form in order to obtain a concrete form of the functions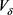 . In this perspective, when we take
. In this perspective, when we take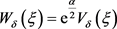 , we have the system of differential equations of the first order as follows:
, we have the system of differential equations of the first order as follows:
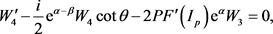 (43)
(43)
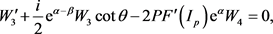 (44)
(44)
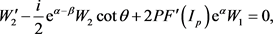 (45)
(45)
 (46)
(46)
where
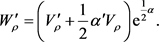 (47)
(47)
The precedent equations system leads to the following set of equations depending on functions of the argument , i.e.
, i.e.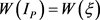 ,
, 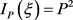 and
and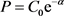 :
:
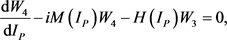 (48)
(48)
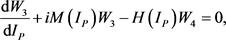 (49)
(49)
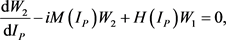 (50)
(50)
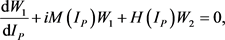 (51)
(51)
with ![]() and
and![]() .
.
Let us transform the set of first-order Equations (48)-(51) to the system of second-order differential equations. Differentiating Equation (48) in ![]() and substituting into the result Equation (49), we obtain a second-order equation for the function
and substituting into the result Equation (49), we obtain a second-order equation for the function ![]() as follows:
as follows:
![]() (52)
(52)
Differentiating also the Equation (49) in ![]() and substituting into the result Equation (48), we obtain the second-order equation for the function
and substituting into the result Equation (48), we obtain the second-order equation for the function ![]()
![]() (53)
(53)
By combining (52)-(53) and setting![]() , we obtain the following second-order differential equations obeyed by U:
, we obtain the following second-order differential equations obeyed by U:
![]() (54)
(54)
The Equation (54) is reduced to
![]() (55)
(55)
under the condition ![]() with
with![]() .
.
The Equation (55) has the first integral
![]() (56)
(56)
If![]() , then the Equation (56) has the solution
, then the Equation (56) has the solution
![]() (57)
(57)
If![]() , the solution of the equation of (56) is given by:
, the solution of the equation of (56) is given by:
![]() (58)
(58)
with
![]() (59)
(59)
By combining Equations (48) and (49) and taking into account (57) and (58), we get ![]() as follows:
as follows:
![]() (60)
(60)
![]() (61)
(61)
where ![]() and
and ![]() are integration constants.
are integration constants.
Solving analogously the Equations (50) and (51), we obtain the following expressions for ![]() and
and![]() :
:
![]() (62)
(62)
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
![]() (66)
(66)
where![]() ,
, ![]() and
and ![]() are integration constants.
are integration constants.
Using (57)-(61), we get the expressions of ![]() and
and ![]() as follows:
as follows:
![]() (67)
(67)
![]() (68)
(68)
![]() (69)
(69)
![]() (70)
(70)
where ![]() and
and![]() .
.
Analogously operating on the relations (62)-(66) leads to the functions ![]() and
and ![]() defined by the following expressions:
defined by the following expressions:
![]() (71)
(71)
![]() (72)
(72)
![]() (73)
(73)
![]() (74)
(74)
with ![]() and
and![]() .
.
From the expressions of ![]() defined previously, the analytics general solutions of the fundamental fields equations are
defined previously, the analytics general solutions of the fundamental fields equations are
![]() (75)
(75)
![]() (76)
(76)
![]() (77)
(77)
![]() (78)
(78)
where
![]() (79)
(79)
In the following paragraph, we will determine the solutions of the equations, taking the concrete analytics forms of the nonlinear terms.
3. Results and Discussions
In this section, we shall analyze the general results obtained in the previous section for concrete nonlinear terms of the arbitrary function ![]() in the lagrangian density.
in the lagrangian density.
We opt for the following polynomial form as follows:
![]() (80)
(80)
where ![]() is nonlinearity parameter and n power nonlinearity. It is convenient to separately analyze the two cases
is nonlinearity parameter and n power nonlinearity. It is convenient to separately analyze the two cases ![]() and
and![]() .
.
· For![]() ,
, ![]() we get the Ivanenko-Heisenberg type nonlinear spinor field equation:
we get the Ivanenko-Heisenberg type nonlinear spinor field equation:
![]() (81)
(81)
From (42) and setting![]() , without loss of generality, we obtain:
, without loss of generality, we obtain:
![]() (82)
(82)
The invariant function ![]() is defined as follows
is defined as follows
![]() (83)
(83)
From ![]() and the relation (40), we deduce the expressions of the metric functions
and the relation (40), we deduce the expressions of the metric functions![]() ,
, ![]() and
and![]() :
:
![]() (84)
(84)
![]() (85)
(85)
![]() (86)
(86)
Taking into account (83), the energy density is
![]() (87)
(87)
The energy density is bounded when![]() . Its minimum value is
. Its minimum value is ![]() and its maximum value is
and its maximum value is ![]() for
for![]() .
.
Using (87) the energy density per unit invariant volume is
![]() (88)
(88)
Let us note from (88) that the energy density per unit invariant volume of Heisenberg-Ivanenko type equation of a nonlinear spinor field is positive and is localized. Therefore, the total energy is finite. Finally, its value is given by the following expression:
![]() (89)
(89)
We conclude that the Equation (81) has soliton-like solutions. Here, the existence of the soliton-like configurations with localized energy density, finite total energy in Heisenberg-Ivanenko type nonlinear equation case is an interesting result.
· For![]() ,
, ![]() , according to (80) the Equation (42) has the solution
, according to (80) the Equation (42) has the solution
![]() (90)
(90)
From (15), the expression of the energy density ![]() is
is
![]() (91)
(91)
Let us remarck from (90) and (91) that the energy density ![]() has unlimited value when
has unlimited value when![]() ,
, ![]() , and the initial set of equations has no solution with localized energy density. Hence, the total energy has not a finite quantity. Since the energy density is not bounded, the soliton-like solutions are absent when the nonlinear terms are chosen under the form
, and the initial set of equations has no solution with localized energy density. Hence, the total energy has not a finite quantity. Since the energy density is not bounded, the soliton-like solutions are absent when the nonlinear terms are chosen under the form![]() .
.
When![]() , from (42), we have
, from (42), we have
![]() (92)
(92)
From (15), the energy density ![]() has the following expression
has the following expression
![]() (93)
(93)
We conclude from (93) that the energy density of a nonlinear spinor field is negative and is localized in space. As for the distribution of the spinor field energy density per unit invariant volume![]() , it’s given by
, it’s given by
![]() (94)
(94)
From which
![]() (95)
(95)
where
![]() (96)
(96)
The total energy is defined by
![]() (97)
(97)
The obtained solutions describe a nonlinear spinor field configuration with regular localized energy density ![]() and energy density per unit volume
and energy density per unit volume![]() , negative total energy E and the metric functions are regular and stationary. The solutions possess the properties of soliton-like solutions mentioned above in the section 2. They may be used in order to describe the properties of the field configuration of the elementary particles.
, negative total energy E and the metric functions are regular and stationary. The solutions possess the properties of soliton-like solutions mentioned above in the section 2. They may be used in order to describe the properties of the field configuration of the elementary particles.
Considering![]() , we can get an explicit form of the function
, we can get an explicit form of the function![]() . We have
. We have
![]() (98)
(98)
![]() (99)
(99)
![]() (100)
(100)
![]() (101)
(101)
where
![]() (102)
(102)
and
![]() (103)
(103)
We can then finally write the components of the function ![]() of the spinor field under the form:
of the spinor field under the form:
![]() (104)
(104)
From (104), we conclude that the function ![]() is regular.
is regular.
The solutions obtained describe the configuration of nonlinear spinor field with localized energy density. The energy density per unit invariant volume ![]() is also a localized function. The total energy has a finite and negative quantity. The metrics functions are stationnary and regular. Then, they are soliton-like solutions and must be used to describe the configuration of elementary particles.
is also a localized function. The total energy has a finite and negative quantity. The metrics functions are stationnary and regular. Then, they are soliton-like solutions and must be used to describe the configuration of elementary particles.
It is necessary to clarify the role of the nonlinear terms in the nonlinear field equations in the formation of regular localized soliton-like solutions. In this case, we must resolve Dirac’s equation and compare its solutions with solutions to nonlinear spinor equations.
The Dirac’s equation corresponds to the linear spinor equation where![]() . We obtain from (23)
. We obtain from (23)
![]() (105)
(105)
Then, according to (42), we get
![]() (106)
(106)
From![]() , we have
, we have
![]() (107)
(107)
Using (40), we define the functions ![]() and
and ![]() as follows
as follows
![]() (108)
(108)
![]() (109)
(109)
According to (15),
![]() (110)
(110)
The invarian function ![]() and the metric functions
and the metric functions![]() ,
, ![]() ,
, ![]() ,
, ![]() are regular. But the energy density is not localized. Here, it is clear that soliton-like solutions are not exist in the linear case. Moreover, From these results it is shown that to obtain the regular localized soliton-like solutions, the nonlinear terms are very important. In the following paragraph, we shall consider the case when the influence of the gravitational field is not taken account for proving the importance of the proper gravitational field of elementary particles in the configuration of their geometrical structures.
are regular. But the energy density is not localized. Here, it is clear that soliton-like solutions are not exist in the linear case. Moreover, From these results it is shown that to obtain the regular localized soliton-like solutions, the nonlinear terms are very important. In the following paragraph, we shall consider the case when the influence of the gravitational field is not taken account for proving the importance of the proper gravitational field of elementary particles in the configuration of their geometrical structures.
In order to determine the role of the own gravitational field in the formation of regular localized solutions of soliton-like type to nonlinear spinor field equations, it is necessary to consider solutions to the Equation (9) in flat space-time when ![]() in (2). It then follows that the set of equations for the functions
in (2). It then follows that the set of equations for the functions ![]() becomes
becomes
![]() (111)
(111)
![]() (112)
(112)
![]() (113)
(113)
![]() (114)
(114)
From![]() , we obtain the expressions of the functions
, we obtain the expressions of the functions![]() ,
, ![]() and
and ![]() as follows
as follows
![]() (115)
(115)
Introducing (115) into (15) we obtain the expression of the energy density![]() . Then, reporting the result obtained into (94) we get the energy density per unit invariant volume
. Then, reporting the result obtained into (94) we get the energy density per unit invariant volume![]() . They are defined by the following expressions:
. They are defined by the following expressions:
![]() (116)
(116)
As for the total energy, it is given by
![]() (117)
(117)
From (117), let us conclude that in the spherical symmetric metric the soliton-like configuration has finite positive energy in flat space-time case. Here, in our study the localization of the energy density and the finite value of the total energy are been improved by the geometrical properties of the metric in flat space-time. Indeed, in plane-symmetric metric, the energy density is not bounded and the total energy diverges [4].
The system of Equations (111)-(114) has the solutions
![]() (118)
(118)
![]() (119)
(119)
![]() (120)
(120)
![]() (121)
(121)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are four unknown integration constants. We have obtained the general solutions to the Equations (111)-(114), which are regular and contain four arbitrary constants. The examination of the results proves that the localized soliton type solutions exist well in the static spherical symmetric space-time without gravitation. So the proper gravitational field of elementary particles and the geometrical properties of the metric play an important role in the configuration of elementary particles. The gravitational field is nonlinear by nature and the field itself is universal and unscreenable. By ignoring the proper gravitational field leads to the elimination of the nonlinear terms in the lagrangian density of the spinor field. In clear, the nonlinearity of the spinor field vanishes when the proper gravitational of elementary particles is negliged. The following paragraph deals with the total charge and the total spin. Let us start with the components of spinor current.
are four unknown integration constants. We have obtained the general solutions to the Equations (111)-(114), which are regular and contain four arbitrary constants. The examination of the results proves that the localized soliton type solutions exist well in the static spherical symmetric space-time without gravitation. So the proper gravitational field of elementary particles and the geometrical properties of the metric play an important role in the configuration of elementary particles. The gravitational field is nonlinear by nature and the field itself is universal and unscreenable. By ignoring the proper gravitational field leads to the elimination of the nonlinear terms in the lagrangian density of the spinor field. In clear, the nonlinearity of the spinor field vanishes when the proper gravitational of elementary particles is negliged. The following paragraph deals with the total charge and the total spin. Let us start with the components of spinor current.
Using the solutions obtained (98)-(101), we can define the components of spinor current as in [8] :
![]() (122)
(122)
Taking into account that![]() , where
, where ![]() and
and ![]() , the general forms of the components of the current vector are given by the following expressions
, the general forms of the components of the current vector are given by the following expressions
![]() (123)
(123)
![]() (124)
(124)
![]() (125)
(125)
![]() (126)
(126)
The configuration is static. With this assumption, only one component ![]() is different to zero. The another components of the current vector
is different to zero. The another components of the current vector![]() ,
, ![]() and
and ![]() vanish. This leads to a choice between the constant of integration in the solutions to the spinor field equations and Einstein’s equations when
vanish. This leads to a choice between the constant of integration in the solutions to the spinor field equations and Einstein’s equations when![]() . In our analyze, we obtain
. In our analyze, we obtain![]() ,
, ![]() and
and ![]() and in addition
and in addition![]() . Thus, the component
. Thus, the component ![]() comes
comes
![]() (127)
(127)
The component ![]() defines the charge density
defines the charge density ![]() which is equal to chronometric invariant as follows
which is equal to chronometric invariant as follows
![]() (128)
(128)
The total charge of the spinor field is
![]() (129)
(129)
where ![]() represents the center of the field configuration and
represents the center of the field configuration and ![]() with
with ![]() defined by (96).
defined by (96).
The relation (129) proves that the total charge has a finite quanttity when the nonlinear therm in the spinor field lagrangian![]() ;
; ![]() and
and![]() . The analogous result can be found in [2]. The following paragraph will deal with to the spin tensor study.
. The analogous result can be found in [2]. The following paragraph will deal with to the spin tensor study.
As defines in [4] , the general form of the spin tensor for the spinor field is
![]() (130)
(130)
According to (130), the spatial density of the spin tensor ![]() is:
is:
![]() (131)
(131)
![]() (132)
(132)
![]() (133)
(133)
With (133), the chronometric invariant of the spatial density is
![]() (134)
(134)
Thus, the projection of the spin vector on the radial axis has the form:
![]() (135)
(135)
Note from (135) that the spin tensor of the spinor field has a finite value.
4. Conclusion
Taking into account the proper gravitational field of elementary particles, the solutions that we have obtained in this research work are soliton-like solutions. They are regular with a localized energy density and limited total energy. The metric functions are stationary, the total charge and the total spin have finite quantities else. The soliton-like solutions exist in flat space-time and absent in linear case. The nonlinear terms and the proper gravitational field play an important role in the obtaining of the soliton-like solutions. Note that in static plane symmetric metric, the charge Q and spin have no finite value but in the spherical static symmetric metric, those are finite. In the forthcoming paper, using the same metric, we shall investigate the solutions to the spinor field equations with the nonlinear terms which are arbitrary functions depending on the invariant function of bilinear forms ![]() in general relativity theory. The future work will generalize and will improve the previous studies.
in general relativity theory. The future work will generalize and will improve the previous studies.