Dispersive Traveling Wave Solution for Non-Linear Waves Dynamical Models

Kwasi Boateng^1*, Weigou Yang¹, Michael Ezra Otoo², David Yaro¹

¹Faculty of Science, Jiangsu University, Zhenjiang, China.
²Department of Mathematics, Presbyterian University College, Abetifi, Eastern Region, Ghana.

DOI: 10.4236/jamp.2019.710167                

Abstract

In waves dynamics, Generalized Kortewegde Vries (gKdV) equation and Sawada-Kotera equation (Ske) have been used to study nonlinear acoustic waves, an inharmonic lattice and Alfven waves in a collisionless plasma, and a lot of more important physical phenomena. In this paper, the simple equation method (SEM) is used to obtain new traveling wave solutions of gKdv and Ske. The physical properties of the obtained solutions are graphically illustrated using suitable parameters. The computational simplicity of the proposed method shows the robustness and efficiency of SEM.

Keywords

Simple Equation Method, Traveling Wave Solutions, Generalized Kortewegde Vries (gKdV), Sawada-Kotera Equation (Ske)

1. Introduction

The application of nonlinear partial differential equations is not limited to areas of mathematics exclusively but also applicable in other science aspects like physics and engineering. In the study of waves dynamics, Korteweg-deVries equation (gKdv) and Sawada-Kotera equation (Ske) are applied in nonlinear evolution equation of long waves of small or moderate amplitude in shallow water of uniform depth, nonlinear acoustic waves in an inharmonic lattice, Alfven waves in a collisionless plasma, and a lot of more important physical phenomena. In recent years, study of these two equations has been done to obtain the exact solution using different methods. Methods of obtaining analytical or exact solution to the gKdv and Ske nonlinear partial differential equations used by other researchers include the sine-cosine method [1], an auto-Blackland transformation [2], Hirota direct method [3], the projective Riccati equation method [4], the He’s variational method [5], the Hirota bilinear method [6], the symbolic computation method [7] [8], the Odd Hamiltonian structure [9], the extended tanh method [10], (G’/G)-expansion method [11], the sub-ODE method [12], the extended mapping method [13], the tanh-coth method [14], etc. The simple equation method for solving nonlinear partial differential equations has gained a lot of attention from researchers due to its simplicity and ability to extract novel traveling wave solutions. The approach has been successfully used by several authors for obtaining the exact solution of nonlinear partial differential equations but to the best of our knowledge it has not been used to solve the above mentioned equations, that is, gKdv and Ske. The principal aim of this article is to obtain exact traveling wave solutions which include periodic and soliton solution to a particular case of the gKdv and Ske by a variant of the Simple Equation Method (SEM). The paper is organized as follows, in Section 2, we describe the steps of the simple equation method, in Section 3, we obtain the exact solutions for the Generalized Korteweg-deVries equation and Sawada Kotera equations, Section 4 is the graphical representation of the solution, Section 5 is the conclusion.

2. Method Description

Simple Equation Method

This section presents the description and steps of the simple equation method. Considering a (1 + 1)-dimensional nonlinear partial differential equation given by

$G\left(\theta \mathrm{,}{\theta }_t\mathrm{,}{\theta }_x\mathrm{,}{\theta }_{tt}\mathrm{,}{\theta }_{tx}\mathrm{,}{\theta }_{xx}\right)=0$ (1)

$\theta$ is an unknown function which depends on the independent variables x and t, G is a polynomial of $\theta =\left(x,t\right)$ and its partial derivatives in which the highest order of the derivatives and the highest order of the nonlinear terms exist. The steps of the method are as follows:

First Step: The independent variables x and t are put together into one variable called the wave variable, $\lambda$. That is:

$\theta \left(x,t\right)=\theta \left(\lambda \right)=x\pm \nu t.$ (2)

Equation (2) is the traveling wave equation and $\nu$ is the speed of the traveling wave which is to be determined. The traveling wave equation allows us to transform the Equation (1) into an ordinary differential equation (ODE) that is:

$H\left(\theta \mathrm{,}-\nu {\theta }^{\prime }\mathrm{,}{\nu }^2{\theta }^{″}\mathrm{,}-\nu {\theta }^{″}\mathrm{,}{u}^{″}\mathrm{,}\cdots \right)=0$ (3)

where H is a polynomial and its derivatives with respect to $\lambda$.

Second Step: Expressing the solution of Equation (3) in the form of a finite series

$\theta ={\displaystyle \underset{j=0}{\overset{m}{\sum }}}{b}_j\left(P{\left(\lambda \right)}^j\right)$ (4)

where $P\left(\lambda \right)$ is a function that satisfies either the Bernoulli equation or the Riccati equation, $b_j$ ( $i=0,1,2,\cdots ,k$ ) are constant parameters to be determined. In this article we consider the Bernoulli and Riccati equations which are popular nonlinear ordinary differential equations and their solutions are given by elementary functions. The Bernoulli equation employed in this paper is expressed as

$P^{\prime }\left(\lambda \right)=aP\left(\lambda \right)+c{P}^2\left(\lambda \right)\mathrm{,}$ (5)

the Riccati equation is also expressed as

$P^{\prime }\left(\lambda \right)=\mu P^2\left(\lambda \right)+\sigma ,$ (6)

where, a, c and $\sigma$ are constant to be determined.

Third Step: Balancing the highest order of both the linear and nonlinear terms in Equation (3) gives the balance number m. Putting Equation (4) into Equation (3) with Equation (5) or Equation (6), makes the left hand side of Equation (2) to be transformed into a polynomial in $P\left(\lambda \right)$, all the coefficients of the polynomial is equated to zero to give set of algebraic expressions for $b_j,a,c\left(j=0,1,2,\cdots ,m\right)$. The constant parameters are obtained by solving the algebraic expressions.

Fouth Step: Suppose the constant $b_j,a,c\left(j=0,1,2,\cdots ,m\right)$ can be determined in step three, then the exact traveling wave solution for Equation (1) is obtained.

3. Application of the Method

3.1. Generalized Korteweg-deVries (gKdV) Equation

${\Theta }_t+\alpha \Theta {\Theta }_x+\beta {\Theta }_{xxx}=0.$ (7)

Generalized Kortewegde Vries (gKdV) equation is a one dimensional nonlinear partial differential equation introduced by D. Korteweg and G. de Vries in (1895) for mathematical explanation of solitary wave phenomenon discovered by S. Russell in 1855. This nonlinear partial differential equation describes long time evolution of dispersive waves and in particular, the propagation of long waves of small or moderate amplitude, traveling in nearly one direction without dissipation in water of uniform shallow. The gKdV equation admits a special form of the exact solution, the soliton which arises in many physical processes, such as water waves, internal gravity waves in stratified fluid, ion-acoustic waves in a plasma among others.

Taking a traveling wave to be

$\Theta \left(\lambda \right)=\Theta \left(x,t\right),\lambda =x+\nu t.$ (8)

Transforming Equation (7) into ODE using the traveling wave equation in Equation (8), this gives us

$\nu \Theta +\frac{\alpha }{2}{\Theta }^2+\beta {\Theta }^{″}=0.$ (9)

Balancing according to step three described above, the balancing number m is a positive integer which is obtained by balancing the highest order linear term (i.e., ${\Theta }^{″}$ ) with the highest order of the nonlinear term (i.e. ${\Theta }^2$ ) in Equation (9), which is $m+2=2m$, therefore $m=2$. Hence the solution of Equation (9) is given as:

$\Theta ={\displaystyle \underset{j=0}{\overset{2}{\sum }}}P{\left(\left(\lambda \right)\right)}^j=b_0+b_{1}P+b_2{P}^2,$ (10)

with P satisfying Equation (5) above in the case of Bernoulli, as a result, the following expressions are obtained

$\begin{array}{l}\Theta =b_0+b_{1}P+b_2{P}^2\\ {\Theta }^{\prime }=2c{P}^3{b}_2+c{P}^2{b}_1+2P^{2}a{b}_2+Pa{b}_1\\ {\Theta }^{″}=6c^2{P}^2{b}_2+2c^2{P}^3{b}_1+10c{P}^{3}a{b}_2+3c{P}^{2}a{b}_1+4P^2{a}^2{b}_2+P{a}^2{b}_1\\ {\Theta }^2=P^4{b}_2^2+2P^3{b}_1{b}_2+2P^2{b}_0{b}_2+P^2{b}_1^2+2P{b}_0{b}_1+b_0^2.\end{array}$ (11)

Putting Equation (10) and Equation (11) into Equation (9) and equating the coefficient of $P^j$ to zero, where $j\ge 0$ we have,

$\begin{array}{l}\nu b_1+\alpha b_0{b}_1+a^2\beta b_1=0\\ \nu b_2+\alpha \left(b_0{b}_2+\frac{b_1^2}{2}\right)+\beta \left(4a^2{b}_2+3ac{b}_1\right)=0\\ \alpha b_1{b}_2+\beta \left(10a{b}_{2}c+2c^2{b}_1\right)=0\\ \frac{\alpha }{2}{b}_2^2+6b_2{c}^2\beta =0\\ \nu b_0+\frac{\alpha }{2}{b}_0^2=0.\end{array}$ (12)

Computing Equation (12) for the parameters $b_0\mathrm{,}{b}_1\mathrm{,}{b}_2$ and $\nu$ the following two cases is obtained first case:

$b_0=0,b_1=-\frac{12a\beta c}{\alpha },b_2=-\frac{12\beta c^2}{\alpha },\nu =-a^2\beta ,ac\ne 0$,

second case:

$b_0=-\frac{2a^2\beta }{\alpha },b_1=-\frac{12a\beta c}{\alpha },b_2=-\frac{12\beta c^2}{\alpha },\nu =a^2\beta ,ac\ne 0$,

for $c<0,a>0$ the solution of Equation (7) for the first case of parameters is given by

$\begin{array}{c}{\Theta }_1\left(x,t\right)=-\frac{2a^2\beta }{\alpha }-\frac{12a\beta c}{\alpha }\left[\frac{a\times \exp \left[a\left(x-a^2\beta t\right)\right]}{1-c\exp \left[a\left(x-a^2\beta t\right)\right]}\right]\\ -\frac{12\beta c^2}{\alpha }{\left[\frac{a\times \exp \left[a\left(x-a^2\beta t\right)\right]}{1-c\exp \left[a\left(x-a^2\beta t\right)\right]}\right]}^2,\end{array}$ (13)

${\Theta }_1\left(x,t\right)=-\frac{2a^2\beta }{\alpha }-\frac{12a^2\beta c/\alpha \exp \left[a\left(x-a^2\beta t\right)\right]}{{\left(1-c\times \exp \left[a\left(x-a^2\beta t\right)\right]\right)}^2}.$ (14)

Again, for the solution of Equation (7) using the second case is given by

$\begin{array}{c}{\Theta }_2\left(x,t\right)=-\frac{2a^2\beta }{\alpha }-\frac{12a\beta c}{\alpha }\left[\frac{a\times \exp \left[a\left(x+a^2\beta t\right)\right]}{1-c\times \exp \left[a\left(x+a^2\beta t\right)\right]}\right]\\ -\frac{12\beta c^2}{\alpha }{\left[\frac{a\times \exp \left[a\left(x+a^2\beta t\right)\right]}{1-c\times \exp \left[a\left(x+a^2\beta t\right)\right]}\right]}^2,\end{array}$ (15)

${\Theta }_2\left(x\mathrm{,}t\right)=-\frac{2a^2\beta }{\alpha }-\frac{12a^2\beta c/\alpha \times \exp \left[a\left(x+a^2\beta t\right)\right]}{{\left(1-c\times \exp \left[a\left(x+a^2\beta t\right)\right]\right)}^2}\mathrm{.}$ (16)

On the other hand where the solution for Equation (7) using the first case is given by

(17)

(18)

also when the solution for Equation (7) using the second case is given by:

(19)

(20)

For

(21)

and P satisfying Equation (6) above in the case of Riccati, the following expressions are obtained,

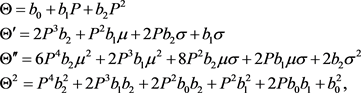(22)

Putting Equation (22) into Equation (9) and equating the coefficient of 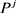to zero, where we have,

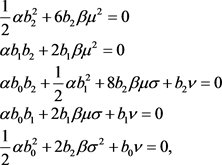(23)

computing Equation (23) for the parameters 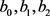and the following two cases are obtained,

first case:,

second case:.

For 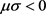the solution of Equation (7) for the first case of parameters is given by:

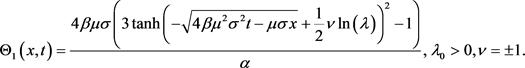(24)

again for the solution of Equation (7) using the second case is given by

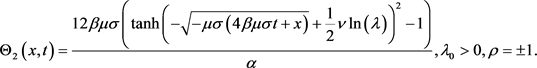(25)

for the solution of Equation (7) for the first case of parameters is given by

(26)

also for the solution of Equation (7) using the second case is given by

(27)

3.2. Application of the Simple Equation Method to the Sawada-Kotera Equation

This section uses the proposed method to obtain the exact solution of the (1+1)-dimensional Sawada-Kotera equation, is expressed as

(28)

the solutions of Equation (28) have been solved by different methods, but has not been solved anywhere with the simple equation method. Now using the proposed method in Section 2, we obtain the exact solution of Equation (28). Applying the transform wave equation of the form

(29)

to reduce Equation (28) into ordinary differential equation (ODE), given as

(30)

integrating Equation (30) with respect to we have,

(31)

Balancing the highest order of the linear term and that of the nonlinear term, it gives. For, the solutions of Equation (31) is expressed as

(32)

where are constants parameters, and

with P satisfying Equation (5) above in the case of Bernoulli equation the following expressions are obtained

(33)

Putting Equation (33) into Equation (31) and equating the coefficients of to be equal to zero, with, we have

(34)

the solution of Equation (34) exist only in the two cases below after solving:

First Case:

Second Case:

and

for the solution of Equation (28) for the first case of parameters is given by

(35)

again for the solution of Equation (28) using the second case is given by

(36)

and

(37)

On the other hand when the solution for Equation (28) using the first case is given by

(38)

Again for the solution of Equation (28) using the second case is given by

(39)

and

(40)

Again, P satisfying Equation (6) above in the case of Riccati, as a result, the following expressions are obtained

(41)

putting Equation (41) into Equation (31) and equating the coefficients of to be equal to zero, with, we have

(42)

the solution of Equation (42) exist only in the two cases below after solving:First Case:

Second Case:

and

For

the solution of Equation (28) for the first case of parameters is given by:

(43)

again for the solution of Equation (28) using the second case is given by

(44)

and

(45)

Figure 1. Plot of the exact traveling wave solutions of Equation (14) with parameters.

Figure 2. Plot of the exact traveling wave solutions of Equation (18) with parameters.

For the solution of Equation (28) for the first case of parameters is given by

(46)

again for the solution of Equation (28) using the second case is given by

(47)

and

(48)

Figure 3. Plot of the exact traveling wave solutions of Equation (27) with parameters.

Figure 4. Plot of the exact traveling wave solutions of Equation (35) with parameters and.

Figure 5. Plot of the exact traveling wave solutions of Equation (38) with parameters,.

Figure 6. Plot of the exact traveling wave solutions of Equation (48) with parameters.

4. Results and Discussion

This section compares existing literature results and the results obtained. With regards to the Generalized Kortewegde Vries equation, the solutions obtained in Equation (14), Equation (16), Equation (18) are almost similar to Ref.13. Again, for the solutions of the Sawada Kotera equation, solutions obtained in Equation (44), Equation (45) and Equation (46) are nearly similar to the solutions obtained by Ref.2. The rest of the solutions obtained in this paper are unique solutions which have not been stated before in existing literature. These solutions are applicable in long waves of small or moderate amplitude in shallow water of uniform depth, nonlinear acoustic waves in an inharmonic lattice, Alfven waves in a collisionless plasma, and a lot more important physical phenomena. Using suitable parameter values we illustrate the physical properties of some obtained results as shown in Figures 1-6.

5. Conclusion

In this research paper, the simple equation method has been used to obtain the exact solution of Generalized Korteweg de Vries (gKdV) and the Sawada Kotera nonlinear partial differential equation. These methods are used as the trial condition, since the simple equation method satisfies the first order Bernoulli differential equation or the first order Riccati differential equation. Using simple equation method, we derived a balance equation, by means of the balanced equations, exact solutions are obtained for the two equations. The exact solution attained from the proposed method implies that the approach is simple to apply and computationally feasible. The two NLPDEs under the study satisfy both the Bernoulli and Riccati differential equations. We then verified that the solutions obtained are the true solution to the original equation.

Acknowledgements

We thank the Editor and the referee for their comments. Research of K. Boateng is funded by the National Natural Science Foundation of China grant DMS 11571142. This support is greatly appreciated.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Bibi, S. and Mohyud-Din, S.T. (2014) Traveling Wave Solutions of KdVs Using Sine-Cosine Method. Journal of the Association of Arab Universities for Basic and Applied Sciences, 15, 90-93. https://doi.org/10.1016/j.jaubas.2013.03.006
[2]	Chen, B. and Xie, Y. (2005) An Auto-Backlund Transformation and Exact Solutions of Stochastic Wick-Type Sawada-Kotera Equations. Chaos, Solitons and Fractals, 23, 243-248. https://doi.org/10.1016/j.chaos.2004.04.021
[3]	Wazwaz, A. (2008) The Hirota’s Direct Method and the Tanh-Coth Method for Multiple Soliton Solutions of the Sawada-Kotera-Ito Seventh-Order Equation. Applied Mathematics and Computation, 199, 133-138. https://doi.org/10.1016/j.amc.2007.09.034
[4]	Salas, A. (2008) Some Solutions for a Type of Generalized Sawada-Kotera Equation. Applied Mathematics and Computation, 196, 812-817. https://doi.org/10.1016/j.amc.2007.07.013
[5]	Jafari, H., Yazdani, A., Vahidi, J. and Ganji, D.D. (2008) Application of He’s Variational Iteration Method for Solving Seventh Order Sawada-Kotera Equations. Applied Mathematical Sciences, 10, 471-477.
[6]	Liu, C. and Dai, Z. (2008) Exact Soliton Solutions for the Fifth-Order Sawada-Kotera Equation. Applied Mathematics and Computation, 206, 272-275. https://doi.org/10.1016/j.amc.2008.08.028
[7]	Zhang, J., Zhang, J. and Bo, L. (2008) Abundant Travelling Wave Solutions for KdV-Sawada Kotera Equation with Symbolic Computation. Applied Mathematics and Computation, 203, 233-237. https://doi.org/10.1016/j.amc.2008.04.035
[8]	Zhang, J., Wei, X. and Hou, J. (2010) Symbolic Computation of Exact Solutions for the Compound KdV-Sawada-Kotera Equation. International Journal of Computer Mathematics, 87, 94-102. https://doi.org/10.1080/00207160801965289
[9]	Popowicz, Z. (2009) Odd Hamiltonian Structure for Supersymmetric Sawada-Kotera Equation. Physics Letters A, 373, 3315-3323. https://doi.org/10.1016/j.physleta.2009.07.057
[10]	Wazwaz, A.M. (2007) The Extended Tanh Method for New Solitons Solutions for Many Forms of the Fifth-Order KdV Equations. Applied Mathematics and Computation, 184, 1002-1014. https://doi.org/10.1016/j.amc.2006.07.002
[11]	Li, Z.-L. (2010) Constructing of New Exact Solutions to the GKdV-mKdV Equation with Any-Order Nonlinear Terms by (G’/G)-Expansion Method. Applied Mathematics and Computation, 217, 1398-1403.
[12]	Li, X. and Wang, M. (2007) A Sub-ODE Method for Finding Exact Solutions of a Generalized KdV-mKdV Equation with High-Order Nonlinear Terms. Physics Letters A, 361, 115-118. https://doi.org/10.1016/j.physleta.2006.09.022
[13]	Wu, R. and Sun, J. (2007) Soliton-Like Solutions to the GKdV Equation by Extended Mapping Method. Chaos, Solitons & Fractals, 31, 70-74.
[14]	Gmez, C.A. and Salas, A.H. (2010) The Variational Iteration Method Combined with Improved Generalized Tanh-Coth Method Applied to Sawada-Kotera Equation. Applied Mathematics and Computation, 217, 1408-1414. https://doi.org/10.1016/j.amc.2009.05.046