1. Introduction and Theory
Rotating diffraction gratings have a number of applications. For example, a pair of counter rotating diffraction gratings can be used in laser beam scanners for obtaining a linear scan rate for a flat field recorder [1] . The Doppler frequency shift in various diffraction orders produced as a result of a rotating radial diffraction grating can be used for optical modulation [2] . Rotating all-glass diffraction gratings can be used as beam splitting frequency shifter in laser Doppler anemometers [3] . In this article, we study the general behavior of various diffracted lines as a result of rotation of the diffraction grating.
When a diffraction grating of line distance d is exposed to a light ray of wavelength
, the general equation for the condition of constructive interference is given by [4]
(1)
where n is any integer,
is the angle of nth-order diffraction, and
is the angle of incidence. Both
and
are considered positive if measured counterclockwise from the axis (normal to the diffraction grating) and negative if measured clockwise, as shown in Figure 1.
Now suppose that we illuminate a diffraction grating by a monochromatic ray of light of wavelength
and then turn the grating, keeping the direction of the incident light fixed, starting from normal incidence, the angle through which the grating turns would become the angle of incidence for light, which is
in Equation (1). However, instead of the diffraction angle
, let us study the angle of deviation
between a diffracted beam and the incident beam, as shown in Figure 2. As in the case of
and
, the angle
is positive if measured counterclockwise from the direction of incident light and negative if measured clockwise. Obviously, in terms of the deviation angle
, Equation (1) can be written as
(2)
where
is negative if the grating turns counterclockwise (Figure 2(a)) and positive if the grating turns clockwise (Figure 2(b)).
![]()
Figure 1. Slant incidence of a monochromatic light on a diffraction grating. For the situation shown
and
are both positive.
![]()
Figure 2. A diagram showing the angle of deviation
between a diffracted ray of light and the incident ray. The diffraction grating is rotated (a) counterclockwise (
) and (b) clockwise (
) relative to normal incidence.
The case
is trivial and leads to
. We are, however, interested in the higher-order diffractions and the behavior of
as a function of
. We shall only consider counterclockwise rotations of the diffraction grating (
) since clockwise rotations can be obtained from the former by a symmetry operation on the experimental setup. From Equation (2) we have
(3)
Let us investigate the behavior of this function, in particular, find out if there are any maxima or minima in
,
(4)
This expression becomes zero when
(5)
which reduces to
(6)
and becomes infinity if
(7)
which reduces to
(8)
In the last equation, the positive root will not be considered since it gives
(up to
for the choice of
and
), corresponding to a clockwise rotation. Therefore, the possibility of a minimum or maximum in Equation (3) exist only if one of the following conditions is satisfied:
(9)
We now consider each case separately.
Case 1:
For the counterclockwise rotations (
) that we are considering, we must have
. Furthermore, substituting the above equation into Equation (2), we obtain
(10)
Then adding the first of Equations (9) and (10) gives
(11)
or
(12)
which holds only if
. It is easily verified that under this condition,
, and hence
is a minimum.
Case 2:
Clearly this can hold only if
which corresponds to the diffracted rays below the normal to the grating (Figure 1). Substituting this result in Equation (1), we find
or
, which means that the diffracted ray is in the plane of the grating.
Therefore, our theoretical analysis shows that when the diffraction grating turns counterclockwise the diffracted rays with
go through a minimum angle of deviation. The minimum angle of deviation for the nth-order diffracted beam takes place when the grating rotates through an angle
relative to the normal incidence, given by
(13)
The minimum angle of deviation for the nth-order diffraction is then given by
(14)
There are no other minima or maxima in the angle of deviation.
2. Experiment and Results
In order to test these results, we used a diffraction grating with a line distance of
, and a 0.95 mW He-Ne laser (
). The line distance of the grating was obtained by measuring it at ten different points of the grating, using the laser light.
Table 1 shows the results of our measurements and their comparison with the calculated values. Each measured value reported in the table is the average of ten runs along with its standard deviation. The standard deviations of the theoretical values are calculated using propagation of errors and the standard deviation in d. As can be seen from Table 1, the agreement between the measured values and the calculated values is excellent.
Another interesting feature of these diffraction patterns is that the angle through which the grating has to turn for a diffraction line to go to its minimum deviation increases with the order of diffraction n. As a result, the angle between any two adjacent diffracted rays decreases first and then increases as the grating turns, resulting in a minimum value. To see this, we write Equation (3) for n and again for
, and subtract them to get
![]()
Table 1. Calculated and measured values of the rotation angle of the grating (
) at which the angle of deviation becomes a minimum,
. All angles are in degree.
(15)
Then differentiation of this equation with respect to
gives
(16)
which vanishes if and only if
(17)
It can easily be verified that when this condition is met,
is a minimum. Therefore, when
satisfies Equation (17), the angle between diffraction lines of order n and
becomes a minimum with a value given by
(18)
which is independent of n. Therefore the minimum angle reached between any two adjacent diffraction lines is the same.
Table 2 shows the values of
and
calculated from Equations (17) and (18), respectively. In this case it was difficult to find the value of
for which
goes to a minimum by watching the diffracted beams, as both
and
changed with
. We, therefore. measured
and
each as a function of
and then plotted
as a function of
. The minimum of each graph did in fact take place at a value of
very close to that predicted by Equation (17). The measured values of
are given in the last column of Table 2.
It should be pointed out that some of the results discussed in this work were experimentally observed by Lock [5] . However, as explained in the next section, he only provided a limited semi-quantitative analysis for his observations. Furthermore, the common practice in the diffraction grating measurements where the angle of diffraction is measured on both sides of the central maximum and then the average is calculated, is not falsified by the above asymmetric behavior
![]()
Table 2. Calculated and measured values of the minimum angle between adjacent diffraction line, and the rotation angles of the grating at which they occur. All angles are in degree.
of the diffraction angles. In fact, it turns out that the angle between the diffraction maxima with
and
is not sensitive to small deviations of the grating from being normal to the incident beam. To see this we consider the angle between the diffraction maxima with n and
:
(19)
Taking the derivative of this angle with respect to
, we find
(20)
which vanishes if and only if
. Therefore, the angle
having a stationary value at
, is not affected appreciably by small deviations of
from zero.
Finally, as an application of the above results, we rewrite Equation (14) as
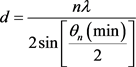 (21)
(21)
Since 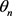 as a function of
as a function of  has a very flat minimum,
has a very flat minimum,  can be measured very accurately for a grating and hence the line distance d can be obtained from Equations (21) with high accuracy. Furthermore, in a single experiment data can be collected on several diffraction orders, resulting in a statistically even more accurate measurement of d. In these measurements the task of making the diffraction grating perpendicular to the incident light, which is normally required in the usual diffraction experiments, is eliminated.
can be measured very accurately for a grating and hence the line distance d can be obtained from Equations (21) with high accuracy. Furthermore, in a single experiment data can be collected on several diffraction orders, resulting in a statistically even more accurate measurement of d. In these measurements the task of making the diffraction grating perpendicular to the incident light, which is normally required in the usual diffraction experiments, is eliminated.
3. Summary
We investigated the diffraction patters of a rotated grating, from both theoretical and experimental points of view. The results of this investigation show several interesting behaviors of the system. First, as the grating rotates, the angle of deviation of each diffracted line relative to the incident light goes through a minimum. Although this behavior has been reported by Lock [5] , he only provided a semi-quantitative analysis of the problem based on two competing effects. Furthermore, Lock only considered the first- and second-order diffraction lines. In this work, we have provided a complete quantitative analysis of the problem and have considered up to the fifth-order diffraction.
Second, we have shown that the rotation angle of the grating that results in a minimum angle of deviation for a given diffracted line increases with the order of diffraction. As a result, the angle between any two successive diffracted lines first decreases and then increases, resulting in a minimum value which is the same for any two adjacent diffracted lines. This result has not been reported previously.
Third, it is shown that the angle between diffraction lines with 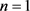 and
and 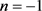 is not sensitive to small variations of the grating from being normal to the incident light, which justifies the commonly practiced procedure in diffraction experiments, again, an observation that is missing from previous investigations.
is not sensitive to small variations of the grating from being normal to the incident light, which justifies the commonly practiced procedure in diffraction experiments, again, an observation that is missing from previous investigations.
Finally, we have suggested a new method for determining the line distance of a diffraction grating with high accuracy.
Acknowledgements
This work was supported in part by a URAP grant from the University of Wisconsin-Parkside.