1. Introduction
Let
be the open unit disk in the complex plane
and let
be the Lebesgue area measure on
. For
the weighted Lebesgue measure
is defined by
where
is a normalizing constant so that
If
is a positive measure on
and
, we denote
the Lebesgue space over
with respect to
. That is,
consists of all functions f defined on
for which
For
and
, the weighted Bergman space
is defined by
, where
is the space of all analytic functions on
. That is
if it is holomorphic and
For any
and
we write
where
is the pseudo-hyperbolic metric and
.
Let
be an identity, we say
is a
-Carleson measure, if there is a constant
such that
for each
.
Now we define the dominanting set of Bergman spaces.
Lemma 1 Let
,
and G be a Lebesgue measurable subset of
. We call G is a dominanting set of
if there is a constant
such that
(1)
for all
.
Let
is the characteristic function of G. According to the definition of dominanting set, measure
satisfies the reverse inequality in Carleson measure definition, that is we have
for all
. We call reverse Carleson measure if the measure satidfy reverse Carleson inequality. The purpose of this paper is to study reverse
-Carleson measure. [1] and [2] provide some basic tools of Bergman space and some analytic functions. [3] proved Carleson-type embedding theorems for weighted Bergman spaces with Bkoll weights. In 1985, Luecking [4] first studied the reverse Carleson measure in Bergman space on unit disk. The main research tool of Luecking is the dominanting set in Bergman space. In [5] , Luecking introduces the necessary and sufficient conditions for dominating sets in Bergman spaces on a unit disk. In recent years, Lou and Zhuo [6] generalized this work to Fock space and gave the characterization of dominant set in Fock space. The purpose of this paper is to extend dominating set and reverse Carleson measure to weighted Bergman spaces. We can find some other concepts in [7] [8] [9] [10] [11] . [12] is a survey on reverse Carleson measures for various Hilbert spaces of analytic functions. We can use some definitions and proof methods in the paper to prove our results. [13] discussed direct and reverse Carleson measures for the de Branges-Rovnyak spaces
. We can refer to their method. In [14] , Korhonen and Rättyä has proved the sampling measure by using dominating set and p-Carleson measure for weighted Bergman space with a weight
, reference resources [15] [16] [17] [18] .
The main results is as follows.
Theorem 2 Suppose
. Then G is a dominanting set of
if and only if there are constant
and
such that
(2)
for all set
and all
.
In Section 2, we mainly give several key lemmas which can prove the main result. In Section 3, we prove the main theorem by using the lemma obtained in Section 2. Section 4 gives the conclusions of this paper and explains how to extend these results to other directions.
2. Preliminaries
In this section we collect several technical lemmas that we will need for the proof of our main result. We used the convention that the letter C denotes a constant which may differ from one occurrence to the next.
Lemma 3 (Exercise 1.1.3 (b) in) Let
be a Borel measure with
. We have
Lemma 4 (Lemma 1.24 in) For any real
and positive r there is constant
and
such that
for all
.
Lemma 5 (Lemma 2.20 in) For each
there is a positive constant
such that
and
for all a and z in
with
. Moreover, if r is bounded above, then we may choose
to be independent of r.
Lemma 6 (Corollary 2.21 in) Suppose
,
,
and
. Then there is a constant
such that
for all z and w in
with
.
Lemma 7 (Lemma 2.24 in) Suppose
,
and
. Then there is a constant
such that
for all
and all
. Moreover we can obtain
for all
where f is holomorphic and
is a constant independent of f and z.
If the analytic function
and
we consider the local level sets of f:
and the operator
where
is in Lemma 7.
By Lemma 7, we can get a inequality
We can use the same measure as in [5] to prove the following two Lemmas.
Lemma 8 Let f is analytic in
, there is a constant
in Lemma 7 such that
(3)
then
for all
.
Proof. Applying Lemma 7 and elementary estimates we have
where the last inequality follows by Lemma 3. If we subtract
from both sides we get
Then we have
We notice that
,
and
. Then we get
Lemma 9 Suppose
and
. Then let
for
and
. There is a constant C depending only on
, such that
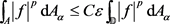
for all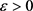 .
.
Proof. For 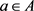 we have
we have
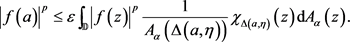
Integrate over 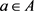 and use Fubini’s Theorem on the right to obtain
and use Fubini’s Theorem on the right to obtain
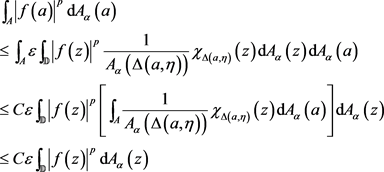
where the second inequality above follows from Lemma 6 and the fact that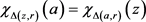 .
.
Lemma 10 Let 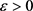 and
and 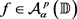 for
for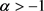 . Define the set
. Define the set
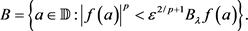
Then there is a constant C depending only on 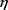 and p, such that
and p, such that
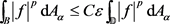
for all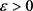 .
.
Proof. Let A be as in Lemma 9. We write
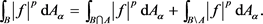
The first integral can be estimated by Lemma 9. For the second integral, we have
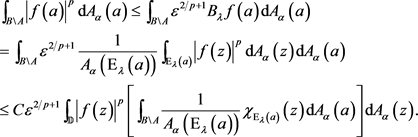 (4)
(4)
We need only show the inner integral is suitably bounded. The sets 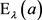 appeared in [5] , and Luecking proved in that paper that there is a constant
appeared in [5] , and Luecking proved in that paper that there is a constant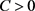 , depending only on p, such that
, depending only on p, such that
![]() (5)
(5)
Thus we can obtain
![]()
Combining this with inequality (5), we get
![]()
Plug this into (4) and use![]() . We obtain
. We obtain
![]()
3. Proof of Main Theorem
We can now characterize a special family of reverse Carleson measures for weighted Bergman spaces with the weighted Lebesgue measure. The main results is as follows.
Theorem 11 Suppose![]() . Then G is a dominanting set of
. Then G is a dominanting set of ![]() if and only if there are constant
if and only if there are constant ![]() and
and ![]() such that
such that
![]() (6)
(6)
for all set ![]() and all
and all![]() .
.
Proof. First, we proof the necessity of the Theorem. Take ![]() so that
so that
![]()
By a change of variables, we get
![]()
Then we can have
![]()
Applying (1) to the function
![]()
we get
![]()
Since![]() , so we have
, so we have
![]()
It is easy to verify that
![]()
Combining this with the above inequality, we get
![]()
so inequality
![]()
which gives (6).
For sufficiency of the theorem,we will follow the arguments in [5] closely. For ![]() let
let
![]()
According to Lemma 10, we have
![]()
If we now choose ![]() small enough so that
small enough so that![]() , we have
, we have
![]() (7)
(7)
By the definition of F we have ![]() for all
for all![]() .
.
If![]() , then
, then![]() . Lemma 8 can be write
. Lemma 8 can be write
![]()
For the ![]() in (6), we choose a positive integer
in (6), we choose a positive integer![]() , which implies that
, which implies that
![]() (8)
(8)
Therefore, by choosing
![]()
Lemma 8 gives
![]()
So we have
![]()
It implies that
![]()
Note that
![]()
then following from (6) we have
![]()
whenever![]() .
.
If ![]() so taht
so taht![]() , then
, then![]() . Lemma 8 can be write
. Lemma 8 can be write
![]()
Therefore, by choosing
![]()
Lemma 8 gives
![]()
So we have
![]()
It implies that
![]()
Note that
![]()
then following from (6) and (8) we have
![]()
whenever![]() .
.
Then we can get
![]()
for all constant ![]() in Lemma 7.
in Lemma 7.
Hence we have
![]()
![]()
where![]() . Integrating both side over F and using Fubini’s Theorem, we obtain
. Integrating both side over F and using Fubini’s Theorem, we obtain
![]() (9)
(9)
The integral in the brackets of the left-hand side can be estimated as follows:
![]()
And the right hand side of (9) can be estimated from below using (7). This yields
![]()
which proves the sufficiency of the theorem.
4. Conclusions
We proved the dominating set by using pseudo-hyperbolic metric disk and sub-mean inequality. The method of proof is to obtain the complete characterization of dominating set by applying the key lemma given in Section 2 in Section 3.
Next we will study some applications of Theorem 11. Let ![]() be a bounded measurable function on
be a bounded measurable function on![]() . So we want to prove that the Toeplitz operator
. So we want to prove that the Toeplitz operator ![]() is bounded. Using dominating set and Carleson measures, we can also study sampling measures for weighted Bergman space.
is bounded. Using dominating set and Carleson measures, we can also study sampling measures for weighted Bergman space.