A Parallel Processing Method for Moving Top-K Spatial Keyword Query ()
1. Introduction
In recent years, smart mobile devices represented by smartphones have not only been explosively developed in terms of quantity but also have greatly improved their processing capabilities and available network bandwidth. Smart mobile devices give users the ability to access information and services related to their current location anytime and anywhere. The rapid increase in the number of smart mobile devices enables governments and enterprises to provide users more and better location-based services (LBS) with high willingness. The increase in its processing power and communication bandwidth has made many previously unfeasible LBS applications possible [1] .
As an emerging service content in the current LBS field, Moving top-k Spatial Keywords (MkSK) query has been paid more and more attention. MkSK query provides mobile Internet users with search services of the spatial keywords results [2] [3] . For example, when a user visits a scenic spot, the mobile phone displays the information of the nearest attractions according to a current location in real time, and the user can set the screening conditions in advance so as to display only the type of attraction he is interested in. There are many works considering the problem [1] [4] [5] [6] .
The existing spatial moving k nearest keyword query algorithm usually considers only one factor of the position change of the queries, and its focus is on index optimization of the spatial relationship of the query object. The MkSK query not only needs to consider the relative position relationship between spatial objects but also consider the correlation between objects and query keywords. Keywords do not have the characteristics of continuous distribution similar to spatial positions, and they cannot be directly indexed by traditional spatial data structures (such as R*-tree). Therefore, the existing moving k nearest keyword query algorithm cannot be directly applied to MkSK query.
The current research on MkSK is mostly based on the safe area method. Literature [2] [3] combined with the related properties of Voronoi diagram, proposed the pruning strategy for space security area and cache-based query acceleration method. However, the query processing method based on the secure area is difficult to achieve the optimal update frequency and single update cost [4] . In addition, the existing MkSK processing methods are based on sequential calculation model, and it is difficult to effectively use the advantages of multi-core parallelism in large-scale servers.
To solve these problems, this paper proposes an MkSK query processing model based on impact set [4] and designs two query processing algorithms for server and client computer. The key part of the algorithm uses parallel technology to effectively improve the query efficiency. Experiments show that the proposed method outperforms the most advanced methods in both processing time and communication cost.
As far as we know, the method proposed in this paper is the first time that uses the impact set, and it is also the first time that concurrent mode is used to perform spatial moving k nearest keyword query processing.
In the following, we describe the keyword neighbors and their influence sets in Section 3, the algorithm in Section 4. We discuss the experimental results in Section 5 and conclude our work in Section 6.
2. Moving Top-k Neighbor Spatial Keyword Query
Given a set of objects D, each object
contains a pair of data
,
represents the location of the object
represents the keyword from the object. The spatial-keyword neighbor query
includes three parameters:
is the position of the query point,
represents query keyword,
is the number of query results, and the spatial-keyword neighbor query can be defined as follows:
Definition 1. (spatial keywords k nearest query) Given object set D and query
, spatial keyword neighbor query result set satisfies:
(1)
while
(2)
represents the weighted distances of q and
which takes into account the distance
between q and
, also considering the relevance of the keyword
.
The weight distance function
can be defined according to the needs, for example in the literature [2] :
, (3)
In the literature [3] :
(4)
The coefficient
is used to adjust the importance of the two parameters. This paper uses the definition of weight-distance in (5).
The TFIDF model [7] is a common correlation model, the model is defined as:
(6)
The function
represents the frequency of occurrences
in
, and the function
represents the reciprocal of the total number of objects
contained in D (Inverse Documlcwcent Frequency, IDF).
This paper uses TFIDF model to calculate the correlation between objects. In practical applications, we will modify (5) to
(7)
where c is a sufficiently small positive number, its presence makes
thus avoiding the divide-by-zero error in (3).
Figure 1 shows an example of a first-order Voronoi diagram based on a weight-distance function (3). When k = 1 and the keyword relevance
between the querier and each object is the value in parentheses after the object name, each small area separated by the curve in the figure corresponds to an object: in this small area, the querier’s keyword 1 nearest neighbor is this object.
The spatial-keyword k neighbor query is a single query, while the moving spatial-keyword k neighbor query is a continuous query:
Definition 2. (Moving top-k Spatial Keywords Nearest Neighbor Query) Moving top-k Spatial Keywords (MkSK) query is a process that continuously updates the query result N as
changes after given a data set D and initial query
. In this process, the elements in N always satisfy the constraint of
definition 1.
Moving top-k Spatial Keywords Nearest Neighbor Query is a kind of moving spatial neighbor query. In practical applications, the client-server architecture is often used to handle moving spatial neighbor queries. Clients are generally mobile devices with weak computing and storage capabilities, such as mobile phones, onboard computers, etc. The main computational operations and data storage rely on a powerful central server in the query process.
The simplest idea of dealing with moving spatial k neighbor queries is to recalculate N while each update of
. Due to the high computational cost and communication cost, this idea is obviously not feasible. At present, the main two categories of moving k neighbor query processing methods are based on the Safe Region (SR) and the Influential Set (IS) [4] .
1) Based on the Safe Region (SR)
This method calculates a security area for the current query result N. When the queryer q is located in the area, it can ensure that the result set N is correct. When the queryer q leaves the area, it needs to recalculate the N and the new security area.
The computational cost of this method includes a) the cost of determining the validity of the SR when the q is updated (the client) and b) the update cost of the SR (server).The SR update cost of the server is determined by the update frequency (recorded as sf) of the SR and the average calculation amount (recorded as sc) of each SR calculation recorded as
. Lowering the SR update frequency requires calculating a more accurate SR boundary, that is, lowering sf will increase sc. At the same time, lowering sc will make the security area inaccurate, and the area of the security area will inevitably become smaller in order to ensure correctness, thus increasing sf. Therefore, it is often difficult to optimize both sf and sc.
The literature [2] [3] separately proposed a moving top-k Spatial Keywords Nearest Neighbor Query method based on the security region according to different definitions of weight-distance functions (Equations (3) and (4)).
2) Based on the Influential Set (IS)
This method finds the object point pn with the largest distance from q in the current k-nearest neighbor query result set N, and the object point pi with the smallest distance from q in the effect set
of N. If and only if
, N is effective. The frequency of updating result sets in the method based on the impact set is always lower than the method based on the safe area. But the average calculation amount of each new calculation result set and its influence set can also be optimized through calculate the Voronoi diagram Without pre-calculated the keywords, so the overall efficiency is better than the method that based on the safe area [4] .
When performing keywords search, because of a large number of keywords and different Voronoi diagrams corresponding to different keywords, the keyword nearest neighbor query cannot be optimized using the pre-calculated Voronoi diagram.
As far as we know, there is no moving top-k spatial keyword nearest neighbor query based on impact set.
3. Keyword Neighbors and Their Influence Sets
First, we extend the definition of impact set [4] to the keyword moving neighbor query:
Definition 3. (Keyword Impact Sets) Given result set N of the keyword k nearest neighbor query when querying q and its initial position, the keyword impact set
of N is an object set, satisfying
, (8)
where
is that q’s keyword k nearest neighbor at the current position, and
. (9)
Without considering the keywords, querying the spatial k-nearest neighbors of the q can be found sequentially from the nearest to the far in the R*-tree [8] index by the Best-First [9] algorithm. However, when performing the keyword k nearest neighbor query, because the weight distance function
is affected by the keyword correlation, the keyword k neighbor set N of the query q is not necessarily distributed around the
, so it needs to (compared to k-nearest neighbor search that does not consider keywords) search within a larger range. At the same time, when the keyword of N is generated to affect the set IS(N), it also needs to expand the search range to ensure its correctness.
Determining N’s search scope is the first problem that must be solved for the keyword k nearest neighbor query. Theorem 1 points out that there exists a circular region with
as the center and the distance from
to the most distant object as the radius that may become the key K nearest neighbor. It is clear that the first k nearest neighbors of q are in this region.
Theorem 1. Given a set of objects D and a query q, consider any circle with a number of objects greater than k with
as the center, C is the set of all objects within the circle, and NC is the keyword k nearest neighbor set of q in C,
(10)
(11)
If
(12)
Then NC is equivalent to set N which q in the D’s keyword neighbor result.
Prove: To prove by contradiction. Suppose C is sorted by the weighted distance to q, the first k objects are not the keyword k nearest neighbors of q in D. That is if there is an object
is the keyword k neighboring of q in D but
does not belong to NC, then
(13)
The following discussion of the two conditions
and
, respectively.
1)
According to the definition of NC, there is,
(14)
Contradictions between Formula (15) and Formula (16).
2)
It is known from (13)
(17)
But it is known from (12)
(18)
It can be known from
and
,
, So
(19)
Known from (11)
(20)
Comprehensive (17)-(20) available
(21)
Contradictions between Formula (22) and Formula (23).
Synthesize the above 1 and 2 cases and get the proposition.
Theorem 1 indicates that there is a circular region in which the keyword k neighbor query result set of q is equivalent to the query result set in the entire space. Theorem 2 points out that we can find a minimal circular region that satisfies the condition of Theorem 1 by continuously expanding the radius.
Theorem 2. Given result set D and query q, investigate the circular area
which makes
as the center and r as the radius, when
, there is no object in this circle that satisfies the inequality in Theorem 1; when there is always an object in this circle that satisfies the inequality in Theorem 1.
Prove: The object set in the circle is C, and q’s keyword k neighbor result set of D is N,
(24)
Let
(25)
(26)
When
, it can be known from (27),
(28)
Combining (14) and (16) shows that there is no condition in C that the object satisfies the inequality in Theorem 1.
In summary, the proposition is established.
After generating the keyword k neighbor result set N of q, Theorem 3 limits the existence area of its keyword impact set IS(N). The object set of this region constitutes IS(N).
Theorem 3. Given the set of objects D and the query q, the q’s keyword k neighbors’ result sets that are recorded as N, using the definitions of (10), (11) and (26) for
and
, let
(29)
C is a set of all objects inside a circle that has a center around
with radius r, then
, (30)
Prove: Combining the definition of the impact set in [4] and the extended definition of the keyword impact set (Def. 3) in this paper, to prove that (30) is established, it is only necessary to prove that the set of neighbors of all objects of
in the key Voronoi diagram corresponding to
belongs to C, which is
(31)
where
represents the set of neighbors of the object p in the key Voronoi diagram corresponding to
.
To prove by contradiction. Suppose there is an object
and
(32)
According to the definition of Voronoi’s neighbors [10] , using a planar scanning method to perform a diffusion scan with
as the starting point will generate a base point event at
[9] , then
(33)
According to (17) there is
, at the same time
, so
(34)
which is
(35)
Combining (23) and (17) knows
and
contradicting.
Theorem evidence.
4. PMkSK Algorithm
According to the above theorem, this chapter proposes an algorithm based on the influence set of Parallel Moving top-k Spatial Keyword (PMkSK). Since the Voronoi diagram of the keyword cannot be pre-calculated, the efficiency of directly using the impact set method to process moving k spatial keyword will be very low. However, we observed there are no dependencies between the execution processes with large calculation amount in the process of calculating the impact set. We decompose these computational processes and design a parallel k-nearest neighbor and its influence set generation algorithm.
4.1. Algorithm Description
In the client-server architecture, the client first initiates a query to the server, the server generates a query result set N and it’s effect set IS(N) then return it to the client. The client verifies N's validity by constantly combining IS(N) with its current location when the location changes. If it is determined that N has expired, the request to the server is re-initiated and repeated until the user stops the query. For this kind of architecture, we separately designed the generating algorithm running on the server side for the computing keyword k nearest neighbor result set N and its influence set IS(N) and the verification algorithm running on the client side using IS(N)-to-N Verification.
4.1.1. Generation Algorithm
With
as the center of the circle, the scope of the circular search continues to expand until it finds the object
satisfying (15). According to Theorem 2, the keyword k-nearest neighbor of q in the circular region is the final query result N. From N and
, we can calculate the r-value in Equation (17), and then expand the search range to a circle with r as the radius,according to Theorem 3, the objects in this circle remove N and the rest of the object set is IS(N).
In the above process, when the circular search scope is expanded, multiple objects newly added in the circle can be judged and sorted in parallel. The algorithm uses the asynchronous parallel random access machine (APRAM) [10] model, accepts the query
and the data set D that has been indexed by IR-tree [11] (an improved R*-tree [8] , capable of indexing key data), then returns N and IS(N). The basic flow is shown in Algorithm 1.

In the algorithm, the linked list L can store spatial objects or MBR [8] at the same time. First, add the root MBR of IR-tree
to L. Then, the first element in was cyclically taken out in Best-First [12] way and updated L In the updated L the MBR containing
or (if there is no MBR containing
) most recent MBR with
or object are always ranked first. There are two different ways to update based on the type of elements that are taken from L.
1) If the retrieved element is an MBR, then the internal elements of the MBR are first sorted using a parity-ordering network [10] according to their distance from
(row 5, where par-do indicates that the subsequent statements can be executed in parallel) , and then sort the result of T by Batcher method [10] into L (line 6).
2) If the removed element is an object, remove it and put into the list C Objects in C are sorted in descending order of q weight-distance.
The CanTerminate(C) function calculates
from the first k-nearest neighbors that C already contains, and compares the distance between
and the first element in
and T. According to Theorem 2, it illustrates C already contains the first k nearest neighbors if
is small, so the loop can be ended. At this point, the first k elements in C are the result set N.
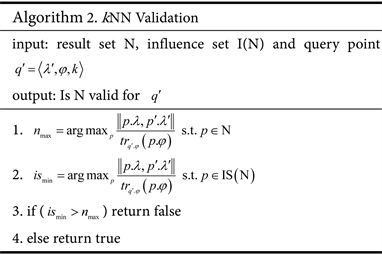
4.1.2. Verification Algorithm
Given a result set N, its impact set IS(N), and the moved query object
, according to definition 3, algorithm 2 can verify the validity of N to
according to IS(N).
4.2. Cost Analysis
4.2.1. Generation Algorithm (Algorithm 1)
Assuming the spatial keywords are evenly distributed, the regular Best-First algorithm requires a time complexity of
[9] . Algorithm 1 uses parity-ordered networks combined with Batcher merging and sorting methods to complete sorting in time
[10] (m indicates the number of sort objects, which is proportional to
and key distribution density), The required time is 1/m of the commonly used quick sorting algorithm(Its time complexity is
. Therefore, the time complexity of Algorithm 1 is
.
4.2.2. Authentication Algorithm (Algorithm 2)
The number of objects in the first and second rows is
, the time complexity required for taking the minimum and maximum values using the parallel balanced tree method is
(m is the number of objects) [13] , Therefore, the time complexity of Algorithm 2 is
.
5. Experimental Results
The experiment uses real position data sets HOTEL and GN. The data set details are shown in Table 1. The Brinkhoff [14] algorithm was used to generate the trajectories. Query keywords are randomly selected from keywords. The experimental platform uses Xeon E5-2640 six-core CPU and 8G memory.
The experiment uses the most advanced MSk-uvr moving keyword k nearest neighbor query processing method [2] to compare with the PMkSK algorithm of this paper. The default is set to k = 3 and the number of query keywords is 5.
Figure 2 shows the experimental results of the processing time varying with k. As can be seen from the figure, both the processing time and the communication cost of the two algorithms increase exponentially with the increase of k. However, the processing time and communication cost of the PMkSK algorithm in this paper is significantly less than that of the MSK-uvr algorithm. This is because the update method based on the impact set used by the PMkSK algorithm has a lower update frequency and less computational cost than the security area method used by the MSK-uvr algorithm. At the same time, the PMkSK algorithm uses parallel operations in the key steps of query processing, using multi-core processors to save the operating time.
Observing Figure 3, we can see that as the number of keywords increases, the processing time and communication cost required by the two algorithms increase, but the PMkSK algorithm of this paper is obviously better than the MSK-uvr algorithm. This is also because the PMkSK algorithm based on the impact set has lower update frequency and less computational cost than the MSK-uvr algorithm based on the safe area, and the parallel advantage of the PMkSK algorithm on the multi-core processor.
The above experimental results show that the PMkSK algorithm in this paper can take full advantage of parallel processing on a multi-core processor platform.
![]()
![]()
Figure 2. Processing time changes with k.
![]()
Figure 3. Processing time varies with the number of query keywords.
At the same time, because the PMkSK algorithm adopts an update verification method based on the impact set rather than the security area, its update cost and update frequency are better than the MSK-uvr algorithm.
6. Conclusion
A moving keyword k-nearest neighbor query processing method based on impact set is proposed, which avoids the inherent disadvantage of the update cost and update frequency cannot get excellent at the same time of the moving k nearest neighbor query processing method based on the security region. The parallel query algorithm is designed to calculate the k-nearest neighbor result set and obtain the influence set of the result set. The time complexity of the proposed server-side parallel query algorithm and client-side parallel verification algorithm is
existing method. The experimental results show that the parallel method proposed in this paper is more suitable for the multi-core servers and widely used than the existing methods for single-core systems.
Acknowledgements
This work is supported by the National Key R & D Program of China (2016YFC0801607), the National Nature Science Foundation of China (61872071, 61872070), the Fundamental Research Funds for the Central Universities (N171604008, N171605001), and the Ministry of Education Joint Foundation for Equipment Pre-Research (6141A020333).