Vane Shear Footing-Integrated Rational Approach for Seismic Bearing Capacity of Foundations & Seismic Pressure

B. Bikas Maiti, Dr. Ajayswarup

Department of Civil Engineering, Sri SathyaSai University of Technology and Medical Sciences, Sehore-Bhopal, India.

DOI: 10.4236/ojer.2019.82004                

Abstract

Structural buildings are subjected to huge cyclic powers during earthquakes. The structural failures during seismic events notably impact a variety of facets of buildings within tolerable levels like sustainable strength and stable energy dissipation capability to sustain inter-story drifts and overall structural damages. The major structural elements such as columns, beams and soil shearing capacities are majorly affected during seismic events. Buildings situated in the earthquake prone zone are exposed to most concerns in the structural design. Boreholes are also one of the main factors responsible for seismic waves and soil shearing. Shear strength is a term used in soil mechanics to describe the magnitude of the shear stress that soil can sustain, especially selected BC soil. The shear resistance of soil is a result of friction and interlocking of particles, and possibly cementation or bonding at particle contacts. Soils consist of individual particles that can slide and roll relative to one another. Shear strength of a soil is equal to the maximum value of shear stress that can be mobilized within a soil mass without failure taking place. In many parts of the world to avoid or control these consequences, buildings have been constructed as steel-composite structures. However, in India, buildings are being constructed as RCC framed structures. Here a novel combination of VANE shear footing and BRB method has been introduced. In this article, the effects of boreholes increase seismic bearing capacity of foundation, and load bearing capacity to balance seismic pressure.

Keywords

Earth Pressure Theory, Torque Moment (T), Soft Clay/Black Cotton Soil (BS-Soil), Buckling Restrained Braced (BRB), Passive Earth Pressure (PEP), Boreholes

1. Introduction

Most of the structural establishments are not having enough capacity to tolerate the seismic waves due to its design, and was probably not taken into consideration by the constructor during construction. These buildings are also not constructed with modern codes and prevalent earthquake resistance practice. Various dimensions of beams are available in the building on hilly slopes in the same storey. This attracts more waves during earthquakes and hence results in damage. Buildings located in the hills area and low soil shearing lands are different from buildings constructed in the plains. They are extremely sporadic and unsymmetrical in flat and vertical planes, and torsionally are coupled. Buildings of such qualities in the hills and low soil shearing are highly presumed to be suspicious to damage at the time of earthquake.

Buckling-Restrained Braces (BRBs) are a relatively recent development in the field of lateral load resisting structures. Brace is a generally late development in the field of parallel load opposing structures. Braced frameworks demonstrate high quality and sidelong solidness under moderate and furthermore in vast size seismic tremors. BRB design is to allow the building to withstand cyclical lateral loadings, typically earthquake induced loading. BRB Design flexibility in the selection of both stiffness and strength of the whole structural system of a building has been adapted. Clasping of steel prop is controlled and a similar quality is guaranteed both in pressure and tension.

A VANE shear footing with BRB method has been introduced in this paper. This method is currently being exercised to enhance the property of cohesiveness soil towards the system of the structure and to balance the passive vertical pressure. The VANE technique is used to improve shear strength through the system of soil “shear nailing”. Soil shearing limit and bearing limit needs to be focused on, for anticipated building against seismic waves. Along these lines, test directed and assessed the limit of the balance against feeble soil, and quake zone and conceivable outcome have been talked in this paper.

2. Study on Earthquakes and Seismic Waves

Seismology Ground Motion: Earthquake is being appeared when a sudden displacement of plates happen inside the earth. It released a portion of stored strain energy during this incident. It is called as seismic waves. These waves spread externally and across the surface of the earth. Since theses waves move faster it made ground motion and that is supposed as an earthquake. It shakes the ground and made cause the damage mostly. Fault burst can make significant harm yet it happens just close to the fault [1] .

Path Effects: The modification of the seismic wave field as it propagates through the complex crust of the earth has a strong, often dominant influence on strong ground motion. As a first approximation, the strongest variation of velocity with position in the earth is an increase in velocity with depth. In the earth’s crust, however, this assumption is often incorrect, particularly in the tectonically active environments in which earthquakes occur, because active tectonics naturally leads to complex geologic structures. During earthquakes, seismic waves become trapped and amplified by such basins, resulting in strong ground motion of long duration and strong spatial variation in amplitude, which can substantially increase the seismic forces on structures and lifelines. Moreover, near the edges of such basins, complex interference effects can greatly amplify ground motion relative to what it would have been in the absence of edges and basin effects [2] .

Wave Effects: Seismic waves are often referred to as elastic waves, but anelastic effects due to energy losses (interparticle friction), which give rise to the attenuation of seismic waves, cannot be neglected. The effect of attenuation on strong ground motion is profound, because the same soft materials near the earth’s surface that lead to strong amplification of ground motion can also lead to rapid attenuation. The net effect on the level of ground motion is complex because of elastic and anelastic effects. To predict strong ground motion, seismologists and engineers will have to characterize and account for an elastic wave effects in the earth’s crust. Again, research efforts in this area will probably require partnerships between NEES (Figure 1) and seismological research centers so that time-series data on an actual earthquake can be recorded as it occurs and made available for NEES experimental and testing purposes [3] .

3. Soil Shearing Strength

The shear strength of a soil is a function of the stresses applied to it and the manner in which these stresses are applied. Knowledge of shear strength of soils is necessary to determine the bearing capacity of foundations, the lateral pressure exerted on retaining walls, and the stability of slopes. Soil shear can give through foundations only for buildings. The three types of deep foundations one can come across are Pier foundation [4] , Pile foundation [5] and Well foundation [6] . But these all are failed when rising high rise buildings.

Soil Foundation Structure Interaction:

One sign of the connection that happens between a structure, its establishment, and the encompassing soil is the way that a vibrating structure can produce its very own seismic waves, which thus influence the free field ground movement. Truth be told, a few well-understood parts of soil structure collaboration, including the two connections depicted in what pursues are of essential significance

Figure 1. Nested linkages of activities and disciplines that NEES will bring to the resolution of earthquake engineering problem.

to quake engineering and engineering seismology. In the first place, the reaction to quake movement of a structure established on a deformable soil can be essentially not quite the same as the reaction of a similar structure on an inflexible establishment (shake), chiefly through an expansion in characteristic periods, an adjustment in the measure of framework damping because of wave radiation and damping in the dirt, and alteration of the successful seismic excitation. In specific cases, for substantial or prolonged structures like dams, structures with huge measurements and extensions, it might be alluring to know the spatial dissemination of the ground movement as opposed to the movement at a solitary area. Be that as it may, the advantages of such geologically exact information must be weighed against the expense of getting them. To show with more noteworthy unwavering quality soil establishment structure collaboration impacts amid solid tremors, coordinated models that join the structure, the encompassing soil and more reasonable, spatially disseminated seismic excitation must be created. This exertion will require close joint effort among specialists and seismologists. The participation of NEES in this area will be particularly advantageous. Figure 2 is representing the VANE shearing with BRB based concrete footing.

4. Earth Theory Pressure

Ground pressure (Figure 3) is the parallel weight applied by the clay on a shoring framework. It is reliant on the dirt structure and the association or development with the holding framework. Because of numerous factors, shoring issues can be very uncertain. In this manner, it is fundamental that great engineering judgment is utilized. In the season of seismic tremor the weight might happen from

Figure 2. VANE shearing with BRB based concrete footing.

any edge. At that time the contrary point will offer weight to the seismic waves. In view of seismic wave’s weight, the dynamic and inactive weight will contrast dependent on building weight (Active) and inverse weight of earth (Passive). Very still condition, dynamic earth weight will be there as consistency.

Active and passive earth pressures are the two phases of stress in soils which are specifically noteworthy in the plan or investigation of shoring frameworks. Dynamic weight is the condition in which the earth applies a power on a holding framework and the individuals tend to push toward the removal Figure 4.

Inactive pressure is a condition in which the holding framework applies a power on the clay Figure 5. Since soils have a more prominent latent obstruction, the earth weights are not the equivalent for dynamic and uninvolved conditions.

At rest lateral earth pressure, represented as $K_0$ , is the in situ horizontal pressure. It very well may be estimated by a dilatometer test (DMT) or a borehole pressure meter test (PMT). As these are fairly costly tests, experimental relations have been made with the end goal to anticipate very still weight with less included soil testing, and identify with the point of shearing obstruction. Two of the more regularly utilized are exhibited underneath.

For Normal consolidated soils:

$K_{0\left(NC\right)}=1-\sin {\phi }^{\prime }$ (1)

For Over consolidated soils:

$K_{0\left(OC\right)}=K_{0\left(NC\right)}\ast OC{R}^{\left(\sin {\phi }^{\prime }\right)}$ (2)

Figure 3. At-rest condition.

Figure 4. Active pressure.

Figure 5. Passive pressure.

The last requires the OCR profile with profundity to be resolved as follows:

Now and then earth weight characterized as the impartial side long earth weight or the horizontal earth pressure (Table 1) at solidified balance. The proportion of horizontal to vertical earth weight in this “no parallel strain” condition is named the coefficient of earth weight at $K_0={\sigma }_3/{\sigma }_1$ .

The at rest ground pressure coefficient (K₀) is relevant for deciding the in conditions of issues for undisturbed stores and for evaluating the dynamic weight in muds for frameworks with swaggers or shoring. At first, in light of the firm property of dirt, there will be no horizontal weight applied in the very still condition up to some tallness at the time the removal is made. Nonetheless, with time, creep and swelling of the earth will happen and a parallel weight will create. This coefficient considers the qualities of soil and will dependably give a positive horizontal weight. This strategy is known as the Neutral Earth Pressure Method [7] .

$K_0=\frac{v}{1-v}$ (3)

v = The poisson’s Ratio. It is determined by a Laboratory test (Maximum value = 0.5)

A Poisson’s ratio of 0.5 means, there is no volumetric change during shear (Completely undrained behaviour―Table 2).

Table 1. At rest earth pressure.

Table 2. Soil based Poisson’s ratio.

Vertical stress under corner of a Rectangular Area Carrying Uniform Pressure

The vertical stress at a depth z below the corner of a rectangular are subject to uniform pressure is,

$\Delta {\sigma }_z\left(\text{or}\Delta {\sigma }_z\right)=q\cdot I_R\text{or}q\cdot I_p$ (4)

$I_R=\frac{1}{\text{4π}}\left[\frac{2mn\sqrt{m^2+n^2+1}}{m^2+n^2+m^2{n}^2+1}\left(\frac{m^2+n^2+2}{m^2+n^2+1}\right)+{\tan }^{-1}\left(\frac{2mn\sqrt{m^2+n^2+1}}{m^2+n^2+m^2{n}^2+1}\right)\right]$ (5)

$\Delta {\sigma }_z=q\cdot I_p$

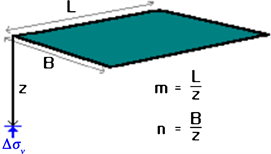
where

q is the bearing pressure

I_p is the influence factor

B: width of the loaded area

L: Length of the loaded area

For a Circular Loaded Area: The excess vertical stress (beneath centre)

$\Delta p=q\left[1-\frac{1}{{\left[{\left(R/2\right)}^2+1\right]}^{3/2}}\right]$ (6)

q is the uniformly distributed pressure on the circular area.

5. Soil Liquefaction

Quake instigated liquefaction includes soil misshaping caused by transient, monotonic or cyclic stacking and includes the age of overabundance pore water weight in soaked free union less soil under undrained stacking conditions. Liquefaction can be sorted into stream liquefaction and cyclic versatility and the disfigurements created by cyclic portability Failures grow incrementally amid seismic tremor shaking and driven by both static and cyclic shear stresses. Liquefaction potential at a specific soil site is impacted by the ground properties, the geology of the site, greatness of tremor influencing the site and the situation of the groundwater Table 3. It is fundamental for seaside areas to consider the liquefaction risk existing at the specific site not just from the past situations and current circumstances yet in addition that may happen from the future patterns.

Bearing limit examinations of all the 12 boreholes at a profundity of 1.5 m have been actualized. The greatness of union and point of frictional opposition at a profundity of 1.5 m have been gotten from soil examination reports given by different counselling firms and organizations. The groundwater level is observed to be at a profundity past 6.4 m underneath ordinary ground level for all the boreholes as given in the dirt examination report. 3 distinctive establishment widths are 1.5 m, 3 m and 4.5 m have been considered for deciding the bearing limit of the ground at 1.5 m profundity. The net admissible bearing weight as given in the dirt examination report is 90 kPa. It might be noticed that a base factor of security of 2.5 is wanted against bearing limit failures for static examinations while for seismic investigations the coveted factor of protection is 1.875 as obtained from IS 1893―Part 1.

The issue of soil liquefaction building establishment over seismic tremor shaking because of high bore water weight in approximately pressed sand stores situated underneath the groundwater Table 3, prompting huge misfortune in shear quality and making it stream like a thick liquid, is a serious worry for civil architects. In the present examination, liquefaction weakness under seismic tremor conditions has been registered for 12 boreholes till a profundity of 9m at a dirt site in India (Table 3). The said site goes under seismic zone III according to Indian seismic plan code IS 1893―Part 124 and henceforth an outline quickening of 0.16 g was considered for the building plan. The seismic speeding up coefficient was additionally registered according to Eurocode EN1998―Part 519 and examination in liquefaction weakness was done for the dirt site. This was trailed by calculation of seismic bearing limit and the factor of safety (Table 4) at a profundity of 1.5 m subterranean surface for the proposed building establishment. (Notification: Non-liquefying―NL, Yellow brown clayey sand silt―YBCSS, Grey silty sand―GSS, Grey brown sandy clayey silt―GBSCS, Will not liquefy―WNL, Will liquefy―WL, Safe―s, Not Acceptable―NA)

Table 3. Status of liquefiable strata for the 12 boreholes considered in the present study.

Table 4. Calculation of factor of safety against static and seismic bearing capacity for different foundation widths for the 12 boreholes.

$\text{Value}\text{of}{K}_h\left(\text{EN1998}\right)=0.25$

$\left(\text{IS}:1893\right)=0.16$

$\frac{K_h\left(\text{EN}\right)}{K_h\left(\text{IS}\right)}=1.56\text{times},\text{Comparison between unequal zone factors}{K}_h$

In light of the results (Table 5 & Table 6), it was seen that some specific boreholes demonstrated vulnerability to liquefaction at specific profundities under quake shaking. In addition, a portion of the chose boreholes are observed to

(a) (b)

Table 5. (a) Bearing capacity factors for static and seismic analysis for different widths of foundation in borehole 1; (b) Factor of safety against bearing capacity failure under static and seismic conditions for different widths of foundation in borehole 1.

(a) (b)

Table 6. (a) Bearing capacity factors for static and seismic analysis for different widths of foundation in borehole 6 according; (b) Factor of safety against bearing capacity failure under static and seismic conditions for different widths of foundation in borehole 6.

be inclined to bearing limit failure at 1.5 m profundity according to Eurocode EN1998―Part 519 for specific establishments. Thus the proposed results demonstrate the requirement for such investigation with future suggestions of therapeutic measures for the safe outline of building establishments at the site under tremor conditions.

6. VANE Shearing Footing (VSF)

The effects of forces spread over a large surface area

What you measure is the way the ordinary power (a power opposite to the surface a protest is sliding on) identifies with the grating power. Things being what they are, to a decent level of exactness, the two powers are corresponding, and you can utilize a constant,

$\mu$

To relate the two:

$F_{\text{friction}}=\mu F_{\text{normal}}$

or

$F_F=\mu F_N$ (7)

This equation defines the normal force, $F_N$ , multiply all it by a constant to get the friction force, $F_F$ , this constant, $\mu$ is called the coefficient of friction and it measures between two particular surface. Relates the magnitude of the force of friction to the magnitude of the normal force. The normal force is always directed parallel to the surface. $F_F$ and $F_N$ are always perpendicular to each other.

The power because of rubbing is for the most part free of the contact zone between the two surfaces. This implies regardless of whether you have two substantial objects of a similar mass, where one is half as long and twice as high as the other one, despite everything they encounter the equivalent frictional power when you drag them over the ground. This bodes well, provided that the region of contact pairs, you may feel that you ought to get twice as much grating. In any case, when you twofold the length of a question, you divide the power on each square centimeter, in light of the fact that less weight is above it to push down. Note that this relationship separates when the surface territory gets too little, from that point forward the coefficient of grinding increments in light of the fact that the question may start to dive into the surface. Pressure is characterized as the power applied on a surface partitioned by the zone over which that power acts.

$\text{Pressure}=\frac{\text{Force}}{\text{Area}}=\frac{F}{A}$ (8)

This equivalent strategy utilizing in VANE shearing balance (Figure 7 & Figure 8), the balance technique was outlining dependent on VANE show in Figure 6 and four wings are there to balance the shear stress more than column height. According to the exchange of weights and power/region will adjust the seismic waves from auxiliary sides. The dynamic weight will be in the focal point of the VANE shear balance. Building weight just connected as Torgue. Seismic waves will assault the nails of the VANE shear balance. Nails of the balance stature and width proportion ought to be with 2:1.

$\sigma =M/2\text{π}{R}^{2}L$

$R_0>R_1{\left({\sigma }_{YB}/{\sigma }_{YW}\right)}^{1/2}$ (9)

$\text{Surface}\text{area}\text{of}\text{the}\text{cylinder}=2\text{π}rh=\text{π}dh$

$T=M_s+M_e+M_e=M_s+2M_e$ (10)

$C_u=\frac{T}{\text{π}\left(\frac{d^{2}h}{2}+\frac{3d^3}{20}\right)}$ (11)

Figure 6. VANE shear footing system.

Figure 7. Vane shear test for balancing and distributing force.

Figure 8. Assuming a parabolic distribution of shear strength (M_e).

Vane shear test: After the underlying test, vane can be quickly turned through a few unrests until the point when the dirt moves toward becoming remolded. Since the test is quick, Unconsolidated Undrained (UU) can be normal.

$\text{Sensitivity}=\frac{\text{Peak Strength}}{\text{Ultimate Strength}}$

The accompanying outcomes have shaped a progression of vane shear test completed a site (Table 7). Plot the undrained shear quality versus profundity profile. Plot ought to have profundity on the vertical pivot with zero (Figure 9) at the highest point of the plot $\tau$ .

Figure 9. Peak and ultimate strength.

Table 7. Dimension of the column and wings size (feet into mm).

Observations and calculation of Torque:

$T=\varnothing \ast K/180$

where, T = Torque

∅ = Difference of angle (angle of Torque)

K = Spring factor

Calculate shear strength: Shear strength of the soil, C is computed using the following formula,

$T=C{\pi }^{*}\left[\left(d^{2}h/2\right)+\left(d^3/6\right)\right]$

where,

D = Diameter of vane (cm)

H = Height of vane (cm)

C = Shear strength (kg/cm²)

T = Torque applied (kg-cm)

7. PEP with BRB Load Bearing Capacity

The soil characterization and configuration stack bearing limit will have appeared on the construction reports (Table 8). Where required by the magistrate, the specialist in charge of the examination will sign, seal and present a composed report of the examination that incorporates, yet require not be restricted to the below data: Suggestions for establishment compose and plan criteria, including yet not restricted to bearing limit of regular or compacted soil; relief of the impacts

Table 8. Presumed allowable bearing pressure (kPa).

of liquefaction; differential settlement and fluctuating soil quality and the impacts of nearby loads Expected aggregate and differential settlement; Pile and Pier establishment proposals and introduced limits Special outline and construction arrangements for footings or establishments established on extensive soils, as important Compacted fill material properties and testing as per area 1803.5.

Note:

1) Use ${\gamma }_d$ for all cases without water. Use ${\gamma }_{sat}$ for calculations with water. If simply density is mentioned use accordingly

2) Fill all the available data with proper units

3) Write down the required formula

4) If the given soil is sand, c = 0

BRB: To maintain a strategic distance from failures of the open ground story in the regular case engineers consider an alternate material with enough stretching limit that would be steel with that limit. The normal BRB appears in Figure 10. It frames an astounding structure by high level of malleability. The cyclic character of steel supports at some point will be turned around. The compressive and pliable power of steel uncovers ease back vitality decadence because of the clasping of the prop when the heap on the steel builds the breaking point of clasping.

The over quality sources like strain solidifying makes columns and beams to be measured interestingly to oppose powers identified with the normal quality of supports. On the off chance that prop should be in compressions some unique material like unbinding material put in the middle of the infill and center part concrete is required to definitely diminish the contact on supports. The advantages of BRB are collected by designers as it is little in part sizes, for instance, its segment and shafts and lower request on establishments particularly the emerging pressure loads are amazingly diminished. It gives designs a bigger proficient plan region of the building, which likewise expands the land value [8] .

Basics of BRB:

Gross pressure intensity (q)

Net pressure intensity (q_n)

$q_n=q-\gamma D$ (12)

Ultimate bearing capacity (q_f)

Net ultimate bearing capacity (q_nf)-minimum net pressure

$q_{nf}=q_f-\gamma D$ (13)

Net safe bearing capacity (q_ns)-maximum net pressure

Figure 10. Buckling restrained braced frames.

Table 9. Result Discussion with VSF and BRB.

$q_{ns}=\frac{q_{nf}}{F}$ (14)

F = shear failure.

Safe bearing capacity (q_s) is the gross pressure

$q_s=\frac{q_f}{F}$

or

$q_s=q_{ns}+\gamma D$

$q_s=\frac{q_{ns}}{F}+\gamma D$ (15)

Bearing pressure (q_a), shear failure and excessive settlement structure is $q_a=q_{na}+\gamma D$ , where, q_na = net allowable bearing pressure.

BRB demonstrates a symmetry in the reaction over the activity of sidelong loads and BRB is designed so that the clasping during the pressure cycle is maintained a strategic distance. BRB have a steady power twisting bend over strain and pressure cycle while concentric support performs well amid strain cycle and encounters clasping amid the pressure cycle. After the clasping of the prop, the support failures its quality and prompts the break of the prop in the resulting cycles. Low pressure cycle limit prompts the low vitality scattering and disfigurement malleability of the support when contrasted with the BRB.

8. Conclusion

This study analyzed both boreholes impacts and the behaviour of VSF and BRB. The VSF + BRB (Table 9 and Figure 2) methodology adopted for this experiment is scaled by trigger voltage. The geometrical properties are simulated by shaking table test and exerting direct shear of velocity after and before testing. These test results are compared with previous tests [1] [2] ; this VSF + BRB shows better results to protect buildings from seismic waves.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Bikas Maiti, B. and Dr. Ajayswarup (2018a) Fan Footing Soil Foundation to Safeguard High and Low Rise Buildings from Seismic Waves. International Journal of Advanced Engineering Research and Science (IJAERS), 5, 11-21.
[2]	Bikas Maiti, B. and Dr. Ajayswarup (2018b) Applying Tripod Footing in Base Foundation to Act an Base Isolation System to Reduce the Seismic Action against Failure. International Journal of Civil Engineering and Technology (IJCIET), 9, 761-771.
[3]	Lin, S.-L., Li, J., Elnashai, A.S. and Spencer Jr., B.F. (2012) NEES Integrated Seismic Risk Assessment Framework (NISRAF). Soil Dynamics and Earthquake Engineering, 42, 219-228. https://doi.org/10.1016/j.soildyn.2012.06.005
[4]	Butchibabu, B., Sandeep, N., Sivaram, Y.V., Jha, P.C. and Khan, P.K. (2014) Bridge Pier Foundation Evaluation Using Cross-Hole Seismic Tomographic Imaging. Journal of Applied Geophysics, 144, 104-114. https://doi.org/10.1016/j.jappgeo.2017.07.008
[5]	Tomisawa, K. and Kimura, M. (2017) New Technology on Seismic Reinforcement of Pile Foundation for Long Life Bridges. Procedia Engineering, 171, 1035-1042. https://doi.org/10.1016/j.proeng.2017.01.443
[6]	Chowdhury, I., Tarafdar, R., Ghosh, A. and Dasgupta, S.P. (2017) Dynamic Soil Structure Interaction of Bridge Piers Supported on Well Foundation. Soil Dynamics and Earthquake Engineering, 97, 251-265. https://doi.org/10.1016/j.soildyn.2017.03.005
[7]	Chen, K.-H. and Peng, F.-L. (2018) An Improved Method to Calculate the Vertical Earth Pressure for Deep Shield Tunnel in Shanghai Soil Layers. Tunnelling and Underground Space Technology, 75, 43-66. https://doi.org/10.1016/j.tust.2018.01.027
[8]	Bosco, M., Marino, E.M. and Rossi, P.P. (2015) Design of Steel Frames Equipped with BRBs in the Framework of Eurocode 8. Journal of Constructional Steel Research, 113, 43-57. https://doi.org/10.1016/j.jcsr.2015.05.016