Active Control of Chaotic Oscillations in Nonlinear Chemical Dynamics ()
1. Introduction
Since the discovery of chaos in the 20th century, the chaos has been recognized as a very interesting behavior in nonlinear dynamical systems [1] [2] [3] [4] ; according to the domain, it is sometimes useful [5] or undesirable. The control from this chaos in nonlinear oscillations became a very important concern for scientists because of its multiple applications in various fields such as Physics, Chemistry, Biochemistry, Biology, etc. [6] - [11] . In nonlinear systems, several types of movement can be obtained, depending on the nature of the non-linearity, the choice of parameters and initial conditions considered. For potential applications, it has been found necessary to control or eliminate chaotic oscillations in some systems. In order to achieve this goal, several control techniques such as passive, active and semi-active controls are chosen and used according to the nature of the problem considered. An exhaustive review of the description and most important results of active control are given in Refs [9] [12] - [19] . In-depth study using passive control technique is done on nonlinear chemical systems and the most important results are given in Ref. [10] . The class of nonlinear chemicals reactions considered is that of Belousov-Zhabotinsky (BZ). The nonlinear oscillations of the chemical reactions of BZ can be modeled by a modified Van der Pol-Duffing oscillator [20] . Our goal in this work is to make active control of nonlinear oscillations of this class of chemical reactions of BZ by coupling the Forced modified Van der Pol-Duffing oscillator to a linear oscillator [13] which will be used as a control element. The organization of this paper is as follows: Section 2 presents the mathematical modeling of nonlinear chemical oscillations influenced by external sinusoidal excitation under an active control process. In Section 3, Lindstedt’s perturbation method and harmonic balance method are used to determine respectively the analytical solution of the modified Van der Pol-Duffing oscillator and the amplitude of the oscillatory states of the system under control. The effects of the constraint parameter β and the control parameter λ on the amplitude of oscillations are also presented. Section 4 discusses the effects of the active control process on the chaotic dynamic states of the system. The conclusion is presented in the last section.
2. Model and Equation of Oscillations
This work takes into account all nonlinear chemical systems as a kinetic example which can be described by the following equations [1] [21] [22]
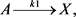 (1)
(1)
 (2)
(2)
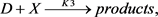 (3)
(3)
 (4)
(4)
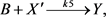 (5)
(5)
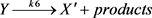 (6)
(6)
When we assume that the sink of the product is a first order reaction and we base ourselves that the laws of mass action and conservation, we get after some mathematical transformations that the self-oscillations in some nonlinear chemical systems can be modelised by the following single second order differential equation [10] - [20] :
 (7)
(7)
where 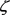 is proportional to the concentration of species X and represents the displacement.
is proportional to the concentration of species X and represents the displacement. 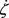 and
and 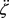 are the velocity and acceleration respectively. Parameters µ, α and γ respectively denote the damping coefficient, linear and cubic nonlinear restoring parameters. The nonlinear parameter β mark the difference between the oscillator equation Equation (7) and the equation of classical Van der Pol-Duffing oscillator. Many dynamic behaviors are obtained when the system is subject to an external sinusoidal excitation [20] and in this case the dynamics of the model is modeled by the following equation:
are the velocity and acceleration respectively. Parameters µ, α and γ respectively denote the damping coefficient, linear and cubic nonlinear restoring parameters. The nonlinear parameter β mark the difference between the oscillator equation Equation (7) and the equation of classical Van der Pol-Duffing oscillator. Many dynamic behaviors are obtained when the system is subject to an external sinusoidal excitation [20] and in this case the dynamics of the model is modeled by the following equation:
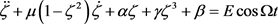 (8)
(8)
It has been noticed the presence of chaotic behaviors of this model [20] . Our main objective of the work is to limit the undesirable effects of external excitation by using the active control strategy. To achieve this goal of reduce the amplitude of the vibration and suppress nonperiodic movements in the model given by Equation (8), we use the following linear oscillator [13] for control element:
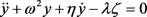 (9)
(9)
where y is the control force and λ the control gain parameters, ω the free frequency of the linear oscillator and η the damping coefficient. Accordingly, the equation of the nonlinear chemical system under such a control scheme becomes:

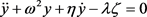 (10)
(10)
3. Effects of the Control on the Amplitude of Harmonic Oscillations
Without the external sinusoidal excitation force, Equation (7) is solved using the Lindstedt’s perturbation method [23] [24] [25] . We get that the solution of Equation (7) can be approached by:
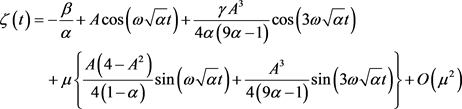 (11)
(11)
where the frequency ω is given by
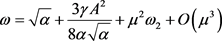 (12)
(12)
and
 (13)
(13)
With the external sinusoidal excitation force, assuming that the fundamental component of the solutions has the period of the external excitation, we express the solution ζ as follows:
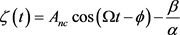 (14)
(14)
To determine the amplitude of the vibration of the chemical system under control, we use the harmonic balance method [25] . For this fact, we introduce the expression of ζ defined by Equation (14) in the second equation of the system of Equations (10) and we get the following:
![]() (15)
(15)
with
![]()
![]()
![]()
Then, inserting the Equation (15) in the first equation of the system of Equations (10) gives us:
![]() (16)
(16)
When we introduce the expression (14) in Equation (16) and equalize the coefficient of the terms in sinus and cosine, we obtain after a few algebraic manipulations the following differential equation satisfied by the amplitude Ac of the oscillatory states
![]() (17)
(17)
It is noted that control is effective when amplitude Ac of vibration of the system under control is lower than amplitude Anc of oscillations of the uncontrolled system obtained for λ = 0. We determine the domain of the parameter of control λ for which control is effective by solving Equation (17) with the Newton-Raphson algorithm. The amplitude Ac obtained from this resolution is plotted on Figure 1 by varying the control parameter λ. It appears from this plot that the control is effective for ![]() when β = 0.008;
when β = 0.008; ![]() when β = 0.3 and
when β = 0.3 and ![]() when β = 0.4. The behavior of the amplitude Ac is also observed when the amplitude of the external excitation E is varied. The existence of the phenomenon of hysteresis and of the jump amplitude of the harmonic oscillations has been noticed in the system under control. We notice the disappearance of these phenomena with the increase of the control parameter λ (see Figure 2) and also with the increase of the constraint parameter β (see Figure 3). We therefore retain that the control parameter λ and the constraint parameter β can be used to effectively control the phenomena of hysteresis and jump amplitude of the harmonic oscillations in some nonlinear chemical systems.
when β = 0.4. The behavior of the amplitude Ac is also observed when the amplitude of the external excitation E is varied. The existence of the phenomenon of hysteresis and of the jump amplitude of the harmonic oscillations has been noticed in the system under control. We notice the disappearance of these phenomena with the increase of the control parameter λ (see Figure 2) and also with the increase of the constraint parameter β (see Figure 3). We therefore retain that the control parameter λ and the constraint parameter β can be used to effectively control the phenomena of hysteresis and jump amplitude of the harmonic oscillations in some nonlinear chemical systems.
![]()
Figure 1. Effects of the control on the amplitude of the oscillations for different values of β with the parameters µ = 0.0001; α = 1; γ = 0.5; E = 0.03; η = 0.2 and Ω = ω = 1.
![]()
Figure 2. Effects of the control parameter λ on the amplitude-response curve displaying jump in amplitude Ac(E) with the parameters µ = 0.045; α = 0.15; γ = 0.5; β = 0.008; η = 0.2; Ω = ω = 1.
![]()
Figure 3. Effects of the parameter β on the amplitude-response curve displaying jump in amplitude Ac(E) with the parameters λ = 0.25; η = 0.2; ω = 1 and the other parameters of the Figure 2.
4. Effects of the Control on the Chaotic Oscillations of Model
The conditions for suppressing chaotic oscillations or instabilities in the modified and forced Van der Pol-Duffing oscillator coupled to the considered linear oscillator are investigated by doing the numerical simulation of the Equation (10). Figure 4 and Figure 5 illustrate the effects of the coupling parameter λ on the bifurcation structure when E et β vary respectively. We notice the appearance of different structures of bifurcation on each of these figures when the coupling parameter varies. Figure 4 shows periodic, quasiperiodic and chaotic movements for![]() ; periodic and chaotic movements for λ = 1.20 and periodic oscillations for λ = 1.705. Figure 5 shows periodic, quasiperiodic and chaotic movements for
; periodic and chaotic movements for λ = 1.20 and periodic oscillations for λ = 1.705. Figure 5 shows periodic, quasiperiodic and chaotic movements for![]() ; periodic and quasiperiodic movements for λ = 0.28 and periodic oscillations for λ = 0.40. Figure 6 shows the effect of the constraint parameter β on the bifurcation structure when the control parameter λ varies. We notice the appearance of the undesirable effects when β becomes big. By representing the phase portraits and its corresponding Time history (see Figures 7-9) of the system under control using the system of Equations (10), we checked the predictions of bifurcation diagrams. A confirmation of the predictions of bifurcation diagrams is thus obtained. We therefore note that for a given set of model parameters when the control parameter evolves, the undesirable oscillations of the oscillator pass to periodic oscillations and also, the control is more effective in chemical dynamics for low values of β.
; periodic and quasiperiodic movements for λ = 0.28 and periodic oscillations for λ = 0.40. Figure 6 shows the effect of the constraint parameter β on the bifurcation structure when the control parameter λ varies. We notice the appearance of the undesirable effects when β becomes big. By representing the phase portraits and its corresponding Time history (see Figures 7-9) of the system under control using the system of Equations (10), we checked the predictions of bifurcation diagrams. A confirmation of the predictions of bifurcation diagrams is thus obtained. We therefore note that for a given set of model parameters when the control parameter evolves, the undesirable oscillations of the oscillator pass to periodic oscillations and also, the control is more effective in chemical dynamics for low values of β.
5. Conclusion
In this paper we have investigated the active control of chaotic oscillations in certain nonlinear chemical dynamics. We have considered chemical dynamics modeled by a modified Van der Pol-Duffing oscillator subjected to external periodic
![]()
Figure 4. Effects of the control on the bifurcation diagrams showing the variation of the variable ζ versus the amplitude E for (a) λ = 0; (b) λ = 0.15; (c) λ = 1.20; (d) λ = 1.705 with the parameters µ = 0.0001; α = 1; γ = 0.5; β = 0.008; η = 0.2 and Ω = ω= 1.
![]()
Figure 5. Effects of the control on the bifurcation diagrams showing the variation of the variable ζ versus the parameter β for (a) λ = 0; (b) λ = 0.20; (c) λ = 0.28; (d) λ = 0.40 with the parameters µ = 0.0001; α = 1; γ = 0.5; η = 0.2; E = 0.03 and Ω = ω = 1.
![]()
Figure 6. Effects of the parameter β on the bifurcation diagrams showing the variation of the variable ζ versus the control parameter λ for (a) β = 0.008; (b) β = 1.5; (c) β = 5 with the parameters µ = 0.0001; α = 1; γ = 0.5; η = 0.2; E = 0.03 and Ω = ω = 1.
![]()
Figure 7. Various phase portrait (left) and its corresponding times histories (right) for (a) (b) λ = 0; (c) (d) λ = 0.15; (e) (f) λ = 1.20; (g) (h) λ = 1.705 with the parametersµ = 0.0001; α = 1; γ = 0.5; β = 0.008; E = 24; η = 0.2; and Ω = ω = 1.
![]()
Figure 8. Various phase portrait (left) and its corresponding times histories (right) for (a) (b) λ = 0; (c) (d) λ = 0.20; (e) (f) λ = 0.28; (g) (h) λ = 0.40 with the parameters µ = 0.0001; α = 1; γ = 0.5; β = 0.5; E = 0.03; η = 0.2 and Ω = ω = 1.
![]()
Figure 9. Various phase portrait (left) and its corresponding times histories (right) for (a) (b) β = 0.008; (c) (d) β = 1.50; (e) (f) β = 5 with the parameters µ = 0.0001; α = 1; γ = 0.5; E = 0.03; η = 0.2; Ω = ω= 1 and λ = 0.75.
excitation. The model has been described and the corresponding equation presented. The Lindstedt’s perturbation method is used to find an analytic solution of the modified Van der Pol-Duffing oscillator. The amplitudes of the oscillatory states of the system under control have been found using the harmonic balance method. In the dynamics of the model under control, we noticed the appearance of the phenomena of hysteresis and jump amplitude, which is effectively controlled by the control parameter λ and the constraint parameter β. Active control is used to limit the presence of unwanted behaviors in the system. We have found the appropriate coupling parameter for which the linear oscillator effectively reduces the amplitude of the modified Van der Pol-Duffing oscillator. For a set of fixed values of the model parameters it was noted that the chaotic behavior of this oscillator has given way to periodic movements under the effect of active control.
Acknowledgements
The author thanks IMSP-UAC, DAAD for financial support and the anonymous referees whose useful criticisms, comments and suggestions have helped strengthen the content and the quality of the paper.