The Effect of Ethanol on the Transport of a Neutral Amino Acid in the Perfused Whole Human Placenta ()
1. Introduction
The placenta is the site of absorption and transfer of nutrients for fetal growth and development. In addition, it metabolizes nutrients for its own use [1] and performs a number of other regulatory and biochemical functions [2]. The primary role of the placenta is to transport nutrients to the fetus and to remove toxic wastes from the fetus. Perhaps the most critical nutrients for fetal development are the amino acids, since they are the building blocks of the body’s proteins. Many of them have been shown to be transferred to the fetus by active transport against a substantial gradient with the expenditure of metabolic energy [3 , 4]. Biochemical studies give evidence that protein calorie malnutrition impairs the energy metabolism in the cells by interfering with the synthesis of deoxyribonucleic acid (DNA) and enzymes involved in glycolysis and the citric acid cycle. Without adequate supplies of amino acids and energy, cell functions break down, and normal processes of growth cannot occur. The effects would be most damaging when cells are normally undergoing rapid division [5]. The human placenta increases in weight until shortly before term. By contrast, the total number of cells (DNA content) reaches a maximum at around 34 weeks gestation. Any stimulus which retards fetal growth before 34 weeks should result in a smaller placenta with fewer cells. In addition any stimulus beginning early and lasting throughout pregnancy would be expected to result in a placenta with both reduced cell number and reduced cell size [6 , 7]. Ethyl alcohol or ethanol is a teratogen readily transported across the placenta. The fetus, of course, depends completely on the placenta and maternal blood for all of the necessities of life. Because of this, chemicals such as ethanol may affect fetal nutrition by having an effect primarily on the placental metabolism [8] and secondarily on the placental transport processes [9]. It is not ethically possible to examine nutrient transport directly in humans. Consequently, work toward understanding how maternal nutrition influences growth and development of the fetus usually has been done on animals such as the rat, the guinea-pig, and the sheep. However, in vitro perfusion techniques [10] provided that they simulate closely enough the in vivo conditions, do eliminate ethical and safety concerns as well as provide a simplified and well controlled experimental model.
Although qualitative and quantitative differences probably exist between placentas at different stages of pregnancy, the term placenta (which is one of the rare human organs readily available for the in vitro study) can serve as a valid tool for the study of nutrient transport [11], as long as experiments are done carefully.
In this study, experimental results from the perfusion of the whole human placenta at term were presented with the purpose of understanding the transplacental transport of amino acids in the absence or presence of ethanol, using a non metabolizable amino acid analog (
-amino isobutyric acids: AIB). A one-dimensional mathematical model with three compartments was also constructed to characterize the amino acid transport mechanism in the human placenta.
2. Background
2.1. Techniques for Placental Transport Study
The inaccessibility of the human placenta in pregnancy effectively excludes any direct examination of its transfer function, and although animal models have contributed greatly to a general understanding of placental function there are major interspecies differences, and similarity of behavior with humans can never be assumed. The obvious alternative is to exploit the placenta when it becomes available after delivery, but that portion presents great technical difficulties [12]. The various techniques generally used for the placenta are listed in Table 1.
2.2. Transport of AIB in the Placenta
Placental nutrient transport plays a vital role in the development of the embryo and fetus. In humans, the placenta and fetal circulation form during the early weeks of embryonic life. The placenta then continues to develop, growing in size, changing morphologically, and altering transport activities until at term it weighs about one seventh that of the fetus. Although substances can move between maternal and fetal circulations via the amnion or the yolk sac, near term the chorionic membranes probably account for the majority of total nutrient transport. Table 2 summarizes the classes of substances crossing the placenta
![]()
Table 1. Placental tissue preparations in vitro.
![]()
Table 2. Transplacental mechanisms.
and the mechanisms believed to be responsible for their transport [18 , 19]. Extensive reviews about the transport of amino acids were reported by Yudilevich and Sweiry (1985).
There are two mechanisms for the movement of amino acids across the placenta: active transport and passive diffusion [20]. For active transport several lines of evidence may be cited: 1) concentrations of amino acids in fetal plasma are greater than in maternal plasma, 2) placental transfer of amino acids against this concentration gradient has been demonstrated in the isolated guinea pig placenta [21 , 22], in the in situ perfused guinea pig placenta [15], and in the in vitro dually perfused placentas of human [20 , 23], 3) placental tissue slices and fragments actively concentrate amino acids against a concentration gradient [3 , 20 , 24 - 26].
Neutral amino acids can be concentrated in both the trophoblast and fetal blood. This concentration is stereo specific and energy dependent. The neutral amino acid,
-amino isobutyric acid (AIB), has been a useful marker for the characterization of these amino acid transport processes in the placenta because it is not metabolized. Because of this fact, AIB has been frequently used as an analog for naturally occurring amino acids [3 , 26 , 27]. AIB is known to be non-metabolizable, energy dependent, saturable, and transported in the same glutamine [25]. The molecular structure of AIB is shown as below:
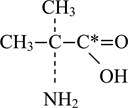
The asterisk (*) indicates the radioactive form of AIB, which is then called α-amino (1-C14) isobutyric acid.
Directionality of AIB transport from maternal to fetal circulations was demonstrated in the dually-perfused human placental lobule [20 , 28]. After 4 hours of perfusion, placental AIB concentration measured at the end of perfusion was 2.3 - 2.8 fold greater than that in maternal or fetal plasma, while the ratio of fetal to maternal plasma was 1.21 [20], the latter having been used as an index of uphill transport across the placenta.
In 1973, Smith et al. reported the first Michaelis-Menten kinetic analysis in human placental villous fragments. A two component uptake pattern was observed over the concentration range 0.1 - 5 mM with a saturable part and a nonsaturable linear component. Incubation of the tissues in amino acid free medium 3 hours prior to kinetic measurements halved the
and trebled
. Miller and Berndt (1974) showed in human placental slices that AIB concentration was saturable over a narrower concentration range of 0.1 - 0.8 mM, when the ouabain-insensitive component was subtracted from the total uptake. Rapid (2 min) AIB uptake in human microvillous membrane vesicles, again with a two component flux pattern, gave comparable kinetic parameters [14]. In the dually perfused guinea pig placenta, the clearance of AIB from maternal to fetal circulation provided saturation kinetics over the range of 0.2 - 1 mM [27]. Eaton et al. (1982) measured kinetics at the fetal, and separately, the maternal interface of the isolated dually perfused guinea pig placenta, using the paired tracer dilution technique. Their results indicate that the
for short chain alanine on the fetal side was similar to that on the maternal side. However, the value for phenylalanine was 3-fold higher than that on the maternal interface, suggesting asymmetry of influx at the two trophoblastic membranes [22].
2.3. Effect of Ethanol
The main intoxicant in alcoholic beverages is ethyl alcohol or ethanol.
Ethanol reaches the blood quickly and is distributed almost uniformly throughout the body [29]. In general, the water solubility of ethanol plays a large part in this uniform distribution. The rapidity of absorption is due to the fact ethanol is absorbed directly into the blood and requires no prior digestion. This rapid absorption is in marked contrast to its slow elimination from the body. The absorption time varies somewhat depending on the conditions under which it is ingested, such as the presence of food in the gastrointestinal tract, the concentration of the ethanol, and the rate at which it is drank. Blood alcohol levels between 500 and 780 mg/dl were recorded in 24 patients in a casualty ward at an incidence of 3 per 1000 patients [30]. The effects from drinking ethanol vary in individuals depending on their tolerance and their history of drinking. Ethanol acts as a depressant primarily on the central nervous system. Since ethanol is lipid soluble, it alters the properties of the cells on the surface layer, thus changing their permeability. This change in permeability is thought to be responsible for an increased resistance, in the surfaces of contact between the different nerve cells. As more ethanol is consumed there is a gradual dissolution of the functions of the central nervous system [31].
The use of ethanol to prevent premature labor served to initiate research on the acute effect of ethanol on the fetus. The maternal and fetal perfusate ethanol concentration time curves were virtually superimposible during the perfusion, and also the placental tissue ethanol concentration measured at the end of perfusion was close to the perfusate concentration [32]. This implies that ethanol is a rapidly diffusible material and freely transferred into the fetal circulation. The fetus depends completely on the placenta and maternal blood for all of the necessities of life, and thus the distribution of ethanol from the mother to the fetus during pregnancy is of special importance. The teratogenic effects of ethanol have been recognized since antiquity, but this knowledge gradually fell into disfavor and was actually dismissed as superstition in the 1940’s [33]. Approximately three decades later, the characteristic pattern of anomalies which came to be known as the fetal alcohol syndrome (FAS) were rediscovered, first in France and then in the United States [34 - 36]. In 1973, Jones et al. described a unique set of characteristics of infants born to women who were chronic alcoholics. These infants exhibited specific anomalies of the eyes, nose, heart, and central nervous system that were accompanied by growth retardation, small head circumference, and mental retardation. The investigators named the condition ‘Fetal Alcohol Syndrome’ (FAS). The effects of ethanol occur not only in the FAS, evident in some offspring of women who are chronic alcoholics, but also in women who have a moderate consumption of ethanol and whose offspring may show reduced birth weight. Behavioral deficits range from mental retardation in children with FAS to less extensive behavioral effects in infants born to women who are social drinkers. Exposure of laboratory animals to ethanol during gestation results in fetal malformations and deaths, growth retardation, and behavioral abnormalities [9].
3. Previous Studies of Modeling
Biomedical engineering illustrates the application of engineering in the service of medicine and biology [37]. Since the body is maintained by a vast number of physical processes and chemical reactions, many chemical engineers have played significant roles as stepping stones between engineering and the life sciences, because of their strong backgrounds in transport phenomena, reaction kinetics, system analysis, mathematics, and model building [16 , 38]. Model building is a powerful tool which uses mathematical language to describe and explain physiological phenomena. When we derive a mathematical model from a complex living system, it is impossible to describe the entire system so precisely that the model behaves exactly like the real system in all respects. Although this perhaps the goal of all people who model physiological systems, a more realistic purpose for modeling is to describe the system by means of mathematics in such a way that the model acts like the real system [39]. A reliable quantitative model based on physiology can serve as a useful framework for designing experiments and evaluating results. Such a model with an appropriated scale up approach based on maximum use of physiological, anatomical, and physicochemical information, may significantly enhance success in the ultimate application in the clinic [40]. Although mathematical modeling can reduce the parameters involved in the physiological phenomena and be used to examine events that cannot be studied experimentally, such an approach should be restricted within a priori knowledge observed experimentally by others, especially if the application of the results from model building is to be used in the clinic.
Compartmental Analysis
In process response analysis, the process and the input are defined and the desired information is the response of the process to the input. Process control problems are examples of this type of operation. Process synthesis problems generally relate to process design, where the process input and output are known and the objective is to find the best route for achieving the desired output. The third type of operation can be termed process input analysis. In this case, the process and the response are known and the process input is desired.
The most common case, especially in biomedical engineering, is the second type. One type of mathematical model used to simulate unknown processes has been the so called “compartment” type. The most common way of applying these models is to try to find the parameters of a sufficient number of compartments in order to fit the experimental data. If the intercompartment transfer is assumed to take place following a linear law, which could be mass flow or diffusion, the balances have the form:
(1)
For constant
, the solution of Equation (1) is known to be a series of exponentials:
(2)
In 1966, Bischoff and Brown studied drug distribution through the circulatory system in mammals. They assumed the tissue was composed of three main types of local regions: capillaries, interstitial fluid, and cells. These were treated as individual compartments and their assembly was used to simulate a larger region. In 1973, Hill and Young studied carbon dioxide transfer in the human placenta using a 4-compartment model for placental vessels: maternal erythrocytes, maternal plasma, fetal plasma, and fetal erythrocytes. In 1974, Reneau et al. developed a lumped parameter model by dividing each fetal organ into two compartments, one for the capillary bed and one for tissue. The placenta was divided into one compartment for the fetal side and another for the maternal side. Volume lumps were placed along the major veins and arteries to account for blood volume and to obtain time delays. Equations were derived using a stirred tank analysis and were solved by means of a digital simulation language CSMP (Continuous System Modeling Program).
In 1974, Hlavinka developed a multi-compartmental patient artificial kidney model to characterize inner body transport during hemodialysis. The blood concentrations of Dextran and Vitamin B-12 were used to determine model parameters, which were searched for by a fourth order Runge-Kutta integration routine until the model best fitted the data. The transcapillary mass transfer coefficients for Dextran and Vitamin B-12 were 502 and 470 ml/min, respectively. Similar approaches were attempted by Popovich et al. (1975). All the compartmental models should be based on physiologically meaningful quantities such as volume, flow rates, system parameters, and not derived by a curve fitting to an arbitrary set of functions. None of the above compartmental approaches were considered “active transport”.
4. Methods and Materials
4.1. Perfusion Technique
Whole placentas with undamaged maternal surfaces and fetal circulations were obtained from the Crouse-lrving Memorial Hospital, which has over 3500 deliveries per year. These normal term placentas from either Caesarian or spontaneous labor delivery were perfused with Krebs-Ringer Bicarbonate (KRB) solution within fifteen minutes after delivery. The umbilical cord was diagonally cut 3 - 4 cm up from the chorionic plate to eliminate the effect of umbilical vessel plasms on fetal flow and to reveal the individual vein and arteries for easy cannulation. Silicone rubber cannulae (8 fr. for arteries and 12 fr. for vein) were inserted up to the anastomosis of the umbilical arteries and tied in place with a cotton string. If the amount of fetal volume loss from the fetal circulation toward the maternal circulation was less than 5 ml/min out of 30 ml/min, it was assumed that the placenta was being adequately perfused. The perfusion apparatus [41] was used to simulate as closely as possible in vivo physical and physiological conditions: fluid pressures, flow patterns, pH, temperatures, and oxygen tensions. The whole apparatus consists of three main parts: the artificial uterus, which holds the placenta with the maternal side downward: the maternal circulatory loop to simulate the maternal circulation: and the fetal circulatory loop to simulate the fetal circulation [8]. KRB solution consisting of NaCl (6.93 g/l), KCl (0.431 g/l), CaCl2 (0.305 g/l), MgSO4・7H2O (0.334 g/l), NaHCO3 (2.106 g/l), glucose (1.63 g/l), heparin (500 unit/l) was used as perfusate. 95 ml of a 6% dextran solution was added to the fetal reservoir to reduce the fetal perfusate transfer. To prevent the occurrence of CaCO3 precipitates from the preparation of KRB, 5-fold concentrated chemical solutions were individually used and the concentrated CaCl2 solution was added drop by drop with mild stirring at the end of mixing. The perfusate was equilibrated before use with individual gas mixtures for the maternal (95% O2 + 5% CO2) and the fetal (5% O2 + 5% CO2 + 90% N2) on the basis of previous studies [42], although in the initial studies of the present work pure CO2 was introduced to both sides whenever necessary to regulate maternal pH and to provide the vasodilator effect of CO2 on the fetal flow rate. The proposed gas mixture provided constant values of pH and pO2 closer to the in vivo conditions. The volume of fetal (820 ~ 920 ml) and maternal (1135 ml) circulations including the dead volumes in the fetal (70 ml) and the maternal (400 ml) loops were monitored by marked scales on the reservoirs. The arterial flow rate in the maternal side was kept at 600 ml/min, while the one in the fetal side at 30 ml/min. The venous flow rate in the fetal side was also monitored to ensure the online observation of the fetal volume loss toward the maternal circulation. All the flow rates were measured by the glass-ball type rotameters (maternal side: Gilmont E1530: fetal side: Gilmont No13) after calibrations with tap water at room condition. After 30 minutes of initial wash out perfusion, the volumes of maternal (735 ml) and fetal (750 - 850 ml) reservoirs were set and required chemicals were added for experimental measurements. Arterial pressures in both sides were monitored by pressure gauges (Marshall town, 0 - 300 mmHg). 1 ml samples of perfusates were drawn from each reservoir every 10 minutes. The pH (Leeds and Northrup 7413) and oxygen tension (Beckman 76) were determined periodically or continuously. At the end of perfusion, the placenta was weighed and 1 gm of tissue samples was collected from three different locations of the well perfused maternal surface for ultrastructural study and radio activity analysis. Our criteria for adequate perfusion were fetal arterial pressures < 110 mmHg and fetal volume loss to the maternal circulation of less than 5 ml/min. Structural integrity can be preserved during perfusion by careful control of the fetal flow rate and the fetal arterial pressure. This integrity was monitored during perfusion by measuring the fetal volume loss, and post perfusion by the observation in light or electron microscopes for edema of the placental ultra structure.
4.2. Measurement Protocol
AIB was added in the nonradioactive form (Sigma Chemical, St. Louis, MO) and as a radioisotope (Amersham, Arlington Heights, IL). (C14-) AIB (57 mCi/mmol) were used with dilution (1 - 5 μCi). The concentrations of perfusate AIB was sequentially changed every one to two hours during experiments of up to 5 hours long. The variables measured during the course of the run were the concentrations of ethanol (~1000 mg/dL) and AIB (5 - 200 mg/l). Tissue concentrations of AIB and ethanol were determined from three tissue samples taken at the end of each run.
In one set of experiments AIB was added to either the maternal or the fetal circulations (single addition technique). In another set of experiments AIB was added simultaneously to both circulations to speed up the formation of the fetal maternal gradient (dual addition technique). The results from the dual addition technique were used to determine not only the net kinetic parameters but also the individual kinetic parameters of Km and Vmax for the uptake from each circulation with and without ethanol. In this way the study could characterize the asymmetry of the transplacental AIB transport mechanism in the absence and presence of ethanol.
4.3. Sample Processing
1 ml perfusate samples mixed with 1 ml 5% trichloroacetic acid (TCA) was centrifuged at 300 rpm for 10 minutes, and 1 ml of each supernatant was placed in a 5 ml plastic vial (Sarstedt, West Germany) with a 4 ml liquid scintillation cocktail (Ready-Solv CP, Bechman). The selection of 5% TCA was based upon the study of Bentler [43]. Placental tissue samples (3) were homogenized using sharp scissors and a glass homogenizer and extracted with 4 ml of 5% TCA, and 1 ml of a supernatant with duplicates that were mixed with a 4 ml cocktail for counting. Radioactivity was counted with a LKB liquid scintillation counter (Rackbeta 1217/1218). Fin-series of alcohols (50% to 100%) and propylene oxide were infiltrated with Araldite 502 medium [44], and then placed in capsules for polymerization in over 50˚C for 18 hours. Thin-sections were prepared with a LKB 2088 ultramicrotome; the grids were double stained with uranyl acetate and lead citrate, and were examined in a Philips EM 300 transmission electron microscope.
5. Theory
5.1. Steady State Models
Steady state measurements have the advantage of simplicity and straight forward interpretation if it is known beforehand that the transport of a substance is flow limited or the flow pattern corresponds to one of the cases considered. Whole placental perfusion steady state measurements require very large volumes of perfusate particularly for the maternal side since the perfusion times are several hours long. The way to overcome this difficulty and the unsteady state model for the transport of diffusion limited substances such as AIB is shown below. In the unsteady state models, the quantity of substances present in the placental tissue can change with time and this change is taken into account by considering a placental tissue as a separate compartment.
5.2. Unsteady State Transport Models
The unsteady state transport models are based upon interpreting the perfusion system and the placenta. The placenta itself is thought of as a series of identical villous capillaries, all of which are perfused in parallel at identical flow rates. The fetal flow rate to these capillaries is less, however, than the fetal flow rate from the fetal reservoir since anatomical evidence and clearance measurements of others [45 , 46] indicate that a fraction of the fetal flow to the umbilical arteries is shunted directly back to the umbilical vein without ever passing through the villous capillary bed.
The maternal perfusate flows over these capillaries. In these experiments, because the maternal perfusate flow rate is much higher than the fetal perfusate flow rate (600 ml/min vs. 30 ml/min), the concentration change of the maternal perfusate in a single pass is much smaller than the fetal change. Consequently, the maternal concentration in the placenta is nearly constant at any time and the flow direction of the maternal perfusate relative to the fetal perfusate is unimportant. Convective transport of the fetal perfusate through channels in the placenta to the maternal perfusate is assumed to account for the transfer of fluid from the fetal to the maternal circulations during perfusion. The several types of placental tissue (syncytiotrophoblast, connective tissues, capillary endothelium) are lumped together into a single composite placenta tissue of volume
with uniform concentration
. This approximation introduces little error for the transfer of flow limited substances since these substances rapidly equilibrate to essentially the same concentration in the maternal perfusate, placental tissue, and fetal perfusate. Because the flow rate of the maternal perfusate is so much higher than the flow rate of the fetal perfusate, the equilibrium concentration becomes essentially equal to the maternal concentration.
For substances whose transport is given by diffusion or other more complicated processes, the lumping approximation is not reasonable. Amino acids such as AIB are actively transported into the trophoblast cell layer and perhaps the capillary endothelium. Exchange across the cell walls also occurs by diffusion. The major resistance to transport across these two placental layers is expected to be in the cell walls, which are lipid in nature, rather than in the cytoplasm of the cells. Thus, three distinct concentrations may be present in the placental tissue; one for the syncytiotrophoblast, one for the connective tissue, and one for the capillary endothelium. Depending on the resistance of the various cell membranes, these concentrations could be nearly the same or distinctly different. Thus, theoretically an arrangement could be made for a more complicated model taking the several tissue layers in account. On the other hand, only one tissue concentration can be measured experimentally i.e., a concentration representing the composite concentration of the tissue. Thus in the interests of simplicity, only one tissue layer was considered here for AIB transport.
5.2.1. Model for AIB Transport
The transport of AIB in the placenta is complex consisting both of an active transport mechanism and a diffusive process. An estimate of whether the fetal flow rate has any significant effect on the rate of transport can be obtained by comparing the time for AIB transport processes into the tissue,
, with the residence time of the fetal perfusate in the capillary bed,
. The effective time for transport into the tissue can be determined (Bassingwaighte and Winkler, 1982) by using an estimate of its effective diffusion coefficient as;
(3)
where L and D are the effective thickness of diffusion barrier and the effective diffusion coefficient, respectively. For a transport barrier thickness of approximately 13 μ accounting for 10 μ of villous membrane thickness [47] and an additional 3 μ of inhomogeneous distribution of fetal capillaries, and a diffusion coefficient of approximately 2 × 10−9 cm2/s,
is about 56 minutes. This is much longer than the residence time (
) of the fetal perfusate in the villous capillaries calculated from
(4)
Consequently, the changes in the fetal perfusate concentration during a single pass is not expected to be large compared to the fetal reservoir concentration and the fetal fluid in the villous capillary will be approximately equal to the concentration in the fetal reservoir. Active transport of amino acids is assumed to take place from both the maternal and the fetal perfusates according to arate expression of the Michaelis-Menten type;
(5)
where
and
are maximum uptake and Michaelis constant of the “k”th compartment. This is equivalent to an enzyme carrier process located in the cell membrane which has a saturable number of sites and whose transport rate from one side of the cell membrane to the other is constant. This type of term is consistent with the expressions used by other investigators for guinea-pig [21 , 22 , 27], rat [48], and human placentas [13 , 14]. In addition, a diffusion process is permitted from both circulations to and from the placenta tissue. Writing the component balances for maternal (
) and fetal (
) circulations and the overall balances for placental tissue (
) compartment gives;
(6)
(7)
(8)
The integral part of the equation from
(the first sample time) to the “n”th samples was used to calculate the placental tissue concentration of AIB (
) from the changes in the concentrations and volumes in the maternal and fetal circulations. For this calculation the sample taken from the maternal and fetal reservoirs and the leak (
) of maternal perfusate from the system was taken into account. Note that no AIB is present in the placental tissue when the first samples from both reservoirs are taken, i.e.,
.
The result is;
(9)
where “Vp” is the uptake of placental tissue. Similarly, the placental uptakes from each circulation are given by;
(10)
(11)
Laga et al. (1973) found that the average wet weight of placenta was 571 gm, while the trimmed volume was 448 cm3, the latter being determined by displacement of water in a 2-liter graduated cylinder [47]. The placental volume (
) used for this study is then assumed to be 78.5% of the individual placental weight. Other techniques available to determine indirectly the placental volume use indicators such as dye, tritiated water, and 3-0-methyl D-glucose, etc. On the other hand, the morphological results from Laga et al. (1973) are direct measurements specifically on the human placenta. Therefore, the placental volume (
) is taken to be equal to a fraction of the wet placental weight (
), the latter being readily measurable;
The uptake at any time is divided by
to determine the placental concentration (
).
Net uptake rates available from the dual addition technique provide the net kinetic parameters with or without ethanol. Individual uptakes from the dual addition technique, however, provide individual kinetic parameters of each circulation as well as% individual uptakes from both the maternal and fetal circulations. That is,
(13)
5.2.2. Pseudo-Steady State Model
In the previous section, it is shown that the placental concentration (
) can be determined experimentally. Let us now formulate an expression for
using the proposed dual active transport model to represent the placental system in terms of measurable quantities and parameters. The placental uptake of AIB is given by;
(14)
where
and
are the constant rates of maternal and fetal active transports corresponding to the constant AIB levels in each circulation.
is the permeability of amino acid in the placenta. The integration of equation gives the simplified form;
(15)
where
(16)
(17)
is expected to be zero for AIB at the beginning of each run.
The placental uptake of AIB as a function of time (t) is then given by;
(18)
values are polynomially regressed with respect to the reciprocal of time until the regression coefficient approaches 1. The intercept of the regressed equation, corresponding to
, gives an approximate value of
.
values are normalized by this approximate value of
and Equation (15) shows that a plot of
vs. time (t), will be a straight line whose slope is then approximately
. These approximate values of
and
serve as initial guesses of
and
for the nonlinear regression of Equation (14). The nonlinear regression package used is GAUSHAUS, whose scheme is based on the combined methods of the least squares and the steepest descent. Parts of its algorithm are similar to those reported by Booth (1949). Thus, the permeability (
) from
and the net active transport rate
from
are determined, respectively. Utilizing these specific parameters, the relative contributions for the Fickian diffusion (
) and the active transport (
) processes upon the net placental uptake (
) of AIB can be determined at any time where;
(19)
Since the net uptake also is the sum of the individual uptakes from the maternal (
) and the fetal (
) circulations, the relative contribution of each process upon each circulation is calculated as;
(20)
where
(21)
(22)
Thus, the individual uptake from maternal (m) or fetal (f) circulations by the processes of diffusion (d) or active transport (a) can be compared with each other.
5.2.3. Numerical Integration
Equations (6) to (8) are solved directly by numerical integration and the values of parameters (
) are varied until the experimental concentrations agree as much as possible with the ones predicted by the integration. The Gear (1971) method which is available from the IMSL routine is used. Its algorithm finds the approximations to the solution of a system of first order ordinary differential equations of the form
with initial conditions. The basic methods used for the solution are of the implicit linear multistep type, which are well described elsewhere [49 , 50].
There are two Equations (6) and (7), with four unknown parameters of
,
,
and
assuming
is known from the pseudo-steady model. The degrees of freedom thus are four. Fitting the experimental data to the equations requires a minimization of the deviations of the predicted values from the experimental data. In order to develop constraints from a simple stability analysis and to provide good initial guesses for the minimization, which involves the numerical integration, the Laplace transform technique is used as follows.
5.2.4. Laplace Transform
Equations (6) to (8) are solved simultaneously by Laplace transform after linearizing Y with a Taylor series expansion in which only the first two terms are kept,
(23)
where
is the initial concentration of “k”th compartment.
(24)
(25)
Thus,
(26)
If
, i.e.
, Equation (26) can be approximated by truncating the second and higher order terms. This inequality is well satisfied in the present experiment. Thus,
(27)
Equation (27) can be simplified as;
(28)
where
(29)
and
(30)
Equations of (29) and (30) indicate that
and
can be calculated once
and
are determined.
Equation (28) is substituted into Equations (6) to (8), and the steady state values can be obtained by setting,
. The result is given by;
(31)
(32)
For the unsteady state, Equation (28) is substituted into equations of (6) to (8) giving;
(33)
(34)
(35)
where
(36)
and
is the steady state value of
.
The above equations can be solved simultaneously by using matrix methods where;
(37)
(38)
(39)
(40)
(41)
(42)
Note that,
(43)
The characteristic equation is then given by;
(44)
where
(45)
and
(46)
Equations (45) and (46) imply that
and
are determined if
and
are specified. Two cases for
and
are possible from Equations (45) and (46):
Case 1:
(47)
(48)
Case 2:
(49)
(50)
where
(51)
(52)
Equations (42) to (44) are combined together to give:
(53)
The final solutions for three Equations (6) to (8), are written as:
(54)
(55)
(56)
All three concentrations are generally expressed by the form:
(57)
where
and
are the functions of unknown parameters:
,
,
,
.
5.2.5. Parameter Estimation
This section attempts to summarize the protocol used for the determination of parameters
.
From Equation (17),
is specified. The permeability of “
” is then given by;
(58)
In order to determine the diffusion coefficient of AIB within the human placenta, we have to know the cross sectional area of the placenta. Laga et al. (1973) reported that the surface area of the maternal side is 15.1 m2 and that of the fetal side 12.0 m2. Since both sides are assumed to have the same permeability (
) and the problem is approached one dimensionally, the arithmetic average of both areas (14.05 × 10 cm4) was used. Note that the surface area is assumed to be proportional to the wet placental weight (
). The units used hereafter are CGS unit, unless specified. The apparent surface area (
) is then given by;
(59)
where 571 is the wet placental weight statistically reported by Laga et al. (1973). Using the definition of permeability and the apparent thickness of placental diffusion barrier (L), the effective diffusion coefficient (D) is expressed as;
(60)
The thickness (L) is assumed to be 13 μ based on the thickness of 10 μ for villous membrane [47] and an additionally possible thickness of 3 μ for the inhomogeneous distribution of fetal capillaries and
is
. Thus, the effective diffusion coefficient (D) is given by combining Equations (59) and (60) as;
(61)
where
is expressed in min−1.
Equation (57) is used to determine the steady state concentration (
) of each circulation by using the nonlinear regression of experimental data. Stability analysis of Equation (44) by Routh criteria provides that;
(62)
From
and
of Equations (45) and (46), respectively, it can be shown;
(63)
In order
to be stable, it is evident from Equation (63) that;
(64)
Thus, if the condition of Equations (5)-(69) is satisfied for any experimental data, the parameters of
can be determined.
Although
and
are defined by Equations (45) and (46), respectively, and their constraints are set forth by Equations (62) and (63), the difference between
and
is not known. Thus,
is redefined as;
(65)
where “h” is a slack variable from 0 to 1 with an arbitrary increment of 0.1.
Note that the indirect parameters of
and
are functions of
and
, respectively if
and
are known, as indicated in Equations (31) and (32).
and
, however, are functions of
and
. as shown in equations from (47) to (52). Therefore, the indirect parameters of
,
,
,
are specified if
and
are known. Unfortunately, the magnitudes of
and
are not known analytically. Instead, the relationship between the two is given by Equation (63). However,
and
are parameters given by the exponential terms of Equation (57). Thus, their values must be somewhere between 0.01 and 0.1 to satisfy the variations of concentration time curves during perfusions of up to 5 hours long. Keeping this fact in mind,
was arbitrarily set and then
is fixed under the constraint f Equation (65). Once approximate values of
and
giving the positive physical parameters of
,
,
, and
(see Equations (29) and (30)) were found,
,
,
,
are assumed to be approximately specified.
Note that such an approach gives the ranges of
and
satisfying the given constraints, rather than providing unique values of
and
. Within the resultant ranges of
and
, the experimental data were fitted for sets of values for
and
until the best fit, given by the Student’s t-test between experimental data and values calculated from the numerical integration, was found. This allowed unique values of
and
to be specified as well as the parameters of
,
,
, and
. The ultimate parameters of
,
,
and
are determined by the relationship derived from Equations (29) and (30) as;
(66)
(67)
(68)
(69)
Such results, along with those from the pseudo steady state model, were used to characterize the mechanism of the amino acid uptake in the human placenta, in the absence and presence of ethanol.
6. Results and Discussion
6.1. Perfusion with and without Ethanol
Results were obtained from thirty term human placentas out of forty-three placentas.
The level of ethanol was fairly constant in three runs for the ethanol study throughout perfusion even though ethanol was being metabolized by the placenta. This was because the ethanol level (500 - 1000 mg/dL) was high enough so that the ethanol metabolized did not substantially decrease the ethanol concentration. No further measurements of ethanol were attempted because the main interest was in its effect on the transport of AIB at a given level of ethanol. The closeness of the maternal and fetal concentrations support previous observations by others indicating that ethanol is a freely diffusible substance.
Twenty six experimental runs out of thirty nine runs with AIB (5 - 100 mg/l) were used to calculate the placental tissue concentration from an overall AIB mass balance. Thirteen runs were completed in the absence of ethanol and thirteen runs in the presence of ethanol (500 and 1000 mg/dL). As summarized in Table 3 & Table 4, the difference of the concentration ratio
of the ethanol group was statistically significant
from the ratio of the control group.
In runs in which AIB was added to both the fetal and maternal perfusates, the fetal AIB concentrations always remained higher than the maternal concentrations. In several runs the calculated placental concentration rose above both the maternal and the fetal perfusate concentrations.
In runs in which AIB was present in both perfusates, the AIB concentrations in each perfusate decreased with time, implying that AIB was being transferred to the placental tissue from both the maternal and the fetal sides. Similar results have been observed by others in the isolated human placental lobule [20]
![]()
Table 3. Experimental conditions of perfusion in the absence of ethanol.
*M → F indicates that AIB is added only to the maternal circulations, while M ↔ F shows that AIB is added simultaneously to both maternal and fetal circulations.
and in the isolated guinea pig placental lobule [21 , 27].
6.2. Diffusion Coefficient of AIB
The calculated placental tissue concentration (
) is used to determine
and
on the basis of Equation (15), the latter being derived from a pseudo steady state model. As shown in Equation (17) or (58), the permeability (
) is calculated from
, which provides the diffusion coefficient of AIB within the human placenta. Seventeen experimental runs were used for this purpose: eight runs in the absence of ethanol and nine runs in the presence of ethanol. The results are represented in Table 5 and Table 6. As shown in Table 5 and Table 6, where several values of the diffusion coefficient were determined even in the same placentas (22, 26 and 35). Such results presumably were caused by the sensitivity of the placental tissue concentration to the value of the first maternal and fetal concentration data points. These values were collected only a few minutes after the addition of AIB to the reservoir, possibly before the perfusate was actually well mixed. The statistical result shows that the diffusion coefficients of AIB in the human placenta are 3.7 × 10−9 cm2/sec and 2.3 × 10−9 cm2/sec for control and ethanol groups, respectively. Their statistical difference is not significant (
).
6.3. Relative Contribution of Each Transport Mechanism
Since
and
were specified in the previous section, the net active transport rate
is derived as;
![]()
Table 4. Experimental conditions of perfusion in the presence of ethanol.
*M → F indicates that AIB is added only to the maternal circulations, while M ↔ F shows that AIB is added simultaneously to both of maternal and fetal circulations. **P value was determined by the Student t-test for unpaired data with equal population variances.
(70)
where
and
are the average concentrations in maternal and fetal circulations, respectively. By Equation (19)
(71)
where
indicates the first derivative of uptake with respect to time and thus represents an uptake rate. From Equation (50),
(72)
From definition,
(73)
Substituting Equations (72) and (73) into (71) gives;
(74)
![]()
Table 5. Diffusion coefficient and active transport rate in the human placental uptake of AIB in the absence of ethanol.
![]()
Table 6. Diffusion coefficient and active transport rate in the human placental uptake of AIB in the presence of ethanol.
Note that
indicates that the net diffusive transport occurs from placental tissue to perfusates, and that
indicates that the transport occurs in the opposite direction.
The relative contribution of diffusive transport,
, to the placental uptake can be given by taking the absolute value of
as
to be free from the direction of transport. Then,
(75)
Thus, the relative contribution of active transport,
, to the placental uptake is given by;
(76)
The results are represented in Table 7 to show that at the beginning of each period diffusion often acts in concert with active transport to transfer AIB to the tissue. As AIB accumulates in the tissue, diffusion acts in a direction opposite to active transport. As the placental tissue approaches its equilibrium concentration, the diffusional contribution becomes equal and opposite to the active transport into the
![]()
Table 7. Relative contributions of diffusive and active transport processes to placental uptake of AIB.
*: Averaged over samples of the run period. **: Averaged over the number of run.
tissue. Table 6 indicates that the relative contribution of active transport on the placental uptake is higher than that of the diffusive transport in both groups; control (52%) and ethanol (65%). Their difference is not a statistically significant (P = 0.70) trend with perfusate AIB concentration.
6.4. Individual Rates and Their Ratios
Thirteen experimental runs were used to determine the individual rates of active transport as well as diffusion from both the maternal and fetal sides, from the results of the relative contribution of transport processes (Table 7), the net rates of active transport.
, are determined. These results are obtained from the pseudo steady state model, in which the perfusate concentrations are assumed to be relatively constant compared to the placental tissue concentration. This approximation is satisfied if the amount taken up by the placental tissue is small compared to the amount present in perfusates. The uptakes of Equation (20) are differentiated with respect to time to give the uptake rates:
(77)
(78)
(79)
where
(80)
(81)
and
represent the maternal and fetal diffusive contributions, respectively, and
and
are assumed constant. Since
and
are relatively constant and
changes markedly,
and
are not constant during the course of a perfusion at a given perfusate AIB concentration. The average values, over the course of the experiment at a given AIB level, were added to the values of
and
to obtain separate values of
and
, respectively. Once
is specified,
is determined from the known value of
, These relationships are based on average rates of active transport, diffusive transport, and net uptake. The ratios of the average values of
and
were also calculated for both the control and the ethanol groups. The calculated
in Table 8 are used to determine the kinetic parameters for the uptake from each side (maternal and fetal uptake). Table 9 summarizes the calculated kinetic parameters. Ethanol seems to inhibit the active transport of AIB from both the maternal and fetal circulations, as indicated by the reduced ratio of
or
in Table 9.
6.5. Numerical Integration
A range of possible values for
and
is first determined using the linearized model. Using this range of each parameter, a direct search is made to obtain the values of
and
which best fit the experimental data to the predictions obtained by the numerical integration of Equations (6) to (8). Values of the parameters obtained by this procedure for eight experimental runs are given in Table 9, which shows a few interesting features. First, the kinetic constant of the maternal side (
) is smaller than that of the fetal side (
), regardless of the presence of ethanol. Second, the maximum velocity constant of the maternal side (
) is larger than that of the fetal side (
), regardless of the presence of ethanol. Thirdly, ethanol administration seems to induce a higher
and a lower
. Finally, the comparison of experimental data with the predicted ones by the GEAR integration technique is satisfactory (P value > 0.60), except for the fetal concentration (P value > 0.4).
6.6. Percent Maternal Uptake and Transfer
Table 10 indicates that the percent of the total AIB uptake which comes from the maternal side in the dual addition experiments is about 65% regardless of the presence of ethanol. This result is consistent with similar ratios of
calculated in the absence and presence of ethanol; 2.6 (control) and 2.5 (ethanol).
![]()
Table 10. Percent maternal uptake and uptake ratio.
*: Averaged over samples of the run period. **: Averaged over the number of runs.
These results imply that the placental uptake from the maternal side governs the net placental uptake of AIB regardless of ethanol presence. Furthermore any reduction in overall AIB uptake by ethanol must be the result of reductions in the uptakes from both the maternal and fetal sides. These results are consistent with those of Van Dijk and Van Krell (1978), who suggested that AIB uptake in the perfused guinea pig placenta takes place from both sides but preferentially from the maternal circulation, and Wier et al. (1982), who reported an abstract suggesting that 70% of the placental AIB originates from the maternal circulation after 4 hours of perfusion using the isolated human placental lobule. The preferential maternal transfer is also observed in the experiments using the single addition technique (Table 9). Although the percent transfer varies with time until a steady state is reached, several interesting features are observed. New paragraph, the total transfer of AIB from the maternal side to the fetal side is higher (49% ± 18%) than the transfer in the opposite direction (21% ± 8%).
In other words, 51% of the amount added to the maternal side is retained by the placental tissue, while 79% of the amount added to the fetal side is retained by the placental tissue. Secondly, the% maternal to fetal transfer (M → F) is probably enhanced by the larger placental tissue uptake from the maternal side. On the other hand, the% fetal to maternal transfer (F → M) is not so large since the uptake rate from the fetal side is smaller. These results support the previous qualitative postulation by Curet (1971) that amino acids, once they leave the maternal circulation, do not immediately cross the placental tissue to be taken up by the fetal circulation. Rather, there is an intermediate stage where amino acids are stored in the placental tissue for a transient period of time, after which they are released into the fetal circulation.
A number of studies have demonstrated that the movement of amino acids across the placenta s bidirectional [20 , 23]. In particular, Wier et al. [20] showed that AIB transfer does occur from the fetus to mother in the guinea pig and human placenta, respectively, at rates slower than in the reverse (M→F) direction. Such results are in good agreement with the present study (Table 10). These results are consistent with those of Yudilevich and Sweiry (1985) who concluded, after their extensive review of the transfer of amino acids including AIB in the placenta, that there is a preferential flux towards the fetal side. This results in a net movement from mother to fetus and explains the generally observed higher amino acid concentrations in the fetal side than in the maternal plasma.
Van Dijk and Van Kreel [27] have reported that increasing the fetal maternal gradient results in an enhanced back diffusion of AIB, which is trapped by the unsaturated carriers and is returned into the fetal circulation. Therefore, it can be concluded from the present study that the placenta tissue plays a role of mediator to maintain a higher fetal concentration than the maternal concentration by either enhancing the % maternal to fetal transfer (M→F) or impairing the% fetal to maternal transfer (F→M).
6.7. Relative Contribution of Transport Process
The relative magnitude of the contribution of active and diffusive processes in the placenta is not apparent from the literature, although Kelman and Sikov (1983) attempted to clarify the relative roles of active and diffusive movements of AIB across the placenta using rapidly diffusible water and actively transported AIB. They proposed that a relatively large component of AIB uptake is of diffusive origin in the in situ placenta. However, their protocol of using tritiated water along with AIB is based on the assumption that the diffusive process of water is equivalent to that of AIB, which is unlikely to be due to the significant difference of their partition coefficients. Thus, the clearance of water may not represent the diffusive process of AIB. However, if AIB is used along with L-glucose instead of water, the diffusive part of AIB can be represented by the transport of L-glucose which has a similar permeability or diffusion coefficient as AIB. L-glucose has been, in fact, used by Yudilevich and his associates [21 , 22 , 51] to eliminate diffusive processes and to determine the kinetic parameters for placental amino acid uptake in the guinea pig using the paired dilution technique. Total AIB uptake is controlled by an active transport mechanism and a diffusive process, the latter being dependent upon the duration of exposure to AIB and the concentration of AIB used [3]. Therefore, the relative contribution can be functions of these factors. The perfusion time consistently indicated in sixteen experimental runs that the diffusive contribution to the net placental uptake of AIB is less than the active contribution for both groups: control (38%) and ethanol (35%). The time curves of each contribution show that the active transport part is higher than the diffusive part during the initial period of perfusion, and that this higher active contribution decreases and the diffusive contribution increases until both are equal to each other at a steady state. Thus, in the experiments reported here it appears that the active transport mechanism governs the placental transport of AIB during the initial transient period of time while both active and diffusive transport have equal rates, but are in opposite directions at a steady state.
6.8. Ratio of the Diffusive Transport Process
As indicated in Table 8, the placental uptake from the maternal circulation is greater than that from the fetal circulation for both active and diffusive processes, regardless of the presence of ethanol. This result is in good agreement with the observation by Dancis et al. [52] showing that only minor amounts of AIB accumulated in the fetal organs during a 2 hour experimental period. Van Dijk and Van Kreel (1978) have shown that the concentration of AIB at the fetal venous outflow exceeds the concentration at the maternal outflow in an open circuit dual perfusion of the guinea pig placenta, which implies that AIB is cleared away from the maternal circulation to a greater extent than its clearance from the fetal circulation. They intended to obtain some idea of the magnitude of diffusional clearance of AIB from mother to fetus and back by making the maternal and fetal ingoing AIB concentrations equal to 2500 mg/l and thus saturating all AIB carriers. Under these circumstances no accumulation in the placental tissue occurred and all AIB going into the placenta was recovered in the fetal side plus the maternal outflow. Their results indicated that AIB diffuses out of the placenta to the fetal and maternal circulation in equal amounts so that the net transport is brought about by the accumulation primarily from the maternal side of the placenta. Such an observation matches the present result of 1.07 ± 0.35 for the diffusive ratio
in the absence of ethanol (Table 11).
In the presence of ethanol, however, the diffusive ratio is increased to 1.43 ± 0.15. Such an altered ratio by ethanol can be due either to increased maternal diffusive transport (
) or to decreased fetal diffusive transport (
). There is a possibility of increased
, since ethanol increases the maternal fluidity, as shown by Wilson and Hoyumpa [53]. However, the results in Table 4 & Table 5 show that the permeability of AIB is decreased by ethanol from 1.4 ml/min/placenta to 15.0 ml/min/placenta. Thus, it appears that ethanol may not only reduce the overall rate of diffusive transport but may also relatively reduce the rate of diffusion to and from the fetal circulation. The ratio of the active transport mechanism from the maternal side (
) to that from the fetal side (
) is increased by ethanol (Table 8). An enhanced ratio may be due to the increased
(Table 11).
![]()
Table 11. Kinetic parameter of individual sides.
R2 indicates the correlation coefficient from the regression of the reciprocal of active rate with respect to the reciprocal of AIB concentration.
The ratios of the active transport to diffusive transport from both the maternal and fetal sides also seem to be increased by ethanol, but the ratio from the fetal side seems to be relatively more, increased. This result in comparison with the above result for
, suggesting that maternal diffusive transport is also reduced by ethanol, but that its extent of inhibition is less than that of the fetal diffusive process. Therefore, the diffusive processes from both circulations may be reduced by ethanol, with the fetal side relatively more inhibited.
7. Conclusions
1) The overall mass balance over the perfusion system can be used to calculate the time course of the placental tissue AIB concentration in the whole human placenta. The latter is consistent with the directly measured tissue concentration at the end of perfusion as long as the duration of perfusion is long enough (>1 hr) and no maternal perfusate is lost toward the outside of the system. The percent error (mean ± standard error) between the calculated and measured placental tissue concentrations is 3% ± 12%.
2) The effective diffusion coefficients of AIB within the human placenta are 3.7 × 10−9 cm2/s (the control group) and 2.3 × 10−9 cm2/s (the ethanol group), with no statistical difference (P = 0.25). The results are comparable to the published data of L-glucose, which has a partition coefficient similar to AIB.
3) The overall placental uptake is higher than that from the fetal circulation, regardless of the presence of ethanol. The ratios of maternal to fetal uptake are 2.6 ± 0.5 for six control runs and 2.5 ± 0.3 for ten ethanol runs, with no statistical difference (P = 0.84).
4) The transfer direction from the maternal to the fetal circulation (49% transferred) is preferred over that from the fetal to the maternal movement (21% transferred). It appears that the placental tissue plays a role of mediator to maintain a higher fetal concentration than the maternal side by either enhancing the maternal to fetal transfer or impairing the fetal to maternal transfer.
5) The relative contribution of the diffusive transport to the net placental uptake of AIB from both the maternal and fetal circulations is less than that of the active transport mechanism for both groups: control (38%) and ethanol (35%) for the dual addition experiments studied here. The results suggest that the active transport mechanism governs the placental uptake of AIB during the initial transient period, while the contributions by active and diffusive processes approach each other at steady state.
6) The placental uptake of AIB from the maternal side by diffusive transport is about the same as the uptake by diffusive transport from the fetal circulation in the absence of ethanol. However, the ratio of the maternal to the fetal diffusive uptakes is much higher (1.43) in the presence of ethanol. The results suggest that diffusive transport on the fetal side is more inhibited by ethanol than is diffusive transport on the maternal side. The result also suggests that the permeability of AIB on the fetal side may be less than that on the maternal side.
7) The placental uptake of AIB from the maternal side by active transport is higher than that from the fetal side for both groups: control (1.3) and ethanol (1.5).
8) The present report appears to be the first wherein individual kinetic analyses for the maternal and fetal AIB active transport in the human placenta have been completed. The results available from the pseudo steady state and the unsteady state approaches, based on the conceptual model of dual active transport, indicate that the active transport mechanisms on both sides are inhibited in the presence of ethanol.
9) An overall effect of ethanol on AIB transport in the perfused human placenta is to significantly (P = 0.016) reduce the ratio of the fetal to maternal perfusate concentrations.
10) In summary, acute in vitro ethanol administration in the perfused whole human placenta reduces both the diffusive and active transport mechanisms of AIB. The extent of inhibition seems to be larger on the fetal side.
Acknowledgements
The authors express sincere appreciations to Dr. Gerald B. Gordon for the ultrastructural study, Dr. Douglas C. Kuhn for constructive suggestion, Dr. Michael S. Baggish and Dr. Robert E. L. Nesbitt for providing facilities of the placental perfusion in the Department of Obstetrics and Gynecology, Upstate Medical Center, State University of New York, USA.