1. Introduction
An Italian Economist and civil engineer, Pareto (1848-1923) introduced the Power law. This law is also known as Pareto Power law and shortly turned into Pareto distribution. Unequal distribution of wealth in society was major cause to establish the Power law. 80% wealth of the population is distributed in 20% population. Thus it is also known as 80 - 20 rule and is stated as N = γx−k where N is the number of individuals with income higher than x for k > 0. Under social constraints of taxation and other conditions this law is proved to be inevitable and universal. Many empirical phenomena are explained by Pareto distribution. Flexibility of Pareto distribution attracted the researchers to develop models by mixing Pareto distribution with other distributions.
Alzaatreh et al. [1] developed Gamma Pareto distribution. Bourguignon et al. [2] introduced the modified form of Pareto distribution presented as “The Kumaraswamy-Pareto distribution”. Nasiru and Luguterah [3] worked on “The New Weibull-Pareto distribution”. Shafiq [4] derived the classical and Bayesian approach on fuzzy observations to draw inference for Pareto distribution and also discussed its characterization and reliability behavior. Exponentiated generalized (EG) class is used by Andrade and Zea [5] to extend the Pareto distribution. Numerous mathematical properties are developed and discussed as well as two real time data sets are modeled by it.
Moment probability distribution or weighted distribution is introduced by Fisher [6] in the context of unequal probability sampling. Mir and Ahmad [7] developed some size biased discrete distributions and also discussed their generalized cases. Dara [8] developed the weighted form of various life time distributions including special cases of size biased distributions with their reliability analysis. Weighted Weibull distribution is size-biased (SWWD) by Perveen and Ahmad [9] . They discussed various characteristic measures and three life data sets are modeled by SWWD.
Exponentiated CDF of a probability distribution is expressed as Exponentiated Distribution (ED). Gompertz [10] used ED to compare the growth model of the population versus table of human mortality. Hasnain and Ahmad [11] proposed and developed the exponentiated moment form of exponential distribution (EME) and discussed its various properties. Fatima and Roohi [12] developed a transmuted form of exponentiated Pareto-I distribution and discussed the increasing and decreasing behavior of hazard rate as well as derived some of its properties. Mansour et al. constructed the Kumaraswamy form of exponentiated Frechet distribution (Kw-EFr) and 27 special cases are developed. Different mathematical properties and real time dataset are modeled by Kw-EFr.
Shaw and Buckley [13] developed Quadratic Rank Transmutation Map (QRTM) to discover new family of non-Gaussian distributions. Let G(x) and g(x) are CDF and PDF of base distribution. Proposed QRTM distribution is
 (1.1)
(1.1)
 (1.2)
(1.2)
where F(x) and f(x) are the CDF and PDF of the corresponding QRTM.
Merovci and Puka [14] proposed the transmuted form of Pareto distribution and discussed various properties along with its reliability behavior. Saboor et al. [15] derived and studied the various structural properties and reliability measures of the transmuted form of exponential-Weibull distribution (TEW). Khan et al. [16] discussed the shape and hazard function of transmuted Kumaraswamy distribution (TK-w) and derived some of its properties. Various properties are discussed in Size-Biased version of Exponential distribution that is transmuted by Hussain et al. [17] .
The authors divided the structure of the article into several sections as follows: Section 2 describes the CDF, PDF and special cases of proposed distribution. In Section 3 and 4, various reliability measures, moments and order statistics are discussed. Quantile function, different descriptive statistics and Rényi entropy are discussed in Section 5. Simulations study is conducted to observe the behavior of MLE estimates in Section 6 while parameters of TEMP distribution are derived by the method of MLE along with two life time data sets are modeled in Section 7. Final conclusion is reported in Section 8.
2. Proposed Distribution
We introduce a four parameter distribution named as Transmuted Exponentiated Moment Pareto distribution (TEMP distribution) with CDF as
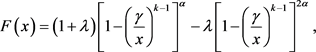 (2.1)
(2.1)
and PDF
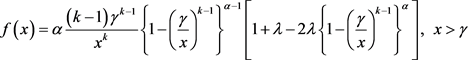 (2.2)
(2.2)
where α and k are positive shape parameters and
is transmuted parameter of TEMP distribution.
Figure 1 is density plot of TEMP distribution. It is plotted for various combinations of parameters α and λ for fixed k.
Cumulative distribution function plot of TEMP distribution at different combinations of parameters α and λ for fixed k are given in Figure 2.
![]()
Figure 1. Probability density function plot of TEMP distribution.
![]()
Figure 2. Cumulative distribution function plot of TEMP distribution.
Some Special Cases
1) For λ = 0, α = 1, and k − 1 = β, the resulting distribution reduces to Pareto distribution.
2) For λ = 0, α = 1, the resulting distribution is Moment Pareto distribution discussed by Dara (8).
3) For k − 1 = β, α = 1, the distribution reduces to Transmuted Pareto distribution and was developed by Merovci and Puka [14] .
TEMP distribution is developed on the basis that it provides more flexible results on highly right skewed datasets. Flexibility of TEMP distribution is assessed by comparing TEMP distribution with Pareto distribution and its related sub model (Transmuted Pareto distribution).
3. Properties of Transmuted Exponentiated Moment Pareto Distribution
3.1. Survival Function of Temp Distribution
Survival or reliability function is used to measure the risk of occurrence of some event at a specific time. It is denoted by S(x).
Survival function S(x) of TEMP distribution is given as
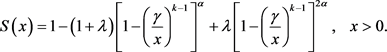 (3.1)
(3.1)
Survival function of TEMP distribution (Figure 3) shows the decreasing behavior on several combinations of parameters α and λ for fixed k.
3.2. Hazard Function of TEMP Distribution
Hazard function was introduced by Barlow et al. [18] . It is time dependent function. It is used to measure the failure rate of some components in a particular period of time x.
For TEMP distribution, hazard function H(x) is given by

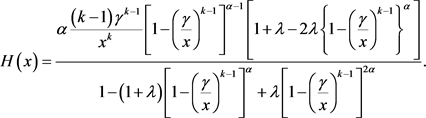 (3.2)
(3.2)
The hazard function of TEMP distribution (Figure 4) for various combinations of parameters for fixed k indicates the increasing trend at initial phase. Longer tail to right shows the decreasing behavior of TEMP distribution.
3.3. Cumulative Hazard Function of TEMP Distribution
Summing up the hazard function from 0 to time (t) is considered as cumulative hazard function. It is denoted by H(t). Only continuous distributions are discussed under it. It is used to measure the overall number of failures that are added up to time t.
Cumulative hazard function is defined as
for TEMP distribution it is described as
(3.3)
The cumulative hazard function of TEMP distribution (Figure 5) indicates
![]()
Figure 3. Survival function plot of TEMP distribution.
![]()
Figure 4. Hazard function plot of TEMP distribution.
![]()
Figure 5. Cumulative hazard function plot of TEMP distribution.
strictly increasing behavior for various combinations of parameters α and λ for fixed k.
3.4. Reverse Hazard Function of TEMP Distribution
From Equation (2.1) and Equation (3.1), reverse hazard rate function of TEMP distribution is
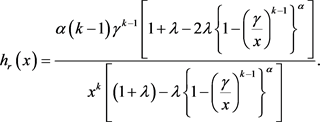 (3.4)
(3.4)
3.5. Mills Ratio of TEMP Distribution
From Equation (2.2) and Equation (3.1), mills ratio of TEMP distribution is
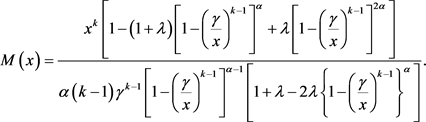 (3.5)
(3.5)
3.6. Odd Function of TEMP Distribution
Symmetric graph of the function w.r.t the origin is said to be odd function.
For TEMP distribution it is defined as
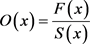
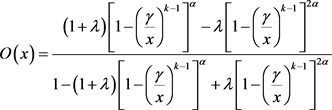 (3.6)
(3.6)
3.7. Elasticity of TEMP Distribution
By definition elasticity is defined as
from Equation (2.1) and Equation (2.2), elasticity of TEMP distribution is written as
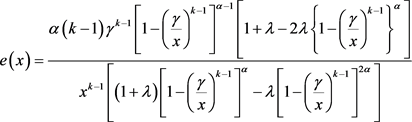 (3.7)
(3.7)
4. Moments
Moments are used to describe the mean, variance, skewness and kurtosis of the probability distribution and it is denoted by m1, m2, m3 and m4 respectively. Different categories of moments including Fractional, factorial, negative, incomplete, L, probability weighted and TL moments are having application in engineering, medicine, natural as well as social sciences.
4.1. Moments about Origin of TEMP Distribution
The r-th moment about origin of TEMP distribution say
is given by
Let
Then
Simplification reduces
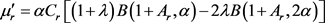 (4.1)
(4.1)
where
,
and
.
4.2. Fractional Positive Moments of TEMP Distribution
Fractional positive moments about the origin of r.v. X following TEMP distribution are given by
![]() (4.2)
(4.2)
where
,
and
.
4.3. Fractional Negative Moments of TEMP Distribution
Fractional negative moments about the origin of r.v. X following TEMP distribution are given by
![]() (4.3)
(4.3)
where
,
and
.
4.4. Negative Moments of TEMP Distribution
rth negative moments about the origin of r.v. X following TEMP distribution are given by
![]() (4.4)
(4.4)
where
,
and
.
4.5. Factorial Moments of TEMP Distribution
Factorial moments of TEMP distribution using Equation (2.2) is given by
![]() (4.5)
(4.5)
where
,
,
,
and
is the Stirling number of first kind.
4.6. Moment Generating Function of TEMP Distribution
Moment generating function (mgf) of r.v. X following TEMP distribution using Equation (4.1) is defined as
![]() (4.6.1)
(4.6.1)
using expansion
, Equation (4.6.1) is written as
using Equation (4.1), mgf of TEMP distribution is
![]() (4.6.2)
(4.6.2)
where
,
,
.
4.7. Central Moments of TEMP Distribution
The central moments of probability distribution are defined by recurrence relation
For TEMP distribution
![]() (4.6)
(4.6)
where
,
and
.
4.8. Cumulants of TEMP Distribution
The cumulants of a probability distribution are defined by the recurrence relation
for TEMP distribution
![]() (4.7)
(4.7)
where
,
and
.
4.9. Skewness of TEMP Distribution
Symmetry of a probability distribution is defined by skewness and it is denoted by
The measure
of TEMP distribution is followed by
![]() (4.8)
(4.8)
where
,
and
.
4.10. Kurtosis of TEMP Distribution
Kurtosis is used to check the spread / peaked of a probability distribution. Kurtosis of a probability distribution is determined by
Kurtosis of TEMP distribution is given by
![]() (4.9)
(4.9)
where
,
and
.
4.11. The Mellin Transformation of TEMP Distribution
In theory of statistics, the Mellin transformation is famous as a distribution of the product as well as quotient for independent r.v.’s. By definition the Mellin transformation is
for TEMP distribution, from Equation (4.1)
![]() (4.10)
(4.10)
where
,
and
.
4.12. Incomplete Moments of TEMP Distribution
For TEMP distribution, lower incomplete moments are defined as
From Equation (4.1), ![]() , replace Beta function by
, we get
, replace Beta function by
, we get
![]() (4.11.1)
(4.11.1)
where
,
and
.
For TEMP distribution, upper incomplete moments are defined as
from Equation (4.1), replace Beta function by
, we get
![]() (4.11.2)
(4.11.2)
where
,
and
.
4.13. Residual Life Function of TEMP Distribution
Let residual life
of X for TEMP distribution has n-th moment.
(4.12)
For life expectancy or mean residual life (MRL) function say
of TEMP distribution put n = 1 in Equation (4.12), we get
![]() (4.12.1)
(4.12.1)
where
,
and
.
4.14. Reverse Residual Life Function of TEMP Distribution
Let reverse residual life
of X for TEMP distribution has n-th moment.
![]() (4.13)
(4.13)
For mean waiting time or mean inactivity time of TEMP distribution put n = 1 in Equation (4.13), we get
![]() (4.13.1)
(4.13.1)
where
,
and
.
4.15. Order Statistic of TEMP Distribution
Reliability of a system is tested by order statistic. The random sample provides important information like smallest value to largest value. To maintain the highest temperature of a medicine or lowest temperature of areas are the examples studied by order statistic to overcome the crisis or disasters in case of emergency.
Let
be a random sample follows to TEMP distribution and ![]() be its arranged form where X(1) and X(k) represent the smallest and k-th smallest value follows to
respectively. The r.v.s
are called order statistic.
be its arranged form where X(1) and X(k) represent the smallest and k-th smallest value follows to
respectively. The r.v.s
are called order statistic.
Order statistic for pdf of X(i) is defined as
for TEMP distribution, order statistic for pdf of X(i) is
order statistic of TEMP distribution in reduced form
![]() (4.15)
(4.15)
for TEMP distribution, largest order or m-th order statistic pdf X(m) is given by
![]() (4.15.1)
(4.15.1)
and first order or smallest order statistic pdf X(1) for TEMP distribution, is given by
![]() (4.15.2)
(4.15.2)
From Equation (4.15), r-th moment of order statistic for TEMP distribution in simplified and reduced form is given by
![]() (4.16)
(4.16)
where
5. Quantile Function and Descriptive Statistics of TEMP Distribution
Statistical significance is assessed by the quantile function of the observations for known distribution. It is defined by inverting the CDF under consideration. When information about the data set is quantitatively reviewed or analyzed by the summary statistics, it is called descriptive statistics.
5.1. Quantile Function of TEMP Distribution
The qth quantile function of TEMP distribution is
![]() (5.1)
(5.1)
Median of a distribution is
for q = 0.5. For TEMP distribution we put q = 0.5 in Equation (5.1), we get
![]() (5.2)
(5.2)
To generate random numbers, we suppose that CDF of TEMP distribution follows uniform distribution u = U (0, 1).
Random numbers of TEMP distribution is calculated by
![]() (5.3)
(5.3)
Coefficient of variation is defined as the quotient of standard deviation (SD) to mean.
Coefficient of variation of TEMP distribution is
![]() (5.4)
(5.4)
where
,
and
.
From Equation (3.4.1) set
, we get harmonic mean of TEMP distribution
(5.5)
5.2. Entropy of TEMP Distribution
Degree of disorder or randomness in a system or our lack of information about it is defined as Entropy. In information theory, the Rényi entropy generalized Hartley entropy, Shannon entropy, Collision and min entropy. Entropies quantify the diversity, uncertainty or randomness of a system.
Rényi [19] entropy is defined as
From Equation (2.2), the reduced form of Rényi entropy of TEMP distribution is given by
(5.7)
where
,
,
,
and
.
5.3. Mixture Representation of TEMP Distribution (Figure 6)
The PDF of “n” mixture of TEMP distribution is followed by
, where
and
for TEMP distribution from Equation (2.2) is
![]() Mixture Density Plot of TEMP distribution for n = 2 at various combination of parameters
and
for fixed value of
Mixture Density Plot of TEMP distribution for n = 2 at various combination of parameters
and
for fixed value of
Figure 6. Mixture density plot TEMP distribution.
defined as
For n = 2, mixture form of TEMP distribution is given by
For n = 3, mixture form of TEMP distribution is given by
(5.8)
From Equation (4.1), r-th moment of mixture form of TEMP distribution is written as
(5.9)
where
,
and
.
6. Simulation Study of TEMP Distribution
In order to assess the behavior of estimates derived by the method of MLE from TEMP distribution, a small scaled experiment is carried out based on simulations study. Performance of MLE is evaluated on the basis of mean square errors (MSEs). For this we generate size n = 100, 200, 300, 400 and 500 samples from Equation (5.3) and results are achieved by 1000 simulations. Statistical software R is used to develop the empirical results.
Table 1 and Table 2 are representing consistent and efficient performance of the estimates produced by MLE and these estimates are quite close to the true parameter values for entire n. The decreasing behavior of mean square errors justify that the MLE works quite well for TEMP distribution (Table 3, Table 4).
7. Estimation of Parameters and Application of TEMP Distribution
Parameters of Transmuted Exponentiated Moment Pareto distribution are calculated using the method of MLE by incorporating R package (statistical software).
7.1. Estimation of Parameters of TEMP Distribution
Log likelihood function of TEMP distribution under Equation (2.2) is stated as
![]()
Table 1. MLE Estimates and Mean Square Errors (MSEs) in parenthesis are calculated at various sample sizes for k = 1.5, α = 0.5 and λ = −0.4 and parameter γ is minimum possible value of x.
![]()
Table 2. MLE Estimates and Mean Square Errors (MSEs) in parenthesis are calculated at various sample sizes for k = 2.5, α = 1.5 and λ = 0.1 and parameter γ is minimum possible value of x.
![]()
Table 3. Various results of Descriptive measures on simulated data generated by the Equation (5.3) at different samples sizes n = 25, 100, 200, 300, 400 and 500 for selected values of k = 1.5, α = 0.5 and λ = −0.4.
![]()
Table 4. Various results of descriptive measures on simulated data generated by the Equation (5.3) at different samples sizes n = 25, 100, 200, 300, 400 and 500 for selected values of for k = 2.5, α = 1.5 and λ = 0.1.
(7.1.1)
Partial derivatives of Equation (7.1.1) w.r.t the parameters k, α and λ are calculated and equating to zero we get.
(7.1.2)
(7.1.3)
(7.1.4)
Since γ is the initial point of PDF, as a minimum possible value of sample is the estimate of γ. Solution of simultaneous Equations (7.1.2)-(7.1.4) gives us MLE estimates of TEMP distribution. We solve these non linear equations by using R package.
Fisher Information matrix
of order 3 × 3 is required for hypothesis test and interval estimation.
is described as
(7.1.5)
7.2. Application of TEMP Distribution
To show that Transmuted Exponentiated Moment Pareto (TEMP) distribution is better than its sub-models Transmuted Pareto (TP) and Pareto (P) distributions, authors consider four data sets. In R, package Adequacy Model and method BFGS is used to derive the estimates.
7.2.1. Dataset-1
Choulakian and Stephens [20] discussed the dataset entitled with the exceedances of flood peaks (in m3/s) of the Wheaton River in Canada. This data set is also discussed by Merovci and Puka [14] (Table 5).
7.2.2. Dataset-2
Remission times (in months) of bladder cancer 128 patients sample is discussed by Lee and Wang [21] (Table 6).
7.2.3. Dataset-3
Barlow et al. [22] developed the dataset corresponding to the Kevlar 49/epoxy strands failure times (pressure at 90% age) (Table 7).
7.2.4. Dataset-4
Ghitany et al. [23] discussed the waiting time (in minutes) before the customer
![]()
Table 5. Parameter estimates and information criterion. (Since γ is the initial point of PDF, as a minimum possible value of sample is the estimate of γ = 0.1.)
![]()
Table 6. Parameter estimates and information criterion. (Since γ is the initial point of PDF, as a minimum possible value of the sample is the estimate of γ = 0.08.)
![]()
Table 7. Parameter estimates and information criterion. (Since γ is the initial point of PDF, as a minimum possible value of the sample is the estimate of γ = 0.01.)
![]()
Table 8. Parameter estimates and information criterion. (Since γ is the initial point of PDF, as a minimum possible value of the sample is the estimate of γ = 0.8.)
receives service in a bank on 100 observations (Table 8 and Figure 7).
8. Conclusions
In this article, authors have developed a new four parameter model named Transmuted Exponentiated Moment Pareto (TEMP) distribution. Numerous mathematical properties of TEMP distribution are discussed. TEMP distribution is modeled by four suitable lifetime data sets. Authors calculate the values of -LL and information criterion (AIC, BIC, A, W, K-S) on data set 1 to 4. TEMP
![]()
Figure 7. PDF plots drafted over empirical histogram.
distribution is compared with its sub-models. Based on the minimum value of -LL and information criterion it is concluded that TEMP distribution is most favorable fit distribution as compared to its sub-models Transmuted Pareto (TP) and Pareto distribution.
In future numerous properties of Bayesian analysis of TEMP distribution will be studied.