1. Introduction
Many physicists have emphasized the unreasonable effectiveness of mathematics in describing the physical world; among them the most authoritative one is Wigner [1] . An anecdote clarifies Wigner’s perplexity. Two students were discussing the ability of describing the statistical distribution of hungers in the world through the Gauss function, which involves the number . Strictly speaking, it is hard to realize what has to do the geometrical ratio between circumference and radius of a circle with the distribution of hungers; even in lack of a rational explanation, though, nobody could doubt about the ability of scientists to contribute to the advancement of science introducing
. Strictly speaking, it is hard to realize what has to do the geometrical ratio between circumference and radius of a circle with the distribution of hungers; even in lack of a rational explanation, though, nobody could doubt about the ability of scientists to contribute to the advancement of science introducing 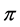 in the frame of sophisticated mathematical algorithms.
in the frame of sophisticated mathematical algorithms.
Even Bertrand Russel was concerned about the link between mathematics and physics [2] . In his book “Study of Mathematics” he says: “Mathematics, rightly viewed, possesses not only truth, but supreme beauty, a beauty cold and austere like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as in poetry.”
Nevertheless, the outcomes of the natural sciences are subjected to experimental tests: what is false or true is definable regardless of hungers and geometrical distresses. On the one hand, abstract numbers express reliable physical laws describing properties and predicting behavior of Nature. On the other hand, however, this epistemological shortcut in fact leaves unexplained the link between science and reality, calculation and experiment, mental ideas and actual story of the Universe. Quoting Einstein “the most incomprehensible thing of the Universe is that it is comprehensible”.
Paradoxically, it is easy to understand the correlation between mathematical algorithm and natural event assuming first deterministic evolution of systems according to the old classical physics: once having selected properly the initial conditions, the successive evolution is in principle uniquely determinable. In practice any deterministic model requires a suitable number of descriptive parameters exactly known of a whole system, whose time evolution is codified and described via appropriate functions of these parameters; the mathematical definitions valid at a given time , remain also valid, if correctly chosen, at
, remain also valid, if correctly chosen, at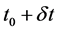 . Extrapolating this reasoning, the outcomes of such a model hold at any times
. Extrapolating this reasoning, the outcomes of such a model hold at any times 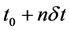 even for
even for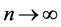 : everything exactly known at
: everything exactly known at 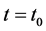 remains exactly knowable forever. This should be true in principle also for a classical Universe, regarded as a whole physical system.
remains exactly knowable forever. This should be true in principle also for a classical Universe, regarded as a whole physical system.
Actually however the problem is much more complicated.
The task of guessing the evolution of a physical system from a given initial condition must settle up with the probabilistic frame of the quantum theory: uncertainty relationships imply the impossibility of knowing simultaneously couples of conjugate dynamical variables. This constrain at the time 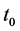 prevents the possibility of their exact knowledge at any later time as well. Worse still, an initial energy uncertainty
prevents the possibility of their exact knowledge at any later time as well. Worse still, an initial energy uncertainty 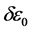 compels a subsequent range
compels a subsequent range 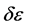 of possible values that depends itself upon the choice of
of possible values that depends itself upon the choice of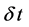 . As a matter of fact, however, the fundamental laws of quantum physics are successful in conceiving correctly and designing operatively transistors and lasers.
. As a matter of fact, however, the fundamental laws of quantum physics are successful in conceiving correctly and designing operatively transistors and lasers.
The predictive ability of science becomes further at stake considering also the relativistic theory, according which 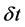 and
and 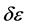 have meaning only relatively to the particular reference system where they are initially defined: e.g. the twin paradox exemplifies that the time is not an absolute parameter, as the reciprocal motion of their reference systems R and
have meaning only relatively to the particular reference system where they are initially defined: e.g. the twin paradox exemplifies that the time is not an absolute parameter, as the reciprocal motion of their reference systems R and 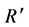 implies anyway admitting different time lapses
implies anyway admitting different time lapses  and
and 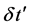 for a given event to occur and even for their aging. The necessity of specifying both reference systems to describe physical events explains why the physical laws must be formulated in a covariant way.
for a given event to occur and even for their aging. The necessity of specifying both reference systems to describe physical events explains why the physical laws must be formulated in a covariant way.
Moreover the link between quantum and relativistic theory is still a hard challenge even today.
To approach gradually the epistemological problem raised by these short considerations, suppose preliminarily that a given event K is allowed to occur in a given R at the arbitrary time , waiving for the moment whether or not actually this time is exactly determinable; in this R are also defined the initial time
, waiving for the moment whether or not actually this time is exactly determinable; in this R are also defined the initial time ![]() and the pertinent boundary conditions. Let K be for example the motion of a classical system of N particles, described by a total number J of descriptive parameters
and the pertinent boundary conditions. Let K be for example the motion of a classical system of N particles, described by a total number J of descriptive parameters![]() : e.g. position coordinates
: e.g. position coordinates![]() , momentum components
, momentum components![]() , energies
, energies ![]() and so on of each i-th particle with
and so on of each i-th particle with![]() . Of course
. Of course ![]() can include also mutual interactions, presence of external fields and anything else. Shortly,
can include also mutual interactions, presence of external fields and anything else. Shortly, ![]() symbolize in general the j-th dynamical variables significant to define the state of each particle at the time
symbolize in general the j-th dynamical variables significant to define the state of each particle at the time![]() , in principle all measurable. Moreover let be known also the experimental value of the observable
, in principle all measurable. Moreover let be known also the experimental value of the observable ![]() of a given property V characterizing the event K at the time
of a given property V characterizing the event K at the time ![]() and reproduce this value as a linear combination
and reproduce this value as a linear combination ![]() of its descriptive parameters via appropriate coefficients
of its descriptive parameters via appropriate coefficients![]() . A simple example clarifies this point. Consider a one dimensional system of two interacting particles having initial coordinates
. A simple example clarifies this point. Consider a one dimensional system of two interacting particles having initial coordinates ![]() and
and ![]() at the time
at the time![]() ; concerning first the initial boundary condition, write
; concerning first the initial boundary condition, write
![]()
being all dynamical variables known by definition, regard the coefficients ![]() as parameters that fit the initial value
as parameters that fit the initial value ![]() of total energy of the system; also, are experimentally measured the space and time coordinates and the energies
of total energy of the system; also, are experimentally measured the space and time coordinates and the energies ![]() and
and![]() , upon which depends the interaction energy
, upon which depends the interaction energy ![]() assumed known as well. Repeat this reasoning, but considering now the total energy
assumed known as well. Repeat this reasoning, but considering now the total energy ![]() of the system at the arbitrary time
of the system at the arbitrary time![]() ; it is in principle possible that the same equation links
; it is in principle possible that the same equation links ![]() to the new space and time coordinates
to the new space and time coordinates ![]() and
and![]() , energies
, energies ![]() and
and![]() , and interaction energy
, and interaction energy![]() . Assuming experimentally known all these quantities, the new linear combination involving the same dynamical variables reasonably determining
. Assuming experimentally known all these quantities, the new linear combination involving the same dynamical variables reasonably determining ![]() experimentally known as well reads
experimentally known as well reads
![]()
In principle it is possible that the coefficients![]() , with
, with ![]() in this example, fit not only the initial boundary condition but also this further equation. In practice, however, neither the former equation nor the latter are calculable because two equations do not define uniquely the six unknowns
in this example, fit not only the initial boundary condition but also this further equation. In practice, however, neither the former equation nor the latter are calculable because two equations do not define uniquely the six unknowns![]() ; the system of equations is actually undetermined. But it is possible to measure all dynamical variables also at the subsequent arbitrary times
; the system of equations is actually undetermined. But it is possible to measure all dynamical variables also at the subsequent arbitrary times ![]() or
or ![]() and so on, which yields
and so on, which yields
![]()
It is clear that further sets of six experimental data obtained measuring the same quantities at five additional times with respect to the initial condition, yield a system of six equations with six unknowns. Now the system admits a unique solution for all ![]() fulfilling by definition also the boundary condition. In principle this empirical procedure is possible no matter how complex is the system and how many its freedom degrees might be; a suitable number J of experimental measurements allow to obtain coefficients
fulfilling by definition also the boundary condition. In principle this empirical procedure is possible no matter how complex is the system and how many its freedom degrees might be; a suitable number J of experimental measurements allow to obtain coefficients ![]() that fit by definition all values of the observable
that fit by definition all values of the observable ![]() of interest at any time between
of interest at any time between ![]() and
and![]() . The various
. The various ![]() are therefore not only the respective
are therefore not only the respective ![]() but also any other dynamical variable that concur with all
but also any other dynamical variable that concur with all ![]() and
and ![]() to the resulting value of the observable
to the resulting value of the observable![]() ; it is clear why one of the dynamical variables must be just the pertinent time
; it is clear why one of the dynamical variables must be just the pertinent time![]() . Note that, owing to the empirical character of the linear combination, even the higher powers of some descriptive parameters, e.g.
. Note that, owing to the empirical character of the linear combination, even the higher powers of some descriptive parameters, e.g. ![]() are in principle admissible with their own
are in principle admissible with their own ![]() among the terms contributing to
among the terms contributing to![]() .
.
Anyway take for granted that, by definition, all coefficients ![]() fit correctly the known values of the experimental parameters
fit correctly the known values of the experimental parameters ![]() of all particles concurring to the required value
of all particles concurring to the required value![]() .
.
On the one hand, is comprehensible the interest to describe the system at subsequent times after that of the initial condition for completeness of information. On the other hand, however, since in general the descriptive parameters are functions of time, e.g. the dynamical variables of the various particles, the evolution of the system during a given time range becomes in fact essential requirement for the mathematical approach: repeating the same numerical procedure at ![]() subsequent times
subsequent times ![]() after the initial
after the initial![]() , one can define a set of J equations and thus a square matrix of coefficients
, one can define a set of J equations and thus a square matrix of coefficients ![]() whose lines fit exactly by definition the experimental values
whose lines fit exactly by definition the experimental values ![]() of the observable V in the given time range. Write therefore
of the observable V in the given time range. Write therefore
![]() (1.1)
(1.1)
the system of equations removes the indeterminacy inherent a unique observation time and contextually describes how a given observable of the system changes at various times![]() , although without rational or heuristic valence. Nonetheless the following evolution matrix represents the minimal condition able to characterize mathematically one property V of one event K of the system, although waiving any chance of physical explanation:
, although without rational or heuristic valence. Nonetheless the following evolution matrix represents the minimal condition able to characterize mathematically one property V of one event K of the system, although waiving any chance of physical explanation:
![]() (1.2)
(1.2)
Every column of the matrix ![]() represents the values of each descriptive parameter governing V at various times, every line concerns the values of all possible descriptive parameters contributing to the value
represents the values of each descriptive parameter governing V at various times, every line concerns the values of all possible descriptive parameters contributing to the value ![]() at the particular time
at the particular time ![]() regardless of explaining how it was at the past
regardless of explaining how it was at the past ![]() or will be at the future
or will be at the future![]() . The matrix elements defined by a set of successive measurements fit therefore “a posteriori” the evolution of the observable V, i.e. simply reproducing mathematically what is experimentally known in the considered time range. This empirical procedure, in principle non-predictive, is to be repeated at all times and extended to each observable of any event K of interest to characterize the whole system.
. The matrix elements defined by a set of successive measurements fit therefore “a posteriori” the evolution of the observable V, i.e. simply reproducing mathematically what is experimentally known in the considered time range. This empirical procedure, in principle non-predictive, is to be repeated at all times and extended to each observable of any event K of interest to characterize the whole system.
Moreover ![]() implies neither past nor future: exchanging two lines, the change of sign of
implies neither past nor future: exchanging two lines, the change of sign of ![]() is canceled by that of
is canceled by that of ![]() concurrently necessary, i.e.
concurrently necessary, i.e. ![]() remains unchanged.
remains unchanged.
On the one hand this procedure, seemingly sterile, deserves attention as it shows that the link between numerical representation of the reality and physical events is in fact plausible: mathematics has its own rules to elaborate numbers; if these rules are implemented to reproduce the results of measurements, then the efforts of scientists are addressed to convert this empirical analysis of data, correct by definition, into rational information to be understood. So Wigner’s doubts are bypassed regarding in fact the empiricism as an intermediate step between mere observation and profound knowledge of the reality, which however remains implicitly hidden in the raw data.
On the other hand all previous considerations evidence three key requirements necessary for any theoretical attempt to bridge abstract numbers and informative interpretation of results: 1) it must be holistic, 2) it must have space time structure, 3) it must inherently have evolutionary character. These three points prospect the non-trivial heuristic worth of![]() : despite its pragmatic character, the coefficients of each line of the matrix and thus the matrix itself fulfill by definition these requirements and have thus physical valence. Also,
: despite its pragmatic character, the coefficients of each line of the matrix and thus the matrix itself fulfill by definition these requirements and have thus physical valence. Also, ![]() demonstrates the inherent rationality of Nature, without which no best fit technique could provide sensible outcomes. By consequence, no conceptual doubt exists about the effectiveness of a rational approach in describing mathematically the reality.
demonstrates the inherent rationality of Nature, without which no best fit technique could provide sensible outcomes. By consequence, no conceptual doubt exists about the effectiveness of a rational approach in describing mathematically the reality.
In principle is difficult to discern, on the basis of a linear combination of parameters only, whether for example two arbitrary time ranges ![]() and
and ![]() differ because they refer to different reference systems in reciprocal motion or because of the presence of a gravity field or even because the quantum uncertainty implies corresponding energy ranges
differ because they refer to different reference systems in reciprocal motion or because of the presence of a gravity field or even because the quantum uncertainty implies corresponding energy ranges ![]() and
and![]() . Is evident thud the necessity of overcoming the mere empiricism hitherto preliminarily proposed, while acknowledging that the predictive ability of any theory is nothing else but its ability to reproduce the values of the aforesaid coefficients via rational path as general as possible, i.e. starting from first principles. In particular, it appears also necessary to identify rationally one by one the parameters
. Is evident thud the necessity of overcoming the mere empiricism hitherto preliminarily proposed, while acknowledging that the predictive ability of any theory is nothing else but its ability to reproduce the values of the aforesaid coefficients via rational path as general as possible, i.e. starting from first principles. In particular, it appears also necessary to identify rationally one by one the parameters ![]() in fact concurring to describe exhaustively any physical event K.
in fact concurring to describe exhaustively any physical event K.
The idea is at this point to bypass the best fit approach, valid by definition, by introducing a general function
![]() (1.3)
(1.3)
the index r stands for the set of three space coordinates and related vector components of all dynamical variables characterizing the system, e.g. possible internal and external vector fields ![]() suitable to affect the evolution of all its constituting particles, the dots indicate any further j-th descriptive parameter additional to
suitable to affect the evolution of all its constituting particles, the dots indicate any further j-th descriptive parameter additional to ![]() and
and ![]() possibly necessary. The last three positions allow writing implicitly and simply
possibly necessary. The last three positions allow writing implicitly and simply ![]() via the various
via the various ![]() of all j-th descriptive parameters contributing to the k-th line of
of all j-th descriptive parameters contributing to the k-th line of ![]() at the time
at the time![]() . For example
. For example ![]() is itself a shortcut of
is itself a shortcut of![]() ; indeed
; indeed ![]() at various
at various ![]() are somehow determined themselves by the strengths of the fields possibly acting on the system. So the Equation (1.3) can be shortened without loss of generality writing
are somehow determined themselves by the strengths of the fields possibly acting on the system. So the Equation (1.3) can be shortened without loss of generality writing ![]() as
as
![]() (1.4)
(1.4)
having nested into X all possible descriptive parameters implicitly governing the physical state of the system.
It is clear that the strategy of implementing the form (1.4) as a starting point, requires to extract successively from ![]() information about the possible external fields concurring to the internal interactions in defining
information about the possible external fields concurring to the internal interactions in defining ![]() previously quoted. But how could the primordial function
previously quoted. But how could the primordial function ![]() summarize the variety of phenomena symbolized by every possible observable
summarize the variety of phenomena symbolized by every possible observable ![]() for all possible physical events K?
for all possible physical events K?
Try to simplify the problem: although in principle the following considerations hold even for![]() , as postulated in some physical theories [3] , assume for simplicity and without conceptual limitation a two dimensional space time, with the time coordinate and one space coordinate only. In this assumed one dimensional space
, as postulated in some physical theories [3] , assume for simplicity and without conceptual limitation a two dimensional space time, with the time coordinate and one space coordinate only. In this assumed one dimensional space ![]() can be omitted, whereas the space coordinates and respective vector components are represented by the unique index j that now refers to the various particles of the system. Accordingly, it is eventually possible to write more shortly
can be omitted, whereas the space coordinates and respective vector components are represented by the unique index j that now refers to the various particles of the system. Accordingly, it is eventually possible to write more shortly ![]() intending now j extended to the freedom degrees of all particles of a given physical system at the time
intending now j extended to the freedom degrees of all particles of a given physical system at the time![]() . So any physical effect determining the behavior of the system is described via one dimensional approach with two space time coordinates only for each freedom degree; this bypasses the difficulty of guessing one by one the descriptive parameters that effectively govern case by case the event K. Compare now the early empirical expression (1.1) with the series expansion of
. So any physical effect determining the behavior of the system is described via one dimensional approach with two space time coordinates only for each freedom degree; this bypasses the difficulty of guessing one by one the descriptive parameters that effectively govern case by case the event K. Compare now the early empirical expression (1.1) with the series expansion of ![]() around arbitrary initial coordinates
around arbitrary initial coordinates ![]() and
and![]() , which reads
, which reads
![]() (1.5)
(1.5)
the summation over i accounts for the arbitrary number I of terms of the series, that on j reproduces the same number of terms of the linear combination (1.1), the index ![]() still represents the time at which the descriptive parameters j are expressed when defining the time change of an appropriate function
still represents the time at which the descriptive parameters j are expressed when defining the time change of an appropriate function ![]() of all the necessary parameters. The notation indicates that the derivatives of
of all the necessary parameters. The notation indicates that the derivatives of ![]() are calculated at arbitrary
are calculated at arbitrary ![]() and
and ![]() defining
defining ![]() in a given R, e.g. the laboratory. So each term j of (1.1) takes the form
in a given R, e.g. the laboratory. So each term j of (1.1) takes the form
![]() (1.6)
(1.6)
the additive term is assumed known, being the initial boundary condition of the problem. Each j-th term is still related to the respective parameter ![]() of the best fit procedure at the time
of the best fit procedure at the time![]() , although with a small difference. Previously
, although with a small difference. Previously ![]() were selected quantities implied by the physical event K (all measurable dynamical variables, among which
were selected quantities implied by the physical event K (all measurable dynamical variables, among which ![]() and
and![]() ) tentatively introduced one by one; the best fit procedure aimed to calculate the respective coefficients
) tentatively introduced one by one; the best fit procedure aimed to calculate the respective coefficients ![]() reproducing the known values of
reproducing the known values of ![]() (the specific physical property of interest) at the time
(the specific physical property of interest) at the time![]() . Here instead the series expansion yields numerical coefficients
. Here instead the series expansion yields numerical coefficients ![]() given by derivatives of a unique unknown function
given by derivatives of a unique unknown function ![]() calculated once for all at prefixed space and time coordinates initially set. The descriptive parameters are
calculated once for all at prefixed space and time coordinates initially set. The descriptive parameters are![]() , i.e. combinatorial factors times various products of space time ranges
, i.e. combinatorial factors times various products of space time ranges ![]() and
and![]() : the dynamical variables previously tentatively introduced via the respective descriptive parameters
: the dynamical variables previously tentatively introduced via the respective descriptive parameters ![]() correspond now to the space coordinates of all particles that still represent space and time experimental inputs. If these latter are known, then (1.6) and (1.1) are equivalent as concerns the best fit approach, defined again by a linear system of equations with best fit unknowns
correspond now to the space coordinates of all particles that still represent space and time experimental inputs. If these latter are known, then (1.6) and (1.1) are equivalent as concerns the best fit approach, defined again by a linear system of equations with best fit unknowns![]() . Yet, as by definition the coordinates depend upon all fields possibly acting on the system, summarized by
. Yet, as by definition the coordinates depend upon all fields possibly acting on the system, summarized by ![]() at given
at given ![]() and nested like in (1.4) and (1.3), further calculations are necessary to go back from these coordinates experimentally measured to the strength of the fields hidden in
and nested like in (1.4) and (1.3), further calculations are necessary to go back from these coordinates experimentally measured to the strength of the fields hidden in![]() . Nonetheless there is more information in (1.6) than in (1.1): the correlation of the actual experimental data to the initial conditions is not simply reasonable, it is required by the concept of space time ranges themselves.
. Nonetheless there is more information in (1.6) than in (1.1): the correlation of the actual experimental data to the initial conditions is not simply reasonable, it is required by the concept of space time ranges themselves.
The next step to overcome the legitimate Wigner doubts is just the time correlation (1.5), which does exist indeed and involves space time ranges as they appear in (1.6), not the local ![]() and
and![]() .
.
The worth of this information appears just from these equations comparing the particular cases where ![]() and
and ![]() in (1.6). Since in the former case
in (1.6). Since in the former case![]() , the summation on
, the summation on ![]() yields for each j term
yields for each j term![]() , where
, where ![]() and
and ![]() are mere numerical coefficients corresponding to the respective
are mere numerical coefficients corresponding to the respective![]() . Whatever the numerical values of these coefficients might be, the space and time ranges appear separately: all
. Whatever the numerical values of these coefficients might be, the space and time ranges appear separately: all ![]() on the one side and
on the one side and ![]() on the other side can be put independently equal to zero to describe local or simultaneous events. The case
on the other side can be put independently equal to zero to describe local or simultaneous events. The case ![]() is conceptually different and more interesting, as the j-th term of (1.6) reads
is conceptually different and more interesting, as the j-th term of (1.6) reads![]() , being
, being ![]() and
and ![]() new numerical coefficients; the space and time ranges appear together in the mixed term
new numerical coefficients; the space and time ranges appear together in the mixed term ![]() with mixed coefficient
with mixed coefficient![]() . In general all higher order terms of the sum over
. In general all higher order terms of the sum over ![]() imply mixed space time ranges.
imply mixed space time ranges.
Hence the first order and second order terms of the series do not imply merely two different degrees of numerical approximations in calculating ![]() of the Equation (1.5). It is clear that
of the Equation (1.5). It is clear that ![]() is the classical case: a glance to this equation indicates that space and time terms are in fact separate dynamical variables like in (1.1). In the linear combination (1.1) the time is an independent input parameter, arbitrarily set, as a function of which the x-coordinate is next calculable consistently with any event occurring in the system, e.g. the interaction between particles. But in general the mixed terms modify strongly this point of view; for example it is no longer possible to put
is the classical case: a glance to this equation indicates that space and time terms are in fact separate dynamical variables like in (1.1). In the linear combination (1.1) the time is an independent input parameter, arbitrarily set, as a function of which the x-coordinate is next calculable consistently with any event occurring in the system, e.g. the interaction between particles. But in general the mixed terms modify strongly this point of view; for example it is no longer possible to put ![]() independently of
independently of![]() : simultaneity and locality are in general conflicting concepts.
: simultaneity and locality are in general conflicting concepts.
Moreover the Equation (1.6) introduces contextually the concept of evolution regarding in the same way also the initial configuration of the system through products of ranges![]() . So (1.6) shows that the local space and time coordinates separately measured and purposely introduced to carry out best fit calculations are actually mere mathematical parameters useful for empirical calculations only; the space time ranges of coordinates are instead physical parameters collecting together sets of local space coordinates
. So (1.6) shows that the local space and time coordinates separately measured and purposely introduced to carry out best fit calculations are actually mere mathematical parameters useful for empirical calculations only; the space time ranges of coordinates are instead physical parameters collecting together sets of local space coordinates ![]() included within
included within ![]() that define the evolution of allowed states of physical systems during a finite time lapse
that define the evolution of allowed states of physical systems during a finite time lapse![]() . Without this correlation, the system would be that of the matrix (1.2), i.e. describable as if it would consist of a list of mathematical terms unrelated and disconnected each other at various times.
. Without this correlation, the system would be that of the matrix (1.2), i.e. describable as if it would consist of a list of mathematical terms unrelated and disconnected each other at various times.
This is the first hint to reproduce the coefficients ![]() of (1.1) from first principles, thus overcoming both empiricism and Wigner’s doubts.
of (1.1) from first principles, thus overcoming both empiricism and Wigner’s doubts.
In effect it will be found in the following that![]() , not the local
, not the local![]() , is a sensible definition of space time compatible with quantum requirements. This shows that (1.6) lays prospectively the basis of both relativity and quantum physics: the necessity of a space time frame defined via sets of local coordinates
, is a sensible definition of space time compatible with quantum requirements. This shows that (1.6) lays prospectively the basis of both relativity and quantum physics: the necessity of a space time frame defined via sets of local coordinates ![]() is in principle also consistent with the quantum lack of determinism based on local coordinates both exactly knowable.
is in principle also consistent with the quantum lack of determinism based on local coordinates both exactly knowable.
Anyway, apart from mathematical details, the known value of any ![]() in (1.2) is still reproducible in principle solving once more a set of linear equations of the unknown
in (1.2) is still reproducible in principle solving once more a set of linear equations of the unknown![]() . The expected rationality inherent the best fit calculation appears now through the mathematical properties of
. The expected rationality inherent the best fit calculation appears now through the mathematical properties of![]() . With a correct choice of this function, the coefficients
. With a correct choice of this function, the coefficients ![]() describe conceptually and not only mathematically the evolution of physical systems; in practice this function still maps the systems like the mere empirical approach (1.2) and makes plausible the numerical representation of the reality. The key point is the underlying link with the concept of time evolution of physical systems with respect to their initial conditions.
describe conceptually and not only mathematically the evolution of physical systems; in practice this function still maps the systems like the mere empirical approach (1.2) and makes plausible the numerical representation of the reality. The key point is the underlying link with the concept of time evolution of physical systems with respect to their initial conditions.
Thus the basic idea is that a general function, ![]() , must exist able to describe specific events of interest implementing the holistic concept of system evolution: if it is true that the Nature is a complex system under continuous modification, then the physical laws should also conform themselves to this principle. Accordingly, space and time should appear as inseparable properties in this evolutionary scenario that also implies the holistic view previously outlined as actual mathematical requirement.
, must exist able to describe specific events of interest implementing the holistic concept of system evolution: if it is true that the Nature is a complex system under continuous modification, then the physical laws should also conform themselves to this principle. Accordingly, space and time should appear as inseparable properties in this evolutionary scenario that also implies the holistic view previously outlined as actual mathematical requirement.
On the one hand if the function ![]() would be known, then there would be no necessity of determining in advance via best fit approach the power series (1.6) of the dynamical variables, which in fact would be calculable themselves through
would be known, then there would be no necessity of determining in advance via best fit approach the power series (1.6) of the dynamical variables, which in fact would be calculable themselves through ![]() and its derivatives; this chance exemplifies in principle the starting question of this section, i.e. to show why the rational knowledge of phenomena allows mapping the reality into numbers regardless of speculations about the geometrical origin of
and its derivatives; this chance exemplifies in principle the starting question of this section, i.e. to show why the rational knowledge of phenomena allows mapping the reality into numbers regardless of speculations about the geometrical origin of![]() . On the other hand this conclusion introduces the aim of the present paper, i.e. to understand how an appropriate function representing the physical phenomena through the concept of holistic evolution in fact prospects a conceptual path alternative to empirical best fit calculations; in this way
. On the other hand this conclusion introduces the aim of the present paper, i.e. to understand how an appropriate function representing the physical phenomena through the concept of holistic evolution in fact prospects a conceptual path alternative to empirical best fit calculations; in this way ![]() also removes the necessity of knowing in advance case by case the specific event to be described. Therefore the previous question about the mathematical structure of the reality overlaps to the following ones: “how all information codified in physical formulas is in fact deducible from
also removes the necessity of knowing in advance case by case the specific event to be described. Therefore the previous question about the mathematical structure of the reality overlaps to the following ones: “how all information codified in physical formulas is in fact deducible from![]() ?” and also “are the current results of such theoretical basis susceptible of predictive outcomes prospecting the possible future Universe”?
?” and also “are the current results of such theoretical basis susceptible of predictive outcomes prospecting the possible future Universe”?
Clearly the second question concerns the development of science and has heuristic valence in describing anything effectively allowed to happen in a changing Universe.
The purpose of the present paper is to highlight some straightforward hints towards this aim, i.e. how in principle could a single function ![]() describe all variety of phenomena occurring in the Universe.
describe all variety of phenomena occurring in the Universe.
For simplicity and brevity of exposition the model is deliberately one dimensional: this choice does not represent a conceptual limit, it merely aims to simplify the theoretical approach with mathematical formalism as simple as possible. Also, the model purposely considers scalar quantities: for example v is the component of the velocity vector![]() ; analogous consideration holds for the component p of the momentum
; analogous consideration holds for the component p of the momentum![]() . These positions allow writing only
. These positions allow writing only ![]() without subscripts. The time evolution of this function in a given R is therefore given by
without subscripts. The time evolution of this function in a given R is therefore given by![]() .
.
To add a further step forwards, consider more closely the particular space time interval introduced by (1.6)
![]() (1.7)
(1.7)
as ![]() consists of two ranges, the first problem is how to define position and size of both
consists of two ranges, the first problem is how to define position and size of both ![]() and
and ![]() in an appropriate reference system R. For example the coordinates
in an appropriate reference system R. For example the coordinates ![]() and
and ![]() can be defined in order to fix the distances of one boundary of
can be defined in order to fix the distances of one boundary of ![]() and
and ![]() on the respective axes, e.g.
on the respective axes, e.g. ![]() and
and![]() , from their common origin O of R, imagined as a two dimensional space time plane with the time on the vertical axis and the length on the horizontal axis; so
, from their common origin O of R, imagined as a two dimensional space time plane with the time on the vertical axis and the length on the horizontal axis; so ![]() and
and ![]() fix the sizes of the ranges. However a better chance exists in this respect: it is possible to introduce the following average values calculated via the boundary coordinates themselves of the ranges only
fix the sizes of the ranges. However a better chance exists in this respect: it is possible to introduce the following average values calculated via the boundary coordinates themselves of the ranges only
![]() (1.8)
(1.8)
To describe self-consistently size and position of ![]() and
and ![]() in the space time plane, these mean values are defined on the respective axes of R as follows
in the space time plane, these mean values are defined on the respective axes of R as follows
![]() (1.9)
(1.9)
the first definition relates ![]() to the average time
to the average time ![]() needed for a hypothetical particle to travel through the whole range size, whatever it might be, the second definition relates
needed for a hypothetical particle to travel through the whole range size, whatever it might be, the second definition relates ![]() to the displacement rate of its average coordinate
to the displacement rate of its average coordinate ![]() related to the position of both range boundaries only. Clearly these definitions need introducing two velocities
related to the position of both range boundaries only. Clearly these definitions need introducing two velocities ![]() and
and ![]() compliant with the strategy of having defined mean values characteristic of both ranges only; if indeed just these definitions characterize size and position of both ranges in a self-consistent way, then any reference to O, and thus to R, is lost. In other words, replacing (1.9) into (1.7) neither
compliant with the strategy of having defined mean values characteristic of both ranges only; if indeed just these definitions characterize size and position of both ranges in a self-consistent way, then any reference to O, and thus to R, is lost. In other words, replacing (1.9) into (1.7) neither ![]() nor
nor ![]() appear anymore explicitly in
appear anymore explicitly in![]() : these mean values of coordinates are in effect identically compatible with different
: these mean values of coordinates are in effect identically compatible with different ![]() and
and![]() , i.e. with any other
, i.e. with any other![]() . Multiplying now side by side (1.9), one finds
. Multiplying now side by side (1.9), one finds ![]() i.e.
i.e.
![]() (1.10)
(1.10)
The actual value of ![]() does not require in principle any specific hypothesis; is however interesting its particular value, necessarily constant without contradicting (1.10), consistent with
does not require in principle any specific hypothesis; is however interesting its particular value, necessarily constant without contradicting (1.10), consistent with ![]() and
and ![]() regardless of the reference system R where are defined
regardless of the reference system R where are defined ![]() and
and![]() ; the expression at the right hand side, formally identical to that at the left hand side, can be referred indeed to another reference system
; the expression at the right hand side, formally identical to that at the left hand side, can be referred indeed to another reference system![]() . It is significant that a unique constant
. It is significant that a unique constant ![]() fits different time and space coordinates and that this equation implies different time and space ranges in different inertial reference systems R and
fits different time and space coordinates and that this equation implies different time and space ranges in different inertial reference systems R and ![]() even in reciprocal motion.
even in reciprocal motion.
However, the fact that space time terms ![]() more complex than that of (1.7) also appear in (1.6), suggests that a more complex space time metric is to be expected too. Since now all of these hints seem a reasonable step towards the special and general relativity. This also suggests that a model prospectively aimed to account someway for these suggestions should consider since the beginning not only
more complex than that of (1.7) also appear in (1.6), suggests that a more complex space time metric is to be expected too. Since now all of these hints seem a reasonable step towards the special and general relativity. This also suggests that a model prospectively aimed to account someway for these suggestions should consider since the beginning not only ![]() and
and ![]() but also, at least,
but also, at least, ![]() and
and![]() . Thus the problem is how to handle methodically both changes
. Thus the problem is how to handle methodically both changes ![]() and
and![]() , rather than
, rather than ![]() itself, to describe systematically the physical properties of any system concerned by
itself, to describe systematically the physical properties of any system concerned by![]() . Despite
. Despite ![]() is not known, are essential and enough to this purpose the general definitions
is not known, are essential and enough to this purpose the general definitions
![]() (1.11)
(1.11)
and, increasing again ![]() by
by ![]() and
and ![]() by
by![]() ,
,
![]() (1.12)
(1.12)
the former defines![]() , the latter
, the latter![]() . Note that being by definition
. Note that being by definition
![]()
where ![]() is any descriptive parameter of a physical system in the sense previously introduced, it is possible to put at the first order of approximation
is any descriptive parameter of a physical system in the sense previously introduced, it is possible to put at the first order of approximation
![]()
neglecting the higher order terms.
Here and in the following x and ![]() symbolize the r-th space coordinate of each j-th particle of the system and its change as a function of
symbolize the r-th space coordinate of each j-th particle of the system and its change as a function of ![]() upon which depend possible changes of all dynamical variables and their x-components, e.g.
upon which depend possible changes of all dynamical variables and their x-components, e.g. ![]() and
and![]() ; the same holds for
; the same holds for ![]() and
and![]() , and so on. Although is considered for brevity and simplicity of notation one dimensional space coordinate only, from a conceptual point of view the number of actual coordinates is not necessarily limited to the usual three currently accepted.
, and so on. Although is considered for brevity and simplicity of notation one dimensional space coordinate only, from a conceptual point of view the number of actual coordinates is not necessarily limited to the usual three currently accepted.
The remainder of the paper concerns these points through an “ab initio” theoretical model whose exposition aims to be as self-contained as possible. Such model aims to deduce both well known results, as a validation, and new achievements, as innovative implications: in both cases, however, the assessment benchmark is its conceptual root in the Equations (1.11) and (1.12) only.
Despite for sake of brevity and clarity of exposition physical properties like energy and momentum have been taken for granted and explicitly mentioned as well acknowledged concepts in this introductory section, actually all of them will be inferred self-consistently themselves uniquely through (1.11) and (1.12); this holds also for quantities like charge and mass that apparently have nothing to do with the concept of evolution defined by these equations. Although seemingly trivial and innocuous, these two equations are unique source of information and unique input enough to infer all considerations exposed below in a consequential way, while overcoming Wigner’s doubts and renouncing to any hints from physics theories currently existing. For completeness, when necessary, are also shortly sketched some results previously published to emphasize their connection with the present conceptual frame.
2. The Model
To infer information of physical interest from the initial positions (1.11) and (1.12), the simplest idea is to relate appropriately ![]() and
and![]() , and possibly even
, and possibly even ![]() and
and![]() , to
, to ![]() and
and ![]() in an arbitrary R. In principle this correlation can be expressed implementing
in an arbitrary R. In principle this correlation can be expressed implementing ![]() to obtain two identities
to obtain two identities ![]() that merge into
that merge into
![]() (2.1)
(2.1)
The ratio at the left hand side introduces a new concept implied by![]() , the velocity v; this dynamical variable, not evident nor necessary in (1.11) and (1.12), is defined by the identity
, the velocity v; this dynamical variable, not evident nor necessary in (1.11) and (1.12), is defined by the identity
![]() (2.2)
(2.2)
The significance of this result, which follows the Equation (1.11) only, appears rewriting both sides according to the Equation (1.12) i.e. implementing likewise the identity![]() . Dividing both sides by
. Dividing both sides by ![]() still via
still via ![]() just introduced, an analogous reasoning yields the further identity
just introduced, an analogous reasoning yields the further identity
![]() (2.3)
(2.3)
The explicit physical meaning of these identities appears when![]() , i.e. when the range sizes described by
, i.e. when the range sizes described by ![]() tend to zero. On the one hand this is possible because no restrictive hypothesis has been introduced about the ranges, on the other hand
tend to zero. On the one hand this is possible because no restrictive hypothesis has been introduced about the ranges, on the other hand ![]() and
and ![]() do not necessarily imply equal limits
do not necessarily imply equal limits ![]() and
and ![]() of the Equations (1.11). As written, the left hand side of (2.3) reads
of the Equations (1.11). As written, the left hand side of (2.3) reads![]() , whereas the right hand side reads
, whereas the right hand side reads![]() . The limits of these expressions for
. The limits of these expressions for ![]() are indeed
are indeed ![]() and
and![]() ; as such, they are defined in general by the local analytical dependence of
; as such, they are defined in general by the local analytical dependence of ![]() upon either dynamical variable.
upon either dynamical variable.
All this makes sense, as in fact the symbols ![]() indicate arbitrary changes not only of
indicate arbitrary changes not only of ![]() but also of x and t; just for this reason, therefore, nothing can be “a priori” inferred from the ratios between
but also of x and t; just for this reason, therefore, nothing can be “a priori” inferred from the ratios between ![]() and
and ![]() or
or ![]() since both these latter are arbitrary, unknown, unrelated and thus implementable separately and independently each other. Instead, despite (2.3) is trivial identity,
since both these latter are arbitrary, unknown, unrelated and thus implementable separately and independently each other. Instead, despite (2.3) is trivial identity,
![]() (2.4)
(2.4)
has physical meaning while the aforesaid limits imply contextually![]() ; the notation remarks that
; the notation remarks that ![]() yields in particular the local analytical form of
yields in particular the local analytical form of ![]() resulting from the specific correlations of
resulting from the specific correlations of ![]() with
with ![]() and
and ![]() (2.2) and (2.3). So the local behavior in the infinitesimal space range
(2.2) and (2.3). So the local behavior in the infinitesimal space range ![]() and time range
and time range ![]() fulfills at any
fulfills at any ![]() just the Equation (2.4). All quantities concerned by
just the Equation (2.4). All quantities concerned by ![]() are arbitrary and finite by definition; thus they have been handled, and will be again handled also in the following, according to standard algebraic rules likewise any finite dynamical variable. Instead the limits
are arbitrary and finite by definition; thus they have been handled, and will be again handled also in the following, according to standard algebraic rules likewise any finite dynamical variable. Instead the limits ![]() imposed to them define a further local condition/constrain that in fact eliminates their total arbitrariness and thus implies the mutual interdependence of both sides of (2.3) around a common limit: the initial analytic form of
imposed to them define a further local condition/constrain that in fact eliminates their total arbitrariness and thus implies the mutual interdependence of both sides of (2.3) around a common limit: the initial analytic form of![]() , whatever it might be, turns locally into that,
, whatever it might be, turns locally into that, ![]() , fulfilling both local limits. In this specific case one has found the D’Alembert equation describing the dynamics of a homogeneous elastic string vibrating with fixed extremities and with constant propagation rate v of the perturbation around the equilibrium position of the string. Obviously the local dependence of
, fulfilling both local limits. In this specific case one has found the D’Alembert equation describing the dynamics of a homogeneous elastic string vibrating with fixed extremities and with constant propagation rate v of the perturbation around the equilibrium position of the string. Obviously the local dependence of ![]() upon x and t is found by solving the resulting differential equation.
upon x and t is found by solving the resulting differential equation.
This first example has emphasized how to infer information about one specific physical system through the local extrapolation ![]() of
of ![]() as a function of both
as a function of both ![]() and
and![]() . Although the Equations (2.3) and (2.4) have identical analytical form, they remark the transition from non-local to local description of the concerned physical system: the former is in fact non-calculable, being mere identity, the latter takes physical meaning because is calculable and comparable with the experience. Otherwise stated, it is reductive to regard (2.3) as intermediate algebraic step towards (2.4); it actually describes a non-real and non-local world that does not have identifiable physical properties of the real and local world accessible to the experiment. Non-locality and non-reality are concurrent features of a further world, the quantum world, that can be not only guessed but also implemented to understand the microscopic properties of matter.
. Although the Equations (2.3) and (2.4) have identical analytical form, they remark the transition from non-local to local description of the concerned physical system: the former is in fact non-calculable, being mere identity, the latter takes physical meaning because is calculable and comparable with the experience. Otherwise stated, it is reductive to regard (2.3) as intermediate algebraic step towards (2.4); it actually describes a non-real and non-local world that does not have identifiable physical properties of the real and local world accessible to the experiment. Non-locality and non-reality are concurrent features of a further world, the quantum world, that can be not only guessed but also implemented to understand the microscopic properties of matter.
It is easy to generalize this result to the case where the string is non-homogeneous simply considering another possible chance of defining the link between ![]() and both
and both ![]() and
and ![]() via the trial positions
via the trial positions ![]() and
and![]() , i.e. introducing two different proportionality factors
, i.e. introducing two different proportionality factors ![]() and
and ![]() concerning separately the previous
concerning separately the previous ![]() and
and![]() . In this case
. In this case ![]() is defined via these generalized increments, both still unknown and arbitrary of course, where however the functions
is defined via these generalized increments, both still unknown and arbitrary of course, where however the functions ![]() and
and ![]() prospect a new result even more general than (2.3). Now let us repeat the previous steps. To modify the correlation of
prospect a new result even more general than (2.3). Now let us repeat the previous steps. To modify the correlation of ![]() upon
upon ![]() and
and ![]() via the respective factors
via the respective factors ![]() and
and![]() , multiply first both sides of (2.2) by
, multiply first both sides of (2.2) by![]() , still keeping the definition
, still keeping the definition ![]() although with a different expectation value of the resulting local v. So the identity
although with a different expectation value of the resulting local v. So the identity
![]() (2.5)
(2.5)
yields the further identity according to (1.12)
![]() (2.6)
(2.6)
and thus, dividing both sides by![]() ,
,
![]() (2.7)
(2.7)
formally the Equation (2.7) results from two steps, taking first the changes (2.6) of the quantities at both sides of (2.5), which are subsequently related to ![]() and
and ![]() to obtain (2.7). Of course the limit
to obtain (2.7). Of course the limit ![]() is not implemented at this intermediate step, as this would mean differentiating the quantities at both sides before having introduced the second function
is not implemented at this intermediate step, as this would mean differentiating the quantities at both sides before having introduced the second function![]() ; instead it is convenient to keep still finite changes of
; instead it is convenient to keep still finite changes of ![]() and
and![]() , which again can be further worked out regarding them like any finite physical variable, to introduce
, which again can be further worked out regarding them like any finite physical variable, to introduce ![]() too. Write thus without loss of generality
too. Write thus without loss of generality
![]() (2.8)
(2.8)
being ![]() a constant velocity by definition; therefore
a constant velocity by definition; therefore
![]() (2.9)
(2.9)
Now it is possible to infer from the Equation (2.9) the pertinent differential equation once more via the position ![]() that implies thus a new local function
that implies thus a new local function![]() , i.e.
, i.e.
![]() (2.10)
(2.10)
The particular result with![]() , which thus can be included in
, which thus can be included in ![]() at left hand side, yields the well known equation of the wave propagating through a non-homogeneous string with one fixed extremity. Obviously the functions
at left hand side, yields the well known equation of the wave propagating through a non-homogeneous string with one fixed extremity. Obviously the functions ![]() and
and ![]() fulfilling the respective local limits implied by (2.4) and (2.10) are different; is indeed different the local behavior of either function correspondingly to the respective differential equations. The notation emphasizes that
fulfilling the respective local limits implied by (2.4) and (2.10) are different; is indeed different the local behavior of either function correspondingly to the respective differential equations. The notation emphasizes that![]() : these functions describe different physical systems because of the different correlation of
: these functions describe different physical systems because of the different correlation of ![]() with
with ![]() and
and![]() .
.
The outcomes (2.4) and (2.10) highlight the strategy of the present paper: the arbitrary function ![]() initially introduced according to (1.4) to describe in principle the physical properties of any system is implementable in various ways, depending on how is expressed the possible correlation between its change
initially introduced according to (1.4) to describe in principle the physical properties of any system is implementable in various ways, depending on how is expressed the possible correlation between its change ![]() with respect to that of its dynamical variables
with respect to that of its dynamical variables ![]() and
and![]() . In other words the crucial point is not the analytical form of
. In other words the crucial point is not the analytical form of![]() , but how it changes as a function of
, but how it changes as a function of ![]() and
and![]() : whatever
: whatever ![]() might be, in fact this procedure identifies itself the possible kind of problem and outlines its mathematical solution as well via the resulting differential equation.
might be, in fact this procedure identifies itself the possible kind of problem and outlines its mathematical solution as well via the resulting differential equation.
These results are not accidental outcomes inherent the explanatory examples just carried out; in effect no “ad hoc” hypotheses have been made on the concerned systems, e.g. homogeneous or non-homogeneous string, having simply introduced two different ways of describing the local change, i.e. the evolution, of![]() .
.
Let us exemplify further possible ways to handle ![]() and
and ![]() to confirm further the general worth of this strategy. To this purpose multiply both sides of (2.9) by
to confirm further the general worth of this strategy. To this purpose multiply both sides of (2.9) by ![]() so that
so that
![]() (2.11)
(2.11)
which suggests the following definitions according to (2.8)
![]() (2.12)
(2.12)
As the unique Equation (2.9) cannot specify both ![]() and
and![]() , which are still undefined, nothing excludes in principle the chances
, which are still undefined, nothing excludes in principle the chances ![]() or
or![]() . Yet, even so, it appears that the positions (2.12) are not merely formal. To understand the physical meaning of the “new” quantities p and
. Yet, even so, it appears that the positions (2.12) are not merely formal. To understand the physical meaning of the “new” quantities p and![]() , note that the first equation implies
, note that the first equation implies
![]() (2.13)
(2.13)
By definition ![]() and
and![]() , whereas
, whereas ![]() and
and![]() ; of course all quantities labeled “1” and “2” are arbitrary. As it possible to multiply side by side these equations, write
; of course all quantities labeled “1” and “2” are arbitrary. As it possible to multiply side by side these equations, write ![]() . Intuitively
. Intuitively ![]() should read
should read ![]() with notation that avoids confusion between
with notation that avoids confusion between ![]() and
and![]() : in effect if
: in effect if ![]() is specifically regarded as mean value within its own allowed range
is specifically regarded as mean value within its own allowed range ![]() of variability, i.e.
of variability, i.e.![]() , one finds
, one finds ![]() whatever
whatever ![]() and
and ![]() might be. The same reasoning for
might be. The same reasoning for ![]() yields
yields![]() . The idea of local variables
. The idea of local variables ![]() and
and ![]() allows an interesting implication noting that in general
allows an interesting implication noting that in general![]() ; so merging (2.13) one finds
; so merging (2.13) one finds
![]() (2.14)
(2.14)
i.e.![]() . Also, since
. Also, since![]() , then
, then
![]() (2.15)
(2.15)
To examine either chance, calculate with the help of (2.12), (2.2) and (2.9)
![]() (2.16)
(2.16)
Regarding separately the addends at the initial and final left and right hand sides, this chain of equations is consistent: ![]() and pv at the left hand side correspond respectively to
and pv at the left hand side correspond respectively to ![]() and
and![]() ; in effect
; in effect ![]() is nothing else but (2.13) with
is nothing else but (2.13) with![]() . This justifies regarding p and
. This justifies regarding p and ![]() of (2.16) as momentum and energy in agreement with (2.23). Yet another chance also consistent with
of (2.16) as momentum and energy in agreement with (2.23). Yet another chance also consistent with ![]() is
is
![]() (2.17)
(2.17)
i.e. ![]() so that
so that![]() : in effect v is actually velocity component defined by
: in effect v is actually velocity component defined by ![]() during the time range
during the time range![]() .
.
The well known Equation (2.15) will be inferred again later; these short notes aim to justify preliminarily the positions (2.12) according which, regarding from now on ![]() with usual notation, p and
with usual notation, p and ![]() are nothing else but momentum and energy of a relativistic free particle. Simply regarding p and
are nothing else but momentum and energy of a relativistic free particle. Simply regarding p and ![]() as local random values in their allowed ranges
as local random values in their allowed ranges ![]() and
and![]() , i.e. anticipating here the concept of quantum uncertainty, it also appears in (2.14) why
, i.e. anticipating here the concept of quantum uncertainty, it also appears in (2.14) why ![]() must be upper bound: if not, then p necessarily finite in its finite range
must be upper bound: if not, then p necessarily finite in its finite range ![]() could be consistent with an infinite energy
could be consistent with an infinite energy ![]() allowed by diverging
allowed by diverging ![]() once multiplied by a value of
once multiplied by a value of![]() .
.
So the finite value of c follows as a corollary.
Also, it is not surprising that the energy is defined an arbitrary constant apart; it will be shown shortly, however, that the constant has in this context a peculiar physical meaning. If![]() , then
, then ![]() and thus
and thus ![]() i.e.
i.e.![]() . The implications of this chance will be examined in the following.
. The implications of this chance will be examined in the following.
2.1. Diffusion Equations
With![]() , according to (2.8), the Equation (2.11) reads
, according to (2.8), the Equation (2.11) reads
![]() (2.18)
(2.18)
since it is certainly possible to introduce an arbitrary function g such that![]() , being
, being ![]() a time dimensional constant, this equation reads
a time dimensional constant, this equation reads
![]() (2.19)
(2.19)
Whatever the function ![]() might be, D has physical dimensions of diffusion coefficient; in effect with the position
might be, D has physical dimensions of diffusion coefficient; in effect with the position![]() , which implies the local behavior of
, which implies the local behavior of ![]() described by
described by![]() , the last equation reads
, the last equation reads
![]() (2.20)
(2.20)
This is just the general form of diffusion equation in a homogeneous and isotropic medium in the absence of internal sources or sinks. But diffusion of what? Although ![]() is by definition dimensionless function, two relevant examples are reported below. To this purpose are anticipated here for clarity the concepts of mass and energy kT; both concepts will be inferred later self consistently in the frame of the present theoretical model.
is by definition dimensionless function, two relevant examples are reported below. To this purpose are anticipated here for clarity the concepts of mass and energy kT; both concepts will be inferred later self consistently in the frame of the present theoretical model.
It is possible to multiply ![]() at both sides by a constant mass per unit volume
at both sides by a constant mass per unit volume![]() ; so the equation
; so the equation
![]() (2.21)
(2.21)
where C is an appropriate function describing the local value of mass density, concerns the matter transport function under non-equilibrium concentration gradient. It is known that other important phenomena fulfill (2.20); in fact the extension to these cases, e.g. the Fourier heat diffusion, is also possible in an analogous way. Implementing a different dimensional factor to the local function![]() , i.e. multiplying both sides by an appropriate constant energy
, i.e. multiplying both sides by an appropriate constant energy![]() , one finds the famous equation
, one finds the famous equation
![]() (2.22)
(2.22)
where now with usual notation K replaces D to express the heat diffusion coefficient simply identifying![]() .
.
Note that the present strategy to infer information about physical systems reveals unexpected links between seemingly different laws: it is significant the fact that elementary manipulations of the equation of vibrating string lead to the diffusion equations.
2.2. Energy and Momentum
The Equation (2.8) reads according to (2.9)
![]() (2.23)
(2.23)
because of course the positions (2.12) still hold also in this particular case. This equation can be implemented in two ways.
The first way is
![]() (2.24)
(2.24)
and thus the second equality yields
![]() (2.25)
(2.25)
Here v still appears because the ratio ![]() is explicitly present in (2.24). The ranges explicitly written as
is explicitly present in (2.24). The ranges explicitly written as ![]() and
and ![]() by definition, where of course the quantities labeled with subscripts 1 and 2 are arbitrary, yield
by definition, where of course the quantities labeled with subscripts 1 and 2 are arbitrary, yield
![]()
this result reads therefore
![]() (2.26)
(2.26)
where p and ![]() are random values by definition included within the respective ranges.
are random values by definition included within the respective ranges.
The second way is highlighted rewriting (2.25) as
![]()
which yields
![]() (2.27)
(2.27)
the constant![]() , required to fulfill products of different variables, will be justified soon below; the notation emphasizes that
, required to fulfill products of different variables, will be justified soon below; the notation emphasizes that ![]() and
and ![]() are not constants. Thus, in agreement with (2.2), one also finds
are not constants. Thus, in agreement with (2.2), one also finds
![]() (2.28)
(2.28)
A few remarks help to simplify the notations in the following:
− the subscripts of ![]() and
and ![]() will be omitted as both ranges are arbitrary, so they actually symbolize any sizes of the respective
will be omitted as both ranges are arbitrary, so they actually symbolize any sizes of the respective ![]() and
and![]() ;
;
− the velocities v and c are profoundly different, as the former is defined as ratio of two range sizes whereas the latter is a universal constant of the Nature;
− the definitions of two “new” quantities, momentum p and energy![]() , have been guessed in (2.23) by dimensional reasons according to the constant
, have been guessed in (2.23) by dimensional reasons according to the constant![]() , once having defined dimensionless the coefficients
, once having defined dimensionless the coefficients ![]() and
and![]() .
.
The lack of specific assumptions on p and![]() , e.g. about the sizes of their allowed ranges, implies their physical definition on mere dimensional basis. At the moment n has been formally introduced in (2.27) as mere proportionality factor of a constant,
, e.g. about the sizes of their allowed ranges, implies their physical definition on mere dimensional basis. At the moment n has been formally introduced in (2.27) as mere proportionality factor of a constant,![]() ; dimensional reasons are enough to justify this position. In the following, see next Equations (3.1) and (3.2), it will be shown that n is actually an arbitrary integer, whereas the pertinent reasoning will also explain why the physical laws need quantization. The Equation (2.27) is particularly interesting as it correlates the products
; dimensional reasons are enough to justify this position. In the following, see next Equations (3.1) and (3.2), it will be shown that n is actually an arbitrary integer, whereas the pertinent reasoning will also explain why the physical laws need quantization. The Equation (2.27) is particularly interesting as it correlates the products ![]() and
and ![]() of four ranges of different dynamical variables, regardless of the necessity of the position
of four ranges of different dynamical variables, regardless of the necessity of the position ![]() and regardless of the range sizes; despite all changes of dynamical variables are arbitrary, the fact of having introduced a relationship between
and regardless of the range sizes; despite all changes of dynamical variables are arbitrary, the fact of having introduced a relationship between ![]() and
and ![]() implies the general and non-local character of this connection.
implies the general and non-local character of this connection.
Consider now the Equations (2.28) and (2.26): the former concerns ranges, the latter local values. Let us show that relevant physical information is obtainable merging these equations. Multiplying side by side
![]() (2.29)
(2.29)
one finds
![]() (2.30)
(2.30)
thus (2.30) is compatible with
![]() (2.31)
(2.31)
So follow three relevant equations
![]() (2.32)
(2.32)
Introduce now the boundary condition ![]() to which corresponds
to which corresponds![]() , because in general the third equation is different from zero; strictly speaking, in effect, there is no reason to expect that
, because in general the third equation is different from zero; strictly speaking, in effect, there is no reason to expect that ![]() is necessarily null too. So this boundary condition yields
is necessarily null too. So this boundary condition yields![]() ; moreover it implies defining a “new” quantity m not yet explicitly mentioned hitherto although implicitly inherent the physical dimensions of p and
; moreover it implies defining a “new” quantity m not yet explicitly mentioned hitherto although implicitly inherent the physical dimensions of p and![]() , i.e.
, i.e.
![]() (2.33)
(2.33)
so m is the rest mass. Calling c the constant velocity![]() , with usual notation, the last result reads thus
, with usual notation, the last result reads thus
![]() (2.34)
(2.34)
Clearly the particular case ![]() corresponds to
corresponds to![]() , which however requires
, which however requires ![]() in the second (2.34). It is immediate to verify that the two Equations (2.34) are consistent for
in the second (2.34). It is immediate to verify that the two Equations (2.34) are consistent for![]() , as they imply the Lorentz factor
, as they imply the Lorentz factor![]() , whereas it also follows
, whereas it also follows
![]() (2.35)
(2.35)
The second equation is compatible with![]() ; this is not surprising because actually the component of p along an arbitrary direction can have both signs. Much more interesting is the analogous conclusion for
; this is not surprising because actually the component of p along an arbitrary direction can have both signs. Much more interesting is the analogous conclusion for![]() , which implies states of negative and positive energy separated by a gap
, which implies states of negative and positive energy separated by a gap![]() .
.
Note that in addition to the concepts of mass, momentum and energy, follow from (1.11) and (1.12) the constancy of light speed and Lorentz transformations of energy and momentum.
A problem however arises now about why the first (2.34) is consistent with ![]() for
for ![]() whereas both (2.35) and the second (2.34) itself do not. A rational answer to this question will be given in the next Section 4.3. Note at the moment that the factor
whereas both (2.35) and the second (2.34) itself do not. A rational answer to this question will be given in the next Section 4.3. Note at the moment that the factor ![]() of (2.34) yields
of (2.34) yields![]() , being
, being ![]() an arbitrary reciprocal time; so, calling “wavelength” the new length
an arbitrary reciprocal time; so, calling “wavelength” the new length ![]() defined in this way and multiplying both sides of the first (2.34) by
defined in this way and multiplying both sides of the first (2.34) by![]() , one finds
, one finds![]() . Thus
. Thus
![]() (2.36)
(2.36)
where obviously![]() ; so
; so ![]() is defined even for
is defined even for![]() . These positions, here reasonably guessed, are easily verified starting again from (2.34) rewritten as
. These positions, here reasonably guessed, are easily verified starting again from (2.34) rewritten as![]() . With the help of (2.27), trivial manipulation turn equivalently this result into both forms
. With the help of (2.27), trivial manipulation turn equivalently this result into both forms
![]()
In both cases, dimensional considerations confirm the validity of the three positions (2.36), regarding in particular![]() : i.e. the range size
: i.e. the range size ![]() corresponds to one or more momentum wavelengths, the range size
corresponds to one or more momentum wavelengths, the range size ![]() corresponds to one or more frequency quanta. This suggests that actually
corresponds to one or more frequency quanta. This suggests that actually![]() , with
, with![]() , which formally is compatible with the constant appearing in (2.36) as
, which formally is compatible with the constant appearing in (2.36) as ![]() as in effect it has been guessed in (2.27). Therefore it is possible to write, in agreement with (2.2),
as in effect it has been guessed in (2.27). Therefore it is possible to write, in agreement with (2.2),
![]() (2.37)
(2.37)
It is interesting the fact that the Equations (2.36), pillars of quantum mechanics, are obtained contextually to the relativistic expressions of momentum, energy and rest mass.
2.3. Lagrange and Hamilton Equations
Write (2.28) as
![]()
rewriting left hand side via (2.27) with ![]() for simplicity, this equation reads then according to (2.23)
for simplicity, this equation reads then according to (2.23)
![]()
and thus
![]()
Also now the general concept of energy takes physical meaning via the limit![]() , which implies
, which implies ![]() as well; hence the result is
as well; hence the result is
![]() (2.38)
(2.38)
So ![]() is the particular local energy resulting from
is the particular local energy resulting from ![]() whose local behavior is described just by this equation. It is easy to realize that the resulting
whose local behavior is described just by this equation. It is easy to realize that the resulting ![]() turns out to be Lagrangian energy. The most intuitive interpretation of
turns out to be Lagrangian energy. The most intuitive interpretation of ![]() compatible with both sides of (2.38) is indeed
compatible with both sides of (2.38) is indeed
![]() (2.39)
(2.39)
as all of this is coherent with ![]() equal to energy, these equations define
equal to energy, these equations define ![]() reasonably consistent with the Lagrangian
reasonably consistent with the Lagrangian ![]() of a physical system. In effect defining
of a physical system. In effect defining
![]()
one finds
![]() (2.40)
(2.40)
in agreement with the well known definition of action S. Moreover, the second (2.39) yields
![]() (2.41)
(2.41)
owing to Euler’s theorem of homogeneous functions. Hence
![]() (2.42)
(2.42)
It is immediate to conclude that (2.42) yields the Hamilton function.
As the Equations (2.3) and (2.9) have sensible implications, (2.4) and (2.10), whereas (2.39) and (2.42) allow describing correctly the dynamics of any particle, the present approach appears significant: a relationship between space and time ranges ![]() and
and ![]() has been established even without knowing anything about the initial
has been established even without knowing anything about the initial![]() , simply admitting possible relationships between arbitrary
, simply admitting possible relationships between arbitrary ![]() and
and![]() . Once more, however, it is worth emphasizing that everything follows via (2.27) from (1.11) and (1.12) only.
. Once more, however, it is worth emphasizing that everything follows via (2.27) from (1.11) and (1.12) only.
Instead of attempting to explain some particular physical event on the basis of the intuition about its presumed theoretical foundation, we started from arbitrary changes of an introductory function, ![]() , which is not “a priori” specified but rather is “a posteriori” identified case by case depending on its possible local change described by the analytical form of the pertinent differential equation.
, which is not “a priori” specified but rather is “a posteriori” identified case by case depending on its possible local change described by the analytical form of the pertinent differential equation.
2.4. The Group Velocity
In (2.2) v is defined by the time range ![]() necessary for a particle to travel ideally the range size
necessary for a particle to travel ideally the range size![]() . Note now that (2.1) reads formally
. Note now that (2.1) reads formally
![]()
where ![]() and k are two “new” quantities called frequency and wave vector respectively; in this case the concept of velocity at the left hand side is different from that of (2.2). These definitions introduce a further concept of velocity, because at the local limit
and k are two “new” quantities called frequency and wave vector respectively; in this case the concept of velocity at the left hand side is different from that of (2.2). These definitions introduce a further concept of velocity, because at the local limit ![]() one finds
one finds
![]() (2.43)
(2.43)
It is immediate to show that also the positions (2.36), in particular the third one, allow calculating consistently the group velocity of a matter wave packet through the following simple chain of equations. Implementing ![]() and
and ![]() with the help of (2.28) one finds
with the help of (2.28) one finds
![]() (2.44)
(2.44)
whatever ![]() might be. This suggest a possible quantum definition of velocity additional to the direct ratio between space range
might be. This suggest a possible quantum definition of velocity additional to the direct ratio between space range ![]() and time range
and time range![]() . Once more the position
. Once more the position ![]() implies the local definitions
implies the local definitions ![]() and
and![]() , whereas v turns to the first equality into local group velocity
, whereas v turns to the first equality into local group velocity![]() , i.e.
, i.e.
![]() (2.45)
(2.45)
Eventually, note that the third Equation (2.36) alone is enough itself to confirm this result. Write
![]() (2.46)
(2.46)
as![]() , trivial manipulations yield
, trivial manipulations yield
![]()
whence
![]()
Therefore
![]()
yields for ![]() the local dispersion equation
the local dispersion equation
![]() (2.47)
(2.47)
i.e. the well known group velocity of a matter packet wave.
In summary, relevant equations of physics are simply inferred and described through various chances of changing an arbitrary function ![]() of time and space, regardless of its early specific physical meaning and without need of introducing initial hypotheses. This concerns crucially the functions
of time and space, regardless of its early specific physical meaning and without need of introducing initial hypotheses. This concerns crucially the functions ![]() and
and ![]() introduced in general in (2.8) and (2.9), whose specific analytical form determines the correlation of
introduced in general in (2.8) and (2.9), whose specific analytical form determines the correlation of ![]() with
with ![]() and
and![]() : as it has been just highlighted, if
: as it has been just highlighted, if ![]() in (2.9) then one obtains the diffusion Equation (2.10), if instead
in (2.9) then one obtains the diffusion Equation (2.10), if instead ![]() then one obtains further results concerned later thanks to the additional freedom degree allowed to
then one obtains further results concerned later thanks to the additional freedom degree allowed to![]() .
.
2.5. The Relativistic Velocity
The starting point is the first Equation (2.34), which must be rearranged in order to find a sum rule between two arbitrary velocities ![]() and their corresponding
and their corresponding ![]() and
and![]() , e.g. in two different inertial reference systems R and
, e.g. in two different inertial reference systems R and![]() . As
. As![]() , calculate first
, calculate first
![]()
in this way one has introduced ![]() through the invariant momentum. It is necessary now to define in general
through the invariant momentum. It is necessary now to define in general ![]() in a form suitable to relate
in a form suitable to relate ![]() and
and![]() , e.g. in another reference system. A reasonable position is the following linear combination that does not involve neither
, e.g. in another reference system. A reasonable position is the following linear combination that does not involve neither ![]() nor
nor![]() , i.e.
, i.e.
![]()
so that the sought result is
![]() (2.48)
(2.48)
Accordingly any v summed to or subtracted from c still yields c.
3. Preliminary Implications of the Model
The results so far obtained are enough to get four relevant consequences, exposed below.
3.1. Statistical Formulation of Quantum Uncertainty
Write (2.27) as
![]() (3.1)
(3.1)
being n an arbitrary integer. The reason of this definition is to make (2.27) independent of a specific reference system. Suppose that (3.1) holds for ranges defined in R whereas ![]() holds for that defined in any
holds for that defined in any![]() , with
, with ![]() arbitrary integer as well; the prime symbols account for the respective Lorentz transformations of range sizes. Actually the reference systems are indistinguishable because neither n nor
arbitrary integer as well; the prime symbols account for the respective Lorentz transformations of range sizes. Actually the reference systems are indistinguishable because neither n nor ![]() are specific numbers, they instead symbolize by definition whole sets of allowed integer numbers: so any specific n of the first set that turns into a new specific
are specific numbers, they instead symbolize by definition whole sets of allowed integer numbers: so any specific n of the first set that turns into a new specific ![]() of the primed set does not imply in fact distinguishable sets of the respective reference systems. This point is better understood introducing appropriate measure units
of the primed set does not imply in fact distinguishable sets of the respective reference systems. This point is better understood introducing appropriate measure units ![]() to express the respective range sizes; for example it is possible to express the size of
to express the respective range sizes; for example it is possible to express the size of ![]() as
as![]() ; i.e.
; i.e. ![]() is a dimensionless length expressing the actual range size in
is a dimensionless length expressing the actual range size in ![]() units.
units.
Is evident the hint to the well known Planck units, whose choice implies ![]() by definition. Without having introduced the gravity constant yet, this explicit reference appears here premature; it is enough to emphasize that the Planck units fulfill this equation by definition. The crucial fact is that introducing the dimensionless lengths
by definition. Without having introduced the gravity constant yet, this explicit reference appears here premature; it is enough to emphasize that the Planck units fulfill this equation by definition. The crucial fact is that introducing the dimensionless lengths![]() , the couples
, the couples ![]() and
and ![]() fulfill the condition
fulfill the condition![]() . In this way, dividing side by side with the Equations (3.1), one finds
. In this way, dividing side by side with the Equations (3.1), one finds
![]()
It implies that with this choice of measure units, the statistical formulation of quantum uncertainty reads simply
![]() (3.2)
(3.2)
the stars indicate arbitrary real numbers, n is instead an arbitrary real integer number. This reasoning shows that in fact the Equations (2.27) hold regardless of any reference system; otherwise stated, the problem of specifying the reference system where are defined the four uncertainty ranges is physically meaningless, provided that the local dynamical variables are systematically replaced by respective uncertainty range totally unknown in any physical problem. This holds also for the derivatives, which are defined in the present model as mere ratios of uncertainty ranges arbitrary, unknown and conceptually unknowable: for example is meaningless to inquire whether ![]() refers to Cartesian or curvilinear or cylindrical reference frame. What is crucial in this reasoning is that the four starred numbers be not specifiable and unspecified in any physical problem formulated via the Equations (2.10); in short, the quantization of n is necessary to make (3.1) independent of any specific R. For clarity and self-contained exposition, this is shortly sketched in the next subsection. The results quoted here for completeness are reported more in detail elsewhere [4] [5] .
refers to Cartesian or curvilinear or cylindrical reference frame. What is crucial in this reasoning is that the four starred numbers be not specifiable and unspecified in any physical problem formulated via the Equations (2.10); in short, the quantization of n is necessary to make (3.1) independent of any specific R. For clarity and self-contained exposition, this is shortly sketched in the next subsection. The results quoted here for completeness are reported more in detail elsewhere [4] [5] .
3.2. The Old Quantum Mechanics
It is usually assumed that the quantum problems are tackled via the operator formalism of wave mechanics, introducing operators and wave equations. For comparison purposes, this section sketches very shortly results concerning one case where the wave equation can be exactly solved: the non relativistic hydrogenlike atom. The aim is to show that identical information is obtainable via a a “corpuscular approach”, which does not require solving any wave equation; it is enough to replace ![]() and
and![]() , instead of
, instead of![]() , and proceed via elementary algebraic manipulations. These results help understanding how the relativity fits the conceptual frame so far outlined.
, and proceed via elementary algebraic manipulations. These results help understanding how the relativity fits the conceptual frame so far outlined.
The starting point is the classical component of ![]() along an arbitrary direction defined by the unit vector
along an arbitrary direction defined by the unit vector ![]() is
is![]() . Consider thus
. Consider thus
![]()
which introduces a range of possible values for ![]() included in
included in![]() . If
. If ![]() and
and ![]() are orthogonal, then
are orthogonal, then![]() ; else, rewriting
; else, rewriting ![]() as
as ![]() with
with![]() , the component
, the component ![]() of
of ![]() along
along ![]() yields
yields![]() . Thus, according to Equations (3.1),
. Thus, according to Equations (3.1), ![]() , being l the usual notation for the integer quantum number of angular momentum. So
, being l the usual notation for the integer quantum number of angular momentum. So ![]() is effectively a multi-valued quantized function because of the uncertainties initially postulated for
is effectively a multi-valued quantized function because of the uncertainties initially postulated for ![]() and
and![]() . One component of
. One component of ![]() only is actually knowable; the same considerations for the y and x components would trivially mean changing
only is actually knowable; the same considerations for the y and x components would trivially mean changing![]() .
.
Just this conclusion on the physical uniqueness of ![]() suggests that the average values
suggests that the average values![]() ,
, ![]() and
and ![]() should be equal; so the quantity of physical interest to describe the properties of quantum angular momentum is l, as a function of which M2 is now inferred as well. The components averaged over the possible states summing
should be equal; so the quantity of physical interest to describe the properties of quantum angular momentum is l, as a function of which M2 is now inferred as well. The components averaged over the possible states summing ![]() from −L to +L, where L is an arbitrary maximum value of l, yield
from −L to +L, where L is an arbitrary maximum value of l, yield ![]() i.e.
i.e.
![]() (3.3)
(3.3)
Consider the quantum system formed by a particle in a central force field, e.g. an electron around a nuclear charge; the concept of force will be justified in the conceptual frame of (1.12) and (1.11). Assuming the origin O of R on the nucleus, let ![]() be the classical electron energy, where m is the electron mass. As
be the classical electron energy, where m is the electron mass. As![]() , putting again
, putting again ![]() and
and![]() , one finds
, one finds
![]() (3.4)
(3.4)
Two numbers of states, i.e. two quantum numbers, are expected because of the radial and angular uncertainties. In effect the Equations (2.1) and the quantum M2 yield![]() , which reads
, which reads
![]() (3.5)
(3.5)
Minimize ![]() putting
putting![]() , which yields
, which yields
![]() (3.6)
(3.6)
and thus![]() ; so
; so ![]() in order to get
in order to get![]() , i.e. a bound state. The reason of both ways to express
, i.e. a bound state. The reason of both ways to express ![]() will be explained in the section 6. Here are of interest the electron energy levels and rotational energy of the atom as a whole around O
will be explained in the section 6. Here are of interest the electron energy levels and rotational energy of the atom as a whole around O
![]() (3.7)
(3.7)
The physical meaning of ![]() is related to the early Bohr radius, i.e.
is related to the early Bohr radius, i.e. ![]() is due to charges of opposite sign delocalized within a diametric distance
is due to charges of opposite sign delocalized within a diametric distance ![]() apart. So n and l are properties of the phase space, i.e. numbers of allowed quantum states.
apart. So n and l are properties of the phase space, i.e. numbers of allowed quantum states.
Consider now the identity![]() . So it is consequently true that
. So it is consequently true that
![]()
where the last equation of the chain introduces the momentum p by dimensional reasons and reads
![]() (3.8)
(3.8)
It shows the link between De Broglie momentum, Planck energy and condition![]() , according which an integer number of steady electron wavelengths
, according which an integer number of steady electron wavelengths ![]() is defined along a circumference of radius
is defined along a circumference of radius ![]() along which the electron wave propagates at rate v. For such electron waves one finds
along which the electron wave propagates at rate v. For such electron waves one finds
![]() (3.9)
(3.9)
The first chain of equalities will be explained in the next section 6, in particular as concerns the evident link of pc and ![]() with
with![]() . Note here that introducing
. Note here that introducing ![]() to express the quantum energy levels implies defining the De Broglie momentum as a corollary, in agreement with (2.36) and (2.37): appears interesting that the energy levels
to express the quantum energy levels implies defining the De Broglie momentum as a corollary, in agreement with (2.36) and (2.37): appears interesting that the energy levels ![]() of the system are linked to the kinetic energy pc of the electron moving along the circumference of radius
of the system are linked to the kinetic energy pc of the electron moving along the circumference of radius ![]() via the coefficient
via the coefficient![]() . On the one hand, this result emphasizes the electromagnetic character of the interaction between electron and nucleus; comprehensibly
. On the one hand, this result emphasizes the electromagnetic character of the interaction between electron and nucleus; comprehensibly ![]() is proportional to
is proportional to![]() , as the coupling constant determines the force exerted in an interaction, i.e. the greater
, as the coupling constant determines the force exerted in an interaction, i.e. the greater ![]() the smaller
the smaller![]() . On the other hand, it also appears that the key role of the quantum uncertainty in determining the allowed energy levels (3.7) also evidences the kind of interaction itself.
. On the other hand, it also appears that the key role of the quantum uncertainty in determining the allowed energy levels (3.7) also evidences the kind of interaction itself.
These results confirm that the operator formalism and the uncertainty equations are equivalent in describing the quantum systems. As concerns the spin, the paper [6] [7] has shown that it can be inferred without additional hypotheses from the quantization itself. Simply rewriting identically ![]() , one finds
, one finds
![]() (3.10)
(3.10)
after having added ![]() at both sides. Trivial manipulations of the initial
at both sides. Trivial manipulations of the initial ![]() exposed in the quoted paper show that
exposed in the quoted paper show that
![]() (3.11)
(3.11)
and that in general these consideration introduce the spin component![]() ; being of course
; being of course ![]() an arbitrary integer, the quantum uncertainty implies itself the existence of bosons and fermions. No information is necessary about
an arbitrary integer, the quantum uncertainty implies itself the existence of bosons and fermions. No information is necessary about ![]() and
and![]() , which in effect are unknown and unknowable because of the quantum uncertainty.
, which in effect are unknown and unknowable because of the quantum uncertainty.
Besides its inherent worth, the hydrogenlike model has been explicitly quoted here because it also provides useful information about the characteristic lengths in the atom, the first of which is of course the Bohr radius inferred in (3.7). The first powers of ![]() scale further significant lengths starting from this radius, whose essential form reads
scale further significant lengths starting from this radius, whose essential form reads ![]() as a function of the fundamental constants. One infers the following lengths
as a function of the fundamental constants. One infers the following lengths
![]() (3.12)
(3.12)
whose values are
![]()
the Bohr radius scales ![]() down to
down to![]() , electron Compton length, and then to
, electron Compton length, and then to![]() , classical electron radius. Further lengths, shorter and shorter, will be introduced later to extend these definitions and sketch short range nuclear forces. Indeed the fact of having found these well known specific lengths suggests that even the fourth position should reasonably have its own physical meaning at the smaller
, classical electron radius. Further lengths, shorter and shorter, will be introduced later to extend these definitions and sketch short range nuclear forces. Indeed the fact of having found these well known specific lengths suggests that even the fourth position should reasonably have its own physical meaning at the smaller ![]() scale too; if so,
scale too; if so, ![]() can be related to nothing else but the scale of lengths within the atomic nuclei, whose sizes in effect are known to fall between
can be related to nothing else but the scale of lengths within the atomic nuclei, whose sizes in effect are known to fall between ![]() (proton of hydrogen) to
(proton of hydrogen) to ![]() (heavier nuclei).
(heavier nuclei).
3.3. Velocity Dependence of Mass
Owing to (2.28), ![]() reads
reads![]() ; so (2.35) yields
; so (2.35) yields
![]()
This result is more expressively rewritten in the form ![]() fulfilled by
fulfilled by
![]() (3.13)
(3.13)
The physical meaning of this result, the dependence of m on v via the constant![]() , will be clarified soon below. In the following are introduced three interesting ways to implement further the Equations (2.25) and (2.34), to show in particular how results of special relativity are obtainable regarding the local dynamical variables
, will be clarified soon below. In the following are introduced three interesting ways to implement further the Equations (2.25) and (2.34), to show in particular how results of special relativity are obtainable regarding the local dynamical variables ![]() and p as random and unknown values defined in the respective quantum uncertainty ranges
and p as random and unknown values defined in the respective quantum uncertainty ranges ![]() and
and![]() .
.
3.4. Quantum Correction to Special Relativity
The strategy is still that followed to find (2.15) and to infer (2.31) and (2.32) from (2.29). Consider the Equation (2.25) and (2.26) rewritten in the particular case ![]() as
as
![]() (3.14)
(3.14)
the former equation defines the maximum energy range ![]() allowed to the local
allowed to the local ![]() consistently with the given momentum range
consistently with the given momentum range ![]() allowed to any local p. Here energy and momentum ranges are linked each other, whereas in fact they were independent in the Equation (2.28) owing to the arbitrariness of v; so, the upper limit allowed for v implies an upper limit to the size of
allowed to any local p. Here energy and momentum ranges are linked each other, whereas in fact they were independent in the Equation (2.28) owing to the arbitrariness of v; so, the upper limit allowed for v implies an upper limit to the size of ![]() compliant with any possible
compliant with any possible![]() . Anyway this latter is arbitrary; thus both energy and momentum ranges are in fact arbitrary as well, but now correlated. The second position emphasizes the local dynamical variables
. Anyway this latter is arbitrary; thus both energy and momentum ranges are in fact arbitrary as well, but now correlated. The second position emphasizes the local dynamical variables ![]() and p allowed in the respective ranges. The fact that (3.14) is not mere formal way of rewriting (2.25) but contains additional physical information, is easily proven: multiplying side by side both (3.14) one finds
and p allowed in the respective ranges. The fact that (3.14) is not mere formal way of rewriting (2.25) but contains additional physical information, is easily proven: multiplying side by side both (3.14) one finds ![]() i.e., as in (2.14),
i.e., as in (2.14),![]() . So the second (2.34) is instantly inferred via the correlation between
. So the second (2.34) is instantly inferred via the correlation between ![]() and
and ![]() through c.
through c.
However just the fact that the (3.14) appears suitable to be directly linked to (2.34) rises a quantum problem. Replace (2.36) in the Equation (2.34) via the positions ![]() and thus
and thus![]() , being
, being ![]() in fact implied itself by the third (2.36) for
in fact implied itself by the third (2.36) for ![]() too. Then
too. Then ![]() requires
requires![]() . On the one hand nothing hinders in principle to express (2.34) via the corresponding quantum energy and momentum, in agreement with the dual wave/corpuscle character of matter. On the other hand (2.34), as written, seems inadequate to allow both
. On the one hand nothing hinders in principle to express (2.34) via the corresponding quantum energy and momentum, in agreement with the dual wave/corpuscle character of matter. On the other hand (2.34), as written, seems inadequate to allow both ![]() and (2.36). It is reasonable to expect that further terms to be included in (2.34) could overcome this difficulty: the attempt to generalize the standard result of the early special relativity is not only legitimate but also necessary.
and (2.36). It is reasonable to expect that further terms to be included in (2.34) could overcome this difficulty: the attempt to generalize the standard result of the early special relativity is not only legitimate but also necessary.
The subsection 3.2 has been explicitly enclosed in the present exposition to emphasize that the quantum eigenvalues leave out any information about the range sizes; the Equations (3.3) to (3.12) elucidate this assertion. In other words the previous results obtained implementing ![]() could have been identically obtained considering any other
could have been identically obtained considering any other![]() , as the range boundary coordinates are inessential as concerns the quantized eigenvalues of angular momentum and energy. The same holds of course even implementing a linear combination of momentum ranges, e.g.
, as the range boundary coordinates are inessential as concerns the quantized eigenvalues of angular momentum and energy. The same holds of course even implementing a linear combination of momentum ranges, e.g. ![]() via the constant arbitrary coefficients a and b. This means that the local value p defined by
via the constant arbitrary coefficients a and b. This means that the local value p defined by ![]() could be identically replaced by any
could be identically replaced by any ![]() defined by
defined by![]() ; the same holds of course for any
; the same holds of course for any ![]() defined by
defined by ![]() : the only essential requirement is that any range sizes
: the only essential requirement is that any range sizes ![]() and
and ![]() fulfill (3.1), whatever the boundary values might be. Now let us introduce in the relativistic domain this peculiarity of the quantum world. This means that the local values of
fulfill (3.1), whatever the boundary values might be. Now let us introduce in the relativistic domain this peculiarity of the quantum world. This means that the local values of ![]() and
and ![]() defined the respective ranges (3.14) can be replaced by linear combinations of momentum and energy.
defined the respective ranges (3.14) can be replaced by linear combinations of momentum and energy.
The chance of demonstrating the actual effectiveness of this reasoning has heuristic worth in demonstrating the close connection between quantum and relativistic theories.
In practice, to generalize the standard relativistic result (2.34), implement again the first (3.14) with the same steps from (2.29) to (2.31) and then to (2.32), but rewriting the third and fourth positions as
![]()
![]() and
and ![]() are dimensionless arbitrary constants, a and b are arbitrary constants having physical dimensions
are dimensionless arbitrary constants, a and b are arbitrary constants having physical dimensions ![]() and expressing conveniently the
and expressing conveniently the ![]() coefficients. The equations to be implemented are thus
coefficients. The equations to be implemented are thus
![]() (3.15)
(3.15)
where in fact ![]() extend the previous procedure simply introducing additional
extend the previous procedure simply introducing additional ![]() and
and ![]() terms with respect to (3.14) while however keeping a physical meaning still compliant with that of ranges
terms with respect to (3.14) while however keeping a physical meaning still compliant with that of ranges ![]() and
and![]() , as it appears via dimensional considerations. In other words, the second (3.15) still has the usual form
, as it appears via dimensional considerations. In other words, the second (3.15) still has the usual form![]() . Repeat therefore exactly the same procedure just outlined to merge (3.14), i.e. multiply side by side the second and first (3.15) with the a and b terms exchanged of place; omitting for simplicity of notation the asterisk, one finds
. Repeat therefore exactly the same procedure just outlined to merge (3.14), i.e. multiply side by side the second and first (3.15) with the a and b terms exchanged of place; omitting for simplicity of notation the asterisk, one finds
![]() (3.16)
(3.16)
which yields
![]()
and then
![]() (3.17)
(3.17)
Hence, reasoning as before, this result implies:
![]() (3.18)
(3.18)
As hold for (3.18) the same considerations carried out for (2.34), because also the new terms ![]() and
and ![]() vanish for
vanish for![]() . Merging the constants, one finds
. Merging the constants, one finds
![]() (3.19)
(3.19)
The notation ![]() has been kept resulting from the primed constants like in (2.32), in order that this equation reduces to (2.34) in the particular case
has been kept resulting from the primed constants like in (2.32), in order that this equation reduces to (2.34) in the particular case ![]() and
and![]() . Of course the constants
. Of course the constants ![]() and
and ![]() can be included in the respective energies; i.e. with the positions
can be included in the respective energies; i.e. with the positions
![]()
(3,19) reads
![]() (3.20)
(3.20)
As expected, thanks to the higher order terms ![]() and
and ![]() in (3.16) one finds again an equation like the second (2.34) plus two additional terms
in (3.16) one finds again an equation like the second (2.34) plus two additional terms ![]() and
and ![]() not present in the standard special relativity. The quantum correction terms are negligible in (3.20) if
not present in the standard special relativity. The quantum correction terms are negligible in (3.20) if![]() , i.e. if
, i.e. if
![]() (3.21)
(3.21)
then ![]() and
and ![]() fix the scale where the quantum correction plays a significant role. Moreover, if in particular
fix the scale where the quantum correction plays a significant role. Moreover, if in particular![]() , then is effective only the term
, then is effective only the term ![]() in (3.20). These points deserve attention.
in (3.20). These points deserve attention.
First of all, replace ![]() and
and![]() ; being again
; being again![]() , (3.20) reads
, (3.20) reads
![]()
hence (3.20) is compatible with the quantum condition (2.36) even for![]() , whereas
, whereas ![]() is also possible if in particular vanishes the quantity in parenthesis. The last inequality holds for
is also possible if in particular vanishes the quantity in parenthesis. The last inequality holds for![]() , because in general
, because in general![]() , whatever
, whatever ![]() might be.
might be.
Moreover rewrite the second (3.15) with the help of (2.36) as
![]() (3.22)
(3.22)
To recognize the physical meaning of this equation under the condition that ![]() is the constant mass defined by the Equation (3.21), useful positions are:
is the constant mass defined by the Equation (3.21), useful positions are:
![]() (3.23)
(3.23)
The first one is an identity, whose left hand side is simply rewritten introducing the Compton length ![]() of
of![]() . The second one is a formal way to link
. The second one is a formal way to link ![]() and
and ![]() via the parameter r to be defined. The third one regards
via the parameter r to be defined. The third one regards ![]() of (3.22) as an integer multiple of
of (3.22) as an integer multiple of![]() ; in fact the conceptual difference between p defined by (2.23) and
; in fact the conceptual difference between p defined by (2.23) and ![]() is that
is that ![]() is a mere space range that can take in principle any value, the wavelength
is a mere space range that can take in principle any value, the wavelength ![]() requires introducing quantized lengths
requires introducing quantized lengths![]() , which explains why anyway the quantization must be introduced via h in
, which explains why anyway the quantization must be introduced via h in ![]() of (3.1). Although this idea is introduced here as a reasonable input, a previous paper [6] has shown that in effect a huge amount of interesting results is accordingly obtainable. The fourth one will be explained after having replaced the first three (3.23) into (3.22), which reads
of (3.1). Although this idea is introduced here as a reasonable input, a previous paper [6] has shown that in effect a huge amount of interesting results is accordingly obtainable. The fourth one will be explained after having replaced the first three (3.23) into (3.22), which reads
![]() (3.24)
(3.24)
For sake of generality the notation emphasizes that ![]() defining r is not necessarily coincident with n defining the ratio
defining r is not necessarily coincident with n defining the ratio![]() . Is attracting the fourth position (3.23) with
. Is attracting the fourth position (3.23) with ![]() arbitrary integer that expresses the left hand side as
arbitrary integer that expresses the left hand side as ![]() times the harmonic oscillator energy; indeed (3.24) becomes
times the harmonic oscillator energy; indeed (3.24) becomes
![]()
Now it is necessary to express the fact that ![]() is a constant, which in fact means regarding the quantum numbers n and
is a constant, which in fact means regarding the quantum numbers n and ![]() as proportionality factors linking
as proportionality factors linking ![]() and
and![]() . The limit
. The limit ![]() yields
yields ![]() and thus, by comparison with the second and fourth positions (3.23),
and thus, by comparison with the second and fourth positions (3.23),![]() ; so the last equation reads
; so the last equation reads
![]() (3.25)
(3.25)
It appears that if![]() , then
, then ![]() is the energy of harmonic oscillator of frequency
is the energy of harmonic oscillator of frequency![]() . Analogous conclusion holds if
. Analogous conclusion holds if![]() , in which case
, in which case ![]() with
with![]() ; as both n and
; as both n and ![]() are arbitrary integers,
are arbitrary integers, ![]() must be regarded as a new arbitrary integer itself and thus anyone among the numbers already implied by
must be regarded as a new arbitrary integer itself and thus anyone among the numbers already implied by ![]() and
and![]() . So
. So ![]() is an arbitrary multiple of the fundamental frequency
is an arbitrary multiple of the fundamental frequency![]() . The fourth position also allows expressing (3.24) as a function of quantum numbers only
. The fourth position also allows expressing (3.24) as a function of quantum numbers only
![]()
which yields
![]() (3.26)
(3.26)
Next, inserting the positions (3.23) in (3.24) trivial manipulations yield
![]()
Clearly ![]() appearing in (3.24) implied by
appearing in (3.24) implied by ![]() and
and ![]() is different from
is different from ![]() previously found consistent with
previously found consistent with ![]() only; (3.20) skips this restriction.
only; (3.20) skips this restriction.
It is known that (3.20) is a valuable equation of quantum gravity able to solve three cosmological paradoxes [8] . It is hard to guess what has to do the cosmology in this conceptual frame; but in fact this is not the correct way to regard this equation. Rather it is correct to say that the additional terms due to ![]() and
and ![]() add a quantum correction to the standard relativistic formula, actually having quantum character itself being inferred from (2.30) and (2.31); then, once having acknowledged this result, further studies also acknowledge that this correction has valuable cosmological implications as well.
add a quantum correction to the standard relativistic formula, actually having quantum character itself being inferred from (2.30) and (2.31); then, once having acknowledged this result, further studies also acknowledge that this correction has valuable cosmological implications as well.
3.5. Operator Formalism
The subsection 3.2 has shown that the corpuscular approach to quantum mechanics provides sensible results in agreement with the wave formalism. This subsection shows that also the wave formalism enters in the conceptual frame hitherto exposed. Implement the quantum relativistic Equation (3.20), noting that
![]() (3.27)
(3.27)
Admitting that even the single factors at the right hand side have physical meaning, it is possible to introduce imaginary momentum ![]() and energy
and energy ![]() in agreement with the early positions (2.9) and (2.12); the momentum and energy equations take indeed the forms
in agreement with the early positions (2.9) and (2.12); the momentum and energy equations take indeed the forms
![]() (3.28)
(3.28)
being simply required
![]()
The correct correspondence of signs in (3.28) is indeed such that ![]() and thus
and thus![]() , in agreement with (2.17). Whatever the specific form of
, in agreement with (2.17). Whatever the specific form of ![]() might be, replacing p and
might be, replacing p and ![]() of (3.27) with the new definitions (3.28) one finds
of (3.27) with the new definitions (3.28) one finds
![]() (3.29)
(3.29)
in this way the Equation (3.27) turns again into a real form. Introduce now the positions
![]() (3.30)
(3.30)
being
![]() (3.31)
(3.31)
which are justified soon below. In principle the positions (3.30) are compatible each other because ![]() and
and ![]() are arbitrary finite ranges that can be determined in order to fulfill both equations. Note that the more general positions
are arbitrary finite ranges that can be determined in order to fulfill both equations. Note that the more general positions ![]() and
and![]() , with q arbitrary factor, would have been in principle reasonable and possible; however q could be included in m of (3.29), so its specific value is inessential; more important are instead the signs of q, as it will appear shortly. Taking the upper signs (3.30), (3.29) reads as follows
, with q arbitrary factor, would have been in principle reasonable and possible; however q could be included in m of (3.29), so its specific value is inessential; more important are instead the signs of q, as it will appear shortly. Taking the upper signs (3.30), (3.29) reads as follows
![]()
The addend ![]() has been summed and subtracted at the right hand side in order to split this equation as follows
has been summed and subtracted at the right hand side in order to split this equation as follows
![]() (3.32)
(3.32)
the first equation is still the precursor (2.3) of the D’Alembert Equation (2.4) and is clearly an identity ![]() owing to
owing to![]() ; the second equation only involves explicitly m through its reciprocal Compton length. To show why, and how to implement further these equations, note that the first couple of Equations (3.32) merged together yields
; the second equation only involves explicitly m through its reciprocal Compton length. To show why, and how to implement further these equations, note that the first couple of Equations (3.32) merged together yields
![]()
so that one finds
![]() (3.33)
(3.33)
then the position
![]() (3.34)
(3.34)
yields by consequence
![]() (3.35)
(3.35)
Reasonably therefore the positions (3.30) imply (3.32), which yield (3.35) in agreement with (2.35). Hence
![]() (3.36)
(3.36)
It is useful to introduce now the local limit ![]() of the Equations (3.30); once more, the resulting equations take then physical meaning via this limit condition, which introduces an appropriate function
of the Equations (3.30); once more, the resulting equations take then physical meaning via this limit condition, which introduces an appropriate function ![]() defined by the local properties of
defined by the local properties of![]() ; also now indeed the consequent position
; also now indeed the consequent position ![]() turns the Equations (3.30) into the respective differential equations that represent the actual behavior of the particle. So
turns the Equations (3.30) into the respective differential equations that represent the actual behavior of the particle. So
![]() (3.37)
(3.37)
obtained equating the left hand sides of (3.35) and (3.36), are both fulfilled by
![]() (3.38)
(3.38)
being![]() ,
, ![]() and
and ![]() three arbitrary constants. The second equation remarks through the constants
three arbitrary constants. The second equation remarks through the constants ![]() and
and ![]() that the physical dimensions of
that the physical dimensions of ![]() are
are![]() . This equation, which emphasizes the space time range
. This equation, which emphasizes the space time range ![]() already found in (1.7), will be also implemented in the shortened form
already found in (1.7), will be also implemented in the shortened form
![]() (3.39)
(3.39)
An interesting corollary of (3.38) follows from ![]() valid for
valid for![]() . As
. As ![]() , strictly speaking
, strictly speaking ![]() and
and ![]() are linear mass densities in the present one dimensional model; of course in a realistic four dimensional space time C and
are linear mass densities in the present one dimensional model; of course in a realistic four dimensional space time C and ![]() must be intended as usual mass densities, as emphasized in (2.21) and in the next (4.13). Consider
must be intended as usual mass densities, as emphasized in (2.21) and in the next (4.13). Consider ![]() during a fixed time range, so that
during a fixed time range, so that ![]() is regarded as a time constant; then
is regarded as a time constant; then
![]() (3.40)
(3.40)
Although ![]() is dimensionless, appropriate units clarify its physical meaning: multiplying for example both sides by the energy kT already introduced preliminarily in (2.22) but to be defined shortly later, one finds
is dimensionless, appropriate units clarify its physical meaning: multiplying for example both sides by the energy kT already introduced preliminarily in (2.22) but to be defined shortly later, one finds
![]() (3.41)
(3.41)
Hence ![]() is proportional to the chemical potential
is proportional to the chemical potential ![]() an arbitrary space time constant
an arbitrary space time constant ![]() apart.
apart.
Eventually note that ![]() and
and ![]() defined in (3.31) and (3.34) fulfill
defined in (3.31) and (3.34) fulfill![]() ; this equation is also fulfilled putting
; this equation is also fulfilled putting ![]() and
and ![]() with
with ![]() arbitrary factor, in which case it reduces to identity. In particular
arbitrary factor, in which case it reduces to identity. In particular ![]() could be the Lorentz factor, in fact introduced in (2.34); so one infers that
could be the Lorentz factor, in fact introduced in (2.34); so one infers that
![]() (3.42)
(3.42)
is a relativistic invariant in different inertial reference systems. Moreover, dividing both sides by![]() , write the identity
, write the identity
![]() (3.43)
(3.43)
With ![]() equal in particular to the Lorentz factor
equal in particular to the Lorentz factor![]() , as suggested by
, as suggested by ![]() and
and![]() , it is possible to regard the frequency
, it is possible to regard the frequency ![]() as that related to
as that related to ![]() in different inertial reference systems
in different inertial reference systems ![]() and R. Moreover it is also possible to regard
and R. Moreover it is also possible to regard ![]() as the frequency recorded by an observer moving in R at rate v with respect to the frequency
as the frequency recorded by an observer moving in R at rate v with respect to the frequency ![]() emitted by the source. Noting that
emitted by the source. Noting that![]() , let
, let ![]() be such that
be such that ![]() so that
so that![]() . Thus replacing in the second (3.43) one finds
. Thus replacing in the second (3.43) one finds
![]()
This equation is nothing else but the Doppler shift of frequencies reciprocally moving at rate v along their sight line.
As (3.39) shows that both signs of (3.30) are admissible, consider now separately either sign of the Equations (3.36).
1) The negative sign yields
![]() (3.44)
(3.44)
which of course confirm (3.28); so, for ![]() and thus
and thus![]() , the local limits read
, the local limits read
![]() (3.45)
(3.45)
In these equations the physical meaning of ![]() is immediately evident: p is actually a component of the vector p along the x axis on which is defined
is immediately evident: p is actually a component of the vector p along the x axis on which is defined![]() . Instead
. Instead ![]() is more interesting, as it indicates the existence of states of negative energy.
is more interesting, as it indicates the existence of states of negative energy.
Note that holds for (3.44) and (3.45) the same remark carried out for (2.3) and (2.4): also now the left hand side of (3.44) are in fact not calculable explicitly because are indeterminate not only ![]() but also
but also ![]() and
and![]() . However are in principle calculable their limits for
. However are in principle calculable their limits for![]() . Now also the relativistic quantities (3.45) come from and are compliant with the non-real and non-local (3.44). In effect even the Equations (3.45) bring back to the early postulates of the old quantum mechanics, despite obtained from the relativistic (3.27): this is immediately evident via the following positions:
. Now also the relativistic quantities (3.45) come from and are compliant with the non-real and non-local (3.44). In effect even the Equations (3.45) bring back to the early postulates of the old quantum mechanics, despite obtained from the relativistic (3.27): this is immediately evident via the following positions:
![]() (3.46)
(3.46)
In this case ![]() has the same analytical form of
has the same analytical form of![]() . This point deserves further attention.
. This point deserves further attention.
The relativistic equations (3.44) are implied by the invariant xt of (3.39), as shown in (3.42); obviously, replacing xt with another function![]() , the Equation (3.37) would not hold. By consequence, in this case p and
, the Equation (3.37) would not hold. By consequence, in this case p and ![]() in (3.44) would be reasonably replaced by non relativistic quantities
in (3.44) would be reasonably replaced by non relativistic quantities ![]() and
and ![]() numerically different but having however an analogous physical meaning by dimensional reasons: the notation emphasizes the non-relativistic character of their classical approximation. Replace thus
numerically different but having however an analogous physical meaning by dimensional reasons: the notation emphasizes the non-relativistic character of their classical approximation. Replace thus ![]() of
of ![]() in Equation (3.39) with any function
in Equation (3.39) with any function![]() , putting for example
, putting for example![]() : with this Newtonian position where time and space are independent entities defining distinct dynamical variables of classical mechanics, the Equations (3.39) turn respectively into
: with this Newtonian position where time and space are independent entities defining distinct dynamical variables of classical mechanics, the Equations (3.39) turn respectively into
![]()
for simplicity of notation, the symbols of the constants have been kept unchanged. Hence the first two Equations (3.44) turn into
![]()
Put eventually![]() , for example assuming
, for example assuming ![]() proportional to
proportional to![]() ; as c is infinite in classical physics, these equations take the well known form
; as c is infinite in classical physics, these equations take the well known form
![]()
Clearly these expressions, suggested by the outcomes (2.23), agree with (3.28) and specify via the limit ![]() which function is actually involved by the change symbol
which function is actually involved by the change symbol![]() . Hence
. Hence
![]() (3.47)
(3.47)
these results are the well known equations of the old quantum theory; the subscript “ef” stands for “eigenfunction”. The modern quantum physics was born postulating these crucial equations, whence the importance of having found them as corollaries: the present theoretical approach brings back just to early formulation of quantum mechanics and its basic assumptions.
2) Consider now also the plus sign of (3.36), which yields
![]() (3.48)
(3.48)
The Equations (3.64) correspond to the Equations (3.28), whereas the Equations (3.48) read![]() , i.e.
, i.e.![]() ; this expression is a particular case of the Equations (3.1) regarding
; this expression is a particular case of the Equations (3.1) regarding ![]() and
and![]() , where the reference boundaries of these ranges coincide with zero momentum and zero energy. Considering indeed the particular case
, where the reference boundaries of these ranges coincide with zero momentum and zero energy. Considering indeed the particular case ![]() and subtracting side by side one finds again the expected more general result
and subtracting side by side one finds again the expected more general result ![]() in agreement with (3.1) as
in agreement with (3.1) as ![]() and
and![]() . So (3.48) link the operator formalism (3.28) and (3.67) to the uncertainty equations (3.1) and their relativistic implications (3.44).
. So (3.48) link the operator formalism (3.28) and (3.67) to the uncertainty equations (3.1) and their relativistic implications (3.44).
Note eventually that the Equations (3.37) are well known in the operator formalism![]() , where in effect it is taken for granted that
, where in effect it is taken for granted that ![]() ; indeed (3.37) express nothing else but
; indeed (3.37) express nothing else but ![]() previously inferred from (3.30).
previously inferred from (3.30).
In conclusion this simple approach has found the operator formalism and contextually the uncertainty equation, both compatible with relativistic concepts. These outcomes have several further corollaries, the most relevant of which are shortly summarized in the following. Final remark to close this section. The range products ![]() and
and ![]() characterize the quantum uncertainty (3.1), whereas the product
characterize the quantum uncertainty (3.1), whereas the product ![]() characterizes the invariant space time (3.38): the connection between quantum physics and relativistic physics is comprehensible corollary if space and time are mixed in either way. In this respect, what about the other mixed term
characterizes the invariant space time (3.38): the connection between quantum physics and relativistic physics is comprehensible corollary if space and time are mixed in either way. In this respect, what about the other mixed term ![]() also possible in alternative to
also possible in alternative to ![]() of (3.1)? According to (3.1) it yields
of (3.1)? According to (3.1) it yields
![]() (3.49)
(3.49)
the “new” quantity F, so far not explicitly concerned but only anticipated in Section 3.2 for exposition purpose only, takes in this way justification and physical meaning, it is usually known as force. The concept of pressure and energy density also follow from this result dividing both sides by the arbitrary surface ![]()
![]() (3.50)
(3.50)
4. Some Classical Corollaries
Are concerned in this section several interesting outcomes still hidden in the approach hitherto outlined.
4.1. The Fermat and Maupertuis Principles
The key equations are (3.1) and (2.25). Consider an arbitrary time range ![]() during which one particle moves between two coordinates
during which one particle moves between two coordinates ![]() and
and ![]() defining the total path
defining the total path![]() . It is possible to write
. It is possible to write
![]()
the second position expresses that the time interval is arbitrary but fixed by definite time boundaries within which hold the following considerations. Since ![]() traveled by the particle can be imagined as the sum of elementary ranges
traveled by the particle can be imagined as the sum of elementary ranges ![]() corresponding to elementary time steps
corresponding to elementary time steps![]() , write
, write![]() . Being both time and space steps arbitrary, it is possible to replace the sum with an integral and write the following chain of equations with the help of (2.25)
. Being both time and space steps arbitrary, it is possible to replace the sum with an integral and write the following chain of equations with the help of (2.25)
![]()
Hence, integrating along an element ![]() of trajectory for
of trajectory for![]() ,
,
![]()
so the Fermat principle, also expressible identically as ![]() with
with![]() , is actually a straightforward corollary of the uncertainty equation.
, is actually a straightforward corollary of the uncertainty equation.
In an analogous way one finds the Maupertuis principle. Calculate ![]() for
for ![]() and
and ![]() for
for![]() ; in this way, even considering vanishingly small range sizes still holds the concept of local velocity
; in this way, even considering vanishingly small range sizes still holds the concept of local velocity![]() , i.e.
, i.e. ![]() . Considering the coordinates
. Considering the coordinates ![]() and
and ![]() and integrating both sides, one finds according to (3.1)
and integrating both sides, one finds according to (3.1)
![]()
The right hand sides involves ![]() and
and![]() . Suppose now that
. Suppose now that ![]() because
because ![]() is constant itself; then, being
is constant itself; then, being ![]() by definition, one finds
by definition, one finds
![]()
i.e. ![]() and thus
and thus ![]() for any
for any![]() . Hence, along an element
. Hence, along an element ![]() of trajectory,
of trajectory,
![]()
4.2. Further Considerations on the Group Velocity
The reasoning already carried out for a beam of particles, see (2.46), is extended here considering a light beam propagating in a dispersive medium at rate![]() . The Equations (2.37) and (2.36) yield
. The Equations (2.37) and (2.36) yield
![]() (4.1)
(4.1)
of course ![]() of a light wave packet is found through the local limit
of a light wave packet is found through the local limit![]() , i.e.
, i.e.
![]() (4.2)
(4.2)
It is instructive to examine closer the Equation (4.2) in order to evidence that a further aspect of the motion of a corpuscle of mass m is describable by a wave packet moving as a whole with at rate![]() ; the reasoning involves explicitly its energy
; the reasoning involves explicitly its energy ![]() to describe the propagation of the overall shape of the wave packet amplitude through the space. Differentiating the Equation (2.34)
to describe the propagation of the overall shape of the wave packet amplitude through the space. Differentiating the Equation (2.34)
![]()
and replacing ![]() in this equation, trivial calculations yield
in this equation, trivial calculations yield
![]()
Require now purposely![]() , i.e. the wave transports a fixed amount of energy; for example
, i.e. the wave transports a fixed amount of energy; for example ![]() could be just that of one free particle. So
could be just that of one free particle. So
![]() (4.3)
(4.3)
being ![]() the particular value of v fulfilling the given condition; the frequency
the particular value of v fulfilling the given condition; the frequency ![]() is then formally implied by dimensional reasons too. Hence
is then formally implied by dimensional reasons too. Hence
![]()
so that
![]()
then, for ![]() once more,
once more,![]() .
.
The key step of the reasoning is the well defined amount energy ![]() transported at the rate
transported at the rate![]() , by consequence of which results defined the frequency
, by consequence of which results defined the frequency ![]() corresponding to the unique
corresponding to the unique![]() . The different definitions of
. The different definitions of ![]() in (2.36) and in (4.3) are significant; their comparison yields
in (2.36) and in (4.3) are significant; their comparison yields
![]()
Think now one Planck frequency (2.37) as that included in a packet of waves of different wavelengths propagating in a dispersive medium with different λ-dependent velocities: in effect, the Equations (3.1) regard ![]() and
and ![]() as random values within energy and momentum ranges that in turn define various frequencies and momenta corresponding to
as random values within energy and momentum ranges that in turn define various frequencies and momenta corresponding to ![]() and
and![]() . Both statements agree with the fact that the propagation of the particle or its related wave correspond to
. Both statements agree with the fact that the propagation of the particle or its related wave correspond to ![]() and not to the single phase velocities
and not to the single phase velocities![]() . Just for this reason from (3.1) can be inferred the corpuscular and wave aspects of quantum physics.
. Just for this reason from (3.1) can be inferred the corpuscular and wave aspects of quantum physics.
The equations now obtained directly from the Equation (2.34) emphasize a new implication: neither ![]() nor
nor ![]() show explicit reference to the mass, which now becomes mere dimensional parameter inherent the definition of
show explicit reference to the mass, which now becomes mere dimensional parameter inherent the definition of![]() . Appears thus the necessity of explaining how and why the mass is apparently waived from the quantum Equation (2.37) of momentum and energy. In other words, a valid reason is required to replace m with
. Appears thus the necessity of explaining how and why the mass is apparently waived from the quantum Equation (2.37) of momentum and energy. In other words, a valid reason is required to replace m with![]() , being
, being ![]() a new mass even compliant with
a new mass even compliant with ![]() as a limit case. Tentatively this implies defining m as a velocity dependent variable, as in effect it has been already found in the Equation (2.33) and more specifically in (3.13). On the one hand this strategy seems at least in principle adequate to highlight why a moving mass m could turn into an immaterial wave. On the other hand further confirms should be provided next to validate the following way of describing this subtle point.
as a limit case. Tentatively this implies defining m as a velocity dependent variable, as in effect it has been already found in the Equation (2.33) and more specifically in (3.13). On the one hand this strategy seems at least in principle adequate to highlight why a moving mass m could turn into an immaterial wave. On the other hand further confirms should be provided next to validate the following way of describing this subtle point.
4.3. The Refractive Index
According to (3.64) and (2.35), if![]() , then p and
, then p and ![]() are calculable for
are calculable for ![]() only; however even
only; however even ![]() is admissible if contextually
is admissible if contextually![]() . Implementing concurrently both limits, p and
. Implementing concurrently both limits, p and ![]() tend to the indeterminate forms 0/0, which admit in principle finite values. Let
tend to the indeterminate forms 0/0, which admit in principle finite values. Let ![]() and
and ![]() be these limit values, assumed existing by definition: the reverse question rises now, i.e. whether or not
be these limit values, assumed existing by definition: the reverse question rises now, i.e. whether or not ![]() requires
requires![]() . The answer is negative: as the speed of photons in dispersive materials is lower than that in the vacuum, it is possible in principle that photons travel in a dispersive medium at the same v allowed to a beam of massive particles. The fact that
. The answer is negative: as the speed of photons in dispersive materials is lower than that in the vacuum, it is possible in principle that photons travel in a dispersive medium at the same v allowed to a beam of massive particles. The fact that ![]() is compatible with both
is compatible with both ![]() and
and![]() , suggests that the kinetic mass m should actually be function of v itself: if so, then the separate correspondences
, suggests that the kinetic mass m should actually be function of v itself: if so, then the separate correspondences ![]() and
and ![]() merge into the unique correspondence
merge into the unique correspondence ![]() provided that an appropriate function of
provided that an appropriate function of ![]() does exist. In other words it should be true that both
does exist. In other words it should be true that both ![]() and
and ![]() are compatible with a unique
are compatible with a unique ![]() via
via![]() . In fact this conclusion has been already inferred in (2.33), where the concept of mass was introduced in the present model as rest mass. The following reasoning represents the extension of this concept to the kinetic mass.
. In fact this conclusion has been already inferred in (2.33), where the concept of mass was introduced in the present model as rest mass. The following reasoning represents the extension of this concept to the kinetic mass.
Regard m of (2.33) as a particular case of a general dynamical variable related to p through v and examine how the new concept of mass could tend to zero correspondingly to![]() ; is interesting in this respect the position
; is interesting in this respect the position
![]() (4.4)
(4.4)
which regards m as a constant mass while introducing a new mass![]() . The Equation (2.33) has anticipated this conclusion in the particular case where
. The Equation (2.33) has anticipated this conclusion in the particular case where ![]() for
for![]() , whereas a further hint to the concept of rest mass has been provided by (3.13). Replacing formally m of (4.4) in both (3.64) one obtains
, whereas a further hint to the concept of rest mass has been provided by (3.13). Replacing formally m of (4.4) in both (3.64) one obtains ![]() while contextually
while contextually![]() ; then, eliminating
; then, eliminating ![]() from these results, one still finds
from these results, one still finds ![]() in agreement with (2.34). So
in agreement with (2.34). So ![]() fulfills the same relativistic formula of p with initial mass m, despite now the limit for
fulfills the same relativistic formula of p with initial mass m, despite now the limit for ![]() corresponds to the finite value
corresponds to the finite value ![]() implemented in (3.14) and (3.15); this relationship between energy and momentum is expected in general for a wave, see Equation (2.24). Hold for
implemented in (3.14) and (3.15); this relationship between energy and momentum is expected in general for a wave, see Equation (2.24). Hold for ![]() all steps from (3.14) to (3.20). The wavelike implication of (4.4) is further acknowledged considering
all steps from (3.14) to (3.20). The wavelike implication of (4.4) is further acknowledged considering ![]() of (2.14).
of (2.14).
In conclusion, according to the quantum uncertainty the behavior of a corpuscle of mass m should inherently have a wave-like propagation too, whereas the fact that ![]() for
for ![]() shows that m and
shows that m and ![]() are rest and kinetic masses. So the Equation (4.4) in fact generalizes the concepts of m and
are rest and kinetic masses. So the Equation (4.4) in fact generalizes the concepts of m and ![]() introduced in (2.33):
introduced in (2.33): ![]() is the particular value pertinent to m at the specific speed v. As a consequence note that
is the particular value pertinent to m at the specific speed v. As a consequence note that ![]() define a pure number
define a pure number
![]() (4.5)
(4.5)
that introduces the refractive index of the medium where propagates an electromagnetic wave at velocity![]() ; owing to the Equation (6.2) in fact
; owing to the Equation (6.2) in fact![]() , as it has been already introduced in (2.46) and (4.1). Moreover the position (4.4) also agrees with (2.45); indeed
, as it has been already introduced in (2.46) and (4.1). Moreover the position (4.4) also agrees with (2.45); indeed
![]()
takes into account that ![]() depends on the refractive index of the medium through which propagates the electromagnetic wave or the De Broglie pilot wave. The position (4.4) introduces thus the first step to explain how and why the concept of mass does not explicitly appear in (2.45): once having introduced the refraction index, v is in fact eliminated from the equations being replaced by n. Formally this means expressing the displacement rate v of the particle in c units; yet v appears subsequently also as the rate
depends on the refractive index of the medium through which propagates the electromagnetic wave or the De Broglie pilot wave. The position (4.4) introduces thus the first step to explain how and why the concept of mass does not explicitly appear in (2.45): once having introduced the refraction index, v is in fact eliminated from the equations being replaced by n. Formally this means expressing the displacement rate v of the particle in c units; yet v appears subsequently also as the rate ![]() at which a single wave phase propagates. This fact encourages thinking that somehow it should be possible to infer a formula that specifically emphasizes what the Equations (3.64) and (2.45) already show themselves, i.e. the way m and
at which a single wave phase propagates. This fact encourages thinking that somehow it should be possible to infer a formula that specifically emphasizes what the Equations (3.64) and (2.45) already show themselves, i.e. the way m and ![]() replace each other in defining p and
replace each other in defining p and![]() . The mathematical approach to this task proceeds noting that
. The mathematical approach to this task proceeds noting that
![]() (4.6)
(4.6)
so that the right hand side represents kinetic energy. On the one hand ![]() corresponds to the classical mass defining the kinetic energy, although for
corresponds to the classical mass defining the kinetic energy, although for ![]() the deviation of
the deviation of ![]() from m is irrelevant for practical purposes. On the other hand it is possible to write
from m is irrelevant for practical purposes. On the other hand it is possible to write
![]() (4.7)
(4.7)
The second equation is direct consequence of the first one; it emphasizes that the concerned velocity v is actually ![]() of (2.45), because in general this latter and not v of (2.3) is related to and describable by n. This confirms that
of (2.45), because in general this latter and not v of (2.3) is related to and describable by n. This confirms that ![]() is the effective value of m when the particle velocity takes up just the specific value
is the effective value of m when the particle velocity takes up just the specific value ![]() pertinent to the group velocity at which propagates the wave packet. As expected
pertinent to the group velocity at which propagates the wave packet. As expected ![]() for
for![]() , whereas
, whereas ![]() for
for![]() ; in effect according to (3.13)
; in effect according to (3.13) ![]() is definable even for
is definable even for![]() , so (2.33) and (4.4) are compliant with these limits. Regard thus the addends of (4.7) as probabilities, whose sum represents the certainty of concerning the existing particle through its mass displacement velocity or wave propagation rate. The first addend describes the probability for the particle to loose its classical kinetic mass, till to become an immaterial propagation wave; the second addend, previously introduced to express the actual velocity
, so (2.33) and (4.4) are compliant with these limits. Regard thus the addends of (4.7) as probabilities, whose sum represents the certainty of concerning the existing particle through its mass displacement velocity or wave propagation rate. The first addend describes the probability for the particle to loose its classical kinetic mass, till to become an immaterial propagation wave; the second addend, previously introduced to express the actual velocity ![]() of the particle, takes the meaning of reciprocal refraction index n of the resulting wave, being it in effect still related to the propagation rate of the wave/particle. The addends account therefore for the dual behavior of matter in a probabilistic way correspondingly to the probability of energy fluctuation, thanks to which the particle effectively displaces with velocity dependent mass or with frequency dependent propagation rate of a wave packet: indeed, one must also expect an appropriate energy fluctuation to balance the chances of mass energy loss. Obviously to this mass change correspond different p and
of the particle, takes the meaning of reciprocal refraction index n of the resulting wave, being it in effect still related to the propagation rate of the wave/particle. The addends account therefore for the dual behavior of matter in a probabilistic way correspondingly to the probability of energy fluctuation, thanks to which the particle effectively displaces with velocity dependent mass or with frequency dependent propagation rate of a wave packet: indeed, one must also expect an appropriate energy fluctuation to balance the chances of mass energy loss. Obviously to this mass change correspond different p and ![]() and thus different
and thus different![]() , whence the necessity of linking m with a group of waves that spread with collective
, whence the necessity of linking m with a group of waves that spread with collective ![]() given by (2.45). So the worth of (4.7) is that of having emphasized the quantum probabilistic meaning of the relativistic position (4.6).
given by (2.45). So the worth of (4.7) is that of having emphasized the quantum probabilistic meaning of the relativistic position (4.6).
These considerations rise however three questions.
The first one can be formulated as follows: as (4.7) is made by mass and massless terms, what determines either property of matter? Obviously the immediate answer points to the kind of experiment made on the particles constituting the body of matter. Also this is the non-real essence of quantum mechanics, which actually regards the matter neither as a packet of waves nor as a cluster of corpuscles, but as an undefined state of probabilistic mixing of both states until some experiment “creates” either state. The electron diffraction in the two slit experiment and the Thomson experiment inspired by the Millikan result elucidate the physical meaning of the addends of (4.7). To this equation is also related the physical meaning of the EPR thought paradox, showing that the quantum properties are not pre-definable outcomes according to some principles of classical mechanics, rather they are created by the experiment itself. In effect (3.1) exclude not only the concept of trajectory, but also that of distance and velocity; as shown in 3.2 the local space time coordinates must be replaced by the respective ranges, so concepts like “superluminal” distance are actually unphysical. In this sense the EPR paradox shouldn’t even be formulated: replacing systematically ![]() and
and ![]() are missing the concepts themselves of point to point space distance and time to time lapse needed to define any “superluminal” effect; remember that in effect according to (2.8) and (2.9)
are missing the concepts themselves of point to point space distance and time to time lapse needed to define any “superluminal” effect; remember that in effect according to (2.8) and (2.9) ![]() is introduced “as such”, i.e. as a fundamental constant of Nature regardless the ratio
is introduced “as such”, i.e. as a fundamental constant of Nature regardless the ratio ![]() over
over![]() .
.
The second one concerns the addition of velocities. Consider an electromagnetic wave that appears in the point where![]() . An example is the annihilation of m by collision with its antiparticle purposely assumed in the vacuum: one would naively expect that the new born electromagnetic wave should propagate at rate classically resulting from its own velocity c summed up to that v initially characterizing the moving center of mass of the annihilating particles. Yet (2.48) has already negatively answered this question.
. An example is the annihilation of m by collision with its antiparticle purposely assumed in the vacuum: one would naively expect that the new born electromagnetic wave should propagate at rate classically resulting from its own velocity c summed up to that v initially characterizing the moving center of mass of the annihilating particles. Yet (2.48) has already negatively answered this question.
The third question concerns the energy fluctuation necessary to account for the mass change when![]() . This point is concerned in the next two subsections.
. This point is concerned in the next two subsections.
4.4. Energy Fluctuation
The corpuscle/wave dualism has been accepted as compelling experimental evidence since the early experiments of electron diffraction, simply acknowledging that either behavior depends on the kind of experiment. Yet this shortcut leaves in fact unexplained why mass appears explicitly in (3.64) whereas it is hidden in the proportionality constants (2.36), despite both concern momentum and energy of a free particle. The fact that both equations have been inferred in the frame of a unique model based on the definitions (1.11) and (1.12) stimulates one to think that even this duality could find rational explanation, i.e. explainable by a logical physical reasoning in the conceptual frame of the present model, without need of supplementary “ad hoc” hypotheses. This hope is supported by the probabilistic character of (4.7), direct consequence of the concept of velocity dependent mass elucidated in the form (4.4): in effect the chances ![]() and
and ![]() or respectively
or respectively ![]() and
and ![]() appear in principle reciprocally consistent and compliant with the unity, i.e. the certainty that anyway something travels through the space time as amount of mass or wave: in the former case it is appropriate to think about corpuscle displacement velocity, in the latter about wave propagation rate. The validity of this idea is proposed in this subsection not only by evidencing its self-consistency, but also quoting as a verification further well known results contextually obtainable.
appear in principle reciprocally consistent and compliant with the unity, i.e. the certainty that anyway something travels through the space time as amount of mass or wave: in the former case it is appropriate to think about corpuscle displacement velocity, in the latter about wave propagation rate. The validity of this idea is proposed in this subsection not only by evidencing its self-consistency, but also quoting as a verification further well known results contextually obtainable.
The results of the point 4.3 have been obtained considering initially a particle of mass m that displaces at rate v; next has been considered also its probability of mass, i.e. energy, fluctuation, which eventually turns it into massless electromagnetic wave or matter wave traveling at rates ![]() or
or ![]() respectively. On the one hand, besides the formal similarity with the propagation of either kind of wave, the Equations (4.5) and (4.4) show that this virtual process scales both p and
respectively. On the one hand, besides the formal similarity with the propagation of either kind of wave, the Equations (4.5) and (4.4) show that this virtual process scales both p and ![]() to
to ![]() and
and ![]() by a common factor related to the refractive index. On the other hand, this also implies an energy change that occurs in a time range
by a common factor related to the refractive index. On the other hand, this also implies an energy change that occurs in a time range![]() , being
, being ![]() the arbitrary time at which the mass m starts modifying its value.
the arbitrary time at which the mass m starts modifying its value.
Owing to (2.34), consider thus the energy change ![]() since when the particle starts loosing its initial mass m to when eventually
since when the particle starts loosing its initial mass m to when eventually ![]() according to (4.7). The fluctuation driven energy change is summarized by the following equations
according to (4.7). The fluctuation driven energy change is summarized by the following equations
![]() (4.8)
(4.8)
The energy range ![]() must not be confused with
must not be confused with ![]() of (3.1):
of (3.1): ![]() concerns the quantum uncertainty unavoidably constraining the arbitrary variability range allowed to the conjugate dynamical variables of any system,
concerns the quantum uncertainty unavoidably constraining the arbitrary variability range allowed to the conjugate dynamical variables of any system, ![]() is instead the specific energy fluctuation allowed in particular to the particle during the mass loss virtual process that “converts” it into a wave. The time length related to
is instead the specific energy fluctuation allowed in particular to the particle during the mass loss virtual process that “converts” it into a wave. The time length related to ![]() is thus
is thus
![]() (4.9)
(4.9)
The Equation (4.9) yields
![]() (4.10)
(4.10)
these positions are easily understood; the respective energies proportional to ![]() and
and ![]() are also proportional to the frequencies
are also proportional to the frequencies ![]() and
and![]() . Of course the only way to regard this result in the wave formalism of quantum mechanics is the link between frequencies and energies, which in fact is just the Planck position: precisely in this sense the probabilistic Equation (4.7) introduces the ratio
. Of course the only way to regard this result in the wave formalism of quantum mechanics is the link between frequencies and energies, which in fact is just the Planck position: precisely in this sense the probabilistic Equation (4.7) introduces the ratio![]() , mass addend, and the corresponding ratio
, mass addend, and the corresponding ratio![]() , wave addend. This confirms that the corpuscle/wave behavior has probabilistic origin and follows an energy fluctuation of quantum matter.
, wave addend. This confirms that the corpuscle/wave behavior has probabilistic origin and follows an energy fluctuation of quantum matter.
Are the Equation (4.8) along with its premises and implications true indeed? To support the validity of (4.7) and thus (4.8) itself, is now tested their direct consequence, the Equation (4.9), in three particular cases of major physical interest. Write first with the help of (3.1) and (2.25)
![]() (4.11)
(4.11)
noting that ![]() has physical dimensions of diffusion coefficient D introduced in (2.19); this suggests that
has physical dimensions of diffusion coefficient D introduced in (2.19); this suggests that![]() , being
, being ![]() an appropriate proportionality coefficient to be determined. So
an appropriate proportionality coefficient to be determined. So
![]() (4.12)
(4.12)
The coefficient ![]() is crucial to specify the kind of problem precisely concerned.
is crucial to specify the kind of problem precisely concerned.
1) Putting first ![]() means describing one particle that displaces with diffusion coefficient D through
means describing one particle that displaces with diffusion coefficient D through ![]() at average velocity v. Strictly speaking, as previously remarked about the Equation (3.60), in the present one space dimensional model (3.39) defines C as linear density
at average velocity v. Strictly speaking, as previously remarked about the Equation (3.60), in the present one space dimensional model (3.39) defines C as linear density ![]() instead of the actual
instead of the actual![]() ; yet C regarded in the usual 3-dimensional space allows to define the actual physical dimensions of flux J of matter, i.e.
; yet C regarded in the usual 3-dimensional space allows to define the actual physical dimensions of flux J of matter, i.e.![]() . Multiplying both sides of the first equality
. Multiplying both sides of the first equality ![]() by
by![]() , being C mass per unit volume, yields
, being C mass per unit volume, yields![]() . This result is more appropriately rewritten as
. This result is more appropriately rewritten as![]() ; the double sign accounts for the fact that v is actually a velocity component on the x-axis along which is defined
; the double sign accounts for the fact that v is actually a velocity component on the x-axis along which is defined![]() , correspondingly to the definition
, correspondingly to the definition ![]() of the Equation (2.19). Simple dimensional considerations allow defining the equation
of the Equation (2.19). Simple dimensional considerations allow defining the equation
![]() (4.13)
(4.13)
that introduces with the minus sign the concept of mass flux J, i.e. mass transferred per unit surface and time through the volume V; so ![]() is due to the diffusion driven matter transfer between the surfaces
is due to the diffusion driven matter transfer between the surfaces ![]() apart of an ideal cube of matter of volume V. The Equation (4.13) completes the Equations (2.19), as it is well known. Anyway, merging both expressions (4.13) of J, one finds
apart of an ideal cube of matter of volume V. The Equation (4.13) completes the Equations (2.19), as it is well known. Anyway, merging both expressions (4.13) of J, one finds![]() ; then, recalling (3.60) and (3.61) as already done in (2.22), the limit
; then, recalling (3.60) and (3.61) as already done in (2.22), the limit ![]() yields
yields
![]() (4.14)
(4.14)
The double sign of v is obvious, being it a velocity component. For simplicity and brevity v and D have been regarded not dependent on x, to make quickly recognizable the link of these results with well known concepts of elementary diffusion theory; also, the diffusion process has been assumed at the constant temperature T. With the minus sign in (4.13), positive D, one acknowledges once more the definition of chemical potential ![]() in agreement with (3.61). Moreover, as the
in agreement with (3.61). Moreover, as the ![]() is equivalent to a force
is equivalent to a force![]() , this yields also the famous Einstein-Smoluchowski relationship between mobility
, this yields also the famous Einstein-Smoluchowski relationship between mobility ![]() and diffusion coefficient D, i.e.
and diffusion coefficient D, i.e.
![]() (4.15)
(4.15)
Eventually the plus sign in (4.13), which instead corresponds to negative D, describes phenomena like the spinodal decomposition of alloys of appropriate composition [9] .
2) Putting next ![]() and writing thus (4.12) as
and writing thus (4.12) as ![]() means describing one particle that travels with diffusion coefficient D the distance
means describing one particle that travels with diffusion coefficient D the distance ![]() at average velocity
at average velocity![]() . The factor 1/2 specifies therefore that the particle displaces around the mean coordinate
. The factor 1/2 specifies therefore that the particle displaces around the mean coordinate ![]() towards both sides of
towards both sides of![]() , in which case
, in which case ![]() at the right hand side of (4.11) reads
at the right hand side of (4.11) reads ![]() and takes thus the statistical meaning of average square displacement
and takes thus the statistical meaning of average square displacement ![]() of the particle traveling through the whole range around
of the particle traveling through the whole range around![]() . So the second equality (4.12) yields
. So the second equality (4.12) yields
![]() (4.16)
(4.16)
i.e. the famous Einstein equation of one dimensional Brownian motion.
3) The validity of the Equation (4.8) is further checked implementing the property![]() . Consider now a system of particles, the i-th of which has energy
. Consider now a system of particles, the i-th of which has energy![]() . The fact that
. The fact that ![]() is in general
is in general ![]() times greater than
times greater than ![]() suggests the possible chance of regarding the former as
suggests the possible chance of regarding the former as ![]() and the latter as the sum of an appropriate number N of terms
and the latter as the sum of an appropriate number N of terms ![]() such that
such that![]() ; clearly N depends of the value of
; clearly N depends of the value of ![]() and size of all ranges
and size of all ranges![]() . Anyway the initial Equation (4.8) is compatible with the position
. Anyway the initial Equation (4.8) is compatible with the position
![]() (4.17)
(4.17)
simply requiring
![]()
as in principle n can take any value from 1 to ∞, the number of terms of the sum is arbitrary. The Equation (4.17) is well known and reported in all standard textbooks concerning the fluctuations of thermodynamic systems: it yields ![]() and thus
and thus ![]() regarding appropriately
regarding appropriately ![]() and
and ![]() as average quantities. So with
as average quantities. So with ![]() and
and![]() , follows then immediately
, follows then immediately
![]() (4.18)
(4.18)
4.5. Liouville Theorem
An interesting question concerning (3.1) is the following: is ![]() simply an energy range or is it even compatible with the physical meaning of difference between two diverse forms
simply an energy range or is it even compatible with the physical meaning of difference between two diverse forms ![]() and
and ![]() of energy? This question, which according to (2.25) involves
of energy? This question, which according to (2.25) involves ![]() too, is answered rewriting identically (3.1) as
too, is answered rewriting identically (3.1) as
![]() (4.19)
(4.19)
The first equality reads
![]() (4.20)
(4.20)
the second equality reads
![]() (4.21)
(4.21)
Now fulfill the idea that ![]() defines the difference of two distinct energies, specifically T and U introduced in section 2.3, which implies the chance of writing in general
defines the difference of two distinct energies, specifically T and U introduced in section 2.3, which implies the chance of writing in general![]() . To highlight this point, concerning in particular the energies already introduced in (2.41) and (2.42), introduce the following positions
. To highlight this point, concerning in particular the energies already introduced in (2.41) and (2.42), introduce the following positions
![]() (4.22)
(4.22)
in this way the sign of ![]() in (4.20) is uniquely defined since T only depends on
in (4.20) is uniquely defined since T only depends on![]() , whereas is expected the double sign in (4.21) because both energies T and U depend on x. As in effect
, whereas is expected the double sign in (4.21) because both energies T and U depend on x. As in effect ![]() is the component of
is the component of ![]() along the x-axis, so that it can actually take in principle both signs, rewrite explicitly (4.21) as
along the x-axis, so that it can actually take in principle both signs, rewrite explicitly (4.21) as
![]() (4.23)
(4.23)
the double sign on the one hand emphasizes that both p and ![]() are actually components of the vectors
are actually components of the vectors ![]() and
and ![]() along the x-axis. The last two equations also agree with the fact that in principle
along the x-axis. The last two equations also agree with the fact that in principle
![]()
in lack of any information about the ranges, both inequalities are actually possible. Regarded in this way, i.e. implementing range boundaries arbitrary and independent each other, the notation (4.23) effectively defines ![]() as difference of two energies reasonably dissimilar according to (4.22). Taking the ratios side by side of the first Eqs (4.20) and (4.21) one finds
as difference of two energies reasonably dissimilar according to (4.22). Taking the ratios side by side of the first Eqs (4.20) and (4.21) one finds
![]() (4.24)
(4.24)
It is immediate to link (4.24) and (4.22), noting that the former defines at both sides ratios with physical dimensions of reciprocal time range. Multiplying both sides by![]() , the equations
, the equations
![]() (4.25)
(4.25)
define energies that, in agreement with (2.42) and (2.38), correspond respectively to
![]()
Hence simple considerations on the range boundaries imply the concepts of Hamiltonian and Lagrangian according to the previous Equations (2.38) and (2.42): ![]() has been identified with the Lagrangian of a particle, H with the Hamiltonian of the system. In particular, is of interest here
has been identified with the Lagrangian of a particle, H with the Hamiltonian of the system. In particular, is of interest here
![]()
for the following reason. According to the quantum uncertainty, the left hand side of (3.1) reads![]() , where the number of scalars, so far intuitively associated to the three usual space dimensions only, is actually arbitrary, i.e. extensible to any number j of extra-dimensions required by some theories or, alternatively, to the number of freedom degrees allowed to the system of particles: in fact any freedom degree has its pertinent
, where the number of scalars, so far intuitively associated to the three usual space dimensions only, is actually arbitrary, i.e. extensible to any number j of extra-dimensions required by some theories or, alternatively, to the number of freedom degrees allowed to the system of particles: in fact any freedom degree has its pertinent ![]() and
and![]() . Thus it is sensible to introduce the dimensionless quantity
. Thus it is sensible to introduce the dimensionless quantity ![]() where fall all points in the multidimensional phase space defined by the sizes of all
where fall all points in the multidimensional phase space defined by the sizes of all ![]() and
and ![]() of the corresponding particles with respect to
of the corresponding particles with respect to![]() . Accordingly
. Accordingly
![]()
yields
![]()
the range ![]() includes all points of coordinates x and p falling within
includes all points of coordinates x and p falling within ![]() elementary cells of j-dimensional volume
elementary cells of j-dimensional volume ![]() in the phase space. So
in the phase space. So
![]()
yields then
![]()
according to the first (4.25)![]() , i.e. the volume
, i.e. the volume ![]() along phase space trajectories where
along phase space trajectories where![]() .
.
5. Some Thermodynamic Corollaries
The last results have somehow linked the relativistic Equation (2.25) to important results of classical statistical thermodynamics. The importance of this topic is shortly highlighted in the following three subsections.
5.1. Statistical Sets of Particles
Let us implement once more the Equation (2.26), and calculate the change of ![]() according to the following chain of equations
according to the following chain of equations
![]()
Since by definition
![]()
being ![]() and
and ![]() arbitrary constants, it is possible to write
arbitrary constants, it is possible to write
![]()
Consider now preliminarily the case of an ideal gas of non-interacting free particles/atoms/ions/molecules and let ![]() and
and ![]() the momenta and energies of each particle. Then, owing to the last equality, it is possible to write for each i-th particle
the momenta and energies of each particle. Then, owing to the last equality, it is possible to write for each i-th particle
![]()
moreover it is also possible to sum terms like this of each particle over all particles of the system, so that it is possible to write
![]()
whence
![]() (5.1)
(5.1)
being N the number of particles of the system. Note that this result is actually more general than prospected here. Suppose first two interacting particles only; in this case we expect ![]() and
and ![]() for the first particle and
for the first particle and ![]() and
and ![]() for the second one because of their interaction: despite the first (2.34) holds for a free particle, it is reasonable to think that changing appropriately
for the second one because of their interaction: despite the first (2.34) holds for a free particle, it is reasonable to think that changing appropriately ![]() and
and ![]() one can describe at least approximately even an interacting particle. For example it is possible to replace
one can describe at least approximately even an interacting particle. For example it is possible to replace ![]() with
with![]() , being
, being ![]() an appropriate correction factor. Anyway,
an appropriate correction factor. Anyway, ![]() and
and ![]() are in principle calculable; summing these terms, the left hand side of (5.1) involves
are in principle calculable; summing these terms, the left hand side of (5.1) involves![]() . In the case of three particles mutually interacting one would obtain
. In the case of three particles mutually interacting one would obtain ![]() defining
defining![]() , and so on for any number of particles all mutually interacting. On the one hand this means that now the previous
, and so on for any number of particles all mutually interacting. On the one hand this means that now the previous ![]() is replaced by
is replaced by![]() , whereas the summation is possibly extended to a different number of terms. On the other hand this reasoning holds also for
, whereas the summation is possibly extended to a different number of terms. On the other hand this reasoning holds also for ![]() and also for multiple primed probabilities. In fact, summing all
and also for multiple primed probabilities. In fact, summing all ![]() or all
or all ![]() does not change the conceptual statistical meaning of the sum; in other words, whatever
does not change the conceptual statistical meaning of the sum; in other words, whatever ![]() might be, one could include appropriate correction factors to the various
might be, one could include appropriate correction factors to the various ![]() of the allowed states; normalizing the sums, one still obtains an equation like (5.1). To calculate how each
of the allowed states; normalizing the sums, one still obtains an equation like (5.1). To calculate how each ![]() turns into
turns into ![]() and next into
and next into ![]() because of these interactions, is in general difficult and must be examined case by case; yet, if we content ourselves to describe the evolution of the system as a whole from the non-interacting to the interacting state, the form of the final equation is still similar to the previous (5.1) obtained for free particles. Omitting for simplicity the primed or multiple primed notations for
because of these interactions, is in general difficult and must be examined case by case; yet, if we content ourselves to describe the evolution of the system as a whole from the non-interacting to the interacting state, the form of the final equation is still similar to the previous (5.1) obtained for free particles. Omitting for simplicity the primed or multiple primed notations for ![]() and
and ![]() in the following, introduce the positions
in the following, introduce the positions
![]() (5.2)
(5.2)
where ![]() is now a proportionality constant. The factor N in (5.2) simply shows that S is an extensive property. Introduce the condition expressed by the equivalent positions
is now a proportionality constant. The factor N in (5.2) simply shows that S is an extensive property. Introduce the condition expressed by the equivalent positions
![]() (5.3)
(5.3)
where ![]() can be 0 or more in general
can be 0 or more in general ![]() in this one dimensional model where
in this one dimensional model where ![]() is actually a component of
is actually a component of ![]() that can take both signs. The first condition regards a completely disordered system of particles regarded as a whole at the equilibrium, whose velocities are randomly distributed both by modulus and direction with equal probability. The second condition assumes a macroscopic system in an unstable situation out of equilibrium, e.g. gas with an internal pressure gradient due to a non uniform distribution of velocities; this can happen for example for a system of charged particles in an inhomogeneous external field. Whatever its particle velocity distribution might be, both chances are assumed compatible with the third position (5.2).
that can take both signs. The first condition regards a completely disordered system of particles regarded as a whole at the equilibrium, whose velocities are randomly distributed both by modulus and direction with equal probability. The second condition assumes a macroscopic system in an unstable situation out of equilibrium, e.g. gas with an internal pressure gradient due to a non uniform distribution of velocities; this can happen for example for a system of charged particles in an inhomogeneous external field. Whatever its particle velocity distribution might be, both chances are assumed compatible with the third position (5.2).
Actually nothing compels these positions, which in effect are purposely introduced to plug the present considerations into the realm of statistical mechanics. In practice ![]() shows that the equilibrium corresponds to the maximum possible disorder of the system as concerns the velocity distribution of its constituting particles. This statement, assumed valid in general and not in the present one dimensional case only, can be regarded as boundary condition of (5.2) as it implies
shows that the equilibrium corresponds to the maximum possible disorder of the system as concerns the velocity distribution of its constituting particles. This statement, assumed valid in general and not in the present one dimensional case only, can be regarded as boundary condition of (5.2) as it implies![]() , in this particular case
, in this particular case![]() . According to (5.2) this constant can be nothing else but the right hand side, i.e.
. According to (5.2) this constant can be nothing else but the right hand side, i.e.
![]() (5.4)
(5.4)
This is nothing else but the Boltzmann definition of dimensionless entropy: note that ![]() constant indeed does not mean that it has one fixed value only, but that it does not depend on the index of summation states I, whereas it depends of course on T.
constant indeed does not mean that it has one fixed value only, but that it does not depend on the index of summation states I, whereas it depends of course on T.
This simple procedure has introduced the function S as sum of consistent functions ![]() of all particles of the system; the summation over i has been extended to the velocities
of all particles of the system; the summation over i has been extended to the velocities ![]() of all particles of the system. This summation is surely positive and finite because all
of all particles of the system. This summation is surely positive and finite because all![]() .
.
It is possible to ask at this point whether this kind of equation is uniquely referable to the property![]() , or it has a more general worth, e.g. in the case of probability distribution function of states such that
, or it has a more general worth, e.g. in the case of probability distribution function of states such that![]() . This expectation is sensible, being a particular case of the second (5.3). The next subsection concerns just this point.
. This expectation is sensible, being a particular case of the second (5.3). The next subsection concerns just this point.
5.2. The Entropy
The starting point is now (3.38) with the minus sign. The way to implement this equation is similar to that just described for the Equation (5.1): any space time factor ![]() is regarded as
is regarded as![]() , with notation that goes back to the section 1 in order to specify an arbitrary j-th state of a system of particles at the time
, with notation that goes back to the section 1 in order to specify an arbitrary j-th state of a system of particles at the time![]() . The system defined in this way is a statistical set in the sense previously highlighted for each
. The system defined in this way is a statistical set in the sense previously highlighted for each![]() , in agreement with the definition of
, in agreement with the definition of![]() : in other words, the variation of configuration of the system implies reasonably the change of local space coordinates of a cluster of j-th particles enclosed in
: in other words, the variation of configuration of the system implies reasonably the change of local space coordinates of a cluster of j-th particles enclosed in ![]() during the time range
during the time range![]() : both ranges define a possible state in the phase space as described in the subsection 4.5. Actually both
: both ranges define a possible state in the phase space as described in the subsection 4.5. Actually both ![]() and
and ![]() were inherent the definition of
were inherent the definition of ![]() in subsection 5.1; similarly W must be be introduced here in order to describe the non-instantaneous evolution of a local small volume of the system during space time ranges that represent its configuration change rate. The Equations (3.60) and (3.61) show that this way of thinking allowed to infer the chemical potential
in subsection 5.1; similarly W must be be introduced here in order to describe the non-instantaneous evolution of a local small volume of the system during space time ranges that represent its configuration change rate. The Equations (3.60) and (3.61) show that this way of thinking allowed to infer the chemical potential ![]() hidden in
hidden in![]() ; let us examine here the possibility of extracting further thermodynamic information from this function.
; let us examine here the possibility of extracting further thermodynamic information from this function.
The algebraic steps are listed one by one after rewriting (3.38) as
![]() (5.5)
(5.5)
1) On the basis of the section 5.1, define
![]() (5.6)
(5.6)
being ![]() positive factor dependent on the time
positive factor dependent on the time ![]() only;
only;
2) regard![]() , i.e. any local space time coordinate xt is defined as one that characterizes the j-th state of each particle in the space range
, i.e. any local space time coordinate xt is defined as one that characterizes the j-th state of each particle in the space range ![]() during the time range
during the time range![]() , which implies
, which implies ![]() while
while ![]() and
and ![]() as well
as well
![]() (5.7)
(5.7)
3) sum over all allowed states j accessible during an assigned ![]() by all particles in the phase space
by all particles in the phase space
![]() (5.8)
(5.8)
whereas the factor ![]() is defined by
is defined by
![]() (5.9)
(5.9)
4) the last Equation (5.9) defines a “new” quantity T called temperature
![]() (5.10)
(5.10)
uniquely defined for a body of matter at the thermal equilibrium. Note that the first equation has been written introducing at the left hand side the summation over ![]() only. Also note that
only. Also note that
![]()
i.e.
![]() (5.11)
(5.11)
the j-th addend contributing to ![]() is to be considered to calculate the right hand side. Multiplying both sides by
is to be considered to calculate the right hand side. Multiplying both sides by ![]() one finds
one finds
![]()
and then, summing over j, owing to (5.8) one finds
![]() (5.12)
(5.12)
Normalizing via![]() , this result reads
, this result reads
![]() (5.13)
(5.13)
If ![]() this equation emphasizes the certainty resulting from the sum of two positive terms, which therefore can be regarded as probabilities. If
this equation emphasizes the certainty resulting from the sum of two positive terms, which therefore can be regarded as probabilities. If ![]() measures the disorder of the system, then reasonably
measures the disorder of the system, then reasonably ![]() measures the order: the sum of these probabilities yields the certainty that both order and disorder concur to define the state of any system. In other words, any system can be partially ordered and partially disordered; e.g. some parts of a crystal lattice can contain in general local point and/or line pile up defects inside a surrounding defect free volume.
measures the order: the sum of these probabilities yields the certainty that both order and disorder concur to define the state of any system. In other words, any system can be partially ordered and partially disordered; e.g. some parts of a crystal lattice can contain in general local point and/or line pile up defects inside a surrounding defect free volume.
This probabilistic interpretation is possible if![]() : in other words, the probability of modifying the local order/disorder of the system requires according to (5.12)
: in other words, the probability of modifying the local order/disorder of the system requires according to (5.12) ![]() inside any
inside any ![]() at different
at different ![]() at which is calculated
at which is calculated![]() . Let be therefore
. Let be therefore ![]() and
and ![]() the changes allowed to occur within any space range
the changes allowed to occur within any space range ![]() at any time within
at any time within ![]() and rewrite W of (5.5) according to the positions (5.7) via (3.1) and (2.28); once more the space ranges, and not the local space time coordinates they represent, are physically appropriate to describe the changes in the system. Replacing
and rewrite W of (5.5) according to the positions (5.7) via (3.1) and (2.28); once more the space ranges, and not the local space time coordinates they represent, are physically appropriate to describe the changes in the system. Replacing ![]() and
and ![]() one finds
one finds
![]()
having expressed ![]() according to the current notation; clearly
according to the current notation; clearly ![]() is the pertinent energy change corresponding to the configuration change in progress within
is the pertinent energy change corresponding to the configuration change in progress within![]() . Hence, keeping
. Hence, keeping ![]() and
and ![]() constants, write
constants, write
![]()
and thus
![]() .
.
In this way ![]() and
and ![]() describe the changes occurring in
describe the changes occurring in ![]() with respect to
with respect to ![]() in the given region
in the given region ![]() of the system. Certainly the local
of the system. Certainly the local ![]() is due to the corresponding local changes of
is due to the corresponding local changes of ![]() and
and![]() ; however it is in principle possible that even at
; however it is in principle possible that even at ![]() both these latter remain still included in the same range size
both these latter remain still included in the same range size ![]() where they were at
where they were at![]() ; this simply means that
; this simply means that ![]() is small enough to imply correspondingly small changes of
is small enough to imply correspondingly small changes of ![]() and
and ![]() that therefore still remain included within the same
that therefore still remain included within the same![]() . While acknowledging that this is in principle admissible because all range sizes are in principle arbitrary, it is interesting to compare what happens at
. While acknowledging that this is in principle admissible because all range sizes are in principle arbitrary, it is interesting to compare what happens at ![]() and
and![]() . If for example
. If for example ![]() by definition, i.e. the former is greater than the latter because it must include increasing values of local time coordinates
by definition, i.e. the former is greater than the latter because it must include increasing values of local time coordinates![]() , then
, then ![]() implies
implies![]() . The negative sign of
. The negative sign of ![]() means that on the one hand
means that on the one hand ![]() fulfils via
fulfils via ![]() the probabilistic meaning of (5.13) and that on the other hand it also implies all
the probabilistic meaning of (5.13) and that on the other hand it also implies all![]() . Thus summing over j all terms
. Thus summing over j all terms ![]() at all
at all ![]() one infers
one infers
![]() . (5.14)
. (5.14)
Clearly this is just the second law of thermodynamics because, as written, it concerns an isolated system; the conclusion is in effect true if no external action perturbs the system. If not so, then any action altering substantially the configuration of the system modifies by consequence the j-th range size too; in general different ![]() and
and ![]() are reasonablyimplied before and after the external action. Thus, in particular, it can result that
are reasonablyimplied before and after the external action. Thus, in particular, it can result that ![]() while however (5.13) can be again fulfilled:
while however (5.13) can be again fulfilled: ![]() still holds even with
still holds even with ![]() but
but![]() . Clearly in the system no longer isolate the external action has modified the spontaneous tendency towards increasing entropy.
. Clearly in the system no longer isolate the external action has modified the spontaneous tendency towards increasing entropy.
It is worth remarking once more that the evolution of the physical system has implemented two subsequent time lapses ![]() and
and![]() , not two deterministic time coordinates
, not two deterministic time coordinates ![]() and
and![]() : these latter and the respective deterministic
: these latter and the respective deterministic ![]() and
and ![]() representing the external action would be incompatible with the Heisenberg principle.
representing the external action would be incompatible with the Heisenberg principle.
5.3. The Statistical Distributions
Let the change ![]() of W be
of W be![]() , being w an arbitrary amount added or subtracted to the initial value of W. On the one hand W can increase or decrease by any physical reason with respect to its initial value; the double sign indicates that no reason is guessable to expect that the change consists of either increase only or decrease only of the initial value W. On the other hand it is also reasonable to expect that
, being w an arbitrary amount added or subtracted to the initial value of W. On the one hand W can increase or decrease by any physical reason with respect to its initial value; the double sign indicates that no reason is guessable to expect that the change consists of either increase only or decrease only of the initial value W. On the other hand it is also reasonable to expect that![]() , being q an arbitrary proportionality factor and
, being q an arbitrary proportionality factor and ![]() an arbitrary value allowed to W consistent with (5.5); this position means that anyway the change
an arbitrary value allowed to W consistent with (5.5); this position means that anyway the change ![]() implies a new quantity still related to the meaning of thermodynamic probability
implies a new quantity still related to the meaning of thermodynamic probability ![]() coherent with W. In other words,
coherent with W. In other words, ![]() is such that
is such that ![]() and
and ![]() are respectively compatible and physically consistent with
are respectively compatible and physically consistent with![]() . The fact that both
. The fact that both ![]() and
and ![]() must fulfill (5.8) likewise the initial W, allows expecting the consistency of the following considerations with the equations up to (5.10) as well. If so, then
must fulfill (5.8) likewise the initial W, allows expecting the consistency of the following considerations with the equations up to (5.10) as well. If so, then
![]() (5.15)
(5.15)
yields
![]() (5.16)
(5.16)
put in this form, once more the space time Equation (5.5) of W is implemented via ![]() and related
and related![]() , similarly to the position (5.8) leading to the results (5.10). The Equation (5.15) has been written in order to emphasize how w is to be regarded in agreement with either sign, i.e.
, similarly to the position (5.8) leading to the results (5.10). The Equation (5.15) has been written in order to emphasize how w is to be regarded in agreement with either sign, i.e. ![]() and
and![]() . In conclusion, recalling the Equation (5.5),
. In conclusion, recalling the Equation (5.5),
![]()
also here appears the space time function![]() . Hence, according to the reasoning to infer the Equation (4.14) via (3.60) and (3.61), at any given time
. Hence, according to the reasoning to infer the Equation (4.14) via (3.60) and (3.61), at any given time ![]() and thus
and thus![]() . In conclusion
. In conclusion
![]() (5.17)
(5.17)
This equation follows from the arbitrariness of![]() , consistent with that of
, consistent with that of![]() ; the multiplicative factor
; the multiplicative factor ![]() has simply included
has simply included ![]() in the constant addend of chemical potential
in the constant addend of chemical potential ![]() together with
together with![]() . Implement now either
. Implement now either
![]()
of (5.15): being ![]() by definition, there is no constrain to the number
by definition, there is no constrain to the number ![]() related to the negative sign in the Equation (5.17), whereas the positive sign of this equation requires
related to the negative sign in the Equation (5.17), whereas the positive sign of this equation requires ![]() i.e.
i.e.![]() . This constrain suggests the possible physical meaning of
. This constrain suggests the possible physical meaning of ![]() in (5.17). Let
in (5.17). Let ![]() be the numbers of states with a given energy
be the numbers of states with a given energy![]() , i.e. the degeneracy of the state, and
, i.e. the degeneracy of the state, and ![]() the number of particles in the given state; if so, then it is easy to realize that in the latter case
the number of particles in the given state; if so, then it is easy to realize that in the latter case ![]() can take only the values 0 and 1 whatever
can take only the values 0 and 1 whatever ![]() might be [10] . All details published elsewhere are omitted here for sake of brevity. Thus (5.17) is the well known formula of statistical distribution of fermions and bosons with degeneracy
might be [10] . All details published elsewhere are omitted here for sake of brevity. Thus (5.17) is the well known formula of statistical distribution of fermions and bosons with degeneracy![]() .
.
5.4. The Phase Space
Entropy and Liouville theorem, both previously inferred, are the key concepts to introduce the phase space. As this topic is well known, are reported here just a few remarks aimed only to emphasize the link between space time and phase space; i.e. the concept of space time is actually the third essential ingredient to introduce “ab initio” the statistical mechanics. To this purpose consider in particular the Equations (3.39) and (3.1).
Being x and t arbitrary and independent variables, which represent for example the space coordinate of a given particle at various times in the space time, any value of xt can be obtained keeping constant either factor and allowing appropriate values of the other one; both ways of defining an arbitrary space time coordinate ![]() are numerically and conceptually equivalent to describe each one among N particles of the system at given time
are numerically and conceptually equivalent to describe each one among N particles of the system at given time ![]() in the range of space coordinates
in the range of space coordinates ![]() or at
or at ![]() during the time range
during the time range![]() . According to (3.1), indeed, the space time coordinate of each particle is defined within allowed variability ranges
. According to (3.1), indeed, the space time coordinate of each particle is defined within allowed variability ranges ![]() and
and![]() . So is physically significant the amount
. So is physically significant the amount![]() , whatever these range sizes might be. To highlight this point consider the following equations obtained implementing (3.1) and (2.28)
, whatever these range sizes might be. To highlight this point consider the following equations obtained implementing (3.1) and (2.28)
![]()
whence
![]()
and thus, comparing the initial and final ranges of coordinates,
![]() (5.18)
(5.18)
the initial equation regards the j-th space coordinate ![]() at the time
at the time![]() , the former defined within the interval
, the former defined within the interval ![]() the latter in the time range
the latter in the time range![]() ; the final equation rewrites the first one with exchanged indexes j and k. As in effect the first two equations are summarized in the third one, it means that the concerned particle is described at different times
; the final equation rewrites the first one with exchanged indexes j and k. As in effect the first two equations are summarized in the third one, it means that the concerned particle is described at different times ![]() and
and ![]() by different space ranges
by different space ranges ![]() and
and![]() , to which correspond the respective momenta
, to which correspond the respective momenta ![]() and
and![]() ; moreover it also follows
; moreover it also follows![]() , as it must be because anyway the Equation (3.1) must be fulfilled no matter how any particle moves in the space time. In other words, as j and k are not specified or specifiable, the particle moves actually through any random space and time ranges in the phase space according to its position and momentum of the space time. This can be better evidenced and generalized rewriting with trivial manipulations the last equation
, as it must be because anyway the Equation (3.1) must be fulfilled no matter how any particle moves in the space time. In other words, as j and k are not specified or specifiable, the particle moves actually through any random space and time ranges in the phase space according to its position and momentum of the space time. This can be better evidenced and generalized rewriting with trivial manipulations the last equation
![]() (5.19)
(5.19)
i.e. one particle initially at any random ![]() within
within ![]() at the random time
at the random time ![]() included in
included in ![]() is actually found within another
is actually found within another ![]() at the subsequent time
at the subsequent time ![]() within time range
within time range![]() . Obviously this chain could be further extended starting again from the last term
. Obviously this chain could be further extended starting again from the last term![]() , which in effect has the same form of the first one but is simply rewritten with different subscripts; the first and last terms of this chain represent different space time coordinates and thus its ability of the particle to fill various coordinate and momentum ranges defining the whole phase space. All accessible local coordinates of space time correspond to the respective local coordinates of space phase, with equal probability.
, which in effect has the same form of the first one but is simply rewritten with different subscripts; the first and last terms of this chain represent different space time coordinates and thus its ability of the particle to fill various coordinate and momentum ranges defining the whole phase space. All accessible local coordinates of space time correspond to the respective local coordinates of space phase, with equal probability.
5.5. Further Comments about the Diffusion Coefficient
The diffusion coefficient D introduced in (2.19) is usually concerned in problems of matter displacement under non-equilibrium conditions, essentially due to concentration gradients; the same holds for the heat diffusion coefficient (2.22) in non-thermal equilibrium problems, typically in the presence of temperature gradients. However, the four equations from (4.13) to (4.16), as well as the next (5.20) and (5.21), suggest a more profound physical meaning of D. In this respect deserve attention the following three remarks.
1) The dimensional definition of D is![]() ; this yields
; this yields![]() , i.e.
, i.e.![]() , being of course
, being of course ![]() and
and ![]() arbitrary constants. Then, reasoning likewise in (4.14), the right hand side yields
arbitrary constants. Then, reasoning likewise in (4.14), the right hand side yields![]() , being C the amount of mass in a given volume V. Hence, being
, being C the amount of mass in a given volume V. Hence, being![]() , as found in (3.60) and (3.61), one finds
, as found in (3.60) and (3.61), one finds ![]() and therefore
and therefore
![]() (5.20)
(5.20)
this is the usual form to express the dependence of diffusion coefficient on temperature via the activation energy ![]() and the reference constant
and the reference constant![]() .
.
2) Assume now a body of matter of mass m in equilibrium at temperature T and implement the reasonable idea that both D and ![]() take finite ranges of allowed values. Let
take finite ranges of allowed values. Let ![]() and
and ![]() be the respective limit values of interest here; is then significant the particular case where the Equation (4.15) concerns the minimum temperature
be the respective limit values of interest here; is then significant the particular case where the Equation (4.15) concerns the minimum temperature ![]() defined as follows
defined as follows
![]() (5.21)
(5.21)
Dimensional considerations are useful to guess an order of magnitude estimate of![]() . The reciprocal mobility
. The reciprocal mobility ![]() has physical dimensions
has physical dimensions![]() , whereas D is
, whereas D is![]() ; so their product represents the minimum energy
; so their product represents the minimum energy![]() . The notation emphasizes that the energy of interest to calculate
. The notation emphasizes that the energy of interest to calculate ![]() excludes the contribution of thermal vibrations, being instead due to the mere confinement of a particle or a body of matter within a finite delocalization range
excludes the contribution of thermal vibrations, being instead due to the mere confinement of a particle or a body of matter within a finite delocalization range![]() ; accordingly, it is sensible to define
; accordingly, it is sensible to define ![]() as
as![]() . In fact the Equations (3.1) justify the existence of this form of energy and related force.
. In fact the Equations (3.1) justify the existence of this form of energy and related force.
Consider indeed one particle of mass m ideally delocalized between two infinite potential walls ![]() apart; in a one dimensional model it is possible to write
apart; in a one dimensional model it is possible to write
![]() (5.22)
(5.22)
having expressed ![]() via an appropriate proportionality constant
via an appropriate proportionality constant![]() . This result is understandable thinking an oscillating particle confined in
. This result is understandable thinking an oscillating particle confined in![]() , so that m bounces back and forth between the potential walls with frequency
, so that m bounces back and forth between the potential walls with frequency![]() . In fact
. In fact ![]() is the time lapse to complete one oscillation cycle;
is the time lapse to complete one oscillation cycle; ![]() is the range defined by the maximum delocalization momentum
is the range defined by the maximum delocalization momentum ![]() related to the range size and
related to the range size and ![]() when the particle inverts its motion on both potential walls. This picture agrees with
when the particle inverts its motion on both potential walls. This picture agrees with![]() , i.e. with the physical impossibility of conceiving a localized particle at rest and thus with
, i.e. with the physical impossibility of conceiving a localized particle at rest and thus with ![]() in fixed point exactly defined. The circular frequency here introduced is justifiable from a more realistic three dimensional point of view, where the back and forth one dimensional motion of m reads actually
in fixed point exactly defined. The circular frequency here introduced is justifiable from a more realistic three dimensional point of view, where the back and forth one dimensional motion of m reads actually ![]() and thus
and thus![]() ; i.e. m describes a closed circular path at tangential velocity
; i.e. m describes a closed circular path at tangential velocity ![]() inside its confinement delocalization volume V, so far not yet introduced explicitly. In effect it is also possible to evidence the confinement volume writing
inside its confinement delocalization volume V, so far not yet introduced explicitly. In effect it is also possible to evidence the confinement volume writing
![]() (5.23)
(5.23)
Anyway it is sensible that![]() , being presumably a fixed value, cannot depend on the arbitrary m and specific
, being presumably a fixed value, cannot depend on the arbitrary m and specific![]() ; rather
; rather ![]() is to be regarded as a universal property of matter uniquely defined. Both requirements suggest restarting from the relativistic energy equation
is to be regarded as a universal property of matter uniquely defined. Both requirements suggest restarting from the relativistic energy equation ![]() of one free particle of arbitrary mass m, which however must no longer appear explicitly. Implementing thus the wave expression of momentum
of one free particle of arbitrary mass m, which however must no longer appear explicitly. Implementing thus the wave expression of momentum![]() , which in fact allows introducing the expected oscillation behavior as that related to the concept of wavelength
, which in fact allows introducing the expected oscillation behavior as that related to the concept of wavelength![]() , one finds
, one finds
![]() (5.24)
(5.24)
which thus also defines
![]()
The 3D generalization of this result is obtained imagining an arbitrary amount of mass delocalized in an appropriate range![]() , regarded as the diametric size of a hypersphere of radius
, regarded as the diametric size of a hypersphere of radius ![]() to which is related the maximum value of
to which is related the maximum value of![]() : the idea is to implement steady matter waves of wavelengths
: the idea is to implement steady matter waves of wavelengths ![]() propagating through the hypersphere at rate
propagating through the hypersphere at rate![]() . Regard thus an arbitrary mass of an isolate free corpuscle ideally bouncing within one diametric distance, whose extent corresponds to one half wavelength; the largest zero point wavelength is that with steady nodes on the opposite boundaries of the hypersphere diameter and is thus
. Regard thus an arbitrary mass of an isolate free corpuscle ideally bouncing within one diametric distance, whose extent corresponds to one half wavelength; the largest zero point wavelength is that with steady nodes on the opposite boundaries of the hypersphere diameter and is thus![]() . This implies that
. This implies that ![]() defined by the zero point momentum wavelength
defined by the zero point momentum wavelength ![]() corresponds to back and forth delocalization through twice the diametric size
corresponds to back and forth delocalization through twice the diametric size ![]() of the hypersphere: this is the physical meaning of (5.22) where
of the hypersphere: this is the physical meaning of (5.22) where ![]() whence
whence![]() . Also, imagining asymptotically
. Also, imagining asymptotically ![]() to simulate
to simulate ![]() and recalling (5.22), it is possible to conclude
and recalling (5.22), it is possible to conclude
![]() (5.25)
(5.25)
These results will be calculated later; regardless of the numerical values, however, it is possible to remark since now some interesting implications:
− The Nernst theorem is automatically fulfilled, i.e. the absolute zero actually does not exist being clearly impossible to remove the zero point energy, which is an intrinsic feature itself of any amount of confined matter.
− As expected, the related zero point temperature ![]() does not depend on the specific amount and physical nature of m.
does not depend on the specific amount and physical nature of m.
− Is in principle possible the quantization of temperature, which accordingly should start from ![]() and change by discrete steps of the order of
and change by discrete steps of the order of ![]() itself.
itself.
3) The reasoning to infer (5.21) and (5.25) introduces![]() , whose physical meaning is relevant: it implies that
, whose physical meaning is relevant: it implies that ![]() is somehow linked to the possible granular structure of the space time.
is somehow linked to the possible granular structure of the space time.
To show this last point, calculate the change ![]() of the space time coordinates around any local coordinate
of the space time coordinates around any local coordinate ![]() and
and![]() . The result is elucidated by the following chains of equations implementing once more the Equations (3.1):
. The result is elucidated by the following chains of equations implementing once more the Equations (3.1):
![]()
since the expression at right hand side reads
![]()
with notation of (6.4), then
![]()
It is possible to identify here a minimum value of ![]() defined by
defined by ![]() and
and![]() , at least asymptotically. Anyway one finds
, at least asymptotically. Anyway one finds
![]() (5.26)
(5.26)
Whatever the specific value of ![]() might be, is interesting the conceptual idea of “granular” space time determined by a minimum linear size of cells, in the present one-dimensional model
might be, is interesting the conceptual idea of “granular” space time determined by a minimum linear size of cells, in the present one-dimensional model![]() , that define any macroscopic values of xt within these cell; the third (5.26) corresponds to the definition of invariant interval, which is known to be the basis of the special relativity [11] .
, that define any macroscopic values of xt within these cell; the third (5.26) corresponds to the definition of invariant interval, which is known to be the basis of the special relativity [11] .
Accordingly, the Lorentz transformations, in particular, should actually be nothing else but the straightforward consequence of the granular nature of space time.
5.6. Further Comments about the Zero Point Energy
This section generalizes the idea of regarding the zero point energy and volume (5.23) as intrinsic properties of matter, rather than as operative thermodynamic parameters related to specific experimental conditions. According to (5.23), think the zero point volume ![]() considering for example an atom surrounded by neighbor lattice atoms;
considering for example an atom surrounded by neighbor lattice atoms; ![]() corresponds to its free lattice volume, whatever it might be depending on temperature and mobility. The fact that
corresponds to its free lattice volume, whatever it might be depending on temperature and mobility. The fact that ![]() is defined by the confinement lattice volume around a given atom/ion, implies the limit
is defined by the confinement lattice volume around a given atom/ion, implies the limit ![]() simply because for an isolated free particle
simply because for an isolated free particle![]() . Nonetheless
. Nonetheless ![]() depends itself on T, both because of the thermal dilation of matter that modifies the size of lattice spacing and because the T dependent mobility allows one lattice atom to spread well beyond its volume at
depends itself on T, both because of the thermal dilation of matter that modifies the size of lattice spacing and because the T dependent mobility allows one lattice atom to spread well beyond its volume at ![]() via the so called “self-diffusion” [12] . Moreover
via the so called “self-diffusion” [12] . Moreover ![]() also depends on the presence of lattice defects, which affect the free space available for its delocalization. In particular, one expects that the lattice atom is quenched in one lattice site at
also depends on the presence of lattice defects, which affect the free space available for its delocalization. In particular, one expects that the lattice atom is quenched in one lattice site at ![]() only; in other words the volume V is a thermodynamic parameter experimentally set, whereas
only; in other words the volume V is a thermodynamic parameter experimentally set, whereas ![]() is determined by the physics of matter. In the absence of external fields at
is determined by the physics of matter. In the absence of external fields at![]() , therefore,
, therefore, ![]() is the minimum non-thermal energy of the lattice atom/ion, as it results from all possible interactions with lattice neighbors that determine the available free confinement volume; at
is the minimum non-thermal energy of the lattice atom/ion, as it results from all possible interactions with lattice neighbors that determine the available free confinement volume; at![]() , the thermal energy kT represents actually the additional contribution to the non-thermal zero point energy
, the thermal energy kT represents actually the additional contribution to the non-thermal zero point energy![]() , so that it seems reasonable to think that in general the simple kT should be implemented as
, so that it seems reasonable to think that in general the simple kT should be implemented as![]() . This holds in particular for the FD and BE statistical distributions. In the case of a single free particle this does not hold, as its delocalization volume is infinity by definition: but in general, when considering the thermodynamic properties of a body of matter,
. This holds in particular for the FD and BE statistical distributions. In the case of a single free particle this does not hold, as its delocalization volume is infinity by definition: but in general, when considering the thermodynamic properties of a body of matter, ![]() cannot be longer omitted at least in principle.
cannot be longer omitted at least in principle.
To justify the legitimacy of this conclusion, consider first an ideal gas inside which energy exchanges occur via direct collisions between its molecules only. Without hypothesizing specific interactions between molecules, e.g. long range Coulomb or dipole interactions between electron shells, holds between p and ![]() of each molecule the general equation
of each molecule the general equation
![]() (5.27)
(5.27)
the second equality introduces the time lapse ![]() between any successive shocks, during which the molecule travels freely the distance
between any successive shocks, during which the molecule travels freely the distance![]() . During each
. During each ![]() therefore
therefore ![]() remains constant, since inside the gas the energy changes are supposedly due to direct collisions only. In particular, as concerns the zero point energy,
remains constant, since inside the gas the energy changes are supposedly due to direct collisions only. In particular, as concerns the zero point energy,
![]()
the notation is justified by the free volume ![]() dependence analogous to that of the Equation (P77). The fact that
dependence analogous to that of the Equation (P77). The fact that ![]() involves
involves ![]() is not surprising;
is not surprising; ![]() comes from
comes from ![]() in (5.27) and agrees with
in (5.27) and agrees with![]() , being
, being ![]() the total range of momentum change
the total range of momentum change ![]() after one shock between molecules.
after one shock between molecules.
Let ![]() be the distance between one molecule just after its last shock and the wall of the recipient containing the gas; in general
be the distance between one molecule just after its last shock and the wall of the recipient containing the gas; in general![]() . Moreover, as
. Moreover, as![]() , (5.27) yields
, (5.27) yields
![]() (5.28)
(5.28)
where ![]() is the impact force of the concerned molecule against the wall. If A is the surface of the wall, then the pressure due to the shock of one molecule is
is the impact force of the concerned molecule against the wall. If A is the surface of the wall, then the pressure due to the shock of one molecule is
![]() (5.29)
(5.29)
If ![]() is such that
is such that![]() , then the former equation becomes
, then the former equation becomes![]() ; so, since the numerator has physical dimensions
; so, since the numerator has physical dimensions![]() , the result reads
, the result reads
![]() (5.30)
(5.30)
Note that in general neither ![]() nor
nor ![]() are necessarily constants independent of time; so the pressure
are necessarily constants independent of time; so the pressure ![]() inferred in (5.30) could be variable during subsequent time lapses
inferred in (5.30) could be variable during subsequent time lapses![]() . Also note that to infer this result in the present one dimensional model it is enough to think the plane A orthogonal to the space coordinate
. Also note that to infer this result in the present one dimensional model it is enough to think the plane A orthogonal to the space coordinate![]() . In a general three dimensional approach one should integrate over all possible incidence angles of the molecule against the wall to obtain the pressure, as it is well known. This would entail a numerical factor, which however can be included in
. In a general three dimensional approach one should integrate over all possible incidence angles of the molecule against the wall to obtain the pressure, as it is well known. This would entail a numerical factor, which however can be included in ![]() and thus is irrelevant for the present purposes. Moreover, it is still possible to define a statistical value of
and thus is irrelevant for the present purposes. Moreover, it is still possible to define a statistical value of ![]() averaging the shocks over several time lapses during a time range
averaging the shocks over several time lapses during a time range![]() . So is defined the quantum pressure
. So is defined the quantum pressure
![]()
This result has been obtained considering the delocalization volume of one molecule; it holds in general for any number N of molecules regarding ![]() no longer as volume of a single molecule but as total experimental volume
no longer as volume of a single molecule but as total experimental volume ![]() of ideal gas simply with the position
of ideal gas simply with the position![]() . The right hand side is the average confinement size of the molecule. It is significant to conclude that the pressure of the gas must be expressed not only taking into account the variable dynamical parameter
. The right hand side is the average confinement size of the molecule. It is significant to conclude that the pressure of the gas must be expressed not only taking into account the variable dynamical parameter ![]() experimentally determined but adding to this latter the contribution
experimentally determined but adding to this latter the contribution ![]() having merely quantum nature; in effect the present reasoning waives considerations about any state equation of ideal or real gases. Also, regarding the macroscopic volume
having merely quantum nature; in effect the present reasoning waives considerations about any state equation of ideal or real gases. Also, regarding the macroscopic volume ![]() as a further dynamical parameter experimentally set, it contains the quantum contribution
as a further dynamical parameter experimentally set, it contains the quantum contribution![]() . So, extending the reasoning carried out for one gas molecule to the case of N molecules, one finds
. So, extending the reasoning carried out for one gas molecule to the case of N molecules, one finds
![]() (5.31)
(5.31)
The volume ![]() is easily understandable, being intuitively evident that the molecules have finite size contributing to the total volume
is easily understandable, being intuitively evident that the molecules have finite size contributing to the total volume ![]() experimentally measurable. Even
experimentally measurable. Even ![]() is guessable: if the zero point energy is simulated by an oscillator characterized by a non-thermal vibrational frequency that determines the zero point energy, see the next Equation (5.22), then the energy of any oscillator in the gas volume defines a confinement non-thermal energy density equivalent to pressure, see next Equations (8.34). Indeed (5.31) shows that even at
is guessable: if the zero point energy is simulated by an oscillator characterized by a non-thermal vibrational frequency that determines the zero point energy, see the next Equation (5.22), then the energy of any oscillator in the gas volume defines a confinement non-thermal energy density equivalent to pressure, see next Equations (8.34). Indeed (5.31) shows that even at![]() , e.g. the core of a free body of matter in the vacuum with zero applied pressure, there is a residual internal pressure, non-eliminable, e.g. it could act substantially similarly to the repulsion between electron shells of molecules; moreover the latter equation shows even a non-reducible residual volume
, e.g. the core of a free body of matter in the vacuum with zero applied pressure, there is a residual internal pressure, non-eliminable, e.g. it could act substantially similarly to the repulsion between electron shells of molecules; moreover the latter equation shows even a non-reducible residual volume![]() . The relationship between energy, pressure and volume follows directly from (5.29) as
. The relationship between energy, pressure and volume follows directly from (5.29) as ![]() at fixed temperature: indeed at the right hand side of the first equality appear fixed quantities, of course at given
at fixed temperature: indeed at the right hand side of the first equality appear fixed quantities, of course at given ![]() and
and ![]() and thus constant T. So
and thus constant T. So
![]()
This equation reminds closely the characteristic terms of the Van der Waals equation, where f and ![]() are approximately regarded as gas constants; this holds also here, even though the pressure and volume terms (5.31) have been inferred considering initially an ideal gas via quantum considerations about its constituting molecules. The interactions between these molecules, even not hypothesized and purposely introduced “a priori”, appear as quantum effects regardless of specific considerations about their actual nature, which is in effect “hidden” in parameters like
are approximately regarded as gas constants; this holds also here, even though the pressure and volume terms (5.31) have been inferred considering initially an ideal gas via quantum considerations about its constituting molecules. The interactions between these molecules, even not hypothesized and purposely introduced “a priori”, appear as quantum effects regardless of specific considerations about their actual nature, which is in effect “hidden” in parameters like ![]() or
or ![]() or f descriptive of the properties of the gas; hence is not surprising that the coefficients
or f descriptive of the properties of the gas; hence is not surprising that the coefficients ![]() and
and ![]() contribute to that characterizing the famous Van der Waals equation. The conceptual reasons underlying this equation are well known; is interesting however that the form of the resulting equation based on the present approach is analogous to that just found.
contribute to that characterizing the famous Van der Waals equation. The conceptual reasons underlying this equation are well known; is interesting however that the form of the resulting equation based on the present approach is analogous to that just found.
These considerations are now extended to the concept of temperature once having introduced the quantum meaning of ![]() related to
related to ![]() to show that the zero point energy, typical quantum effect, affects the macroscopic properties of gases: ideal gas is the one where these quantum effects are approximately neglected along with the long range mutual interactions as well.
to show that the zero point energy, typical quantum effect, affects the macroscopic properties of gases: ideal gas is the one where these quantum effects are approximately neglected along with the long range mutual interactions as well.
If effectively exists a minimum temperature![]() , then it must be defined by
, then it must be defined by![]() . However, the right hand side is in general function of T itself; indeed it has been shown that
. However, the right hand side is in general function of T itself; indeed it has been shown that![]() , being
, being ![]() the lattice volume available around a given lattice site. So the thermal dilation modifies
the lattice volume available around a given lattice site. So the thermal dilation modifies![]() , whose non-thermal physical meaning however still holds identically. Moreover the local mobility is itself T dependent, as it is intuitive to think; in effect it is known that by self diffusion, atoms in a given lattice point can exchange of place with lattice neighbors, so that the actual volume allowed to a given atom is increased by the number of neighbor elementary cells accessible.
, whose non-thermal physical meaning however still holds identically. Moreover the local mobility is itself T dependent, as it is intuitive to think; in effect it is known that by self diffusion, atoms in a given lattice point can exchange of place with lattice neighbors, so that the actual volume allowed to a given atom is increased by the number of neighbor elementary cells accessible.
These considerations should be also extended in particular to the statistical distributions of bosons and fermions, usually written as a function of kT only: taking into account the considerations elucidated in the case of the Van der Waals equation, one should conclude that strictly speaking in the case of a solid body the simple term kT should be replaced by![]() , where
, where ![]() accounts for the quantum contribution related to the T-dependent zero point energy with
accounts for the quantum contribution related to the T-dependent zero point energy with![]() .
.
![]() (5.32)
(5.32)
Even though the value of ![]() is presumably much lower than the ordinary temperatures today attainable and experimentally measurable, the Equation (5.25) suggests the chance of being tested in a situation where
is presumably much lower than the ordinary temperatures today attainable and experimentally measurable, the Equation (5.25) suggests the chance of being tested in a situation where ![]() is relevant, i.e. in the case of theoretical models of solid state physics. In effect the paper [13] implements the ideas of quantized temperature and statistical distributions (5.32), both introduced as hypotheses; the specific heat calculated agrees very well with the experimental data from very low T up to the melting point for several metals with different crystal structures.
is relevant, i.e. in the case of theoretical models of solid state physics. In effect the paper [13] implements the ideas of quantized temperature and statistical distributions (5.32), both introduced as hypotheses; the specific heat calculated agrees very well with the experimental data from very low T up to the melting point for several metals with different crystal structures.
6. Some Relativistic Corollaries
In this section are examined some relevant relativistic corollaries of the previous results. The importance of the following considerations is shown by the chance of obtaining contextually relativistic results in the same conceptual frame of the quantum results previously obtained. The next two subsections emphasize the importance of the previous equations (3.15) and (4.9), now again under test after their previous validations, see respectively Equations (3.20) and (4.6), (4.7), (4.13) to (4.18).
6.1. The Invariant Interval
Implement the Equation (3.15), once more under test after the result (3.20), rewritten as follows
![]() (6.1)
(6.1)
depending on whether ![]() one has
one has![]() . Hence, squaring both sides,
. Hence, squaring both sides, ![]() reads
reads
![]() (6.2)
(6.2)
where anyway K is the resulting value from the left hand side of the Equation (6.2).
Consider first![]() .
.
Implementing (3.1), one finds
![]()
whence
![]() (6.3)
(6.3)
this equation reads identically
![]() (6.4)
(6.4)
having implemented once more![]() , whereas
, whereas
![]()
reads by dimensional reasons, whatever the value of K might be,
![]() (6.5)
(6.5)
It is easy to recognize the Lorentz transformation of the intervals ![]() and
and ![]() in two different inertial reference systems R and
in two different inertial reference systems R and![]() , hence in (6.4) both
, hence in (6.4) both ![]() and
and ![]() must be invariants, as found in particular in (3.62); indeed K is invariant itself if r of (6.1) is calculated via invariant forms of
must be invariants, as found in particular in (3.62); indeed K is invariant itself if r of (6.1) is calculated via invariant forms of ![]() and p, see Equations (3.64).
and p, see Equations (3.64).
Consider now![]() .
.
The interval defined in (6.3) reads![]() ; moreover (6.2) reads
; moreover (6.2) reads![]() , whence (3.20) with an appropriate value of K. Also this result holds regardless of the local limit condition
, whence (3.20) with an appropriate value of K. Also this result holds regardless of the local limit condition![]() ; so this is not a local property, but a feature of the whole space time. It is significant the fact that these results have been obtained with the help of the quantum uncertainty relationships (3.1).
; so this is not a local property, but a feature of the whole space time. It is significant the fact that these results have been obtained with the help of the quantum uncertainty relationships (3.1).
6.2. The Gravity Force
Consider again the Equation (4.9), now once more under test after its early validation via the Equations (4.6), (4.7) and (4.13) to (4.18). Implementing the Equations (3.1) and the initial definition (2.2) of v one finds
![]()
that yields, after multiplying and dividing the right hand side by an arbitrary mass m,
![]() (6.6)
(6.6)
by dimensional reasons ![]() is an arbitrary length. The function
is an arbitrary length. The function ![]() consists in general of a constant term G plus a correction term
consists in general of a constant term G plus a correction term![]() ; indeed
; indeed ![]() can be expanded in series around arbitrary reference ranges
can be expanded in series around arbitrary reference ranges![]() ,
, ![]() and
and ![]() defining G, i.e.
defining G, i.e.
![]() (6.7)
(6.7)
being ![]() appropriate coefficients of the power series expansion and
appropriate coefficients of the power series expansion and ![]() the sum of the higher order terms of the series. This means calculating
the sum of the higher order terms of the series. This means calculating ![]() around an arbitrary value
around an arbitrary value![]() . So (6.6) reads
. So (6.6) reads
![]() (6.8)
(6.8)
It is evident that the general relativity appears in this result: the Newtonian potential ![]() recognizable in this equation is the approximate particular case of a more general equation involving
recognizable in this equation is the approximate particular case of a more general equation involving ![]() too. It is known for example that the simple addition of a further term to the Newtonian potential is enough to calculate correctly the perihelion precession even without implementing the basic assumptions and tensor calculus of general relativity [14] . Unfortunately the Newton physics does not justify itself this additional term. Nonetheless the mere series expansion of the last (6.6) around an arbitrary space time constant term G legitimates the chance of generalization without introducing “ad hoc” hypotheses. In this respect some further considerations exposed below regard in particular the additional non-Newtonian terms due to the series (6.7), still in the conceptual frame introduced by (1.11) and (1.12) as done throughout this paper. In effect, some papers among which [15] show that the quantum uncertainty allows to infer the most relevant results of general relativity in a unique frame that includes of course the quantum physics. The presence of
too. It is known for example that the simple addition of a further term to the Newtonian potential is enough to calculate correctly the perihelion precession even without implementing the basic assumptions and tensor calculus of general relativity [14] . Unfortunately the Newton physics does not justify itself this additional term. Nonetheless the mere series expansion of the last (6.6) around an arbitrary space time constant term G legitimates the chance of generalization without introducing “ad hoc” hypotheses. In this respect some further considerations exposed below regard in particular the additional non-Newtonian terms due to the series (6.7), still in the conceptual frame introduced by (1.11) and (1.12) as done throughout this paper. In effect, some papers among which [15] show that the quantum uncertainty allows to infer the most relevant results of general relativity in a unique frame that includes of course the quantum physics. The presence of ![]() at the left hand side of (6.8) suggests the chance of multiplying both sides by a further arbitrary mass
at the left hand side of (6.8) suggests the chance of multiplying both sides by a further arbitrary mass![]() ; one finds then
; one finds then
![]() (6.9)
(6.9)
which defines two important quantities
![]() (6.10)
(6.10)
At the left hand side of (6.9) appears the rest energy ![]() of
of ![]() plus a correction term resulting from the series expansion of G, at the right hand side the related potential energy
plus a correction term resulting from the series expansion of G, at the right hand side the related potential energy ![]() to which correspond the pproximate gravitational potential
to which correspond the pproximate gravitational potential ![]() and force
and force ![]() of (6.10) via the constant zero order term
of (6.10) via the constant zero order term ![]() only. Note that the Equations (2.35) and (3.64) have introduced the concept of states of negative energy; hence the left hand sides of (6.9) and (6.10) have physical meaning even regarding
only. Note that the Equations (2.35) and (3.64) have introduced the concept of states of negative energy; hence the left hand sides of (6.9) and (6.10) have physical meaning even regarding ![]() as unique mass
as unique mass ![]() with positive and negative energy states
with positive and negative energy states![]() . So the Equations (4.9) and (3.1) prospect a possible chance for positive sign of
. So the Equations (4.9) and (3.1) prospect a possible chance for positive sign of![]() , i.e. a repulsive gravity force as already found in [16] [17] [18] , whereas (6.9) yields
, i.e. a repulsive gravity force as already found in [16] [17] [18] , whereas (6.9) yields
![]() (6.11)
(6.11)
Consider here the negative value ![]() and suppose
and suppose![]() ; (6.9) and (6.10) yield
; (6.9) and (6.10) yield
![]() (6.12)
(6.12)
The Equations (6.12) and (6.11) will be further explained just below, see the next Equation (8.6), after having first validated the results achieved in this subsection.
1) The Equation (6.8) reads also
![]()
which in the particular case ![]() implies a specific value of
implies a specific value of ![]() given by
given by
![]() (6.13)
(6.13)
To understand the physical meaning of this result, rewrite identically (6.8) multiplying both sides by an arbitrary factor![]() ; then
; then
![]()
For![]() , in particular, one recognizes the well known escape velocity
, in particular, one recognizes the well known escape velocity ![]() of an arbitrary mass
of an arbitrary mass ![]() at a distance
at a distance ![]() from the gravitational center of mass of m, also inferable via (6.12) under the condition of null total energy (potential plus kinetic) of
from the gravitational center of mass of m, also inferable via (6.12) under the condition of null total energy (potential plus kinetic) of ![]() at infinity. As
at infinity. As ![]() is compatible with
is compatible with ![]() simply putting
simply putting ![]() in (6.8), this limit condition for the chance of
in (6.8), this limit condition for the chance of ![]() at distance
at distance ![]() of escaping from the gravity field of m holds also for c. This velocity can be nothing else but that of a photon, so (6.13) shows that at any
of escaping from the gravity field of m holds also for c. This velocity can be nothing else but that of a photon, so (6.13) shows that at any ![]() even light cannot escape from the gravity field of m. Trivial manipulations of the early Equations (4.8) and (4.9) yield therefore the black hole limit condition between mass m and distance
even light cannot escape from the gravity field of m. Trivial manipulations of the early Equations (4.8) and (4.9) yield therefore the black hole limit condition between mass m and distance![]() .
.
2) The present way to introduce the gravity force explains why any test mass ![]() behaves in the same way in the field of a source mass m: the masses m of (6.6) and
behaves in the same way in the field of a source mass m: the masses m of (6.6) and ![]() of (6.9) have been introduced subsequently and independently each other. Note the conceptual difference between the present reasoning and that of the Newtonian approach: Newton has contextually introduced two masses to define their mutual interaction law, here the masses have been consequentially introduced starting from (6.6) because
of (6.9) have been introduced subsequently and independently each other. Note the conceptual difference between the present reasoning and that of the Newtonian approach: Newton has contextually introduced two masses to define their mutual interaction law, here the masses have been consequentially introduced starting from (6.6) because ![]() requires the concept of mass to introduce that of gravitational energy. It is not surprising that once having decided either mass as a field source, the behavior of the other is uniquely fixed: as both masses are independent and arbitrary, once having fixed m the behavior of
requires the concept of mass to introduce that of gravitational energy. It is not surprising that once having decided either mass as a field source, the behavior of the other is uniquely fixed: as both masses are independent and arbitrary, once having fixed m the behavior of ![]() is uniquely determined. In other words there is no reason to expect that any other mass
is uniquely determined. In other words there is no reason to expect that any other mass ![]() behaves in a different way from
behaves in a different way from ![]() in the gravitational field of m because the law governing its dynamics has already been independently fixed.
in the gravitational field of m because the law governing its dynamics has already been independently fixed.
3) Here m and ![]() are regarded in fact as gravitational and inertial masses; the first one defines the gravitational potential
are regarded in fact as gravitational and inertial masses; the first one defines the gravitational potential![]() , the second one defines their mutual interaction force
, the second one defines their mutual interaction force![]() . As they are interchangeable, their gravitational and inertial role is physically equivalent and indistinguishable. Thus gravitational and inertial masses must be equal.
. As they are interchangeable, their gravitational and inertial role is physically equivalent and indistinguishable. Thus gravitational and inertial masses must be equal.
4) Consider that (6.9) and (6.12) yield
![]() (6.14)
(6.14)
Identify now the distance ![]() with one wavelength of a light beam propagating in the vacuum; thus
with one wavelength of a light beam propagating in the vacuum; thus
![]()
Hence, given a light wave propagating at distance![]() , one finds
, one finds
![]()
then
![]() (6.15)
(6.15)
being ![]() a reference frequency of the wave. The first equation defines the famous red shift
a reference frequency of the wave. The first equation defines the famous red shift ![]() of a light wave due to the gravitational potential field change
of a light wave due to the gravitational potential field change![]() .
.
5) It is instructive to consider now two photons freely moving in the vacuum on the diametric plane of two concentric hyperspheres: the inner photon just at radial distance ![]() from the gravity center of m, given by (6.13), the outer photon at any radial distance
from the gravity center of m, given by (6.13), the outer photon at any radial distance ![]() from m. The previous result shows that the inner photon cannot escape from the gravity field of m, so it can move on the surface of the inner hypersphere only, whereas any photon moving at very large distance
from m. The previous result shows that the inner photon cannot escape from the gravity field of m, so it can move on the surface of the inner hypersphere only, whereas any photon moving at very large distance ![]() from m is free to travel unperturbed as a limit case from minus infinity to infinity or vice-versa. Is reasonable the idea that the outer photon moving at the closest approach distance
from m is free to travel unperturbed as a limit case from minus infinity to infinity or vice-versa. Is reasonable the idea that the outer photon moving at the closest approach distance ![]() should follow an intermediate behavior, i.e. a curved space time path bent by m. This preliminary consideration justifies why the problem of light beam bending is tackled here with reference to the previous Equation (6.13). The standard way to approach the problem considers the curved trajectory traveled by the photon that follows the space time curvature along an arc
should follow an intermediate behavior, i.e. a curved space time path bent by m. This preliminary consideration justifies why the problem of light beam bending is tackled here with reference to the previous Equation (6.13). The standard way to approach the problem considers the curved trajectory traveled by the photon that follows the space time curvature along an arc ![]() around m at distance
around m at distance![]() ; the position of the photon before and after its closest approach to m defines the characteristic deflection angle
; the position of the photon before and after its closest approach to m defines the characteristic deflection angle ![]() equal to that formed by the tangents to the osculating circumference at boundaries of
equal to that formed by the tangents to the osculating circumference at boundaries of![]() . From a quantum point of view, however, the concepts of position and trajectory are missing, rather the approach must be similar to that followed to infer (4.16). Just for this reason the present reasoning is instructive to highlight how the quantum requirements are plugged into and provide information on this typical relativistic context.
. From a quantum point of view, however, the concepts of position and trajectory are missing, rather the approach must be similar to that followed to infer (4.16). Just for this reason the present reasoning is instructive to highlight how the quantum requirements are plugged into and provide information on this typical relativistic context.
Regard the arc ![]() of osculating circumference of radius
of osculating circumference of radius ![]() defined by
defined by ![]() conceptually according to of (3.1), i.e. as an uncertainty range where the photon is delocalized. Accordingly
conceptually according to of (3.1), i.e. as an uncertainty range where the photon is delocalized. Accordingly ![]() is actually given by two half angles
is actually given by two half angles ![]() and
and ![]() traveled by the photon along clockwise and counterclockwise paths around the middle point
traveled by the photon along clockwise and counterclockwise paths around the middle point![]() ; indeed the photon displacements implied by
; indeed the photon displacements implied by ![]() and
and ![]() are physically indistinguishable, because nothing is known about the motion features of any particle within an uncertainty range. This point of view skips the idea of a photon entering in
are physically indistinguishable, because nothing is known about the motion features of any particle within an uncertainty range. This point of view skips the idea of a photon entering in ![]() through one boundary and exiting from the other boundary, which in fact would define
through one boundary and exiting from the other boundary, which in fact would define ![]() as an element of trajectory. So
as an element of trajectory. So ![]() waives the whole
waives the whole![]() , which would imply discriminating the events where the photon travels through
, which would imply discriminating the events where the photon travels through ![]() coming from
coming from ![]() towards
towards ![]() or from
or from ![]() towards
towards![]() ; actually these events are indistinguishable likewise the boundaries of
; actually these events are indistinguishable likewise the boundaries of ![]() themselves. So, with respect to gravity center of m, the angle of physical interest is
themselves. So, with respect to gravity center of m, the angle of physical interest is ![]() and not
and not ![]() to account for the sought total
to account for the sought total![]() . In other words the Equations (3.1) compel merging two half-paths into a unique travel path without discriminating either of them.
. In other words the Equations (3.1) compel merging two half-paths into a unique travel path without discriminating either of them.
Consider then an angle ![]() on a circumference of radius
on a circumference of radius ![]() and its related length
and its related length ![]() to describe the uncertainty range
to describe the uncertainty range ![]() where is delocalized the photon. Rewrite the second (6.14) as follows
where is delocalized the photon. Rewrite the second (6.14) as follows
![]()
here the uncertainty ranges ![]() and
and ![]() have been simply rewritten with the usual notation of any
have been simply rewritten with the usual notation of any ![]() by definition, whatever the concerned y might actually be. In this specific case
by definition, whatever the concerned y might actually be. In this specific case ![]() and
and ![]() are two different distances of the photon from the gravity center of m. It is clear that it is convenient to put here
are two different distances of the photon from the gravity center of m. It is clear that it is convenient to put here ![]() because, as previously stated, we are interested to describe the situations where one photon initially unperturbed passes at a finite distance
because, as previously stated, we are interested to describe the situations where one photon initially unperturbed passes at a finite distance ![]() from m. Hence the last equation reads
from m. Hence the last equation reads
![]()
If, for the aforesaid quantum reasons ![]() on the osculating circle, one finds immediately
on the osculating circle, one finds immediately
![]()
These simple considerations emphasize the actual quantum character of one of the most representative relativistic predictions, the gravitational lensing; the famous factor 4 defining ![]() at the right hand side appears to be actually the fingerprint of the quantum uncertainty.
at the right hand side appears to be actually the fingerprint of the quantum uncertainty.
6) Consider the physical dimensions of the gravity constant inferred from (6.6): according to (6.7), space and time range sizes ![]() and
and ![]() concur to its macroscopic value together with the arbitrary mass
concur to its macroscopic value together with the arbitrary mass![]() . From a quantum point of view, (6.7) does not exclude the chance of mass fluctuation, i.e. according to (4.6)
. From a quantum point of view, (6.7) does not exclude the chance of mass fluctuation, i.e. according to (4.6)
![]() (6.16)
(6.16)
Even considering preliminarily the fluctuation of ![]() only, and thus energy fluctuation
only, and thus energy fluctuation ![]() only, the constancy of G is expressible as
only, the constancy of G is expressible as
![]()
i.e. ![]() implies the change of
implies the change of ![]() as well. Note that
as well. Note that ![]() and
and ![]() are not usual dynamical variables characterizing physical laws, rather they define the structure of G itself. In effect, this quantum standpoint implies that transient fluctuations of values of G are in principle possible, being compatible with corresponding space time energy quantum fluctuations
are not usual dynamical variables characterizing physical laws, rather they define the structure of G itself. In effect, this quantum standpoint implies that transient fluctuations of values of G are in principle possible, being compatible with corresponding space time energy quantum fluctuations![]() . Making explicit the right hand side of this last equation, trivial algebraic steps yield
. Making explicit the right hand side of this last equation, trivial algebraic steps yield
![]()
so that ![]() simply if
simply if
![]()
otherwise, e.g. a different correspondence between ![]() and
and ![]() whatever their values might be, the quantum definition of G admits
whatever their values might be, the quantum definition of G admits![]() . All this has clearly to do with the existence of inflationary era of the early Universe: an appropriate fluctuation
. All this has clearly to do with the existence of inflationary era of the early Universe: an appropriate fluctuation ![]() of G can contribute in principle to the sudden increase of expansion rate of the early Universe. Among the implications of these assertions, one deserves particular attention: the possible fluctuations of G affect the black hole length
of G can contribute in principle to the sudden increase of expansion rate of the early Universe. Among the implications of these assertions, one deserves particular attention: the possible fluctuations of G affect the black hole length ![]() of (6.13) of a given m. Unfortunately further discussion on this crucial point is outside the aims of the present paper.
of (6.13) of a given m. Unfortunately further discussion on this crucial point is outside the aims of the present paper.
7) Returning now to the Equations (5.25), the maximum value of momentum wavelength ![]() has been related to a suitable space range
has been related to a suitable space range ![]() defined as the radius of a hypersphere within which is delocalized an arbitrary amount of mass. As the steady wavelength appropriate to calculate the zero point energy
defined as the radius of a hypersphere within which is delocalized an arbitrary amount of mass. As the steady wavelength appropriate to calculate the zero point energy ![]() defining
defining ![]() corresponds to the maximum delocalization extent physically conceivable in our Universe, is reasonable to relate
corresponds to the maximum delocalization extent physically conceivable in our Universe, is reasonable to relate ![]() to the diametric size
to the diametric size ![]() of the Universe, regarded here as a hypersphere with diameter
of the Universe, regarded here as a hypersphere with diameter![]() . So think the mass ideally bouncing within one diametric distance, whose maximum space extent corresponds to one half wavelength; this wave has thus steady nodes at the diametric boundaries of the Universe, regarded in effect as a hypersphere. Replacing
. So think the mass ideally bouncing within one diametric distance, whose maximum space extent corresponds to one half wavelength; this wave has thus steady nodes at the diametric boundaries of the Universe, regarded in effect as a hypersphere. Replacing ![]() of the Equation (5.25) with
of the Equation (5.25) with ![]() and putting
and putting ![]() asymptotically, one finds
asymptotically, one finds
![]() (6.17)
(6.17)
The current estimate ![]() [19] yields the numerical values
[19] yields the numerical values
![]() (6.18)
(6.18)
In addition to the preliminary remarks about the Equation (5.25) previously emphasized, these numerical results suggest further implications:
− Finite Universe means identically![]() .
.
− The limit ![]() would hold in an infinite universe only.
would hold in an infinite universe only.
− To guess the physical meaning of the small value of![]() , note that
, note that ![]() fits surprisingly well the estimated age of the universe
fits surprisingly well the estimated age of the universe ![]() reported in [19] .
reported in [19] .
− The fact that the energy corresponding to ![]() agrees reasonably with the estimated order of magnitude of the age of the universe, suggests that
agrees reasonably with the estimated order of magnitude of the age of the universe, suggests that ![]() with which has been calculated
with which has been calculated ![]() could be a possible vacuum energy fluctuation, still in progress, of the whole Universe.
could be a possible vacuum energy fluctuation, still in progress, of the whole Universe.
− It is interesting that ![]() that determines
that determines ![]() agrees surprisingly well with the Hubble constant.
agrees surprisingly well with the Hubble constant.
8) It is possible to implement these results to calculate another important property of the Universe, i.e. the vacuum energy density![]() . In general, the energy density corresponds from the dimensional point of view to
. In general, the energy density corresponds from the dimensional point of view to![]() . Consider now that according to (6.13) nothing, even the light, can escape from a range size
. Consider now that according to (6.13) nothing, even the light, can escape from a range size ![]() enclosing the mass m; hence, the Equation (6.13) represents a significant opportunity to describe how to trap inside a volume of space time energy that cannot be irradiated nor lost outside it. After having inferred that an energy
enclosing the mass m; hence, the Equation (6.13) represents a significant opportunity to describe how to trap inside a volume of space time energy that cannot be irradiated nor lost outside it. After having inferred that an energy ![]() pervades all Universe, whose zero point value
pervades all Universe, whose zero point value ![]() determines the zero point energy defining
determines the zero point energy defining![]() , is attracting the idea that
, is attracting the idea that ![]() can be calculated just with the value of
can be calculated just with the value of ![]() controlling
controlling![]() . This idea links the vacuum energy density to the zero point energy (5.22) related to
. This idea links the vacuum energy density to the zero point energy (5.22) related to![]() . If so, then calculating
. If so, then calculating ![]() according to (6.13) and implementing
according to (6.13) and implementing ![]() just calculated,
just calculated,
![]() (6.19)
(6.19)
The sensible value of vacuum energy density further supports the way to calculate the values (6.18). This means that the concept of vacuum does not imply that of “nothing”: rather the vacuum must consist of virtual particles whose energy, i.e. mass, governs the residual vacuum energy density in agreement with the third law of thermodynamics.
9) But there is more. Implement the mass ![]() of the part of visible Universe [16] estimated counting the stars only to calculate
of the part of visible Universe [16] estimated counting the stars only to calculate
![]() (6.20)
(6.20)
On the one hand one expects that ![]() is estimated by defect, without taking into account that other forms of energy distributed in the Universe could in principle increase this value; whatever this additional energy
is estimated by defect, without taking into account that other forms of energy distributed in the Universe could in principle increase this value; whatever this additional energy ![]() might be, it concurs with
might be, it concurs with ![]() by
by ![]() to the total mass of the Universe. On the other hand are visible only the stars whose distance does not overcome the observation limit posed by the light speed; assuming that the distribution of galaxies and thus stars is uniform in the Universe, the actual mass due the total number of stars should be
to the total mass of the Universe. On the other hand are visible only the stars whose distance does not overcome the observation limit posed by the light speed; assuming that the distribution of galaxies and thus stars is uniform in the Universe, the actual mass due the total number of stars should be
![]()
This value still estimates the total visible matter of the Universe as if the light speed would be infinite; as such, however, it does not tell anything about other possible contributions inherently “dark”, i.e. non-luminous, for example the vacuum energy/c2 or the zero point energy/c2. Compare thus just this value ![]() with the total mass related to the whole vacuum energy density
with the total mass related to the whole vacuum energy density ![]() calculated above. It is
calculated above. It is
![]()
The total vacuum energy of the Universe is still about 12 times higher than that of all visible objects. Make at this point a hypothesis:
The energy density of vacuum and that of matter are equal, i.e. regard matter and vacuum as two different thermodynamic systems at global equilibrium.
So ![]() must be incremented just by this factor to make equal the respective densities. Write thus the total mass balance as a function of the true visible mass as
must be incremented just by this factor to make equal the respective densities. Write thus the total mass balance as a function of the true visible mass as
![]() (6.21)
(6.21)
the factor 2 accounts for the antimatter, wherever it might be in the Universe, whereas ![]() and
and ![]() are the missing masses also concurring to the factor 12 assumed true. The notations account for the fact that the concept of mass can be defined in general via
are the missing masses also concurring to the factor 12 assumed true. The notations account for the fact that the concept of mass can be defined in general via ![]() and
and![]() . Rewrite now these positions with the help of (2.36)
. Rewrite now these positions with the help of (2.36)
![]() (6.22)
(6.22)
where ![]() and
and ![]() are the pertinent momentum wavelength and energy frequency. Thus
are the pertinent momentum wavelength and energy frequency. Thus
![]() (6.23)
(6.23)
being ![]() arbitrary velocity. Moreover rewrite identically (6.21) as
arbitrary velocity. Moreover rewrite identically (6.21) as
![]() (6.24)
(6.24)
where ![]() and
and ![]() are appropriate coefficients able to express numerically
are appropriate coefficients able to express numerically ![]() and
and ![]() via
via![]() . Actually the physical meaning of these positions is to establish a relationship between visible mass and the other contributions to
. Actually the physical meaning of these positions is to establish a relationship between visible mass and the other contributions to![]() . The last position, in particular, is possible because
. The last position, in particular, is possible because ![]() and
and ![]() are arbitrary. One equation to determine these coefficients is obviously
are arbitrary. One equation to determine these coefficients is obviously
![]() (6.25)
(6.25)
Moreover, as (6.23) reads
![]() (6.26)
(6.26)
(6.24) yields
![]() (6.27)
(6.27)
and thus ![]() and
and![]() . Being the third position (6.26) certainly fulfilled via the arbitrary
. Being the third position (6.26) certainly fulfilled via the arbitrary![]() , which however does not appear in (6.27), (6.24) and (6.21) become
, which however does not appear in (6.27), (6.24) and (6.21) become
![]()
which are expressed more significantly in relative![]() :
:
![]() (6.28)
(6.28)
The papers [10] propose a possible explanation, here omitted for brevity, about why matter and antimatter are separated. It is more important to note that there is no “ad hoc” hypothesis in this reasoning, rather a further implication of the fundamental concept of uncertainty repeatedly invoked throughout all this paper and again exploited here through the assumption of vacuum/matter equilibrium. In effect the mass densities calculable via the terms ![]() and
and ![]() additional to
additional to ![]() in (6.21) correspond to the respective energy densities and thus to pressure terms inside the Universe. The next Equations (8.28) to (8.34) elucidate this point.
in (6.21) correspond to the respective energy densities and thus to pressure terms inside the Universe. The next Equations (8.28) to (8.34) elucidate this point.
10) Multiply (6.6) by the mass ![]() introduced in (3.20) and (3.21); recalling the second (3.26) it is possible to write
introduced in (3.20) and (3.21); recalling the second (3.26) it is possible to write
![]() (6.29)
(6.29)
which links via ![]() the Newtonian gravity and quantum energy at the left hand side. Whatever
the Newtonian gravity and quantum energy at the left hand side. Whatever ![]() might be, the arbitrary distance
might be, the arbitrary distance ![]() is repalced by arbitrary quantum numbers n and
is repalced by arbitrary quantum numbers n and![]() . In this sense (3.20) is reasonably defined in [6] as equation of quantum gravity.
. In this sense (3.20) is reasonably defined in [6] as equation of quantum gravity.
It is true that actually G should be replaced by ![]() to plug all considerations carried out in the subsection 6.2 into the relativistic realm via (6.7); but it is also true that actually
to plug all considerations carried out in the subsection 6.2 into the relativistic realm via (6.7); but it is also true that actually ![]() has been defined in order to make
has been defined in order to make ![]() and
and ![]() of Equation (3.15) consistent with the harmonic oscillator form (3.25) consequent (3.24). Modifying the definitions (3.23) in order to define non-harmonic oscillations would mean adding additional correction terms corresponding to the higher order terms of the series (6.7). It is possible to say shortly that the Newton gravitational energy corresponds to quantum harmonic oscillators at the left hand side of (3.25), the relativistic gravity is described by non-harmonic oscillator terms replacing the mere
of Equation (3.15) consistent with the harmonic oscillator form (3.25) consequent (3.24). Modifying the definitions (3.23) in order to define non-harmonic oscillations would mean adding additional correction terms corresponding to the higher order terms of the series (6.7). It is possible to say shortly that the Newton gravitational energy corresponds to quantum harmonic oscillators at the left hand side of (3.25), the relativistic gravity is described by non-harmonic oscillator terms replacing the mere ![]() of (3.25).
of (3.25).
7. Klein Gordon, Proca and Maxwell Equations
Implement now the Equations (3.30) introducing a function of ![]() defined as follows
defined as follows
![]() (7.1)
(7.1)
where ![]() and Q are arbitrary constants. So the first Equation (3.30) yields
and Q are arbitrary constants. So the first Equation (3.30) yields
![]() (7.2)
(7.2)
proceeding in analogous way with the help of (3.31), the second Equation (3.30) yields
![]() (7.3)
(7.3)
Hence, replacing (7.3) and (7.2) in the right hand side of (3.32), the result is an equation expressed as a function of the functional ![]() of
of ![]()
![]() (7.4)
(7.4)
as m appears at the left hand side only of (3.32), it has been included in ![]() together with the factor
together with the factor ![]() without loss of generality. Taking the limit
without loss of generality. Taking the limit![]() , which by consequence implies
, which by consequence implies ![]() as well, this one dimensional result is actually the well known Klein Gordon equation
as well, this one dimensional result is actually the well known Klein Gordon equation
![]()
On the one hand it confirms the validity of the positions (3.30) and thus of (3.39) too; on the other hand this result shows that the Klein Gordon equation is inferred from the local functional (7.1) of the space time function (3.39). The latter equation simply rewrites the former according to the usual 4D d’Alabertian.
This result can be further generalized taking advantage that the last equation is actually expressed as a function of ![]() and not of the initial m. The fact that
and not of the initial m. The fact that ![]() can take two values depending on either sign in (7.3) suggests that in fact two equations are tacitly implied by the unique Equation (7.1); for example one scalar equation and one vector equation should be compatible with (7.3). This is very easily proven showing that the scalar and vector fields of the Proca equations can be combined into one resulting Klein Gordon-like equation. The most straightforward way to demonstrate this assertion starts just from the Proca equations
can take two values depending on either sign in (7.3) suggests that in fact two equations are tacitly implied by the unique Equation (7.1); for example one scalar equation and one vector equation should be compatible with (7.3). This is very easily proven showing that the scalar and vector fields of the Proca equations can be combined into one resulting Klein Gordon-like equation. The most straightforward way to demonstrate this assertion starts just from the Proca equations
![]()
which actually, owing to the definition of the operator![]() , read respectively
, read respectively
![]() (7.5)
(7.5)
thus ![]() and
and ![]() are the sought scalar and vector fields linking the two equations. Multiply the former equation by an arbitrary function
are the sought scalar and vector fields linking the two equations. Multiply the former equation by an arbitrary function ![]() and the latter by an arbitrary velocity vector
and the latter by an arbitrary velocity vector![]() , i.e.
, i.e.
![]()
Subtracting side by side these equations,
![]() (7.6)
(7.6)
trivial algebraic steps yield the following scalar equation
![]() (7.7)
(7.7)
As f is an arbitrary function, it can be defined in order that
![]() (7.8)
(7.8)
hence
![]() (7.9)
(7.9)
Eventually it is possible to infer from this equation
![]() (7.10)
(7.10)
both f and ![]() are arbitrary, thus the last position just introduced is in fact possible. Actually the first (7.10) does not depend on f and has still the form of a Klein Gordon-like equation for the previous scalar function
are arbitrary, thus the last position just introduced is in fact possible. Actually the first (7.10) does not depend on f and has still the form of a Klein Gordon-like equation for the previous scalar function![]() , where appears however the factor
, where appears however the factor ![]() at the right hand side corresponding to the previous
at the right hand side corresponding to the previous ![]() of (7.3). Just this factor is the key to split this double valued equation: indeed
of (7.3). Just this factor is the key to split this double valued equation: indeed ![]() is one scalar equation, whereas the additional chance
is one scalar equation, whereas the additional chance ![]() allows inferring the couple of Proca equations via the position
allows inferring the couple of Proca equations via the position ![]() that introduces the vector field
that introduces the vector field![]() . It is enough to revert the steps from (7.10) to (7.5) still via the key position (7.8). The profound physical meaning of this position, here purposely introduced to obtain (7.9), is shortly outlined below, to show that it is not merely a useful algebraic step.
. It is enough to revert the steps from (7.10) to (7.5) still via the key position (7.8). The profound physical meaning of this position, here purposely introduced to obtain (7.9), is shortly outlined below, to show that it is not merely a useful algebraic step.
The Equation (7.8) reads
![]() (7.11)
(7.11)
i.e.
![]() (7.12)
(7.12)
In this equation it is possible to put formally
![]() (7.13)
(7.13)
the first position is the Lorentz condition, the second equation is the definition of the new quantity![]() , the third equation is obtained replacing
, the third equation is obtained replacing ![]() at the right hand side of (7.11) and simply means that
at the right hand side of (7.11) and simply means that ![]() is orthogonal to
is orthogonal to ![]() to get
to get ![]() at both sides. Now give
at both sides. Now give ![]() physical meaning introducing the following positions
physical meaning introducing the following positions
![]() (7.14)
(7.14)
the first position is simply the definition of a new quantity![]() , whence follows the second equation by consequence; the third equation is obtained taking
, whence follows the second equation by consequence; the third equation is obtained taking ![]() of both sides of the second (7.13). Note now that the first and second (7.13) yield
of both sides of the second (7.13). Note now that the first and second (7.13) yield
![]() (7.15)
(7.15)
Eventually it is possible to infer a fourth equation considering the continuity condition ![]() of an arbitrary function
of an arbitrary function![]() , which reads
, which reads![]() ; thus the one dimensional expression
; thus the one dimensional expression![]() , where v must be intended of course as
, where v must be intended of course as![]() , reads in general
, reads in general![]() . Hence
. Hence ![]() yields
yields
![]()
Since g has not yet been defined, it is possible to rewrite this equation implementing the scalars already inferred, to obtain a self-contained set of equations. Put
![]()
which yields therefore
![]()
It is convenient to utilize the vector property ![]() in agreement with
in agreement with ![]() of solenoidal flux of
of solenoidal flux of ![]() to simplify this last equation whatever the arbitrary field
to simplify this last equation whatever the arbitrary field ![]() might be. Thus one obtains
might be. Thus one obtains
![]() (7.16)
(7.16)
Despite the lack of specific information to identify the actual nature of![]() , it is reasonable to put
, it is reasonable to put ![]() with
with ![]() magnetic field to be introduced just in the next section: this position is in fact possible without introducing a new field, hardly justifiable in the present context. Hence the position (7.8) is valuable as it implies four relevant equations, whose importance appears by answering questions like: flux of what? what kind of fields are
magnetic field to be introduced just in the next section: this position is in fact possible without introducing a new field, hardly justifiable in the present context. Hence the position (7.8) is valuable as it implies four relevant equations, whose importance appears by answering questions like: flux of what? what kind of fields are ![]() and
and![]() ? The next section clarifies these points that clearly allow to obtain the Maxwell equations (7.14), (7.15) and (7.16).
? The next section clarifies these points that clearly allow to obtain the Maxwell equations (7.14), (7.15) and (7.16).
These fields allow modifying appropriately the functional (7.1), in order to describe one particle even via a possible interaction potential; of course such a calculation is omitted here for brevity, being clearly beyond the purposes of the present paper.
8. The Fundamental Interactions of Nature: Force Laws
Some considerations about the gravity force in the subsection 6.2 were inferred starting from the Equation (4.9). Now the concept of force is reexamined starting from the more general Equations (3.1) and (3.69). This section consists of three subsections.
8.1. Preliminary Considerations
The Equations (3.1) provide several chances of defining the general concept of force, directly related to (3.69) and (3.70)
![]() (8.1)
(8.1)
whence, implementing once more![]() , one infers in general
, one infers in general
![]() (8.2)
(8.2)
To understand intuitively the correlation between F and![]() , think that the effect of any force is to modify the state of motion of matter on which it acts. Consider a body of mass m under the action of a force F. If m is actually a system of particles, then F perturbs the dynamics of all particles of m: for example they move faster. According to (3.1), modifying the kinetic energy of a system of particles implies changing in principle their delocalization extent and thus the range size
, think that the effect of any force is to modify the state of motion of matter on which it acts. Consider a body of mass m under the action of a force F. If m is actually a system of particles, then F perturbs the dynamics of all particles of m: for example they move faster. According to (3.1), modifying the kinetic energy of a system of particles implies changing in principle their delocalization extent and thus the range size ![]() able to include each one of them. The greater the force altering the status of a system, the greater must be the size change rate
able to include each one of them. The greater the force altering the status of a system, the greater must be the size change rate ![]() to account for the altered delocalization extent of matter in
to account for the altered delocalization extent of matter in![]() . This is the intuitive way to justify in general the quantum link between F and the related
. This is the intuitive way to justify in general the quantum link between F and the related![]() . More specifically (8.1) also imply
. More specifically (8.1) also imply
![]() (8.3)
(8.3)
the inequality is direct consequence of the first equation with ![]() replaced by
replaced by![]() . Again, the position
. Again, the position ![]() yields the usual definition of generalized local force
yields the usual definition of generalized local force![]() . These equations are directly referable to long range interactions, because
. These equations are directly referable to long range interactions, because ![]() is defined even at infinity in lack of specific constrains; being directly inferred from the general Equations (3.1), F is expected to hold for charged and neutral particles. In effect the Newton and Coulomb forces represent an important class of forces that vanish at infinity as
is defined even at infinity in lack of specific constrains; being directly inferred from the general Equations (3.1), F is expected to hold for charged and neutral particles. In effect the Newton and Coulomb forces represent an important class of forces that vanish at infinity as![]() , justifiable simply assuming
, justifiable simply assuming![]() ; is evident the analogy of (8.2) with
; is evident the analogy of (8.2) with ![]() of (6.10).
of (6.10).
Beside (8.2), particularly interesting are further dimensional considerations about characteristic space and time ranges related some specific forces. Write for example
![]() (8.4)
(8.4)
the first definition follows from![]() . The Equations (8.4) and (8.3) prospect the chance of introducing the concept of short range force as that related to characteristic lengths, times and possibly volume consistently with the Equations (3.1). An example in this respect is the zero point energy resulting from the confinement of matter in a finite volume of space time, already introduced in (5.23); another example is the Casimir force, shortly sketched below.
. The Equations (8.4) and (8.3) prospect the chance of introducing the concept of short range force as that related to characteristic lengths, times and possibly volume consistently with the Equations (3.1). An example in this respect is the zero point energy resulting from the confinement of matter in a finite volume of space time, already introduced in (5.23); another example is the Casimir force, shortly sketched below.
The ranges ![]() and
and ![]() of (8.4) help to fix the energy scale or the distance scale characteristic of specific interactions. Are useful in this respect the values (3.12) of length ranges; the Equations (8.4) are implementable with these scale lengths of prospective interest to estimate the strength of short range forces.
of (8.4) help to fix the energy scale or the distance scale characteristic of specific interactions. Are useful in this respect the values (3.12) of length ranges; the Equations (8.4) are implementable with these scale lengths of prospective interest to estimate the strength of short range forces.
The few remarks exposed here highlight how to proceed in various cases. First of all, it is necessary to examine how long range and short range forces are included in the general definition (8.1) of F: the key point is the deformation rate ![]() of the space time range
of the space time range![]() .
.
Let two interacting partners be ![]() apart and expand in series
apart and expand in series![]() : this position ensures that F vanishes at
: this position ensures that F vanishes at![]() . Write thus in general
. Write thus in general
![]() (8.5)
(8.5)
where A and B are the constant coefficients of the series expansions. So (8.2) splits into the sum of various terms
![]()
Here ![]() by definition, with signs of
by definition, with signs of ![]() dependent on whether
dependent on whether ![]() swells or shrinks during
swells or shrinks during![]() . The Equation (8.5) is more general than (6.7): the latter concerns specifically
. The Equation (8.5) is more general than (6.7): the latter concerns specifically ![]() and thus the gravity, i.e.
and thus the gravity, i.e. ![]() corresponds to
corresponds to![]() , whereas (8.5) instead concerns more in general
, whereas (8.5) instead concerns more in general![]() ; the higher order terms expressing
; the higher order terms expressing ![]() include
include ![]() of (6.7). Just to show this point the coefficients A and B have been split introducing constants lengths
of (6.7). Just to show this point the coefficients A and B have been split introducing constants lengths ![]() that characterize various kinds of forces in fact included in (8.2) and made explicit by the respective terms of the series expansion of F. Examine thus one by one the forces resulting from the first three terms of (8.5) to show that in effect this approach is interpretable in a sensible way. The first force identifiable is
that characterize various kinds of forces in fact included in (8.2) and made explicit by the respective terms of the series expansion of F. Examine thus one by one the forces resulting from the first three terms of (8.5) to show that in effect this approach is interpretable in a sensible way. The first force identifiable is
![]() (8.6)
(8.6)
where the subscript NC stands for Newton Coulomb. The second and third forces easily identifiable are
![]()
having inferred ![]() by comparison with (5.23), and
by comparison with (5.23), and
![]()
One finds again the zero point force controlled by the Compton length ![]() of the mass m. Moreover one recognizes the Casimir force per unit surface
of the mass m. Moreover one recognizes the Casimir force per unit surface ![]() given by
given by ![]() times the pertinent numerical factor
times the pertinent numerical factor ![]() whose value is controlled by
whose value is controlled by ![]() whatever the value of
whatever the value of ![]() contributing to
contributing to ![]() might be. In this way neither
might be. In this way neither ![]() nor
nor ![]() and
and ![]() result fixed; so the second and third terms of (8.6) are the higher order terms of the zero order approximation
result fixed; so the second and third terms of (8.6) are the higher order terms of the zero order approximation ![]() in principle definable by these lengths independently of the coefficients characterizing
in principle definable by these lengths independently of the coefficients characterizing ![]() and force per unit surface
and force per unit surface![]() . The zero point energy has been already concerned; a detailed discussion of the Casimir term is clearly outside the purposes of the present paper. It is really crucial the fact that various kinds of forces are nested in the general uncertainty Equation (8.2), in turn direct consequence of (2.10). Owing to the importance of (8.6), the following consideration will be focused on this equation for sake of brevity only; this allows to complete the information in Section 6.2.
. The zero point energy has been already concerned; a detailed discussion of the Casimir term is clearly outside the purposes of the present paper. It is really crucial the fact that various kinds of forces are nested in the general uncertainty Equation (8.2), in turn direct consequence of (2.10). Owing to the importance of (8.6), the following consideration will be focused on this equation for sake of brevity only; this allows to complete the information in Section 6.2.
8.2. Long Range Gravity Force
To verify how (8.6) implies more specifically the space time curvature, examine both sides of the general Equation (8.2). The Equations (3.1) imply the following chain of equations implementing the left hand side of (8.2)
![]() (8.7)
(8.7)
![]()
being ![]() the Laplace average curvature radius of an ideal surface such that
the Laplace average curvature radius of an ideal surface such that ![]() for
for ![]() and
and![]() .
.
Note that ![]() is formally similar to
is formally similar to![]() , where the addends are defined on two orthogonal planes called curvature sections; it refers to flat space time. According to its classical derivation, the local value of
, where the addends are defined on two orthogonal planes called curvature sections; it refers to flat space time. According to its classical derivation, the local value of ![]() is calculable as both radii
is calculable as both radii ![]() and
and ![]() are assumed in principle exactly knowable. Here, instead, the quantum derivation of
are assumed in principle exactly knowable. Here, instead, the quantum derivation of ![]() does not allow any information about size and even mutual orientation of
does not allow any information about size and even mutual orientation of ![]() and
and![]() , the only indication available being that it is conceptually defined by two curvature sections in a 4D space time; so
, the only indication available being that it is conceptually defined by two curvature sections in a 4D space time; so ![]() is not calculable in practice, it is compatible with all combination of values included within
is not calculable in practice, it is compatible with all combination of values included within ![]() and
and![]() . The relativistic curvature
. The relativistic curvature ![]() is instead self-defined in a Gauss curvilinear coordinates in a covariant way regardless of the reference system. According to (3.2), however, even
is instead self-defined in a Gauss curvilinear coordinates in a covariant way regardless of the reference system. According to (3.2), however, even ![]() defined by two uncertainty ranges actually waives the link to a specific reference system; hence the impossibility of calculating uniquely
defined by two uncertainty ranges actually waives the link to a specific reference system; hence the impossibility of calculating uniquely ![]() prevents comparing it to
prevents comparing it to![]() , whose local value is instead in principle calculable. Hence is meaningless to enquiry whether or not the Equation (8.7) fits the standard definition of general relativity or not. In other words
, whose local value is instead in principle calculable. Hence is meaningless to enquiry whether or not the Equation (8.7) fits the standard definition of general relativity or not. In other words ![]() must be necessarily covariant to have physical meaning, because effectively it can be calculable locally;
must be necessarily covariant to have physical meaning, because effectively it can be calculable locally; ![]() instead fulfills the quantum concept of covariance required by (3.2) and cannot take any deterministic value. Hence, in lack of numerical assessment, the quantum reasoning implied by (8.7) allows conceptual comparison only: the quantum definition of space time curvature, although symbolic, is still related to its relationship with F, i.e.
instead fulfills the quantum concept of covariance required by (3.2) and cannot take any deterministic value. Hence, in lack of numerical assessment, the quantum reasoning implied by (8.7) allows conceptual comparison only: the quantum definition of space time curvature, although symbolic, is still related to its relationship with F, i.e. ![]() for
for ![]() and
and ![]() both finite. The non trivial implication of this reasoning is that in this way the relativity becomes a corollary of (3.1) and (8.2) via the series expansion (8.5) that generalizes the mere Newtonian term. This is not surprising because the Section 1 has evidenced the 4D holistic character of the present model; the purpose of the next considerations is to clarify further this idea.
both finite. The non trivial implication of this reasoning is that in this way the relativity becomes a corollary of (3.1) and (8.2) via the series expansion (8.5) that generalizes the mere Newtonian term. This is not surprising because the Section 1 has evidenced the 4D holistic character of the present model; the purpose of the next considerations is to clarify further this idea.
Recalling (2.36)![]() , the right hand side of (8.2) yields, owing to (4.24) and (2.36),
, the right hand side of (8.2) yields, owing to (4.24) and (2.36),
![]() (8.8)
(8.8)
so, merging (8.7) and (8.8), one finds
![]() (8.9)
(8.9)
No apparent reference to the mass is explicitly evident in this formula: the force ![]() and its approximation
and its approximation ![]() are due to the mere deformation rate of the range
are due to the mere deformation rate of the range![]() .
.
On the one hand (8.2) results consistent with this equation that links force ![]() and energy
and energy ![]() via the curvature radius
via the curvature radius ![]() of space time: as expected the momentum, and thus its time change as well, can be expressed via corpuscle formalism, see e.g. (3.64), and via wave formalism inferred in (2.36). Accordingly
of space time: as expected the momentum, and thus its time change as well, can be expressed via corpuscle formalism, see e.g. (3.64), and via wave formalism inferred in (2.36). Accordingly ![]() waives the concept of mass if just (2.36) is implemented to calculate
waives the concept of mass if just (2.36) is implemented to calculate![]() . The analogy with (8.6) and (8.5) appears because also now it is possible to write
. The analogy with (8.6) and (8.5) appears because also now it is possible to write
![]() (8.10)
(8.10)
this is the meaning of the Equations (8.7) to (8.9), where the mass is mere dimensional property of h.
On the other hand, the connection of (8.6) with (6.12) implied by (6.7) requires writing
![]() (8.11)
(8.11)
the curvature ![]() is linked to one mass, that defining
is linked to one mass, that defining ![]() and
and ![]() of (8.9), the zero order deformation rate
of (8.9), the zero order deformation rate ![]() of
of ![]() is given by the constant
is given by the constant ![]() times the product
times the product![]() , i.e.
, i.e. ![]() is proportional to
is proportional to ![]() that in turn is directly proportional to the force. The Equations (8.6) and (8.11) are the space time/matter formulations of the gravity force analogous to the wave/corpuscle formulations of the energy and momentum in quantum mechanics; in effect (3.70) has shown that in general the force is proportional to
that in turn is directly proportional to the force. The Equations (8.6) and (8.11) are the space time/matter formulations of the gravity force analogous to the wave/corpuscle formulations of the energy and momentum in quantum mechanics; in effect (3.70) has shown that in general the force is proportional to![]() .
.
It turns out therefore from the previous considerations with the help of (2.36)
![]() (8.12)
(8.12)
whence the correlations
![]() (8.13)
(8.13)
Comparing the left and right hand sides of both (8.12), is evident why Einstein has successfully replaced the concept of force with that of space time curvature, while skipping the more intuitive Newtonian correspondence between mass and force: thus, in His intuition, the mass appears directly related to the space time curvature. So the first correlation (8.13) is understandable. The second correlation deserves attention, as the concept of acceleration has been not yet introduced; it will be concerned in the next subsection in particular to explain what have to do ![]() or
or ![]() with the acceleration implied by F. It will be shown that just the ranges, which link the concept of force to the quantum uncertainty, also plug the Newton and Coulomb forces into the realm of quantum mechanics.
with the acceleration implied by F. It will be shown that just the ranges, which link the concept of force to the quantum uncertainty, also plug the Newton and Coulomb forces into the realm of quantum mechanics.
8.3. The Equivalence Principle
Implement the Equations (8.11) and (8.8) to understand why the mass appears in the former and not in the latter. Also this topic, shortly sketched here for completeness, has been concerned in [10] .
Position and size of any ![]() in an arbitrary R are respectively definable considering the distance of either range boundary, say
in an arbitrary R are respectively definable considering the distance of either range boundary, say![]() , from the origin O and the distance of x from
, from the origin O and the distance of x from![]() ; of course the opposite choice would be identically admissible. Being both boundaries arbitrary, in general it is possible to regard
; of course the opposite choice would be identically admissible. Being both boundaries arbitrary, in general it is possible to regard ![]() and
and![]() . A force F arises inside
. A force F arises inside ![]() because in general
because in general![]() , i.e. when the range size of
, i.e. when the range size of ![]() shrinks or stretches as a function of time during
shrinks or stretches as a function of time during ![]() with respect to its initial size at the time
with respect to its initial size at the time![]() . To simplify the reasoning it is enough to examine the cases where: 1)
. To simplify the reasoning it is enough to examine the cases where: 1) ![]() and
and ![]() only or 2)
only or 2) ![]() and
and ![]() only; as anyway the size of
only; as anyway the size of ![]() changes, for example because of energy fluctuation of a particle inside
changes, for example because of energy fluctuation of a particle inside![]() , both cases imply in general
, both cases imply in general ![]() and the following considerations about inertial and accelerated reference systems.
and the following considerations about inertial and accelerated reference systems.
Imagine an observer sitting on ![]() and assume for simplicity that one particle only is delocalized in
and assume for simplicity that one particle only is delocalized in![]() ; the rising of any F is detected observing the dynamical behavior of this test particle.
; the rising of any F is detected observing the dynamical behavior of this test particle.
In the case (1) the observer is by definition at rest in R with respect to O; yet he acknowledges a force ![]() acting on the particle, actually due to
acting on the particle, actually due to![]() . To justify in principle why the motion of the particle is perturbed, the observer reasonably thinks to the presence of an external force, e.g. a gravitational mass outside
. To justify in principle why the motion of the particle is perturbed, the observer reasonably thinks to the presence of an external force, e.g. a gravitational mass outside![]() .
.
In the case (2) the observer no longer at rest in R necessarily accelerates with respect to O, whereas the force ![]() again appears in
again appears in ![]() according to
according to![]() ; now
; now ![]() governs the dynamics of the particle delocalized in
governs the dynamics of the particle delocalized in![]() . The observer concludes that its own acceleration is due to
. The observer concludes that its own acceleration is due to![]() .
.
Of course the analytical forms of F and ![]() are in principle analogous, although their strengths are in general different if
are in principle analogous, although their strengths are in general different if![]() ; indeed the forces only differ by the time dependence of either boundary coordinate of
; indeed the forces only differ by the time dependence of either boundary coordinate of ![]() with which is calculated the overall
with which is calculated the overall![]() . However, despite the boundaries of
. However, despite the boundaries of ![]() are in general arbitrary and independent each other, nothing hinders to assume in particular
are in general arbitrary and independent each other, nothing hinders to assume in particular![]() : i.e. stretching of
: i.e. stretching of ![]() occurs via forwards displacement of x only or backwards displacement of
occurs via forwards displacement of x only or backwards displacement of ![]() only with respect to O. So locally
only with respect to O. So locally![]() . The acceleration experienced by the observer and the presumed force F arising outside
. The acceleration experienced by the observer and the presumed force F arising outside ![]() perturb in the same way the test mass because they have actually a unique background, the deformation rate (8.5) of the space time range
perturb in the same way the test mass because they have actually a unique background, the deformation rate (8.5) of the space time range ![]() itself that in effect implies (8.6): in (2) this deformation rate is perceptible by the observer as force
itself that in effect implies (8.6): in (2) this deformation rate is perceptible by the observer as force ![]() whereas in (1) it does not, although in both cases the observer can anyway record the same change of local dynamics of the particle inside
whereas in (1) it does not, although in both cases the observer can anyway record the same change of local dynamics of the particle inside![]() . Clearly the observer reference system
. Clearly the observer reference system ![]() with origin on
with origin on ![]() is at rest or inertial in (1) but non-inertial in (2) with respect to R, in agreement with the aforesaid correlation.
is at rest or inertial in (1) but non-inertial in (2) with respect to R, in agreement with the aforesaid correlation.
One key point of the reasoning is that these conclusions hold exchanging the role of x and![]() , because both range boundaries are arbitrary and physically equivalent; no physical property characterizes specifically either space time boundary displacement. As (1) and (2) are physically indistinguishable, the unique information available is the overall deformation rate
, because both range boundaries are arbitrary and physically equivalent; no physical property characterizes specifically either space time boundary displacement. As (1) and (2) are physically indistinguishable, the unique information available is the overall deformation rate ![]() and its related F; this means that the concept of acceleration implied by
and its related F; this means that the concept of acceleration implied by ![]() holds identically for F as well. Another key point is that the acceleration does not necessarily imply the concept of mass, but that of force in turn due to inertial and non-inertial reference systems.
holds identically for F as well. Another key point is that the acceleration does not necessarily imply the concept of mass, but that of force in turn due to inertial and non-inertial reference systems.
One could also say that the concept of force is redundant, what in fact exists is the stretching/shrinking rate of ![]() which in turn implies space time curvature according to (8.7). But now this statement has quantum foundation only.
which in turn implies space time curvature according to (8.7). But now this statement has quantum foundation only.
Anyway the dualism wave/corpuscle of quantum mechanics has relativistic analogy in the “corpuscular” Equation (6.9) and “wave” Equation (8.9) properties of matter; the latter originates from the space time curvature, the former from the necessity of defining the change of delocalization extent of massless or massive particles both contextually implied by the probabilistic Equation (4.7). In this sense quantum and relativistic physics are perfectly symmetrical, which is not surprising because both are rooted on the quantum uncertainty. From this analogy follow the correspondences (8.12) along with the Equations (6.28) and the various forces implied by (8.5).
Is evident the analogy of ![]() with the elevator of Einstein’s thought experiment: the cases of inertial and non-inertial reference systems merge here into the unknown and unknowable behavior of the boundaries of a unique space time uncertainty range
with the elevator of Einstein’s thought experiment: the cases of inertial and non-inertial reference systems merge here into the unknown and unknowable behavior of the boundaries of a unique space time uncertainty range ![]() only. Implementing space time ranges rather than local space time coordinates plugs a typical relativistic reasoning about inertial and non-inertial reference systems into the quantum uncertainty (3.1). In this sense the relativity is conceptually compatible with quantum requirements; any reasoning via local coordinates, e.g. the tensor calculus, wouldn’t. The present approach shows what the mere wave formalism to quantum mechanics cannot emphasize itself: quantum and relativistic theories are conceptually rooted in the unique concept of uncertainty, the operator formalism exposed in the subsection 3.5 is instead less general being actually itself a corollary of the quantum uncertainty.
only. Implementing space time ranges rather than local space time coordinates plugs a typical relativistic reasoning about inertial and non-inertial reference systems into the quantum uncertainty (3.1). In this sense the relativity is conceptually compatible with quantum requirements; any reasoning via local coordinates, e.g. the tensor calculus, wouldn’t. The present approach shows what the mere wave formalism to quantum mechanics cannot emphasize itself: quantum and relativistic theories are conceptually rooted in the unique concept of uncertainty, the operator formalism exposed in the subsection 3.5 is instead less general being actually itself a corollary of the quantum uncertainty.
8.4. Long Range Electromagnetic Interactions
Start from the Equation (4.8) ![]() and the position (4.9)
and the position (4.9)![]() , which now are once more under test besides to the results (4.13), (4.14), (4.16) and (4.17) already obtained; the Equation (4.9) was also the starting point of the section 6.2. Recalling the definition (4.5) of refractive index n, elementary manipulations yield
, which now are once more under test besides to the results (4.13), (4.14), (4.16) and (4.17) already obtained; the Equation (4.9) was also the starting point of the section 6.2. Recalling the definition (4.5) of refractive index n, elementary manipulations yield
![]() (8.14)
(8.14)
being of course ![]() an arbitrary length. The second equality is the mere definition of energy range
an arbitrary length. The second equality is the mere definition of energy range ![]() with arbitrary boundary values
with arbitrary boundary values ![]() and
and![]() . A possible way to split accordingly
. A possible way to split accordingly ![]() too, is to rewrite (8.14) defining
too, is to rewrite (8.14) defining ![]() and
and ![]() as follows
as follows
![]() (8.15)
(8.15)
to obtain next (8.14) rewritten as
![]() (8.16)
(8.16)
the positions (8.15) convert thus the unique term at the left hand side of (8.14) into the difference of energies ![]() and
and ![]() defining
defining![]() . In general
. In general![]() . Let
. Let ![]() measure the distance between two interacting partners. The fact that
measure the distance between two interacting partners. The fact that ![]() is defined by c means that the carriers of the force are massless particles, photons. Also, v that defines the energy range (8.14) characterizing this kind of interaction must be consistently identified by
is defined by c means that the carriers of the force are massless particles, photons. Also, v that defines the energy range (8.14) characterizing this kind of interaction must be consistently identified by![]() ; as any
; as any ![]() could not be enough to travel through
could not be enough to travel through![]() , a coherent way to characterize the peculiar value of q consistent with
, a coherent way to characterize the peculiar value of q consistent with ![]() requires the boundary condition
requires the boundary condition ![]() in (8.16). Put thus the resulting value of q, now uniquely defined, proportional to a “new” quantity called e. So, calling
in (8.16). Put thus the resulting value of q, now uniquely defined, proportional to a “new” quantity called e. So, calling ![]() the dimensionless proportionality constant linking
the dimensionless proportionality constant linking ![]() and
and![]() , (8.16) yields
, (8.16) yields
![]() (8.17)
(8.17)
Multiplying both sides by ![]() one finds
one finds
![]()
as a result we have obtained the definition of fine structure constant ![]() via three universal constants of the nature, whereas
via three universal constants of the nature, whereas ![]() is to be regarded as a pure number corresponding to the numerical value of
is to be regarded as a pure number corresponding to the numerical value of![]() .
.
Note in this respect that the electric charge e, so far not yet explicitly introduced, appears in the model via![]() . This introductory reasoning outlines the next task to be concerned just now: to show how the Equation (4.9) implies the electromagnetic interaction too. This subsection links therefore the following considerations to the Section 7. Usually e is introduced by postulating the Coulomb force; here instead e and thus the electromagnetic forces are introduced starting from
. This introductory reasoning outlines the next task to be concerned just now: to show how the Equation (4.9) implies the electromagnetic interaction too. This subsection links therefore the following considerations to the Section 7. Usually e is introduced by postulating the Coulomb force; here instead e and thus the electromagnetic forces are introduced starting from![]() . By analogy with (8.6), the Equation (8.2) is rewritten as follows
. By analogy with (8.6), the Equation (8.2) is rewritten as follows
![]() (8.18)
(8.18)
i.e. the physical meaning of ![]() introduces itself also the long range Coulomb force component
introduces itself also the long range Coulomb force component![]() .
.
Is evident the formal analogy between ![]() of (8.11), concerning the mass linear density
of (8.11), concerning the mass linear density![]() , and
, and ![]() of (8.18), introducing the charge linear density
of (8.18), introducing the charge linear density![]() : both regard in particular
: both regard in particular ![]() as constant characterizing the lowest order term (8.6) of the series expansion (6.7). This suggests that the first order approximations of Newton and Coulomb laws should be both deducible from
as constant characterizing the lowest order term (8.6) of the series expansion (6.7). This suggests that the first order approximations of Newton and Coulomb laws should be both deducible from ![]() through a dimensional constant. In effect the connection between G and e via a dimensional proportionality constant is easily proven; indeed
through a dimensional constant. In effect the connection between G and e via a dimensional proportionality constant is easily proven; indeed
![]()
yields numerically
![]()
Of course the signs of the component ![]() correspond to equal or opposite charges defining
correspond to equal or opposite charges defining![]() . Implement first (8.18) for both charges at rest in R; so
. Implement first (8.18) for both charges at rest in R; so
![]() (8.19)
(8.19)
where the subscript stands for “rest”; in this equation there is no explicit reference to v, which from now on denotes the relative motion of the charges. As ![]() is arbitrary,
is arbitrary, ![]() has been included in it, to simplify notations like
has been included in it, to simplify notations like![]() .
.
The second way to implement (8.18) assumes constant the rate v with which moves either charge with respect to the other at rest in R; as according to (2.34)![]() , (8.18) yields
, (8.18) yields
![]() (8.20)
(8.20)
Thus
![]() (8.21)
(8.21)
where the subscript stands for “mobile”, whence
![]() (8.22)
(8.22)
The last equality has introduced the time range ![]() defined in a reference system
defined in a reference system ![]() of the mobile charge moving at rate
of the mobile charge moving at rate ![]() with respect to R; an observer ideally sitting on the moving charge in
with respect to R; an observer ideally sitting on the moving charge in ![]() sees the other charge at rest, as the backwards motion of
sees the other charge at rest, as the backwards motion of ![]() in R balances exactly the forwards motion of the charge. So, in practice (8.22) can be regarded likewise (8.19); obviously (8.22) reduces anyway to (8.19) in particular for
in R balances exactly the forwards motion of the charge. So, in practice (8.22) can be regarded likewise (8.19); obviously (8.22) reduces anyway to (8.19) in particular for![]() . Hence it is possible to write the second equality as
. Hence it is possible to write the second equality as
![]() (8.23)
(8.23)
the first equation emphasizes the link between ![]() in R and
in R and![]() , the second equation also follows directly from (8.21) according to the following chain of elementary steps
, the second equation also follows directly from (8.21) according to the following chain of elementary steps
![]()
Regarding ![]() one finds a “new” quantity called magnetic field already introduced as a final step (7.16) of the reasoning in the section 7. The one dimensional scalar approach followed throughout this paper hides the actual vector character of
one finds a “new” quantity called magnetic field already introduced as a final step (7.16) of the reasoning in the section 7. The one dimensional scalar approach followed throughout this paper hides the actual vector character of ![]() and thus of
and thus of ![]() and
and![]() . Simple considerations allow however to surrogate this missing information acknowledging that
. Simple considerations allow however to surrogate this missing information acknowledging that ![]() and
and ![]() are two different corollaries of a unique information to describe the charge dynamics: both Equations (8.23) follow from different ways of rewriting the unique Equation (8.21), as in effect it is physically sensible. So, to avoid that the energy of a mobile test charge in both fields is counted twice summing separately
are two different corollaries of a unique information to describe the charge dynamics: both Equations (8.23) follow from different ways of rewriting the unique Equation (8.21), as in effect it is physically sensible. So, to avoid that the energy of a mobile test charge in both fields is counted twice summing separately ![]() and
and![]() , it is necessary that the former only performs work on the mobile charge, likewise as in the particular case of charge at rest, whereas the latter doesn’t; the vector properties of these forces follow from these considerations, i.e.
, it is necessary that the former only performs work on the mobile charge, likewise as in the particular case of charge at rest, whereas the latter doesn’t; the vector properties of these forces follow from these considerations, i.e. ![]() and
and ![]() must be such that
must be such that![]() .
.
The third way to handle ![]() concerns the case where v is not constant; owing to (8.20), an additional force term
concerns the case where v is not constant; owing to (8.20), an additional force term ![]() is expected because of the addend
is expected because of the addend ![]() previously omitted in (8.21). This additional term reads
previously omitted in (8.21). This additional term reads
![]()
where the acceleration a of the charge appears as a reciprocal frequency because of the factor![]() . It is possible to extract from this chain of equation the frequency
. It is possible to extract from this chain of equation the frequency ![]() defined by the energy
defined by the energy![]() , i.e.
, i.e.
![]() (8.24)
(8.24)
A fraction ![]() of energy
of energy ![]() is thus converted into and appears as electromagnetic radiation, whose energy
is thus converted into and appears as electromagnetic radiation, whose energy ![]() increases of course with
increases of course with![]() . The fact of having found
. The fact of having found ![]() for
for ![]() means that an accelerated charge implies emission of e.m. radiation. Of course
means that an accelerated charge implies emission of e.m. radiation. Of course ![]() and thus
and thus ![]() for
for ![]() or
or![]() , so even this contribution to the right hand side of (8.20) vanishes for charges at rest. In principle
, so even this contribution to the right hand side of (8.20) vanishes for charges at rest. In principle ![]() prospects the chance of calculating the power irradiated by an accelerated charge regarding appropriately
prospects the chance of calculating the power irradiated by an accelerated charge regarding appropriately ![]() and
and ![]() of (8.24). This chance has been exemplified in section 7 in a more complete and rigorous way via the Maxwell equations.
of (8.24). This chance has been exemplified in section 7 in a more complete and rigorous way via the Maxwell equations.
Is still proven useful here the initial idea of implementing uniquely the early Equations (1.11) and (1.12) without any further physical hint but simply including ![]() among the fundamental constants of Nature.
among the fundamental constants of Nature.
8.5. Quantum Charges
Dividing both sides of the inequality (8.3) by ![]() and next by
and next by ![]() too, one finds
too, one finds
![]() (8.25)
(8.25)
being ![]() an appropriate factor. According to (3.69) and (3.70) this yields also
an appropriate factor. According to (3.69) and (3.70) this yields also
![]() (8.26)
(8.26)
Now the question rises: does ![]() have mere numerical meaning or it actually generalize the concept of usual charge e according to
have mere numerical meaning or it actually generalize the concept of usual charge e according to![]() ? To answer this question consider first some implications of (8.26) based on (3.70). As
? To answer this question consider first some implications of (8.26) based on (3.70). As![]() , where A is an arbitrary area and P pressure, one finds the dimensional relationships
, where A is an arbitrary area and P pressure, one finds the dimensional relationships
![]() (8.27)
(8.27)
the Equations (8.26) imply the rising of a pressure P related to the energy density ![]() due to charged particles enclosed in the volume V. Start thus just from the dimensional identity between pressure and energy density and write
due to charged particles enclosed in the volume V. Start thus just from the dimensional identity between pressure and energy density and write
![]() (8.28)
(8.28)
where ![]() is a proportionality factor necessary to define in general the volume V as a function of A defining the pressure. Owing to the dimensional character of this equation, although P and E have been defined specifically by (8.27) and (8.28), the following reasoning holds in general for any E, i.e. also for atoms, ions, elementary charges and even photons. The second equation yields
is a proportionality factor necessary to define in general the volume V as a function of A defining the pressure. Owing to the dimensional character of this equation, although P and E have been defined specifically by (8.27) and (8.28), the following reasoning holds in general for any E, i.e. also for atoms, ions, elementary charges and even photons. The second equation yields
![]() (8.29)
(8.29)
Consider now that if in V are contained photons or matter, e.g. gas particles, it is possible to implement the wave properties of matter and write
![]() (8.30)
(8.30)
the matter particles are assumed moving at average rate v with De Broglie momentum ![]() and thus frequency
and thus frequency![]() ; for calculation purposes,
; for calculation purposes, ![]() has been rewritten as a function of
has been rewritten as a function of ![]() as indicated here to include also photons. The presence of steady waves in V requires
as indicated here to include also photons. The presence of steady waves in V requires
![]() (8.31)
(8.31)
the first equality is directly deducible from (8.30) that expresses the steadiness condition, i.e. the change of ![]() requires that of
requires that of ![]() as
as ![]() with n integer, the second equality expresses the proportionality between
with n integer, the second equality expresses the proportionality between ![]() and E. So the change of E inside V is related to that of
and E. So the change of E inside V is related to that of ![]() of the matter/light waves propagating in V. Implement now the idea that (8.29) regards a number of corpuscles inside V, whose change of energy density is uniquely definable by
of the matter/light waves propagating in V. Implement now the idea that (8.29) regards a number of corpuscles inside V, whose change of energy density is uniquely definable by ![]() anyhow it might be obtained; instead (8.31) regards waves, whose energy changes are presumably related to how the early V is modified by a given
anyhow it might be obtained; instead (8.31) regards waves, whose energy changes are presumably related to how the early V is modified by a given ![]() because of steadiness condition. Reasonably the steady propagation of waves is different depending on whether one side only or two sides or even three sides of V are modified. Consider thus the three possible ways to deform the initial V, whose
because of steadiness condition. Reasonably the steady propagation of waves is different depending on whether one side only or two sides or even three sides of V are modified. Consider thus the three possible ways to deform the initial V, whose ![]() remains however uniquely defined in all cases: V can be equivalently rewritten as
remains however uniquely defined in all cases: V can be equivalently rewritten as ![]() or
or ![]() or
or![]() . Being both
. Being both ![]() and the constant
and the constant ![]() arbitrary, it is certainly possible to define them in order to fit a given value V of course arbitrary itself. Hence
arbitrary, it is certainly possible to define them in order to fit a given value V of course arbitrary itself. Hence
![]()
To make consistent both ways of defining ![]() merge this result with (8.31) to obtain
merge this result with (8.31) to obtain
![]()
whence
![]() (8.32)
(8.32)
Assume that the left hand side defines an average force such that![]() ; dividing both sides by the surface
; dividing both sides by the surface ![]() one finds
one finds
![]() (8.33)
(8.33)
At the right hand side appears an energy density ![]() defined by an amount of energy
defined by an amount of energy![]() , arbitrary, in the volume
, arbitrary, in the volume![]() , arbitrary as well, and recall the initial position (8.28); then, as the dimensions of
, arbitrary as well, and recall the initial position (8.28); then, as the dimensions of ![]() and
and ![]() are force and surface, one finds eventually
are force and surface, one finds eventually
![]() (8.34)
(8.34)
The minus sign in (8.33) and (8.34) has been omitted, it simply establishes whether an internal or external pressure expands or shrinks V. These results, which hold for photons or gases because no specific hypothesis has been made, are well known: ![]() holds for a light beam completely absorbed by the internal surface of V, whereas
holds for a light beam completely absorbed by the internal surface of V, whereas ![]() when waves or corpuscles bounce elastically;
when waves or corpuscles bounce elastically; ![]() yields the well known law
yields the well known law![]() . As
. As ![]() is due itself to elastic shocks of corpuscles against the internal walls of V, then
is due itself to elastic shocks of corpuscles against the internal walls of V, then![]() ; i.e. E should be 2/3 of another energy
; i.e. E should be 2/3 of another energy ![]() that yields
that yields![]() ; is evident the connection of this last conclusion with the elementary kinetic theory of gases, where
; is evident the connection of this last conclusion with the elementary kinetic theory of gases, where ![]() is easily demonstrable to be the average kinetic energy of molecules.
is easily demonstrable to be the average kinetic energy of molecules.
Skipping further considerations on this well known topic, return now to the Equations (8.25) and (8.26) to specify the result (8.34) in order to explain ![]() in the equation
in the equation![]() . The comparison of (8.32) and (8.26) suggests the correspondences
. The comparison of (8.32) and (8.26) suggests the correspondences
![]() (8.35)
(8.35)
where the third position is the usual definition of force. So, owing to (8.26) and (8.18),
![]()
the third equation makes (8.33) compliant with (8.35). So the Equation (8.32) reads
![]() (8.36)
(8.36)
whence, recalling the second (8.26), i.e.
![]() (8.37)
(8.37)
The second and third charges are consistent with quark charges, all with both signs correspondingly to![]() , in the nuclear volume V. It is amazing the fact that even the quark charges appear here as a consequence of the dual wave/corpuscle behavior of matter and light, whereas their fractional character is reminiscent of the radiation/matter wave pressure in the volume enclosing them.
, in the nuclear volume V. It is amazing the fact that even the quark charges appear here as a consequence of the dual wave/corpuscle behavior of matter and light, whereas their fractional character is reminiscent of the radiation/matter wave pressure in the volume enclosing them.
As a final remark, note that all charges can take both signs because e can be found in negative and positive energy states, as previously shown.
Now let us return to (8.24), to exemplify in a simple case how it is in fact calculable.
Let ![]() be the energy of a charged particle; (8.24) provides in principle the energy radiated per unit time with the help of (2.28)
be the energy of a charged particle; (8.24) provides in principle the energy radiated per unit time with the help of (2.28)
![]()
It is easy to find the total power radiated ![]() by such an accelerated particle, knowing that its charge is e and the change rate of its momentum is
by such an accelerated particle, knowing that its charge is e and the change rate of its momentum is![]() . To solve this problem, however, more information is necessary about the link between radiation pressure and energy density. Once having found
. To solve this problem, however, more information is necessary about the link between radiation pressure and energy density. Once having found
![]()
being ![]() the wave frequency, the non relativistic result as a function of the acceleration
the wave frequency, the non relativistic result as a function of the acceleration ![]() is obtained after having multiplied both sides by
is obtained after having multiplied both sides by ![]() via the following chain of equations
via the following chain of equations
![]() (8.38)
(8.38)
8.6. Short Range Nuclear Interactions
The Equations (3.12) and (8.4) suggest specific orders of magnitude significant to introduce short range forces. Skipping all theoretical details outside the purposes of the present paper, a few short comments are exposed below to highlight at least the essential features of these forces implementing only results so far obtained. Consider thus the following chances introduced by the general Equation (8.1)
![]()
to infer, in agreement with (3.14) and the reasons therein explained,
![]() (8.39)
(8.39)
only in the first case ![]() has been replaced by
has been replaced by![]() . The question that rises now is whether these expressions are mere equivalent ways of rewriting the same Equation (8.19) or they represent actually different force laws.
. The question that rises now is whether these expressions are mere equivalent ways of rewriting the same Equation (8.19) or they represent actually different force laws.
Preliminary inspection evidences that in both cases the force is defined via ![]() but in two different ways:
but in two different ways: ![]() depends explicitly on v and
depends explicitly on v and![]() , whereas
, whereas ![]() on
on ![]() only. In the former case the interaction force is inversely proportional to
only. In the former case the interaction force is inversely proportional to![]() ; in the latter case the interaction energy
; in the latter case the interaction energy ![]() increases with the distance
increases with the distance![]() , whatever this latter might be. This suggests the concept of “asymptotic freedom”. Moreover the messenger particles of
, whatever this latter might be. This suggests the concept of “asymptotic freedom”. Moreover the messenger particles of ![]() carrying the interaction through
carrying the interaction through ![]() should be massive, owing to v; the messenger particles of
should be massive, owing to v; the messenger particles of ![]() should be massless, as the force carried through
should be massless, as the force carried through ![]() involves c only. Consequently, one expects that for assigned
involves c only. Consequently, one expects that for assigned ![]() the characteristic range measured by
the characteristic range measured by ![]() is greater than
is greater than![]() .
.
Taking according to (8.4) ![]() and
and![]() , order of magnitude estimates of space ranges and time ranges that characterize
, order of magnitude estimates of space ranges and time ranges that characterize ![]() and
and ![]() can be calculated utilizing the values (3.12). Particularly interesting is in this respect the range
can be calculated utilizing the values (3.12). Particularly interesting is in this respect the range
![]()
1) Consider first ![]() assuming preliminarily that the concerned interactions occur at the nuclear or sub-nuclear scale: i.e. reasonably
assuming preliminarily that the concerned interactions occur at the nuclear or sub-nuclear scale: i.e. reasonably ![]() concerns the interaction between different nucleons and in the nucleons themselves. Accordingly define the length
concerns the interaction between different nucleons and in the nucleons themselves. Accordingly define the length
![]()
which is clearly an average value within![]() , and introduce two complementary subranges
, and introduce two complementary subranges ![]() and
and ![]() of the whole
of the whole ![]() as follows
as follows
![]() (8.40)
(8.40)
It yields
![]()
moreover both subranges expressible through electron and nuclear range sizes yield
![]() (8.41)
(8.41)
Is relevant the fact that that ![]() is surprisingly close to the nucleon Compton lengths
is surprisingly close to the nucleon Compton lengths ![]() of both proton and neutron, which have in effect a similar order of magnitude. Also
of both proton and neutron, which have in effect a similar order of magnitude. Also ![]() does so, which means that the nucleon mass represents the boundary value discriminating the interaction lengths
does so, which means that the nucleon mass represents the boundary value discriminating the interaction lengths ![]() and
and ![]() inside and outside the respective nucleon; this also explains the order of magnitude of the nucleon mass, indeed
inside and outside the respective nucleon; this also explains the order of magnitude of the nucleon mass, indeed ![]() differs from the experimental nucleon mass by about 5.5% only. Here we take advantage of the fact that proton and neutron masses differ by less that 0.14% only. Hence the forces (8.4) defined by these ranges could concern both nucleons and their mutual interactions at distances consistent with the inequality (8.3); indeed, as expected,
differs from the experimental nucleon mass by about 5.5% only. Here we take advantage of the fact that proton and neutron masses differ by less that 0.14% only. Hence the forces (8.4) defined by these ranges could concern both nucleons and their mutual interactions at distances consistent with the inequality (8.3); indeed, as expected, ![]() is related just to the order of magnitude of the nucleon mass, whereas
is related just to the order of magnitude of the nucleon mass, whereas ![]() is related to the binding energy between nucleons. In fact
is related to the binding energy between nucleons. In fact ![]() is attractive, in agreement with the concept of “asymptotic freedom” already emphasized for quarks in nucleons less than
is attractive, in agreement with the concept of “asymptotic freedom” already emphasized for quarks in nucleons less than ![]() apart. The characteristic times are
apart. The characteristic times are ![]() and
and![]() . At this point it is possible a rough estimate of the stability of the nucleus comparing this energy
. At this point it is possible a rough estimate of the stability of the nucleus comparing this energy ![]() with the Coulomb repulsion energy calculated via (8.23) approximately as
with the Coulomb repulsion energy calculated via (8.23) approximately as ![]() between two protons
between two protons ![]() apart;
apart; ![]() is negligible with respect to the attractive field in
is negligible with respect to the attractive field in![]() . The fact that
. The fact that ![]() suggests that
suggests that ![]() should concern sub-nuclear particles that form protons and neutrons, which therefore are not elementary particles themselves. Hence the whole charge of proton and the null charge of the neutron can be due to nothing else but appropriate combinations of the
should concern sub-nuclear particles that form protons and neutrons, which therefore are not elementary particles themselves. Hence the whole charge of proton and the null charge of the neutron can be due to nothing else but appropriate combinations of the ![]() fractional charges (8.37).
fractional charges (8.37).
These considerations, well known and here shortly sketched only, are enough to conclude that ![]() concerns the strong force. Further considerations are clearly outside the scopes of the present paper, merely aimed to show how to identify the fingerprints of the short range forces (8.39) in the conceptual frame hitherto outlined. Some more details are reported in [20] .
concerns the strong force. Further considerations are clearly outside the scopes of the present paper, merely aimed to show how to identify the fingerprints of the short range forces (8.39) in the conceptual frame hitherto outlined. Some more details are reported in [20] .
2) Consider now![]() , noting that with the help of (2.28) the second Equation (8.39) reads also
, noting that with the help of (2.28) the second Equation (8.39) reads also
![]() (8.42)
(8.42)
Being ![]() one expects
one expects![]() ; in other words, once having fixed
; in other words, once having fixed![]() , a shorter interaction rang
, a shorter interaction rang ![]() is to be expected for
is to be expected for ![]() of
of![]() . According to (8.4),
. According to (8.4), ![]() implies information about
implies information about ![]() compatible with
compatible with ![]() in this case. To estimate v in the same reference system of (8.23), implement (8.23) supposing that an appropriate
in this case. To estimate v in the same reference system of (8.23), implement (8.23) supposing that an appropriate ![]() fulfills the condition
fulfills the condition
![]() (8.43)
(8.43)
Elementary manipulations show that this position yields ![]() i.e.
i.e.![]() , whence the solutions
, whence the solutions ![]() and
and![]() . Hence, taking the same value of
. Hence, taking the same value of ![]() of (8.41) by comparison purposes, one finds two possible corresponding ranges
of (8.41) by comparison purposes, one finds two possible corresponding ranges
![]() (8.44)
(8.44)
In effect, extending the Equations (3.12) to the fourth power of ![]() one finds the further length
one finds the further length ![]() necessary to include
necessary to include ![]() in the whole range of
in the whole range of![]() . The first and second results are acceptable, as both yield space ranges shorter than that of both (8.41); the first value, in particular, yields according to the fourth (8.4)
. The first and second results are acceptable, as both yield space ranges shorter than that of both (8.41); the first value, in particular, yields according to the fourth (8.4)
![]() (8.45)
(8.45)
The existence of two range sizes (8.44) of ![]() compatible with (8.43) suggests that
compatible with (8.43) suggests that ![]() should imply two different kinds of massive force carriers, reasonably with and without charges; if so, then the charges must have opposite signs. This kind of interaction needs thus three kinds of carriers. Assuming charged and neutral carriers of masses
should imply two different kinds of massive force carriers, reasonably with and without charges; if so, then the charges must have opposite signs. This kind of interaction needs thus three kinds of carriers. Assuming charged and neutral carriers of masses ![]() and
and![]() , just a few considerations are enough to infer significant information on the masses of these messengers.
, just a few considerations are enough to infer significant information on the masses of these messengers.
Implementing this assumption to establish the energy balance governing the formation of the carriers, the results are in full agreement with the experimental data.
Is reasonable the idea of regarding the cluster of messengers as a system of particles interacting themselves in order that the gain of binding energy of the charges accounts not only for their own masses ![]() and
and ![]() but also for that of
but also for that of![]() . Is interesting the energy balance of the charged carriers according to the electromagnetic Equation (8.43). Start with the energy of a Coulomb system with a nucleus of mass
. Is interesting the energy balance of the charged carriers according to the electromagnetic Equation (8.43). Start with the energy of a Coulomb system with a nucleus of mass ![]() formed by either charge, e.g.
formed by either charge, e.g.![]() , in the field of which interacts the other charge, e.g.
, in the field of which interacts the other charge, e.g.![]() , at average distance
, at average distance![]() ; the subscript “B” stands for “bound”, whereas the simplest hypothesis on the masses is
; the subscript “B” stands for “bound”, whereas the simplest hypothesis on the masses is![]() . Consider preliminarily that such a system can be described as shown in subsection 3.2: the reasoning introduced to describe the electron charge around the nuclear charge holds in principle also for integer spin charged particles. The early hydrogenlike atom was introduced before the concept of spin, which became essential to account for the electron pile up in many electron atoms [7] according to the exclusion principle and for the possible presence of an external field. The success of Bohr’s idea was allowed by the fact that the spin-orbit and spin-spin interaction between electron and nucleus are both small with respect to the Coulomb interaction. Consider at this point uniquely (3.1) that has general validity and skips, as shown in section 3.3, the operator formalism implementing wave functions along with all related implications: e.g. it is known that a 0 spin particle requires a 4 dimensional scalar wave function, whereas a spin 1 particles requires a three component wave function. On the one hand (3.1) has 4 dimensional character as it merges space and time coordinates through the respective uncertainty ranges, to which are related energy and momentum ranges too. On the other hand the necessity of describing the particle in any reference system is in fact ensured by (3.1) according to (3.2). Implement thus the electromagnetic interaction only to describe via (3.1) even a system of spin 1 charged bosons
. Consider preliminarily that such a system can be described as shown in subsection 3.2: the reasoning introduced to describe the electron charge around the nuclear charge holds in principle also for integer spin charged particles. The early hydrogenlike atom was introduced before the concept of spin, which became essential to account for the electron pile up in many electron atoms [7] according to the exclusion principle and for the possible presence of an external field. The success of Bohr’s idea was allowed by the fact that the spin-orbit and spin-spin interaction between electron and nucleus are both small with respect to the Coulomb interaction. Consider at this point uniquely (3.1) that has general validity and skips, as shown in section 3.3, the operator formalism implementing wave functions along with all related implications: e.g. it is known that a 0 spin particle requires a 4 dimensional scalar wave function, whereas a spin 1 particles requires a three component wave function. On the one hand (3.1) has 4 dimensional character as it merges space and time coordinates through the respective uncertainty ranges, to which are related energy and momentum ranges too. On the other hand the necessity of describing the particle in any reference system is in fact ensured by (3.1) according to (3.2). Implement thus the electromagnetic interaction only to describe via (3.1) even a system of spin 1 charged bosons ![]() and
and ![]() trusting that the steps from (3.3) to (3.9) still hold at least approximately also now; the comparison with the experimental data will be the decisive benchmark to assess the validity of these considerations. So it is possible to write for the system of boson charges
trusting that the steps from (3.3) to (3.9) still hold at least approximately also now; the comparison with the experimental data will be the decisive benchmark to assess the validity of these considerations. So it is possible to write for the system of boson charges![]() , see Equation (3.7) with
, see Equation (3.7) with![]() , where
, where ![]() is the reduced mass of the concerned system. Accordingly (3.9) yields
is the reduced mass of the concerned system. Accordingly (3.9) yields
![]() (8.46)
(8.46)
for charges of equal mass. Putting ![]() and including
and including ![]() into
into![]() , this equation reads
, this equation reads
![]() (8.47)
(8.47)
with these positions ![]() depends explicitly on
depends explicitly on ![]() and
and ![]() only, no longer on
only, no longer on ![]() and
and![]() . Is of interest now an appropriate
. Is of interest now an appropriate ![]() compliant with
compliant with ![]() and such that
and such that
![]() (8.48)
(8.48)
with ![]() integer, the second equation is a well known condition of the wave mechanics already implemented in (3.8) with the same physical meaning. Let the shortest wavelength
integer, the second equation is a well known condition of the wave mechanics already implemented in (3.8) with the same physical meaning. Let the shortest wavelength ![]() be the Compton length of either
be the Compton length of either![]() , as suggested by the Equation (3.6) and [7] , i.e.
, as suggested by the Equation (3.6) and [7] , i.e.
![]()
then, replacing ![]() into (8.48) one finds
into (8.48) one finds
![]()
In conclusion, comparing with (8.48) and putting![]() , it is possible to write
, it is possible to write
![]()
These results are verifiable by comparison with the experimental masses ![]() and
and![]() :
:
![]()
which in effect compare well with ![]() and
and ![]() respectively.
respectively.
Moreover note that (8.47) regards by definition ![]() as average distance between
as average distance between ![]() and
and![]() , whereas
, whereas ![]() of (8.44) is by definition the total range of
of (8.44) is by definition the total range of![]() ; therefore one infers that reasonably
; therefore one infers that reasonably![]() . Hence, according to (8.48),
. Hence, according to (8.48), ![]() is the binding energy gain available to create the masses
is the binding energy gain available to create the masses![]() . In effect one finds that the total energy
. In effect one finds that the total energy ![]() related to
related to ![]() is
is
![]() (8.49)
(8.49)
in agreement with (8.45) and with the experimental masses. The Equations (8.47) and (8.46) differ in fact only formally; once having removed ![]() merely including it in the reduced mass of the system as a numerical scale factor, someway analogous to (3.12), it appears that
merely including it in the reduced mass of the system as a numerical scale factor, someway analogous to (3.12), it appears that ![]() is different from but closely related to the electromagnetic interaction constant via the linked energy scale factor.
is different from but closely related to the electromagnetic interaction constant via the linked energy scale factor.
In effect, considering ![]() and
and![]() , and not
, and not ![]() and
and![]() , one calculates experimental masses of the force carriers and reasonable estimate of the interaction range
, one calculates experimental masses of the force carriers and reasonable estimate of the interaction range ![]() that agree with the total energy (8.45); these values support the idea that a hydrogenlike system bound by electromagnetic interaction via photon carriers turns into a short range interaction system via massive carriers. There appears in this way the link between electromagnetic and weak interactions.
that agree with the total energy (8.45); these values support the idea that a hydrogenlike system bound by electromagnetic interaction via photon carriers turns into a short range interaction system via massive carriers. There appears in this way the link between electromagnetic and weak interactions.
At this point, something else about ![]() can be still inferred to confirm that
can be still inferred to confirm that ![]() corresponds to the weak interaction. Helps in this respect the first (8.4)
corresponds to the weak interaction. Helps in this respect the first (8.4) ![]() that reads
that reads
![]()
whence, with the help of the values (8.44),
![]() (8.50)
(8.50)
this is the Fermi constant characterizing the weak interactions.
This result is more than mere fingerprint of weak interactions; interesting information can be inferred from it expressing appropriately energy and volume inherent this result. Write
![]() (8.51)
(8.51)
the energy ![]() that defines the characteristic Fermi constant has been expressed via Compton length of the characteristic mass
that defines the characteristic Fermi constant has been expressed via Compton length of the characteristic mass ![]() that in turn defines
that in turn defines ![]() too. Hence
too. Hence
![]() (8.52)
(8.52)
It is not surprising that one finds once more the value of total energy of this kind of interaction. Implement now the idea that actually the energy (8.49) is degenerate: it consists of ![]() moving in the field of
moving in the field of ![]() or, identically, from
or, identically, from ![]() moving in the field of
moving in the field of![]() . As both configurations can coexist consistently with the unique reduced mass
. As both configurations can coexist consistently with the unique reduced mass ![]() (8.46) that calculates
(8.46) that calculates ![]() of (8.47), it is reasonable to regard the value (8.49) as the sum of both allowed chances; this means that the total energy refers to the total volume calculated via (8.51), so that each configuration has energy
of (8.47), it is reasonable to regard the value (8.49) as the sum of both allowed chances; this means that the total energy refers to the total volume calculated via (8.51), so that each configuration has energy
![]() (8.53)
(8.53)
Note that this value is also consistent with that inferred through a characteristic range similarly as done in (8.40) and (8.41)
![]() (8.54)
(8.54)
8.7. The Dirac and Lamb Equations
This section generalizes the results of the Section 3.2 obtained implementing the non-relativistic equation![]() . The following considerations show how to describe a relativistic hydrogenlike system replacing the classical position (3.4) with the series expansion
. The following considerations show how to describe a relativistic hydrogenlike system replacing the classical position (3.4) with the series expansion
![]() (8.55)
(8.55)
expressing ![]() as
as ![]() similarly as done in the Equations (8.5) or (8.6). In effect even the term
similarly as done in the Equations (8.5) or (8.6). In effect even the term ![]() of (3.4) can be written as
of (3.4) can be written as ![]() with coefficient
with coefficient![]() ; so (3.4) is actually a particular case of the series (8.55) truncated at the second order. Of course
; so (3.4) is actually a particular case of the series (8.55) truncated at the second order. Of course ![]() is an arbitrary constant length that introduces the energy corresponding to force
is an arbitrary constant length that introduces the energy corresponding to force![]() . Although
. Although ![]() vanishes at the infinity, the arbitrary constant
vanishes at the infinity, the arbitrary constant ![]() accounts for the electron rest mass energy. Hence it is possible to write
accounts for the electron rest mass energy. Hence it is possible to write
![]() (8.56)
(8.56)
being ![]() the radial momentum range conjugate to
the radial momentum range conjugate to![]() . All range boundaries are of course arbitrary. In this way we deliberately waive introducing explicitly radial and angular momenta exploited in section 3.2, but implement directly the fundamental Equation (3.1). Multiply both sides of (8.56) by
. All range boundaries are of course arbitrary. In this way we deliberately waive introducing explicitly radial and angular momenta exploited in section 3.2, but implement directly the fundamental Equation (3.1). Multiply both sides of (8.56) by ![]() so that
so that
![]()
The series truncated at the third order yields
![]()
As the coefficient ![]() has not yet been defined, it is convenient to turn this equation into
has not yet been defined, it is convenient to turn this equation into
![]()
then, dividing both sides by![]() , one finds
, one finds
![]() (8.57)
(8.57)
Next write
![]() (8.58)
(8.58)
so that, subtracting ![]() at both sides, one finds
at both sides, one finds
![]() (8.59)
(8.59)
and then
![]()
According to the first (8.57)![]() ; thus the last equation reads
; thus the last equation reads
![]() (8.60)
(8.60)
Put now
![]() (8.61)
(8.61)
This position has two implications: the first replacing it in (8.57)
![]() (8.62)
(8.62)
and the second replacing in (8.60)
![]() (8.63)
(8.63)
Note that we have introduced four conditions: a and b in (8.59) plus (8.62) and (8.63); the unknowns in these equation are![]() . In principle the system appears solvable.
. In principle the system appears solvable.
Taking the reciprocal of both sides one finds
![]() (8.64)
(8.64)
The notations ![]() and
and ![]() have been introduced to allow that the upper and lower signs in (8.58) and (8.56) are independent each other. Then it is possible that
have been introduced to allow that the upper and lower signs in (8.58) and (8.56) are independent each other. Then it is possible that
![]() (8.65)
(8.65)
or
![]() (8.66)
(8.66)
Subtracting (8.65) from (8.66) with the same sign![]() , one finds
, one finds![]() : this suggests that the left hand side of these equations must have the form
: this suggests that the left hand side of these equations must have the form![]() , so that
, so that
![]()
The minus sign at the left hand side of (8.65) represents binding energy of the electron to the nucleus in ![]() units; the first addend at the right hand side represents the energy gain with respect to that of the free electron in either energy state.
units; the first addend at the right hand side represents the energy gain with respect to that of the free electron in either energy state.
The previous algebraic steps aimed just to find an equation introducing the ratio![]() . In effect this ratio is significant because, according to (8.61), if
. In effect this ratio is significant because, according to (8.61), if ![]() then
then ![]() and thus
and thus ![]() whereas
whereas ![]() becomes constant; this is the limit case of free electron. Indeed
becomes constant; this is the limit case of free electron. Indeed ![]() implies binding energy, since the electron takes random values of radial momentum between
implies binding energy, since the electron takes random values of radial momentum between ![]() and
and ![]() depending on its finite random distance from the nucleus.
depending on its finite random distance from the nucleus.
Examine the result (8.65) putting first![]() : in fact, according to the second (8.57), this occurs putting
: in fact, according to the second (8.57), this occurs putting ![]() and in (8.55) and
and in (8.55) and![]() , i.e. considering the energy
, i.e. considering the energy ![]() only instead of the energy range
only instead of the energy range ![]() (Heisenberg compliant quantum case). Now require that
(Heisenberg compliant quantum case). Now require that
![]() (8.67)
(8.67)
must be compatible with the non-relativistic quantum Equations (3.5) and (3.9); in other words, in (8.67) must somehow appear not only ![]() but also n and
but also n and ![]() as well. To fulfill this boundary condition as a limit case for small values of
as well. To fulfill this boundary condition as a limit case for small values of![]() , put in (8.67))
, put in (8.67))
![]() (8.68)
(8.68)
in effect, replacing and expanding in series around![]() , (8.67) becomes
, (8.67) becomes
![]()
Considering in particular![]() , the boundary condition requires
, the boundary condition requires![]() . Once having identified
. Once having identified![]() , regard then
, regard then ![]() and
and ![]() in order to be compliant with l and
in order to be compliant with l and ![]() of Equation (3.5), while also fulfilling (3.9) and (3.10). This suggests reasonably
of Equation (3.5), while also fulfilling (3.9) and (3.10). This suggests reasonably![]() , being s the electron spin; in effect, depending on the sign,
, being s the electron spin; in effect, depending on the sign, ![]() becomes l or
becomes l or![]() . In conclusion
. In conclusion
![]() (8.69)
(8.69)
This is the Dirac equation, which however becomes in the present approach particular case of an even more general equation including ![]() as well. The Equation (8.65) reads indeed
as well. The Equation (8.65) reads indeed
![]()
which removes the degeneracy of states with equal n and j of the Dirac equation and also suggests that a further physical effect related to ![]() not concerned in (8.69) is still hidden in this result. In effect the Dirac equation becomes in this approach the zero order approximation of a more complex energy function whose series expansion reads
not concerned in (8.69) is still hidden in this result. In effect the Dirac equation becomes in this approach the zero order approximation of a more complex energy function whose series expansion reads
![]() (8.70)
(8.70)
It is evident that (8.70) removes the degeneracy of the ![]() and
and ![]() states: indeed, whatever the actual analytical form of
states: indeed, whatever the actual analytical form of ![]() might be, calculating the energy difference of these states one finds
might be, calculating the energy difference of these states one finds
![]()
Owing to the physical dimensions ![]() of the coefficient
of the coefficient ![]() in the second (8.57), it is easy to guess the order of magnitude of the second addend of
in the second (8.57), it is easy to guess the order of magnitude of the second addend of ![]() according to the following reasonable positions
according to the following reasonable positions
![]()
being ![]() the electron Compton length. So it follows from the second (8.57) with the help of (3.4) and (3.8)
the electron Compton length. So it follows from the second (8.57) with the help of (3.4) and (3.8)
![]() (8.71)
(8.71)
The second addend of ![]() in (8.71) is the signature of the radiative energy displacement due to the interaction of the electron with the quantum vacuum, known as electron driven vacuum polarization effect; the analytical form of the first addend represented by
in (8.71) is the signature of the radiative energy displacement due to the interaction of the electron with the quantum vacuum, known as electron driven vacuum polarization effect; the analytical form of the first addend represented by![]() , not yet concerned explicitly, is at present still under investigation. So, even without detailed calculations in this respect, appear two relevant facts: 1) the first three terms of (8.55) are enough to infer the Dirac equation; 2) the cubic term and the implementation of the energy range
, not yet concerned explicitly, is at present still under investigation. So, even without detailed calculations in this respect, appear two relevant facts: 1) the first three terms of (8.55) are enough to infer the Dirac equation; 2) the cubic term and the implementation of the energy range ![]() instead of a unique energy term
instead of a unique energy term ![]() are essential to infer contextually the Lamb energy shift too.
are essential to infer contextually the Lamb energy shift too.
9. Discussion
The present model has concerned several topics of fundamental physics self-consistently inferred uniquely from the concept of evolution inherent the definitions (1.11) and (1.12). The concepts of mass, momentum, energy and electric charge, obviously missing in these equations, have been uniquely and self-consistently introduced through the fundamental constants of Nature. It appears also significant the chance of describing the Universe according to laws inferred from the change of a unique primordial function![]() , even regardless of a specific and detailed knowledge about the function that is changing itself: it is instead crucial how it changes.
, even regardless of a specific and detailed knowledge about the function that is changing itself: it is instead crucial how it changes.
The fact of having introduced an initial function and its actual space time evolution, has been proven enough to infer contextually quantum uncertainty and relativistic results in a surprisingly straightforward way even regardless of any deterministic metric and without hypotheses “ad hoc”.
On the one side the necessity of quantized physical laws is implied by the concept itself of uncertainty, Equations (3.1) and (3.2), on the other side special and general relativity are implied by the space time frame under the condition of its holistic evolution. The reverse reasoning is also true: the foundation of quantum and relativistic theories are the fingerprint of an evolving Universe, whose evolution is governed by a few constants in which are nested the essential dynamical variables of interest for the everyday experimental activity, mass, energy charges and so on.
The modern physics is essentially wave physics. This is because the Bohr atom first opened the way to the hydrogenlike atoms and thus to the probabilistic interpretation of the wave functions. Next Schrödinger further enhanced this conceptual path including in the wave function the potential term and thus the electron correlation in many electron atoms and ions. Eventually a further step ahead was accomplished by Dirac: with its relativistic hydrogen atom, He has in fact introduced the quantum field theory. Yet all these physical models implemented wave formalism. The present paper, instead, introduces and contextually exploits the corpuscle nature of the particles constituting the matter, appropriately integrated with their wave nature when necessary. The subsection 3.2 has been reported just to clarify this point. In this way is irrelevant the theoretical problem raised by many physicists about why![]() , and not
, and not ![]() itself, has physical meaning [21] ; moreover the approach to the various equations of quantum and relativistic physics appears not only simpler but also the equations themselves are more interconnected. The Heisenberg principle has negative content; the statistical formulation of the space time uncertainty has instead a highly positive content as it shares both quantum and relativistic theories. Regarding a fundamental statement the uncertainty and following the approach shortly sketched in Section 3.2 the EPR paradox would be meaningless because the concept of distance is missing; the uncertainty ranges waive since the beginning conceptually, and not as a sort of approximation useful to simplify calculations, the concepts of local space time coordinates necessary to define “superluminal” distances.
itself, has physical meaning [21] ; moreover the approach to the various equations of quantum and relativistic physics appears not only simpler but also the equations themselves are more interconnected. The Heisenberg principle has negative content; the statistical formulation of the space time uncertainty has instead a highly positive content as it shares both quantum and relativistic theories. Regarding a fundamental statement the uncertainty and following the approach shortly sketched in Section 3.2 the EPR paradox would be meaningless because the concept of distance is missing; the uncertainty ranges waive since the beginning conceptually, and not as a sort of approximation useful to simplify calculations, the concepts of local space time coordinates necessary to define “superluminal” distances.
As concerns the quantum way of describing the reality, these basic concepts can be summarized as follows
![]() (9.1)
(9.1)
The upper part deals with differential equations that by definition describe the local properties of the solution of the pertinent wave equation; the lower part describes instead the system regardless of its local properties and thus without need of solving the pertinent differential equations. In principle both approaches are equivalent, although the operator formalism is a byproduct of the quantum uncertainty; in practice, however, the problem is to see which approach is more effective in describing the quantum properties of the Universe regardless of the local and deterministic tensor formalism. It is worth recalling that all papers based only on the Equation (3.1) only, allowed to obtain the most significant results of both general relativity and quantum physics [20] ; in the latter case, in particular, the usual positions (3.28) introducing the operator formalism of wave mechanics according to (3.66) and (3.67) are systematically replaced by the uncertainty positions
![]() (9.2)
(9.2)
while obtaining results identical to that of the standard wave formalism, as shortly shown in subsection 3.2.
The classical dynamical variables p and ![]() are to be regarded equivalently as quantum differential operators or quantum uncertainty ranges: this implies that actually it is necessary neither to solve the Schrödinger equation of wave mechanics nor the tensor calculus of relativity. The form (3.2) expressing the quantum uncertainty, apparently weird, shows the quantum equivalent of the relativistic covariance: the Equations (3.1) could seem defined in some particular reference system, instead (3.2) show that whenever the dynamical variables are replaced by the respective uncertainty ranges about which nothing is known in the sense highlighted in the subsection 3.2, the dependence of any formula on a particular reference system, inertial or not, is lost. So the independence of formulas on any particular R is ensured by (3.1), despite their different forms in R and
are to be regarded equivalently as quantum differential operators or quantum uncertainty ranges: this implies that actually it is necessary neither to solve the Schrödinger equation of wave mechanics nor the tensor calculus of relativity. The form (3.2) expressing the quantum uncertainty, apparently weird, shows the quantum equivalent of the relativistic covariance: the Equations (3.1) could seem defined in some particular reference system, instead (3.2) show that whenever the dynamical variables are replaced by the respective uncertainty ranges about which nothing is known in the sense highlighted in the subsection 3.2, the dependence of any formula on a particular reference system, inertial or not, is lost. So the independence of formulas on any particular R is ensured by (3.1), despite their different forms in R and![]() ; however holds the more substantial fact the any formula inferred from (3.1) has validity in any
; however holds the more substantial fact the any formula inferred from (3.1) has validity in any![]() : this is the profound reason why relativistic formulas can be inferred from (3.1).
: this is the profound reason why relativistic formulas can be inferred from (3.1).
Yet, the rational foundation of everything is just the conceptual impossibility of knowing everything.
10. Conclusions
As stated in Section 1, part of this paper aimed to find known results as a test of validity of the present theoretical model. Besides well known results, explicitly quoted throughout the exposition, the model has also provided original results:
− Evolutionary imprinting and derivation of physical laws.
− Possible granular structure of the space time.
− Possible quantization of the temperature.
− Lnk between entropy, phase space and space time.
− Link between Van der Waals equation and quantum zero point state of matter.
− Link between relativity and quantum gravity.
− Probabilistic link between corpuscle and wavelike behavior of matter.
− Link between operator and uncertainty driven approach to quantum problems.
− Generalization of Dirac equation to include the Lamb effect.
Moreover:
− The Equations (4.4) and (3.13) show that even a small mass ![]() can take large values of kinetic mass m for
can take large values of kinetic mass m for![]() ; also, (4.6) shows that just m is the classical mass.
; also, (4.6) shows that just m is the classical mass.
− The Equation (6.19) has shown the existence of finite vacuum energy density![]() , to which corresponds according to (8.34) a pressure
, to which corresponds according to (8.34) a pressure![]() .
.
− The Equation (4.7) has shown that the corpuscle/wave behavior of matter has probabilistic character and that this probability involves the ratios ![]() and
and![]() .
.
− The velocity dependence of mass shows that ![]() implies
implies![]() , whatever
, whatever ![]() might itself be; contextually, increasing
might itself be; contextually, increasing ![]() to
to ![]() means decreasing
means decreasing ![]() from c to a smaller value
from c to a smaller value![]() .
.
− Short notes, although necessarily incomplete, emphasize the essential fingerprints of the strong and weak interactions, Equations (8.37), and contextually also the gravity force and Maxwell equations.
− The model explains why un upper limit of velocity, c, must necessarily exist.
These short remarks are enough to conclude that the present model fits the basic concepts of thermodynamics and fundamental forces of nature merging concept of quantum and relativistic physics.
NOTES
*Retired Physicist.