Threshold Parameter for the Control of Unemployment in the Society: Mathematical Model and Analysis ()
1. Introduction
Securing a job or gain employment in our contemporary society is problematic for an average people and below; not to talk of desire job and underemployment is not something to rule out. In reference to Bureau of Labour Statistics defines unemployment as people who do not have a job, have actively looked for work in the past 4 weeks, and are currently available for work but could not get one or people who were temporarily laid off and were waiting to be called back to that job, Kimberly [1]. Galindro and Torress [2] referred to unemployment as a precarious social situation because a proportion of population normally struggles to maintain a minimum welfare and consumption level.
The unemployment is calculated as a percentage by dividing the number of unemployed individuals by all individual currently in labour force. During period of recession, an economy usually experiences a relatively high unemployment rate. According to the International Labour Organization (ILO), more than 200 million people globally or 6% of the work force were without job in 2012.
Economy of every nation is characterized by both active and inactive populations. The economically active ones are referred to as population willing and able to work and include those actively engaged in the production of goods and services and those who are employed, Muogbo and John-Akameli [3].
Nigeria has a challenge of accurate unemployment rates (i.e. data) to access. However according to Oyebade [4], Nigeria unemployment can be grouped into two categories; firstly, the older unemployed who lost their job through redundancy and bankruptcy and secondly, the younger unemployed, most of whom have never been employed. According to Awogbenle and Iwuamadi [5], the statistics from the man power board and the Federal Bureau of Statistics showed that Nigeria has a youth population of millions representing 60% of the total population of the country.
From Figure 1, it could be seen that, rate of unemployed youth has no year of declination in Nigeria despite efforts of Executives at various levels of government and in specific, 2017 N-POWER recruitment programme by President Muhammad Buhari administration. Also, 64 million of the youth are unemployed, while 1.6 million are under employed. The 1990-2000 data on youth unemployments showed that the largest group of unemployment is the secondary school leavers. Furthermore, 40% of the unemployment rate is among urban rural youth and 20 - 24 years old and 31% of the rate is among those aged 15 - 19 years old. Also the two third of the urban employed are rangeing from 15 - 24 years old. Also, the educated unemployed lie among young males with few dependents. There are relatively few secondary school graduates and the lower job
![]()
Figure 1. Trend of unemployment population (National Bureau of Statistics, Nigeria).
expectations of the primary school graduates. The causes of unemployment are heavily debated. Classical economics, new classical economics and the Austrian school of Economics argued that the market mechanisms are the reliable means of resolving means of unemployment; these theories against intervention imposed on the labour market from the outside such as unionization, bureaucratic work rules, minimum wages laws, taxes and other regulations that can claim discourage in the hiring of workers.
The problem of youth unemployment is very evident and severe in Nigeria. Every year, thousands of graduates are turn out for whom there are no jobs to accommodate them. Some are youth hawkers and bike riders who ordinarily would have found gained employment in some enterprises, or would have demonstrated their skills and resourcefulness if there are enabling environment and reliable management structure on ground. Instead, today youth have now shifted attention to cyber crime, terrorism and other criminal acts. It is the large number of youths who are unemployed capable of undermining democratic practices, constitute a serious threat if engaged by a political classes for clandestine activities.
In the study of youth unemployment activities especially in Nigeria, Adebayo [6], Alanana [7], Ayinde [8], Awogbenle and Iwuamadi [5], David and Ugocheckwu [9] have identified the main causes of youth unemployment in Nigeria. The rural-urban migration is one of the causes of unemployment as the rural area is no longer attractive, youth moves to urban areas with the motive of securing lucrative employment in the industries. In addition, is the misconception of social amenities in the urban centres. This mean that the rural areas are poorly consider in the allocation of social and economic opportunities.
Uddin and Osemengbe [10] also proposed a research that looked into the effects and solutions to youth unemployment in Nigeria. The data for their paper was collected from secondary sources using the descriptive approach of previous researchers and analysis of scholars to gather empirical data, their research revealed that unemployment in Nigeria among youths are caused by six major effects leading to communal clashes and the rise of such groups such as Boko Haram, Niger Delta Militant, Armed Robbery, Prostitution and child trafficking constituting hiccups to lifes and properties. Also, there research revealed that unemployment in Nigeria increases from 21.1% in 2010 to 23.9% in 2011 with youth unemployment at over 50% from 2011 to 2013, there is about increament of 16% unemployment growth rate in Nigeria. The impact of their paper also revealed that Government should invest on education heavily so that graduate will be self reliance instead of job seekers.
Another cause of unemployment in Nigeria is rapid growth rate. According tk worldometers, the current population of Nigeria is 196,364,552 as of Saturday 11th August, 2018, which was said to be the latest United Nations estimates while country meters read as of Sunday, 12th August, 2018, Nigeria population to be approximate 197.8 million. With this population, Nigeria is the most populous nation in Africa, the high population has resulted to rapid growth of labour force which is far outstripping the supply of jobs.
About mathematical contribution to knowledge of unemployment and method of analysis include; Pathan and Bhathawala [11] presented and analyzed a mathematical model for unemployment with fours dynamical variable; Unemployment
, Present job
, Vacancies
, and Employed person
. They analyzed the effect of the action of Government and private sector to control unemployment without and with the presence of delay, they also looked into the impact of self employment to decrease unemployment. Their analysis revealed the stability of non negative equilibrium point of the system, as well as numerical simulation for the validity of the analytical results.
Galindro and Torres [2] also proposes a simple mathematical model for unemployment. They worked with two compartmental models and the model was analyzed with real life data from Portugal. An optimal control was also formulated for the model and solved in which the results of their claim show realistic and non trivial solution.
Edogbanya and Ibrahim [12] Mathematical model of poverty and crime in human society. They developed a four compartmental models of poverty, crime, and incarceration using the system of non linear ordinary differential equation, they established the conditions that guarantee the stability of the model at crime free equilibrium and endemic equilibrium, they also determined the basic reproductive number R0 of the model and used it as a threshold condition, they also carried out the sensitivity analysis on the parameters and carry out numerical simulations with respect to the data.
Akinboro et al. [13] presented a paper on Numerical solution on SIR model using Differential transformation method and Variational iterative method. There studies investigated the application of Differential transformation method and variational iteration in finding the approximate solution of (SIR) model. SIR model are nonlinear system of Ordinary Differential Equation that has no analytic solution. The authors used general Lagrange multiplier concept to construct correction functional for VIM in solving the problem and tansformation of the original nonlinear system into numerical scheme called DTM. Their results revealed that both methods are in complete agreement, accurate and efficient for solving system of ODE. Many other authors have used VIM for model analysis and among are [14] [15] [16].
In view of all above, it is obvious that unemployment is one of the identified menace of contemprory society, especially, in Nigeria. To combat this problem, everybody is required to put positive effort and here I propose mathematical model to study the dynamics in population and set threshold to contain the challenge.
2. Mathematical Model Formulation and Analysis
2.1. Mathematical Model Formulation
The deterministic mathematical model was used to study the dynamics of unemployment. Individuals in the population are divided into compartments depending on the status of individual. The total human population at time t denoted by
, is divided into four sub-population of Unemployment
, and Unemployment compartment splitted into active,
and passive,
,
means Employment compartment,
denotes Retired compartment and lastly
represent vacancy/position available for recruitment compartment.
We assumed that there is an invisible interaction among all the human compartments and the vacancy compartment (this is represented with dotted line in the model diagram). The recruitment rate into the passive unemployment compartment is
,
is the recruitment rate into the active unemployment,
is the rate at which individual moves from passive unemployment state,
is the rate at which individual moves from active unemployment, to employment compartment,
is the rate by which individual moves from employment class to retired. It is also assumed that people can still move from retired to both active and passive unemployment and the rate of their movements are denoted respectively by
and
.
is the vacancy creation of the employed people,
and
are the rate at which the employed people become unemployed probably, dissmisal resulting from misconduct or lack of productivity,
are those that dies while working,
is unpublicized available vacancies and
is the natural death rate.
2.1.1. Flow Diagram of the Model
The model flow diagram (Figure 2) is described by the following system of nonlinear differential equations
(1)
(2)
(3)
![]()
Figure 2. Unemployment Model Flow diagram.
(4)
(5)
2.1.2. Assumptions of the Model
1) Only people of average and/or below (in a population) seek for job;
2) It is assumed that some unemployed individuals are not employable, yet, they seek for employment;
3) It is also part of assumption that some employed individuals have an establishment and also recruit from the pool of unemployment;
4) Some retired individuals added or return to unemployment population in either passive or active way;
5) For as long as people retire from job or loosing their job, there will always be vacancy and recruitment except it may not be publicized;
6) Available vacancy is somehow reserve for special people;
7) It is also assumed that the model considered able human being and dynamics of vacant positions; and
8) It is assumed that not everyone in the active compartment is looking for job.
2.2. Model Analysis
2.2.1. Basic Properties of the Model
The validity of any mathematical model depends whether the system of equations has a solution and communicate practical sense. If yes, is the solution unique? This subsection is concerned with examining if the system of equations has a solution(s) and possesses uniqueness, feasibility and positivity of solution properties.
Theorem 2.1.
Let
denote the region
, the system Equations (1)-(5) with initial conditions
,
,
,
and
, exit, bounded, positively invariant and attracting for all
.
Proof.
1) For existence and uniqueness of solution, we show that
,
are continuous and bounded in
.
From (1),
,
,
,
,
From (2),
,
,
,
,
Same approach for the remaining equations and consider
where
(6)
Integrating (6)
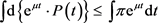
Using initial condition (i.e.
at
), it implies that
(7)
Hence,
is the upper bound of
.
Thus, when
, the solution of
is bounded in the region of
.
Clearly, the partial derivatives of the whole system of equations exists, finite and bounded.
2) For feasibility region of solution
Let
Therefore,
and conclude that
is the feasible region.
3) For positivity of solution, from the proposition of the theorem, initial condition of the system is
, then, we show that the solution set
of the system remain non-negative for all
Integrating both side
Also,
Similarly,
By deducation,
Hence, for
, all the state variables are non-negative. And this completes the proof.
2.2.2. Existence of Equilibria Points
We proceed to investigate the equilibrium points for the model, at equilibrium Equations (1)-(5) become
(8)
(9)
(10)
(11)
(12)
In the absent of recruitment,
,
, to have
Therefore, the absent of recruitment equilibrium (
) is obtained as
(13)
And persistent recruitment equilibrium, we assume
, solving for the remaining variables, we get
,
,
, 1,
.
Therefore the equilibrium of persistent recruitment denoted by
obtained as
(14)
2.2.3. Threshold for the Recruitment
To examine the local stability of
given by (13), is is imperative to obtain threshold parameter called basic reproduction number (
) in the sense of epidemiology, which is defined as the average number of secondary infections caused by a typical infectious individual during its period of infectiousness in a completely susceptible population, (Samson et al., [17], Mastahun and Abdurahman, [18], Getachew et al., [19], Gabriel et al., [20] ). However, in this context, (
) is referred to as the threshold for the recruitment into unemployed population.
We consider only the Employment and Retired compartments and with approach of next generation matrix (NGM)
For which recruitment matrix (F) and transition matrix (V) respectively deduced as
and
to obtain threshold for recruitment, which is the spectral radius of the NGM, written mathematically as
(15)
is the parameter that governs unemployment pool. When
; the situation for which the vacancy and employment population is more than unemployed individuals and it is closely observed. Otherwise, the economy of such soceity will greatly be affected.
2.2.4. Stability Analysis of the Model
Here, we carry out the steady states analysis; Absent of Recruitment steady state and the Persistent Recruitment steady state.
Therorem 2.2.
In the absence of recruitment equilibrium point, Equations (1)-(5) is locally stable if
and unstable if otherwise.
Proof.
To check for the stability analysis of the recruitment free equilibrium of the model, we have to obtain the Jacobian matrix of the given Equations (1)-(5) as follow
(16)
(17)
Solving the above expression to obtain values for the λ’s, we have;
(18)
Condition for stability is that, all eigenvalues of the Jacobian matrix must be less than zero [20]. Hence,
require to be less than zero (i.e. removal rate to employment must be greater than recruitment rate to unemployment) for stability.
Conversely, if
, then, the case employment free equilibrium will be unstable and further analysis would be required, which it not the interest of this research.
2.2.5. Application of Variational Iteration Method (VIM)
Applying the Semi-analytic Numerical Scheme; VIM and employ concept used in [13] for the correctional functionals on our model as:
(19)
it is shown from Akinboro et al., [13] that
,
,
,
,
, substituting the multipliers into the correctional functional above, then, we have the following iterative formula
(20)
3. Numerical Simulation and Discussion of Results
3.1. Numerical Simulation
Implementing (20) on maple 18 with initial conditions
and
and values in Table 1, the following infinite series solutions were obtained for K = 4.
(21)
3.2. Discussion of Results
This article recorded the following findings:
・ When there is no employment, it is practically sensible that there would be no retirement but vacancy exists due to active unemployment and may/maynot be publicize, Equation (13).
・ As employment exist, the result obtained illustrates retirement, vacancies and population of unemployment (both passive and active), all exist, Equation (14).
・ A threshold that is to establsih stability of unemployment was obtained and required to be well manage, Equation (15). When
, implies people getting job are more than those without job, otherwise, the economy of such community will face hardish.
・ It could be seen that all eigenvalues of the characteristics equation give expression less than zero except
, which for stability, must be less than zero and this said
is the threshold (implies the assurance of resolving problem of unemployment in contemporal world depends on the threshold) obtained for unemployment, see Equation (18). This is in support of result obtained is (15) and it importance.
・ VIM was employed to obtain an approximate solution of the propose model and the solution was hypothetically fitted with values to produce results in Table 2, which shows how the population behaves as time goes by. Starting from year 1 to year 5. At first year, it showed that the available vacancies is not in proportion with the available population and it is practically sensible that, out of the total population of unemployment in the first year, almost half of the population are get employed, which showed that the remaining unemployed individuals added up to the next year population and that is why the population of unemployment keep rising as time goes.
4. Summary, Conclusion and Recommendations
4.1. Summary
Here is summary of the research carried out on mathematical modeling of unemployment with retirement and conclusion made based on our findings.
![]()
Table 1. Definition of parameters and Simulation value.
![]()
Table 2. The model solution obtained by V.I.M. was arbitrarily truncated and hypothetically fitted to observe the population of the dynamical model.
In this research, we are able to modify the model of [2] features the dynamics of unemployment with consideration of retirement. We established the existence and uniqueness of solution of the model. The assurance of resolving problem of unemployment in the population was also, achieved. We further obtained the threshold that must be met in order for stability of the unemployment population. The last is the use of VIM to validate the analytic solutions of the model. A radical behaviour of the model was observed if quick intervention is not surface.
4.2. Conclusions
The cooperate environment is now very dependent on skills and technical know-how, western education and certificate(s) is/are no longer enough/unenthusiastic to provide food on the table. Hence, this article concluded that:
1) Every individual have contribution to end unemployment by developing self skills of entrepreneur or learn one (this can be view from Equation (13)).
2) Important threshold (see Equation (15)) to curtail challenges of unemployment was established and beseeched government and policy makers to introduce policy/strategy in proportion to exponential population growth.
3) It is imperative for the employed individuals to prepare for retirement as pension scheme is not sufficient to cater for life after 35years of service (Equation (18)).
4.3. Suggestion for Further Research
This article studied dynamics in mathematical sense, unemployment and established important parameter, called threshold, unemployment is said to be stable for
(when no recruitment except active unemployed created job) and
will also stable when there is employment (i.e. when everybody put effort and create job) but we did not consider the case
, which could be refered to as bifurcation analysis in the mathematical view (when total number of vacant position is equal to number of population). Also, the model can be modified based on asumptions different from those here considered.