1. Introduction
Covering nearly 327,000 ha [1] [2] to 340,300 ha (according to the map by [3] ), the Malagasy mangroves belong to the Indo-Pacific region [4] . Recent evaluations by [5] shed light on these spatial uncertainties by advancing the figure of 213,000 ha of remaining mangroves for the entire Big Island, representing 2% of global mangroves [6] [7] . Those of Madagascar are poor in floristic diversity: only 5 Mangrove families, according to [2] , and 9 characteristic species of East Africa, according to [8] . 98% of the Malagasy mangroves are located on the West coast of Madagascar [7] [9] [10] [11] .
According to [5] , Madagascar lost 57,359 ha of its mangroves, which is 21% of their total area between 1990 and 2010, and this with an annual deforestation rate of 1.06%. This spatial loss follows the global trend described by [12] [13] [14] that Malagasy mangroves are degraded due to anthropogenic and natural pressures. Reactions to this degradation, various forms of preservation such as REDD+ and the financial valuation of carbon from Mangroves are proposed by various authors, despite the associated challenges [14] [15] [16] [17] . To do this, knowledge of the carbon sequestration potential of a Mangrove is unavoidable, and as a corollary, it is important to know the amount of biomass produced in the roots, leaves, stems, as well as through the different aerial and underground compartments of the plant.
Very few reliable scientific data exist on Malagasy mangroves [18] . Apart from the remote sensing work undertaken by [19] in the region, mangroves in the Mangoky Delta remain unexplored and much effort is still needed in ecological diagnosis [11] . Data on their productivity are lacking [11] despite current national and international concerns for the sound management of coastal resources. No baseline study on specific tools for biomass modeling exists for the country and the use of allometric equations developed elsewhere remains for the moment the only way to know the biomass potential of Malagasy Mangroves in general and those of Mangoky Delta in particular. Having confirmed this gap on the East African Mangrove ecosystem, [20] has studied the Rhizophora mucronata Lam (Rhizophoraceae) biomass in Gazi Bay [21] ; for their part, advanced allometric relationships for the estimation of the aboveground biomass of this same species, still in Gazi. [22] has studied the Bruguiera gymnorhiza (L.) Lamk Mangrove biomass in South Africa. Thus, the formula developed by these authors, as well as those advanced by [23] [24] [25] [26] , and recently by [21] are the main reference available for the aboveground biomass estimation of the Kenyan and Eastern African R. mucronata [27] . However, the global basic equations established by [28] and [29] remain benchmarks, in spite of the possible stationary and structural differences between the Malagasy Mangroves and those of other countries.
To compensate for these shortcomings, the present article tries to provide quantitative data on the aerial phytomass of the two species characteristic of the Mangoky Delta, namely Avicennia marina Vierh. (Avicenniaceae) and Rhizophora mucronata. It tries to establish allometric relationships between the aboveground biomass, the diameter at breast height, and the total height and basal circumference of trees. The mathematical models thus established will constitute specific tools for the practical estimation of the production potential in aboveground biomasses of the two Mangrove species of the Mangoky Delta―SW Madagascar.
2. Materials and Methods
2.1. The Study Area
Located on the South-West coast of Madagascar, the study area concerns the Mangoky Delta (Figure 1). Crossed by the Mangoky River, it lies between 43˚26' and 43˚44' East longitude, 21˚15' and 21˚35' South latitude. With decreasing precipitations of 600 to 400 mm per year from North to South, its climate is dry, which can even be described as semi-arid in the boreal part of the delta. The average annual temperature of the Mangoky Delta oscillates between 24.3˚C and 24.9˚C, with a high annual evapotranspiration of 455 to 755 mm, and a high annual insolation of 3551 to 3724 hours. With a tidal range of about 3 m, the delta comprises 11,790 ha of mangrove, according to satellite images of 2000 [11] [30] .
2.2. Quantification of Aerial Phytomass
Forty-three trees (23 Rhizophora mucronata and 20 Avicennia marina) were selected and fell to the ground on October 2009. These operations were preceded by a floristic inventory of the trees, which was carried out in four 100 m linear transects (Figure 1), arranged randomly and perpendicular to the stream lines, each containing ten plots of 10 m × 10 m. For each of the two species studied, the selection of trees was made on the basis of diameter at breast height (DBH at 1.30 m; Table 1), with five to eight individuals per diameter class of 5 cm. The trees for which the DBH was less than 5 cm were not selected [11] [30] . It should be noted that in addition to the pre-identification of in situ species, using some morphological identification keys of the leaves, roots, stems, flowers and fruits, herbarium collections were collected on site in order to confirm real scientific names of the trees at the Botanical Laboratory of Tsimbazaza in Antananarivo.
After felling the trees, the following main dendrometric parameters were measured on the site itself:
- Height of the stem “Hf”;
- Height of the crown “Hh”;
- Total height of the tree “Ht = Hf + Hh”;
- Width of the crown “Lh”;
- Circumference of the stem at the base, on the ground “Cb”;
- Diameter of the tree at 1.30 m from the ground “DBH”.
The entire aerial part of each tree was weighed on site, distinguishing foliage, boughs (less than 2 cm in diameter), branches (woody part of more than 2 cm in diameter located above first branch) and the stem (woody part below the first branch). The weight of hard wood (whole stem and branches) was calculated.
![]()
Figure 1. Location of the study site (Mangoky Delta―SW Madagascar).
![]()
Table 1. Number of trees felled during sampling.
The aerial roots of Rhizophora mucronata were also weighed. The fruits and the flowers, not very abundant on the felled trees, were not taken into account. For each tree and for each compartment, samples were taken, weighed and placed in an oven (105˚C) during 72 hours, and this, in order to deduce the weight of dry phytomass.
2.3. Mathematical Modeling of Dry Biomass
The modeling of the dry biomass of felled trees was carried out from the logarithmic equation:
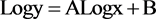 (1)
(1)
or whether:
 (2)
(2)
where y represents dry biomass, x a variable defined from the measured dimensions of the tree such as DBH, (DBH)2∙Ht and Cb.
The linearity of established logarithmic regressions was verified from the correlation coefficient R2, which is considered significant from 0.9.
3. Results
3.1. Structures and Aboveground Biomass
At least 6 species of Mangrove are present in the studied delta: Avicennia marina, Xylocarpus granatum Koen. (Meliaceae), Ceriops tagal C. B. Rob. (Rhizophoraceae), Rhizophora mucronata, Bruguiera gymnorhiza, and Sonneratia alba. The average height of trees varies from 8.3 to 9.2 m, respectively for the facies with A. marina and R. mucronata. Their average diameter is 14 cm (with a minimum of 6.37 cm and a maximum of 23.57 cm) for the first and 15 cm (with a minimum of 6.05 cm and a maximum of 21.34 cm) for the second.
The total above ground biomass varies between 9 and 235 kg per tree for Avicennia marina. It is from 11 to 360 kg for Rhizophora mucronata. The arithmetic averages obtained are respectively around 110 kg and 173 kg per tree for both species (Table 2 and Table 3).
![]()
Table 2. Partial and total dry aerial phytomass of Avicennia marina (Hf: Height of the stem; Hh: Height of the crown; Ht = Hf + Hh = Total height of the tree; Lh: Width of the crown; Cb: Circumference of the stem at the base; DBH: Diameter of the tree at 1.30 m from the ground).
![]()
Table 3. Partial and total dry aerial phytomass of Rhizophora mucronata (Hf: Height of the stem; Hh: Height of the crown; Ht = Hf + Hh = Total height of the tree; Lh: Width of the crown; Cb: Circumference of the stem at the base; DBH: Diameter of the tree at 1.30 m from the ground).
3.2. Allometric Relationships
With Avicennia marina, the Log y = A Log [(DBH)2・Ht] + B equation has a correlation coefficient greater than 0.9 for the more woody compartments such as hardwood (R2 = 0.931) and the stem (R2 = 0.908). The use of the variable (DBH)2. Ht is also quite satisfactory (R2 = 0.92) in the case of the total aboveground biomass (Figure 2, Table 4).
This observation is verified in Rhizophora mucronata (Figure 3, Table 5), although the R2 value for the roots is less significant (0.839) under the formula Log y = A Log [(DBH)2・Ht + B]. As for the total aboveground biomass, the coefficient remains the same (R2 = 0.959) as well as with Log y = A Log [(DBH)2・Ht] + B and Log y = A Log DBH + B.
It is the Log y = A Log Cb + B equation that is the most correlated for the estimation of less woody compartments such as the leaves and boughs of A. marina, and this, despite the low value of R2 (respectively 0.847 and 0.826). It is the same for the branches where R2 = 0.876.
Despite the low value of R2 (0.734 to 0.865), it is with the DBH variable that we obtain the best correlation for estimating the weight of branches, leaves and boughs of R. mucronata. With a regression coefficient of 0.93 for both hard woods and total aboveground biomass, the use of basal circumference coefficient Cb is not as conclusive as the use of DBH or [(DBH)2・Ht.
![]()
Figure 2. Allometric relationship on the different aerial compartments of Avicennia marina.
![]()
Figure 3. Allometric relationship on the different aerial compartments of Rhizophora mucronata.
![]()
Table 4. Value of parameters A and B in the relation Log y = A Log x + B according to dendrometric variables x of the Avicennia marina species.
LEGEND: y = phytomass of dry matter in kg; DBH in cm; Ht in m; Cb in cm; R2: regression coefficient of the equation Log y = A Log x + B, i.e. y = kxA such that B = Log k; n = number of trees felled during sampling.
![]()
![]()
Table 5. Value of parameters A and B in the relation Log y = A Log x + B according to dendrometric variables x of the Rhizophora mucronata species.
LEGEND: y = phytomass of dry matter in kg; DBH in cm; Ht in m; Cb in cm; R2: regression coefficient of the equation Log y = A Log x + B, i.e. y = kxA such that B = Log k; n = number of trees felled during sampling.
4. Discussions
4.1. The Equations
The types of Equations (1) and (2) have been used by many authors to estimate aboveground biomass in Kenya [20] [21] [31] , in French Guiana [23] , in South Florida [32] and in Malaysia [25] , where DBH is the main variable. [20] uses the tree circumference to model the aboveground biomass of Ceriops tagal and Rhizophora mucronata. Others such as [24] [33] [34] use (DBH)2∙Ht to estimate it.
The present study tries to value the gains of the equations developed by these various authors by adapting them with the variables of the different compartments of a Mangoky Delta tree (Table 6). It tries to check for any discrepancies between the values of the allometric parameters established elsewhere in the world and those obtained on a smaller scale as the delta.
4.2. Productivity
With 60 t・ha−1 of total aboveground biomass, (all species combined, average tree height = 5.83 m, mean DBH = 8 cm), the Mangoky Delta Mangrove is comparable to that of West Africa where [35] [36] found 55 to 60 t・ha−1 at Saloum, for trees of 5.65 m high. It should be noted that in Puerto Rico, Mangrove yields 58 t・ha−1 year−1 of raw primary products and 9 t・ha−1 year−1 of net primary products [37] .
As part of this study, where tree total heights were 8.3 m and 9.2 m, respectively for Rhizophora mucronata (DBH = 15 cm) and Avicennia marina (DBH = 14 cm), the respective total biomass values of 110 t・ha−1 and 171 t・ha−1 are important compared to the figures found by [38] in Puerto Rico where Ht = 8 m and y = 62.9 t・ha−1 for R. mucronata. However, they are comparable to those measured in Australia where [39] found y = 99.7 t・ha−1 for trees of A. marina of 8.5 m high; and where [40] obtained y = 104.1 t・ha−1 for strata of 7 m. In the USA, [41] found y = 136 t・ha−1 for the species Rhizophora spp. of 9 m high. Those differences are surely linked to latitudinal and longitudinal variations of the studied ecosystems [42] . Indeed, [43] found 240 t・ha−1 for the R. mucronata species in Sri Lanka (8˚2'S), compared to 452.02 t・ha−1 in Kenya (4˚25'S) according to [21] .
The data on the share of the different compartments in the biomass constitution are comparable to the figures obtained by [20] in Kenya, namely for the stems and roots of R. mucronata (Table 7). However, it seems that the Gazi trees have more leaves than the delta ones where about one-third of the total aboveground biomass is provided by the branches.
4.3. Allometric Relationships on the Total Aboveground Biomass
For Rhizophora, the expression of total aboveground biomass can be written in two forms:
Log y = 2.371 Log DBH − 0.606;
Log y = 0.913 Log [(DBH)2・Ht] − 0.851.
In either equation, the regression coefficient remains the same (R2 = 0.959). The values of A and B presented in this study are substantially similar to those found by [24] in Southern Japan and [44] in Indo-Pacific. It is the same for the case of Avicennia where in French Guiana, [23] found A = 2.4 and B = −0.8539 respectively, compared to 0.399 and −0.873 in the Mangoky Delta. In addition to the longitudinal and latitudinal factors reported by [42] , these slight differences seem related to the productivity of the ecosystems studied as we have mentioned above. The physiognomic difference between the species R. apiculata and R. mucronata on one hand and between A. germinans and A. marina, on the other hand also influences the weight of the trees studied.
4.4. Allometric Relationships on Hard Wood
Regarding hardwood (=stem + branches), the most significant allometric relationships established in this study are:
Log y = 0.921 Log [(DBH)2・Ht] − 1.060 for R. mucronata where R2 = 0.973;
Log y = 0.967 Log [(DBH)2・Ht] − 1.284 for A. marina where R2 = 0.931.
Using the variable DBH, the relationship becomes less significant (R2 = 0.962 for R. mucronata and 0.924 for A. marina); the differences in value between [21] parameters A and B and those of this study are respectively 0.14 and −1.9 for R. mucronata. Indeed, the trees studied in Kenya include much more stem (50.2% ± 7.3% of the total biomass) than those evaluated in the Mangoky Delta (40% ± 12.4% of the total biomass) (Table 7).
Regarding the Avicennia marina species, the equation Log y = 2.47 Log DBH − 1.018 obtained in the Mangoky Delta is relatively similar to that established by [26] in Queensland for R. apiculata and R. stylosa. Indeed, the values of A and B respectively are around 2.5 and −1 (Table 6).
4.5. Allometric Relationships on Leaves
The most significant allometric relationships found in the Mangoky Delta are:
Log y = 1.831 Log DBH − 1.319 for R. marina where R2 = 0.746;
Log y = 1.838 Log Cb − 2.699 for A. marina where R2 = 0.847.
The regression coefficient on R. marina obtained in the delta has a mean value compared to that found by [25] at Perak in Malaysia and [21] in Kenya. Be as it may, the results of the different authors show that with the equation of the type Log y = A Log x + B, the R2 values remain insignificant for the Rizophora and Avicennia leaves. Constituting 2% to 10% of the total biomass, leaf weight is insignificant and variable (Table 7).
4.6. Allometric Relationships on Branches
The most significant allometric relationships found in the Mangoky Delta are:
Log y = 2.334 Log DBH − 1.174 for R. marina where R2 = 0.865;
Log y = 2.441 Log DBH − 1.276 for A. marina where R2 = 0.876.
The equation of [21] differs from that established in the Mangoky Delta due to the physiognomy of the trees studied: 26% ± 9.6% of the aerial weight of R. mucronata of the Delta are made up of branches, compared to 9.7% ± 4.8% only for Gazi in Kenya.
4.7. Allometric Relationships on R. mucronata Roots
It is with the variable (DBH)2・Ht, more precisely with the allometric relationship Log y = 1.076 Log [(DBH)2・Ht] − 2.046 (where R2 = 0.839) that the best correlation was found for the roots of R. mucronata of the study area.
5. Conclusion
Based on a destructive method experimented directly in situ, this study has an interest that lies in the availability of the first tools for estimating the aboveground biomass of R. mucronata and A. marina, two main Mangrove species of the Indo-Pacific Region and East Africa, including the Mangoky Delta. The first more targeted equations adapted to sub-regional contexts are now available to
![]()
Table 7. Constitution as % of the aboveground biomass.
complement those already established at larger scales. However, given the lack of baseline data on the productivity of Malagasy Mangroves on the one hand, and because of the small values of the regression coefficients obtained on certain allometric relationships, precautions should be taken in case of extrapolation. It is therefore essential to multiply allometric studies and those on the productivity of Malagasy and East African Mangroves. In any case, the results of this paper can already serve as the first modeling tools for the two main and most widespread species in Madagascar, East Africa and the Indian Ocean.