1. Introduction
Traditional security return models ( [1] [2] [3] ) define the return on a security as the addition of premium for the security’s sensitivity to market fluctuations to the riskless rate. [4] added a size factor in response to findings of higher returns by small firms over large firms to account for the higher default risk and financial distress of small firms [5] . The size effect has been observed empirically for both the U.S. and Asian markets from 1951-1986 and 1982-1988, suggesting that size effects are robust to geographic location and time ( [6] [7] [8] ). Subsequently, [4] added a factor to account for the market overreaction to overpricing well-known, “glamour” stocks and underpricing unknown “value” stocks to support [9] and [5] ’s finding that book-to-market equity explained security returns beyond size and market risk.
These components of return are based on market-based measures from the observations of external sources, such as industry analysts, rating agencies, and regulators. If information asymmetry prevails, managers who operate a firm have more information than outsiders, so that a measure derived from financial statements that reflect the ability of management to make sound financial decisions may increase security returns beyond that indicated by market measures. Such managerial decisions may take the form of capitalizing upon growth opportunities, finding cheap sources of capital, investing in research and development, and making acquisitions in product innovators. In keeping with [10] , who theorized that in an environment in which information is a free good, firm value is more accurately assessed by evaluating the firm’s ability to invest in profit-making opportunities, rather than interpreting market signals. Given that the Internet has made the dissemination of information universal, information may be a free good in frictionless markets. It follows that it is more important to value a firm based on its ability to generate a stream of future cash flows by making judicious investments, rather than interpreting market signals.
Managerial capabilities for investment in profitable projects may be captured by earnings yield = net income/price. Earnings yield is that component of price that may be attributable to profit as reported in financial statements. It reflects profits emanating from business operations of increasing sales, reducing costs, and reinvesting earnings in profitable projects. Earnings yield may influence security returns beyond size and book-to-market equity suggesting that it may be an omitted variable in explaining security returns. This effect may be seen in [11] and [12] who observed that high earnings yield portfolios had higher returns than low earnings yield portfolios. [13] found that earnings yields’ significant influence on stock returns was robust over the entire year. [14] observed higher stock returns for high earnings yield portfolios compared to low earnings yield portfolios.
Earnings yield’s effects on security returns may be based on its ability to predict future cash flows. [15] found that the ability to forecast the next period’s cash flows and to capitalize upon unfavorable news contained in cash flows in a timely fashion, predicted earnings. It follows that earnings are informative in providing expectations of future cash flows that contain such news. [16] extended this result to time periods up to five years, finding that earnings yield significantly predicted future cash flows in both the 1-year and 5-year time periods for US, British, French, and German data. As earnings yield predicts future cash flows, it acts as a measure of residual income. [17] defined residual income as the present value of future discounted cash flows beyond cash flows contained in book value. Residual income is the wealth created by cash flows higher than the cost of raising funds in successive periods. As earnings yield is income earned from successful managerial decisions, income earned in one period leads to that earned in the next period, and so on. There is continuous growth in value from earnings yield, as occurs with residual income. [17] and [18] observed that residual income explained 70% of long-term cross-sectional security returns beyond size, market risk, and book-to-market equity.
We propose that earnings yield will enhance security returns if added to the Fama-French security return model. The rest of the paper is organized as follows. Part 2 provides a theoretical framework. In Part 3, earnings yield is related to security returns. Part 4 provides conclusions and recommendations for future research.
2. Earnings Yield as a Multifaceted Construct
2.1. Earnings Yield and Return on Assets
Return on Assets = Net Income/Total Assets, or the profit generated from the firm’s investment in assets. An increase in earnings yield is expected to increase profits faster than price or investment in assets, suggesting growth in profitability from investment in assets. The variation in return on assets with earnings yield may be represented as a linear or nonlinear function, PQ, with slope of positive change in return on assets to change in earnings yield (see Figure 1).
For a linear function,
(1)
or
(2)
for a quadratic function, where ROAt = return on assets, in period, t, ΔROAt = change in return on assets, in period, t, EPt = earnings yield, in period t, k = constant.
The impact of earnings yield on return on assets may be represented as a Taylor series expansion of a function in return on assets. The Taylor series is the most appropriate formulation in that it assumes infinite differentiability at a point, instead of an interval. The growth in profits over assets may only be sustained over a small, point-type interval, as profit increases will not be sufficient to sustain asset growth over an infinite interval. For a real number that represents the change in return on assets for a particular level of earnings yield at a point, b, a = EPb.
The general Taylor series expansion for f(x) at point a is [19] :
(3)
Substituting,
(4)
![]()
Figure 1. First derivative of return on assets, return on equity, economic value added or equity multiplier to earnings yield. Capital constraint OM,
.
The general Taylor series expansion yields,
The second term in Equation (4) is the first derivative of the ratio of change in return on assets to earnings yield (ΔROAt/ΔEPt). As earnings yield, by definition, indicates that net income increases at a greater rate than stock price, and since return on assets = net income/total assets, we may infer that net income increases more rapidly than total assets due to an increase in earnings yield. In Figure 1, which is the first derivative of return on assets and other outcome variables on earnings yield, the change in net income from earnings yield is represented by movement along the upward-sloping curve PQ. Maximum operational efficiency is attained at point M, with highest return on assets due to change in earnings yield within the firm’s limit on capital, as defined by Ct. For newer firms, the capital constraint is a binding constraint, or Ct, the total amount of capital available is fixed and cannot be increased, whereas an established firm may qualify for additional funding through debt. The slope of the capital constraint, b, then becomes a shadow price of the change in return on assets from an increase in capital beyond Ct, for a certain level of earnings yield. In other words, b is the amount of change in return on assets from a unit change in capital Ct. This conjecture may be expressed as a linear programming model, maximizing return on assets in all of the firm’s divisions based on the premise that Ct may be increased.
Max
(5)
Subject to
(6)
(7)
(8)
or, as a Lagrangian function with a single constraint, Max
(9)
where, x1t, x2t, x3t, x4t are divisions or projects > the cost of capital in time period, t, λ1t, λ2t , λ3t, λ4t, λ5t = Lagrange multiplier; It = industry.
Capital needs vary by industry. For capital-intensive industries, such as energy, capital constraints, although high, may not be binding in that the substantial cash reserves may act as collateral for additional funding of assets, permitting expansion beyond the original capital available. Research-intensive industries, such as biotechnology and pharmaceuticals, need continuous funding of research and development expenses and growth through acquisitions. Established firms may have cash reserves with nonbinding constraints, while newer, less financially stable firms will have binding capital constraints.
At the point of tangency of the capital constraint line OM, to the curve, PQ, Equation (1) satisfies the capital constraint, Equation (6). For low market risk firms, any deviation from predicted return on assets is related to deviations or residuals in previous periods. An example from the oil and gas industry would be drilling for oil below ground in new locations. The form of drilling is traditional, i.e. below ground, but there is some deviation from prevailing practice in that new locations are being pursued. Another example from biotechnology would be robotic surgery. The robot performs surgery under the direction of a physician. The surgery is still directed by the physician, so there is low market risk. However, the use of a robot suggests a deviation from current practice. These deviations in one period are related to those in prior periods. This autocorrelation of residuals may be expressed as:
(10)
where, ξt = deviation of the change in return on assets due to change in earnings yield from a predicted path, in period t, ξt−1 = deviation of the change in return on assets due to change in earnings yield from a predicted path, in period, t − 1, ΔROAt/ΔEPt = the change in return on assets due to the change in earnings yield, period t, ΔROAt−1/ΔEPt−1 = the change in return on assets due to the change in earnings yield, period, t - 1.
The third term in Equation (4) is the second derivative of the change in return on assets due to earnings yield. By definition, the second derivative measures the change in rate of change of a quantity. Figure 2 shows that the change in the rate of change of return on assets increases at a decreasing rate. This indicates d2x/dx2 < 0, along the segment, OQ, and again on the segment QS. At maximum points Q and S, d2x/dx2 = 0, or the change in the rate of change in return on assets due to change in earnings yield gradually diminishes to zero at Q, then increases at a decreasing rate along QS, and then diminishes to zero at S. There are no inflection points as the change in return on assets increases throughout segment QS, and then diminishes to zero at S. There are no inflection points as the change in return on assets increases throughout segment OS, the increase merely occurs at a decreasing rate. Any increase in profitability will only increase return on assets, monotonically up to a point after which incremental additions to return on assets occur more gradually. This line of tangency to the curve of a second derivative lies below the graph of the function of functions approaching a maximum and above the graph of the function for functions approaching the minimum ( [20] ). This line of tangency may represent capital constraints. Capital constraints lie substantially below the change in return on assets from earnings yield for the cash-rich companies, UV. Capital constraints lie just below the change in return on assets from earnings yield for the established firms such as below-ground oil and 5gas companies which generate cash for regular operations (see line MS). Capital constraints lie at the change in return on assets from earnings yield for small firms which are typically capital-constrained (see Figure 1).
Firm-specific risk is measured by the deviation of the change in return on assets due to earnings yield from the predicted path. This risk has no relation to previous risk for startup firms undertaking “moonshot” projects. For example,
![]()
Figure 2. Second derivative of return on assets, return on equity, economic value added or equity multiplier to earnings yield.
startup firms in biotechnology may pursue the development of drugs to treat rare diseases or small drillers in the oil and gas industry may pioneer shale rock extraction of oil. We represent the variability in change in return on assets from changes in earnings yield for periods t through t + n, as error terms. The variance may not vary systematically in the form of a secant line FG (see Figure 3). The point of tangency of FG with the curve PR depicts the rate of change of return assets with earnings yield at two locations, L and N. At these points, the capital constraints are equal to the change in return on assets to the change in earnings yield.
The secant line for heteroscedastic residuals is the line of aberrancy ( [21] ), defined as
(11)
(12)
s = arc length of the secant line, ρ = radius of curvature of the line of aberrancy, at the point of tangency, xt = earnings yield, yt = return on assets.
At this point, we have unsystematic risk = 0, while the highest level of systematic risk occurs at the vertex of the secant line.
2.2. Earnings Yield and Return on Equity
Return on equity is return to the shareholders. Shareholders invest funds in the firm through the purchase of stock, and are rewarded with dividends from net profits and stock price appreciation. Growth in earnings yield suggests that income is growing faster than price or that the firm is increasing its profits on capital invested by shareholders by employing such capital productively in the creation of high-yielding products and services. The variation in return on equity with earnings yield may be represented as a linear or nonlinear function with
![]()
Figure 3. Third derivative of return on assets, return on equity, economic value added, or equity multiplier to earnings yield.
slope of positive change in return on equity to earnings yield.
For a linear function,
(13)
or
(14)
for a logarithmic function, (a), where ROEt = return on equity, in period, t, ΔROEt = change in return on equity, in period, t, EPt = earnings yield, in period t, k = constant.
The impact of earnings yield on return on equity be represented as a Taylor series expansion of a function in return on equity that is infinitely differentiable. The increasing return to shareholders can be achieved in a multitude of ways within a single interval, such as increased dividends, reinvestment of profits from existing products, or innovations in high-yielding new products. This differentiability is at a real number that represents the change in return on equity for a particular level of earnings yield at a point, b. a = EPb.
The general Taylor series expansion for f(x) at point a is [19] :
(15)
Substituting,
(16)
The general Taylor series expansion yields,
The second term in Equation (16) is the first derivative of the ratio of change in the return on equity to earnings yield (ΔROEt/EPbt). As earnings yield, by definition, indicates that net income increases at a greater rate than stock price, and since return on equity = net income/stockholder’s equity, we may infer that net income increases more rapidly than stockholder’s equity along the upward-sloping curve PQ (see Figure 1).
As we make the assumption of investor rationality, we maintain that shareholders would only invest in firms that are capable of achieving a positive return on invested capital. The firm’s ability to produce a stream of profitable products is contingent upon its ability to attract and retain the human capital that either produces product innovations internally or acquires firms that produce such products. Thus, human capital may take the form of technical talent to produce products internally or managerial talent to select acquisitions with profit potential. Maximum operational efficiency is attained at point M, with highest return on equity due to change in earnings yield within the firm’s limit on human capital, as defined by Ht. For certain firms, the human capital constraint is a binding constraint, or Ht, is fixed and cannot be increased, whereas other firms may offer an environment that is more conducive to the talents of human capital engaged in the production of high-yielding products. Therefore, an innovative, creative, entrepreneurial environment may be able to recruit employees beyond the limit imposed by Ht. The slope of the human capital constraint, b, becomes a shadow price of the change in return on equity from an increase in human capital beyond Ht for a certain level of earnings yield. Technology services such as Microsoft Office and the Google Search Engine are examples of high-margin services produced by additional investment in human capital. Additionally, [22] found that managers support the granting of a fixed dividend with gradual growth. [23] observed that institutional investors support the repurchase of shares to boost earnings per share. These results suggest 1) an additional constraint to maintain a threshold level of dividends, with constant dividend growth, and 2) another constraint to achieve a level of earnings per share beyond analysts’ quarterly estimate to elevate share prices.
Max
(17)
Subject to
(18)
(19)
(20)
(21)
or, as a Lagrangian function, Max
(22)
where, x1t, x2t, x3t, x4t are divisions or projects with returns > the cost of capital; λit, λ2t, λ3t = Lagrange multiplier; Dt = the firm’s dividend in time period, t; ks = required return on equity; g = constant growth rate of dividends as defined by the Constant Dividend.
Growth Model:
EPSt = the firm’s earnings per share in time period, t; EPSet = the analysts’ consensus estimate of earnings per share in time period, t.
Human capital needs depend upon the internal capabilities of the firm. If the firm has the scientific talent to develop new products and services internally, human capital needs will remain within the limit, Ht. Examples would include low-technology products like band-aids, over-the-counter medications, and canes and crutches. If the products are highly research-intensive, such as self-driving cars or drones, external scientific or managerial talent will need to be acquired either by recruitment or the acquisition of firms producing the new technology, expanding human capital needs beyond the original level of human capital available.
At the point of tangency of the human capital constraint line to the curve, Equation (13) satisfies the human capital constraint, Equation (18). For low market-risk firms, any deviation from predicted return on equity is related to deviations or residuals in previous periods. An example would be the growth of the demographic of senior citizens, increasing demand for mobility devices. Expansion into new markets such as nursing homes, hospitals, clinics, and retirement homes represents some deviation from prevailing practice. However, the product remains unchanged. These deviations in one period are related to those in prior periods. This autocorrelation of residuals may be expressed as,
(23)
The third term in Equation (16) is the second derivative of the change in return on equity due to earnings yield, or the change of return of equity from the change in earnings yield. Figure 2 shows that the change in the rate of change of return on equity increases at a decreasing rate. The line of tangency to the curve of a second derivative along the segment, OQ, and then OS, may represent human capital constraints. Human capital constraints lie substantially below the change in return on equity from earnings yield for the human capital-endowed companies, UV. Human capital constraints lie just below the change in return on equity from the change in earnings yield for firms which have sufficient human capital resources (see line MS). Human capital constraints lie at the change in return on equity from earnings yield for firms which are typically human capital-constrained (see Figure 1).
Self-driving cars are based on algorithms that permit the vehicle to steer itself and to sense humans or animals in the road and brake instantly. Such algorithms require novel, unprecedented technology. Drone taxi technology would be another case of unique technology. The variance may not vary systematically in the form of a secant line FG (see Figure 3). The point of tangency of FG with the curve PR depicts the rate of change of return on equity with earnings yield at two locations, L and N. At these points, the capital constraints are equal to the change in return on equity to the change in earnings yield.
The secant line for heteroscedastic residuals is the line of aberrancy ( [21] ), defined in Equation (11) and Equation (12). At this point, we have unsystematic risk = 0, while the highest level of systematic risk occurs at the vertex of the secant line.
2.3. Earnings Yield and Economic Value Added
Economic value added (EVA) is a measure of value creation; by definition, EVA = Net operating profit after taxes ? weighted average cost of capital x (total assets ? current liability) [24] . The firm employs its comparative advantage in branding, strategic alliance, and patents and trademarks to create products that achieve sustained profitability over the cost of raising funds from creditors and shareholders. An example would be that of pharmaceutical companies that earn patents that grant exclusive market access for 17 years. This assures a stream of profits that meets the returns demanded by lenders and shareholders and assures residual income into the future. Upon expiration of patents, new products, with their own life cycles assure continuation of net income. Another example would be a hospital which has access to a market of affluent patients. This facility does not have specialized services. They form a strategic alliance with a renowned specialized treatment facility that assures access to these treatments for their patients. The value created by this strategic alliance increases the number of patients to the point where the cost of capital is surpassed.
For a linear function,
(24)
or
(25)
for a quadratic function, where, EVAt = economic value added, in period, t; ΔEVAt = change in economic value added, in period, t; EPt = earnings yield, in period t; k = constant.
The impact of earnings yield on economic value added may be represented as a Taylor EVAt.
Series expansion of a function in economic value added that is infinitely differentiable at a real number that represents the change in equity multiplier for a particular level EVAt of earnings yield at a point, b. a = EPb. The choice of a Taylor series is appropriate, as economic value added may change with the acceleration of net income over price in EVAt myriad ways such as an increase in profit-making projects, decrease in the cost of debt, or decrease in the cost of equity. These variations may only be measured over small intervals, thereby justifying the choice of a Taylor series.
Substituting for
in a Taylor series expansion,
(26)
(27)
The second term in Equation (28) is the first derivative of the ratio of the change in economic value added (ΔEVAt/ΔEPt). As an increase in earnings yield indicates that net income increases at a greater rate than stock price, and since economic value added is the excess of net operating profit over cost of capital, we may infer that operating profit increases more rapidly than cost of capital along the upward-sloping curve PQ (see Figure 1).
Max
(28)
Subject to
(29)
(30)
where, NOPATt = Net operating profit after taxes in time period t, WACCt = Weighted average cost of capital in time period, t, TAt = Total assets, CLt = Current liability; EA = Earning assets.
To maximize economic value added, it is necessary to minimize the weighted average cost of capital, as in Equation (28). The firm’s financial managers must be capable of seeking out the cheapest loans and structuring return payments to private equity investors in such a manner as to minimize the firm’s cost of raising funds. To capitalize upon competitive strengths, the firm’s operating income must always be greater than the cost of capital as this creates high value-added products and services (Equation (30)) and invests in continuous internal research and development or external acquisitions to acquire facilities, scientific talent, and managerial talent. Such resources comprise the firm’s earning assets (Equation (30)) which continue to generate growing profits into the future.
At the point of tangency of the NOPATt/WACCt positivity constraint to the curve, PQ, Equation (26) satisfies the NOPATt/WACCt positivity constraint, Equation (30). For low market risk firms, any deviation predicted deviations in one period are related to those in prior periods. An example would be the sudden decline in net income, and in turn, earnings yield from the drop in oil prices to traditional in-ground oil extractors. As net operating income falls, large extractors diversify their operations to refining crude oil and producing oil by-products such as paper and fertilizer. Their operating income reductions are similar to those of previous periods of cyclical oil price reductions. This autocorrelation of residuals may be expressed as,
(31)
Figure 2 shows that the change in the rate of change of economic value added increases at a decreasing rate. This indicates that d2/dx2 < 0 along the segment, OQ, and again on the segment, QS. At maximum points Q and S, The line of tangency to the curve of a second derivative lies below the graph of the function for functions approaching a maximum and above the graph of the function for functions approaching the minimum ( [20] ). This line of tangency may represent NOPATt/WACCt constraints. NOPATt/WACCt lie substantially below the change in economic value added from earnings yield for the companies that achieve substantial value creation, UV. Equation (30) constraints lie at the change in economic value added from earnings yield for firms who are challenged in maintaining NOPATt > WACCt (see Figure 1).
Shale rock oil drillers experience a substantial erosion of operating profits with the erosion in oil prices, if they have not diversified into unrelated industries. We represent the volatility in operating profits for periods t through t + n, as error terms, with μ as the mean of the distribution of error terms. Adapting [21] , this condition is captured by the third derivative in the Taylor series (see Figure 3), which has a path of error terms represented by a path of aberrancy in the form of a secant line, FG. The point of tangency of FG with the curve, PR depicts the rate of change of economic value added with the change in earnings yield at two locations L and N. At these points, Equation (30) constraints are equal to the change in economic value added to the change in earnings yield.
The secant line for capital constraints is the line of aberrancy ( [21] ), defined as,
(32)
(33)
s = arc length of the secant line; ρ = radius of curvature of the line of aberrancy; At the point of tangency; xt = earnings yield; yt = economic value added, EPt; At this point, we have unsystematic risk = 0, while the highest level of systematic risk occurs at the vertex of the secant line.
2.4. Earnings Yield and Equity Multiplier
The equity multiplier = Total Assets/Stockholder’s Equity. This is a measure of the proportion of a firm’s assets that are financed by debt. If earnings yield increases, the increase in net income may be due to a signal from a rising equity multiplier that the firm has the ability to fund asset purchases through debt. As an example, established brick-and-mortar retailers have substantial unused retail space transmitting the signal that the retailer has the collateral to purchase inventory. If sales, and in turn, net income increases more rapidly than price (rising earnings yield), the profit from retailing is sufficient to meet debt payments. Rising earnings yield supports rising debt capacity as measured by the equity multiplier.
For a linear function,
(34)
or,
(35)
for a hyperbolic function, where EMt = equity multiplier in period, t; ΔEMt = change in equity multiplier, in period, t; k = constant.
The impact of earnings yield on the equity multiplier may be represented as a Taylor series expansion of a function in equity multiplier that is uniquely differentiable as a real number that represents the change in equity multiplier for a particular level level of earnings yield at a point, b. a = EPb. The change in debt capacity is infinitely differentiable at a point with assets such as real estate providing high debt capacity as as collateral, and equipment or securities providing modest collateral, and small business income providing minimal security for debt.
Substituting for f(a) in a Taylor series expansion,
(36)
(37)
The second term in Equation (37) is the first derivative of the ratio of the change in the equity multiplier to the change in earnings yield (ΔEM/ΔEPt). As earnings yield, by definition, indicates that net income increases at a greater rate than stock price, and since the equity multiplier signals the firm’s capacity to raise funds through debt, we may infer that the firm’s debt capacity grows with rising profits along the upward-sloping curve, PQ (see Figure 1).
Max
(38)
Subject to
(39)
 (40)
(40)
where, REV(tradt) = Revenue from traditional sources in time period, t; REV(online) = Revenue from online sources in time period, t; REV(nontradt) = Revenue from nontraditional sources in time period, t.
To maximize EMt/EPt, the firm will need to expand the funds available through debt by demonstrating that it has the profit and cash flow to meet interest payments. It may accomplish this objective by continuously increasing revenue (Equation (39) and Equation (40)). Traditional sources of revenue (such as in-store sales may be insufficient, so that online sales may be supplemented with growth in the online division. Leasing extra space to convenience stores and package delivery, or creating amusement arcades are nontraditional uses of retail space to generate additional revenue.
At the point of tangency of the positivity constraint to the curve, PQ. Equation (35) satisfies the positivity constraint. For low market risk firms, any deviation from predicted deviations in one period are related to those in prior periods. This autocorrelation of residuals may be expressed as in Equation (31) adapted to the equity multiplier, Figure 2 shows that the change in the rate of change of economic value added increases at a decreasing rate. This indicates that the second derivative < 0, along the segment, OQ, and again on the segment, QS. At maximum points, Q and S, the second derivative = 0, or the change in the rate of change in economic value added due to earnings yield gradually diminishes to zero at Q, then increases at a decreasing rate along QS, and then and then diminishes to zero at S. The line of tangency may represent Equation (39). The change in equity multiplier increases from earnings yield for the companies that achieve substantial increases in debt funding of assets, UV. Such constraints lie just below the increase in debt capacity from earnings yield for the firms which have modest increases in debt funding (see line MS), These constraints lie at the change in equity multiplier from earnings yield for firms who are challenged in maintaining revenues to be sufficient to fund interest payments on additional debt (see Figure 1).
Gas stations with convenience stores may be franchises or independently owned independently-owned stores do not have the debt capacity of national franchises. They may only increase debt capacity through cobranding, carrying unique merchandise, or providing special services such as car washes. Their revenue from all sources may be highly variable depending upon the effectiveness of their marketing campaigns. If we represent the variability in revenue for periods t through t + n, as error terms with mean, μ. Adapting [21] , this condition is captured by the third derivative in the Taylor series (see Figure 3), which has a path of error terms represented by a path of aberrancy in the form of a secant line FG. The point of tangency of FG with the curve, PR depicts the rate of change of the equity multiplier with earnings yield at two locations, L and N. At these points, Equation (39) constraints are equal to the change in equity multiplier to the earnings yield, or earnings yield is measurable at these locations.
The secant line for capital constraints is the line of aberrancy ( [21] ), defined as in Equation (33) and Equation (34). At this point, we have unsystematic risk = 0, while the highest level of systematic risk occurs at the vertex of the secant line.
The Taylor series of the change in earnings yield to return on assets, return on equity, economic value added and equity multiplier is a 4th order Taylor series expansion [25]

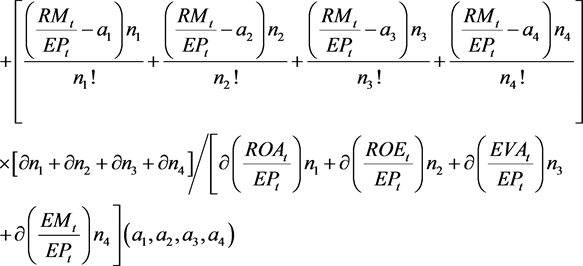 (41)
(41)
3. Earnings Yield and Security Returns
Earnings yield consists of net income = revenue ? expense, which involves the receipt and payment of cash. This cash management is reflective of managerial decisions that include information about business cycles (periods of strong and weak cash inflows and outflows) and incorporate positive and negative news when they occur, and not when they appear (possibly months later), in the end-of-year financial statements. As positive cash flows accumulate over a 1 - 5 year period, firm value creation occurs, increasing security returns. Earnings yield is informative in describing future cash flow, which in turn, explain security returns.
A second-order Taylor series expansion may be created. The expansion has xt = EPt, earnings yield, yt = RETt, about the point (a, b),
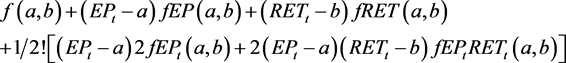 (42)
(42)
The entire COMPUSTAT database was selected with incomplete data being filtered out to yield a sample of 55,457 observations of net income, security returns, size, and book-to-market variables from 2008-2018 (March, 2018). The
![]()
Table 1. Results of regressions of security returns on the risk free rate, volatility, earnings yield, size, and book-to-market equity.
*p < 0.05, **p < 0.01, ***p < 0.001.
COMPUSTAT database from Standard and Poor’s provides financial statements, security prices, dividends and earnings for publicly traded companies in the United States. As shown in Table 1, earnings yield significantly predicted security returns beyond size and book to market equity consistently in each year of the study period, with coefficients of 0.22 - 7.99, p < 0.05. While size and book-to-market equity showed significance in explaining returns in certain years, it was only earnings yield of the predictors (including volatility and risk-free rate) that was significant in every year.
The proposed modified security return model is,
 (46)
(46)
Rj = return on security j, Rf = risk-free rate, Rm - Rf = market risk premium, SMB = firm size variable, HML = firm book-to-market variable, EYIELD = earnings yield variable.
4. Conclusions and Recommendations for Future Research
This paper has added earnings yield as a measure of product attributes and the quality of managerial decision-making to explain security returns beyond risk measures and investment aberrations such as size variations, and book-to-market variations. This approach views security returns as more than a manifestation of market behavior as observed by distant outsiders, such as financial advisors and investment analysts. It views returns in terms of financial fundamentals, i.e. as the direct consequence of the ability of the firm to generate income that grows more rapidly than price through investments in assets, projects that earn more than the cost of capital and by increasing debt capacity.
As cash flow is an outcome of earnings yield, i.e. the regression of cash flow on earnings yield is highly significant (coefficient = 8.76 × 10−2***, p < 0.001), even though cash flow has no significant impact on security returns, future research should identify additional mediating variables that cash flow would influence, which, in turn, would affect security return. As high profit margin overcomes rising costs of production, future research should assess the impact of including profit margin as an additional explanatory factor in the security return model.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.