Simulink/MATLAB Model for Assessing the Use of a Centrifugal Pump as a Hydraulic Turbine ()
1. Introduction
Given the right hydrologic circumstances, a viable source of renewable energy can be found in hydropower. Hydropower is attained through the transfer of potential and kinetic energies stored in liquid into mechanical energy. This transfer is traditionally facilitated by a specific type of turbomachinery called a hydraulic turbine. However, this does not necessarily always have to be the case. For a microhydropower installation, there may be the option for this energy transfer to be performed by a centrifugal pump instead.
The reasoning for a centrifugal pump to be used instead of a hydraulic turbine in producing power for a microhydropower system is multifaceted. Centrifugal pumps are far more ubiquitous than turbines in the turbomachinery market, therefore being more readily available to the consumer. Additionally, they are cheaper. Hydraulic turbines undergo rigorous CFD simulation design and testing to establish their blade geometries and ranges of operation. This results in a refined but very expensive final product. Centrifugal pumps are thus presented as a logical alternative seeing that they can physically perform the same task as a hydraulic turbine albeit at a reduced efficiency [1] .
Knowing this, it is worth investigating the viability of using a centrifugal pump in a microhydropower application for cost reduction. Is such a cost reduction warranted in the context of reduced efficiency?
The Simulink/MATLAB simulation described within this work strives to aid in answering such a question. It uses the concept of flow geometry to describe the behavior of the three characteristic turbomachinery parameters (head, power, efficiency) for two common types of centrifugal pump geometries (radial and backswept).
2. Simulink Model
The Simulink model is meant to allow for a readily available comparison between pump and turbine modes for a turbomachine whose original purpose is that of a centrifugal pump. It is composed of four subsystems representing different impeller operating modes and impeller geometries, as shown in Figure 1.
They include a backswept pump, backswept PAT, radial pump and radial PAT. Backswept impellers on a centrifugal pump have blades that sweep counterclockwise as they protrude from the center of the impeller. Conversely, radial impellers have blades that remain straight as they protrude outwards from the inner diameter to the outer diameter. All four employ the same constant values for gravity, density, inner diameter, outer diameter, and rotations per minute (RPM).
Figure 2 offers a more in-depth look into the radial pump subsystem. This subsystem, as do the rest, reads from left to right. This means that it receives inputs on the left-hand side, called sources in Simulink, and then has outputs, also called sinks, finishing on the right.
Figure 3 displays the inner workings of the Backswept Pump subsystem. The blocks are different colors and this serves to bookkeep which values are directly based on the absolute inlet velocity iteration. Constants or assumptions that require no computation and are assigned from the start of the simulation are in a dark green colorway. Some values will always be constant due to the geometry of backswept and radial blades, and as such, are also included in that color. The light blue blocks indicate that the value requires a computation but does not require an incremented iteration, thereby having a scalar result. They are User-Defined Simulink Functions, a block type which allows for the customized manipulation of scalar inputs. The darker blue blocks represent the parameters directly based the absolute inlet velocity vector and are therefore iterated and are vectors themselves. They lead directly to the head, power and efficiency curves. Their block type is called the MATLAB Function block, which essentially allows
![]()
Figure 1. Simulink model of two turbomachines, one radial and one of backswept geometry, for pump and pump-as-turbine modes.
the user to write a mini-script. Seeing as the Simulink User-Defined Function blocks only allowed for scalar inputs, these MATLAB Function blocks were a must for dealing with the calculations that employed the inlet absolute velocity vector.
The other block types that are used included the Display blocks and the Mux blocks. Figure 4 has both, with display blocks usually coming after a function
block and a mux block coming before. The purpose of the display block as the name implies is to show values in the simulation, without any additional prompting. Mux blocks serve to combine several different input signals to then output them as a vector or a bus output signal. This makes them convenient for use in combination with Simulink user-defined functions, seeing as one can efficiently track multiple scalar inputs inside a one-row vector.
Figure 5 is the radial turbine subsystem. One of the differences between the pump and PAT modes is that there are substantially more dark blue blocks. This means that the PAT calculation is generating more values that use the inlet absolute velocity than the pump calculation. This is mathematically true, seeing as pump torque and pump shaft work is constant due to the model constraints discussed in the Model Limitations sections.
Ultimately, the computations performed within these subsystems solve for multiple unknowns which eventually allow for the calculation of that turbomachine’s head, power output and efficiency over a flow rate domain. The time step is set to zero so that the entirety of the inlet velocity vectors is taken instantly for the calculation. Seeing as the inlet velocity vector is the independent variable that drives the model and not time-dependent, this time step setting is necessary.
3. Flow Model
The flow model utilizes the concept of velocity triangles to solve for circumferential, relative and whirl velocities along with flow rates for both inlet and outlet sections [2] . Velocity triangles describe the velocities of the fluid and turbomachine at various points at both the inlet and the outlet. In total, there are eight triangles programmed into this Simulink model. There are two for backswept pump inlet and outlet, two for backswept PAT inlet and outlet, and the same arrangement for the radial geometry.
Circumferential velocity U as the name implies deals with the velocity at the circumferences of the inner and outer diameters. For backswept and radial centrifugal pumps, the inner and outer circumferential velocities are unequal. Relative velocities
deal with the velocity of the fluid relative to that of the rotating blade. The whirl velocity
or
is the tangential (horizontal) component to absolute velocity. Flow velocity
may also be present but is not necessary in the calculations done by this simulation. Absolute velocity V is fluid velocity that is relative to absolute space. The model calls for the use of two absolute inlet velocity vectors with one being used for the pump and one being used for a turbine. This is because the turbine mode sometimes requires a higher relative inlet velocity in order to achieve the same flowrates as the pump mode.
These four velocities create triangles at the inlets and outlets of the turbomachines as seen in Figures 6-8. The proportions of the triangles are characterized by their angles.
is the angle made by the absolute velocity with the circumferential velocity.
is the blade angle. The setting of
to be less than 90˚ creates a backswept blade geometry while
creates a radial geometry. Geometric relationships become evident among
and
and their turbine counterparts once a single centrifugal turbomachine is used for both pump and PAT operation modes.
While the relationship of
is straightforward, that is not so much the case for
. This angle would be needed to calculate the relative turbine inlet velocity
if one were to use the Law of Sines. Instead, it is possible to employ The Law of Cosines as seen in Equation (1) to try and circumvent the use of
.
![]()
Figure 6. Backswept pump outlet and backswept turbine inlet velocity triangles. The orange lines indicate the absolute velocity, the green lines represent the relative velocity, and the blue stand for the whirl velocity and the black line denotes circumferential velocity.
![]()
Figure 7. Radial velocity triangles for both pump and turbine modes.
![]()
Figure 8. Graph of Equation (1) given angle values used in Table 2.
(1)
However, one can see that the resultant equation will not yield a real answer unless the absolute inlet turbine velocity exceeds the outer diameter circumferential velocity. This is a constraint of this simulation because the rotations per minute is kept constant, therefore making the circumferential velocities constant as well. As such, it is not mathematically possible to compute
nor
, at least before the desired RPM constant is reached. A low absolute inlet velocity cannot physically induce an instantaneous 500 RPM on the turbomachine. It becomes readily evident that in order to calculate
in relation to
, the relative velocity
of the water entering the PAT has to be larger than the PAT’s circumferential velocity
in order for the Turbine Inlet triangle to be possible. Given an RPM of 500, the absolute inlet turbine velocity
would have be larger than 13.1 m/s before the relationship in Equation (1) would yield a real, non zero, result. After this point, the value of
would follow the curve given in Figure 8 assuming that
and knowing that
. Therefore, an appropriate angle is assigned for the sake of simulation which could also be measured if given an actual centrifugal pump.
3.1 Slip Factor
Slip factor is accounted for using the empirical correlations of Stanitz Equation (2) and Wiesner Equation (3).
(2)
(3)
It is defined as a measure of the deviation in angle at which the fluid leaves the impeller from the blade. This is represented as a ratio of the actual outlet whirl velocity divided by the ideal outlet whirl velocity, as seen in Equation (4).
(4)
It accommodates slip loss in the calculation, a phenomenon that results due to a difference in pressure between the leading and following parts of the impeller blade. The addition of slip factor helps to create a noticeable increase in backswept efficiency, seeing as it helps to illustrate the tendency of the fluid to “hug” the following side of the backswept blade during operation. This holds true only for the pump mode however, seeing as the outlet whirl velocity for a turbine is assumed to be zero.
4. Simulation Model
This model is driven by absolute inlet velocities that must be assigned and incremented as a one-dimensional vector inputs. They begin at zero and increment at intervals of 0.1 m/s up to the maximum assigned absolute inlet velocity, with each interval yielding new values for head, power and efficiency at the specified mode.
The No-Slip condition was applied on the inlets for the pump mode and the outlets for the Pump-As-Turbine mode. This resulted in the whirl velocities
in these areas being declared zero. This is due to the structure of the velocity triangle, which in those locations is a right triangle that therefore eliminates the whirl velocity
and the slip phenomenon. System curves were not generated due to a lack of pressure data for the suction and discharge regions. Losses were also declared negligible. The starting angle values for the velocity triangles were assumed as well based on typical centrifugal pump geometries. Only the smallest possible number of angles was declared, and the rest were attempted to be solved for based off the impeller geometries. The typical constants for gravity and water density were used.
4.1. Accompanying MATLAB Code
A MATLAB script was created alongside this Simulink model to help verify the consistency of the results. Constants are first declared consisting of things such as density, area and the turbomachinery angles. Memory is then allocated through the use of the zeros function before the actual calculation portion to increase code speed and robustness. The code uses two For-loops to compute the same final parameters of head, power in and out, and efficiency. Just like the Simulink mode, this is driven by the iteration of the inlet absolute velocity which is indexed with i and set to terminate at a pre-decided and declared maximum inlet absolute velocity. Any value that does not require existing as a vector exists as a scalar quantity, thereby explaining the lack of vectors in the outlet sections of the loops. The equations used in the calculation portion of this script are identical to those used in the Simulink model. Upon termination of the loops, MATLAB’s graphing functions are employed to generate the twelve final plots.
4.2. Discussion of Equations Used
All computations and results are presented in SI units. As such, some conversion factors are present within the model and code equations. This is evident with one of the first computations, the Shut-off head, also known as maximum pump head. It was calculated using Equation (5), which was in customary units thereby requiring the conversion of the outer diameter into feet and then the conversion of the head result back into meters.
(5)
The circumferential velocities of Equation (6) and Equation (7) are computed as a product of the RPM and the respective diameter, with a linearizing conversion factor to address the rotation.
(6)
(7)
Seeing as the model computes using a constant RPM, this thereby makes the circumferential velocity constant as well. As mentioned previously, the other velocities are computed using triangular relationships such as the law of sines, cosines and right triangle rules.
The Pump Head equation used is Equation (8).
(8)
It is a summation of the shut-off head along with the difference between the squared outlet and inlet relative pump velocities. Pump head can be defined as the amount of pressure that a pump can supply to the fluid. It is then used in Equation 6 to compute the power out, the power transferred from the pump to the fluid via mechanical energy.
Similarly, turbine head in Equation (9) is a summation of the difference between the squared inlet and outlet turbine relative velocities plus the static head that the turbine is operating at.
(9)
Shaft torque and subsequent shaft work for the backswept pump is calculated through Equation (10) and Equation (11).
(10)
(11)
The torque equation itself is a form of Euler’s Turbomachinery Equation. It is the difference in the fluid through the turbomachine. For the Pump-As-Turbine mode, the outlet whirl velocity
was assumed to be zero, thereby making the power dependent solely on the inlet velocities as seen in Equation (12) and Equation (13).
(12)
(13)
The turbine efficiency of Equation (14) is instead a ratio for power output, the power produced by the turbine also turbine shaft work, to power input, which is the hydraulic power of the water entering the system.
(14)
5. Discussion of Results
The simulation model was run using the parameters listed in Table 1 and the angles listed in Table 2.
The results are twelve graphs presented in Figures 9-20. Graphs of Figures 9-14 compare parameters between pump and turbine modes for their respective geometries, while the graphs of Figures 15-20 compare parameters between geometries for their respective modes.
Figure 9 is a comparison of the turbine head to the pump head for a backswept impeller geometry.
Under the given conditions, the backswept pump mode is unable to provide any more head to the fluid once flow rate exceeds 2.6 m3/s. This is why the power
![]()
Table 2. Selected angle values. The angles whose value includes another angle indicate a geometric relationship.
![]()
Figure 9. Head curve-backswept impeller.
output for the backswept pump mode terminates at 2.6 m3/s, while the backswept turbine mode power output continually increases with flow rate in Figure 10.
The efficiency curve for the backswept turbomachine shows that the pump is more efficient than the turbine by approximately 12% when taking the maxima of the curve in Figure 11.
The radial impeller geometry head curve of Figure 12 shows the pump head beginning at approximately 17 m and terminating at 0 m when the flow rate reaches approximately 3.5 m3/s.
The power curve for the radial pump mode shown in Figure 13 is much larger than its backswept counterpart in Figure 10.
Regarding their respective power equations, the only term that is different between the two is head. Inlet flow rates for backswept and radial pumps are equivalent. The head produced by the radial pump is much larger initially than the backswept head, as seen in Figure 12. This is because that outlet relative
velocity is much larger for the radial configuration under the given velocity triangle angles. This explains why the radial pump power curve in Figure 13 is larger than its backswept counterpart in Figure 10.
An unexpected but explainable result is shown in Figure 14. The turbine mode is more efficient than the pump mode for the radial configuration by about 25%, but severely limited in it’s operational flow rate. It terminates at about 76% for 1 m3/s. This is due to the geometric variation for the intake of water at the pump inlet and the PAT inlet. Figure 7 shows that the pump inlet
![]()
Figure 15. Backswept and radial impellers in turbine mode.
for a radial impeller has the water coming in at a blade angle 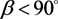 while it’s turbine counterpart has the water entering at
while it’s turbine counterpart has the water entering at![]() . This means that
. This means that![]() , the inlet flow rates are not equal between pump and PAT mode. In fact,
, the inlet flow rates are not equal between pump and PAT mode. In fact, ![]() along the entirety of the absolute inlet velocity vector. This explains why the pump mode is able to produce power over a larger flow rate domain than the turbine. Additionally, the PAT efficiency of Equation (14) is dependent on the inlet flow rate through its denominator
along the entirety of the absolute inlet velocity vector. This explains why the pump mode is able to produce power over a larger flow rate domain than the turbine. Additionally, the PAT efficiency of Equation (14) is dependent on the inlet flow rate through its denominator![]() . The Equation (15) details
. The Equation (15) details ![]() and one can see that
and one can see that ![]() contributes to making it smaller and
contributes to making it smaller and
![]()
Figure 16. Power curves for backswept and radial impellers in turbine mode.
![]()
Figure 17. Efficiency curves for backswept and radial impellers in pump mode.
thereby contributes to an overall smaller denominator for the efficiency calculation of Equation (14) and therefore a higher turbine efficiency.
![]() (15)
(15)
Figure 15 shows the turbine head for the radial and backswept geometries. The radial turbine head, as mentioned previously, starts off about 7 m higher than the backswept turbine head. Its slope however is more aggressive and it terminates earlier as a result.
This trend is expectedly duplicated in the Power Curve graph of Figure 16.
![]()
Figure 18. Head curves for backswept and radial impellers in turbine mode.
![]()
Figure 19. Power curves for backswept and radial impellers in turbine mode.
The backswept efficiency is significantly larger in pump mode than the radial efficiency, by approximately 30% as showcased in Figure 17.
The radial turbine mode provides essentially the same amount of head and thereby the same amount of power as the backswept turbine mode, while doing so more gradually over a longer flow rate domain. This can be seen in Figure 17 and Figure 18.
This trend type holds true for the radial and backswept efficiencies as well, with the two being equal yet radial covering a larger breadth of operation, as
![]()
Figure 20. Efficiency curves for backswept and radial impellers in turbine mode.
shown in Figure 20.
6. Simulation Model Limitations
The fundamental limitation of this simulation model is that there is not yet a way to predict the outlet velocities so that they can change depending on inlet velocity. With the configuration of the model as it is now, the outlet velocities are constants that depend on the circumferential velocity, which in and of themselves are constant due to a constant RPM. To put it in terms of values, it is not physically feasible for an absolute inlet speed of 0.1 m/s to translate into an absolute outlet speed that is dependent on a circumferential velocity calculated using 500 RPM. This insinuates why changes in certain angle values or machine parameters can cause the efficiency to either become negative or larger than one. Ideally, Euler’s Equation for Turbomachinery would be used to find the outlet velocity while incrementing the inlet velocity. This would however require the manufacture to provide head curve data. Using this, the outlet velocity for a given head curve could be computed while varying the inlet velocity. This could then be used as a basis to calculate the remaining velocities.
The fact that the absolute outlet velocity cannot be computed in the model means that the constant circumferential velocity must be relied upon when trying to describe a geometric relationship between the backswept pump outlet and backswept turbine inlet angles. It becomes readily evident that in order to calculate ![]() in relation to
in relation to![]() , the relative velocity
, the relative velocity ![]() of the water entering the PAT has to be larger than the PAT’s circumferential velocity
of the water entering the PAT has to be larger than the PAT’s circumferential velocity ![]() in order for the Turbine Inlet triangle to be possible. Figure 6 illustrates this visually and Equation (1) describes this mathematically via Law of Cosines.
in order for the Turbine Inlet triangle to be possible. Figure 6 illustrates this visually and Equation (1) describes this mathematically via Law of Cosines.
It is also worth noting that the inlet whirl velocity for a radial turbine is not equivalent to the outer diameter circumferential velocity, unlike outlet whirl velocity for the radial pump. This is somewhat surprising seeing as the geometries of the two configurations are identical. It is not surprising though when examined in the context of the constant RPM. The model assigns the turbine inlet a circumferential velocity based on 500 RPM for the entirety of the absolute inlet velocity vector, from 0.1 m/s to it’s maximum. This is not physically feasible.
Turbines typically do operate at constant RPM values, so the fact that the model is set to do so is not abnormal. This is because it is often desirable to maintain a balance between the Prime Mover Torque and the Electromagnetic Drag in the generator. If this is done, then the rotor speed will remain constant. The power generated in the turbine comes from the prime mover shearing it’s magnets against the magnetic field of the stator windings, thereby generating electromagnetic drag. The stator windings are copper structures which facilitate the transfer of the kinetic energy to electric energy.
7. Conclusions
Keeping in mind the limitations that this model possesses, it can still be used as a starting point for assessing the viability of the use of a centrifugal pump as a PAT machine. If head curves from a manufacturer can be acquired at a desired constant RPM, especially the equations for these curves, it can be easily adjusted to provide the correct results.
As it stands currently, it can be used to facilitate a simple comparison. It can give the user a potential gauge of the size, geometry and blade number. Additionally, it is necessary to note that the values of Torque and Power Output for the Backswept and Radial Turbines are correct. This is due to the No-Slip condition that assigned for both the pump inlet and the turbine outlet, in which it resulted in the Outlet Turbine Whirl Velocity ![]() being 0.
being 0.
The zero Whirl Velocity is a common assumption for turbines as it idealizes the complete transfer of energy from fluid to kinetic form. With this in mind, one can see that Equation (12) and Equation (14) all change in response to the change in the inlet velocity. The curves that they provide are quite reasonable as well, as seen in Figure 20 above.
Given the head curves at a specified RPM, after some adjustments, the model can be used to create a value index. This index would be a ratio of turbomachine cost to its efficiency. This way, a centrifugal pump operating as a PAT could be then compared to a turbine in terms of dollars per percent of efficiency. The higher the ratio is, potentially the worse the choice will be. A lower ratio would mean that the turbomachine would initially cost less but run more effectively. Such may be expected for a centrifugal pump seeing as they are significantly lower in price than microhydropower turbines.
Acknowledgements
The authors want to thank the Mechanical Engineering Department at the University of Colorado Denver for the support given for this project. Also, the authors want to thank the IT department for access and use of the necessary software to run the different codes for the simulations.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.