1. Introduction and Preliminaries
Special matrix functions appear in connection with statistics [1] , Lie groups theory [2] , mathematical physics, theoretical physics, group representation theory, and orthogonal matrix polynomials are closely related [3] [4] [5] . In [6] [7] [8] , the hypergeometric matrix function has been introduced as a matrix power series, an integral representation and the hypergeometric matrix differential equation. In [9] - [18] , extension to the matrix function framework of the classical families of p-Kummers matrix function and Humbert matrix function have been proposed. The third author has earlier studied the p and q-Horn’s H2,
-Kummer matrix functions of two complex variables under differential operators [19] [20] . The reason of interest for this family of hypergeometric matrix functions is due to their intrinsic mathematical importance. The main purpose of this paper is to study some properties of the Horn matrix function of two complex variables
which is a matrix extension of Horn scalar function [21] [22] [23] [24] .
Throughout this paper, for a matrix A in
, its spectrum
denotes the set of all the eigenvalues of A. If A is a matrix in
, its two-norm denoted by
and defined by
where, for a vector
,
is the Euclidean norm of y.
Let us denote
and
the real numbers [25]
(1)
If
and
are holomorphic functions of the complex variable z which are defined in an open set
of the complex plane and A is a matrix in
such that
, then the properties of the matrix functional calculus [26] , it follows that
(2)
Hence, if B in
is a matrix for which
also and if
, then
(3)
The reciprocal gamma function denoted by
is an entire function of the complex variable z. Then for any matrix A in
, the image of
acting on A denoted by
is a well-defined matrix. Furthermore, if
is an invertible matrix for all integer
(4)
then
is an invertible matrix, its inverse coincides with
and from [6] , one gets the formula
(5)
Jódar and Cortés have proved in [25] , that
(6)
Taking into account the Schur decomposition of any square complex matrix A, by [7] it follows that
and
(7)
The hypergeometric matrix function is defined by the matrix power series in the form
(8)
If n is large enough, then for C in
such that
is an invertible matrix for all integer
, then we will mention to the following relation already established in Jódar and Cortés [7] in the form
(9)
Let us denote
(10)
and
(11)
One of them is the Horn matrix functions of two complex variables (see [27] )
2. Radius Regularity of Horn Matrix Function
The Horn matrix function
of two complex variables will be written in the form
(12)
where
in addition A, A’, B, B’ and C are positive stable matrices and commutative matrices in
such that
is an invertible matrix for all integers
.
For simplicity, we can write the
in the form
,
in the form
,
in the form
,
, and
in the form
.
Now we begin the study of the conditions so that Horn matrix functions
converges for
,
.
By hypothesis
(13)
thus there exists a positive number
such that
(14)
From (7), (14), theorem 1 of [25] and taking into account that
, it follows that
(15)
For positive numbers μ and n, we can write
(16)
Using (6), (17) in (16), we have
by the comparison theorem of numerical series of positive numbers one concludes the absolute convergence of series (12).
By (5), (6) and the lemma 2 of [25] , one gets
(17)
From (12) and (17), we get
(18)
where
where
and C are matrices in the space
of the square complex matrices of the same order N, satisfying the following conditions
(19)
and
and
are positive stable matrices. (20)
This is an integral form of the Horn matrix function.
3. Recurrence Matrix Relations
Some recurrence matrix relations are carried out on the Horn matrix function. In this connection the following contiguous functions relations follows, directly by increasing or decreasing one in original relation
(21)
Similarly
(22)
The same way, we can get some examples of contiguous functions relations directly
(23)
Note that
and
.
4. The Horn Matrix Function under the Differential Operator
Consider the differential operator D as given in [28] , takes the form
(24)
where
and
. The contiguous function relations of the Horn matrix function under the differential operator D will be given as follows
(25)
(26)
and
(27)
From (25), (26) and (27), it follows at once that
(28)
From (26), (27) and (28), we get
(29)
Operating with D on the Horn matrix function of two complex variables yields
(30)
Operate with
on the Horn matrix function, we obtain
(31)
(32)
and
i.e.,
(33)
Similarly, for
, we have
(34)
(35)
and
(36)
i.e.,
(37)
Hence the Horn matrix function
is a solution of the partial differential equations in the forms (33) and (37).
Now, we see that
(38)
From (32), (35) and (38), we have
(39)
The
-operator has been defined of two complex variables by Sayyed [28] in the form
(40)
where
where N is a finite positive integer.
We have by mathematical induction the following general form of differential operator
to Horn matrix function in the form
(41)
5. Hadamard Product of Two Horn’s Matrix Functions
Let
and
are commutative matrices in
such that
are invertible matrices for all integers
,
.
The Hadamard product of two Horn’s matrix functions of two complex variables is defined in the form
(42)
where
Now, we prove that the Hadamard product of two Horn’s matrix functions of two complex variables convergence for all z and w with
and
. If n is large enough, one can write
, then the following relation is satisfied [7]
(43)
Denote
(44)
Note that
(45)
Then by relation (43)-(45) for m large enough, such that
, it follows that
(46)
Thus, the power matrix series (42) is convergent for all complex numbers
and
.
From relation (17) and the conditions (19) and (20), we can write
(47)
where
Therefore, an integral representation for Hadamard product of two Horn’s matrix functions is obtained.
Contiguous Functions Relation for Hadamard Product of Two Horn’s Matrix Functions
For the Hadamard product of two Horn’s matrix functions
, we can define the contiguous function relations as follows
(48)
(49)
(50)
(51)
(52)
(53)
(54)
(55)
(56)
and
(57)
For all integers
and
we deduce that
(58)
(59)
(60)
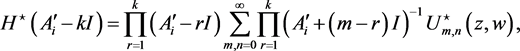 (61)
(61)
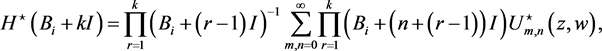 (62)
(62)
 (63)
(63)
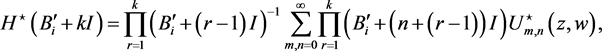 (64)
(64)
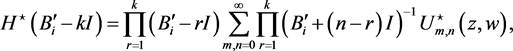 (65)
(65)
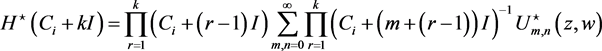 (66)
(66)
and
 (67)
(67)
The Hadamard product of two Horn’s matrix functions is affected by the differential operator D, so, for all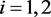 , we obtain that
, we obtain that
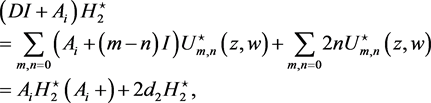 (68)
(68)
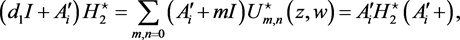 (69)
(69)
 (70)
(70)
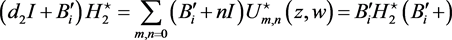 (71)
(71)
and
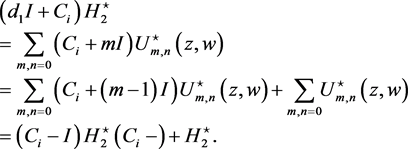 (72)
(72)
Next, let us operate with D on (5.1) on both sides, we obtain
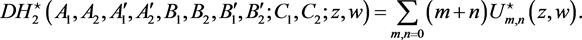 (73)
(73)
Hence, we can find that
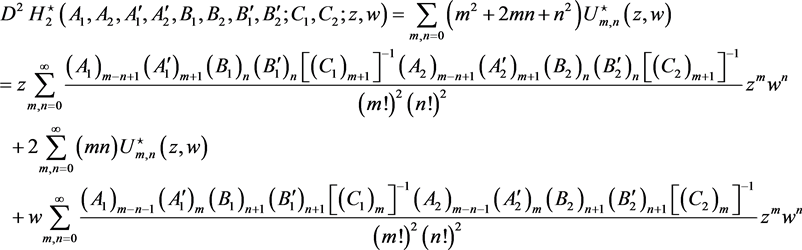
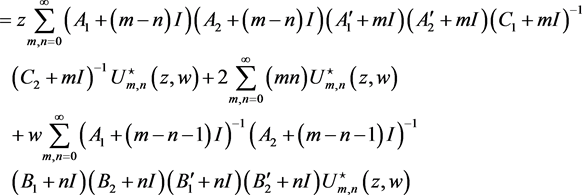

6. Conclusion
The results are established in this study to express a clear idea that the use of operational techniques provides a simple and straightforward method to get new relations for Horn matrix functions. Therefore, these results are considered original, variant, significant, interesting and capable to develop its study in the future.
Acknowledgements
1) The authors would like to thank the referees for their valuable comments and suggestions to improve the quality of the paper.
2) The third Author (Ayman Shehata) expresses his sincere appreciation to Dr. Mohammed Eltayeb Elffaki Elasmaa (Assistant Prof. Department of English language, Faculty of Arts and Human Studies, University of Dongola, Sudan) for his kinds interests, encouragements, help and correcting language errors for this paper.
Open Problem
The same class of new differential and integral operators can be used for the Horn matrix functions. Hence, new results and further applications can be obtained. Further applications will be discussed in a forthcoming paper.