Ion Nonthermality Induced Nonlinear Dust Acoustic Wave Propagation in a Complex Plasma in Presence of Weak Secondary Electron Emission from Dust Grains

Subrata Bhakta¹, Susmita Sarkar²

¹Department of Mathematics, S. A. Jaipuria College, Kolkata, India.
²Department of Applied Mathematics, University of Calcutta, Kolkata, India.

DOI: 10.4236/jmp.2018.95059                

Abstract

In this paper we have investigated the effect of ion nonthermality on nonlinear dust acoustic wave propagation in a complex plasma in presence of weak secondary electron emission from dust grains. Equilibrium dust charge in this case is negative. Dusty plasma under our consideration consists of inertialess nonthermal ions, Boltzman distributed primary and secondary electrons and negatively charged inertial dust grains. Both adiabatic and nonadiabatic dust charge variations have been taken into account. Our analysis shows that in case of adiabatic dust charge variation, at a fixed non-zero ion nonthermality increasing secondary electron emission decreases amplitude and increases width of the rarefied dust acoustic soliton whereas for a fixed secondary electron yield increasing ion nonthermality increases amplitude and decreases width of such rarefied dust acoustic soliton. Thus shape of the soliton may be retained if strength of both the secondary electron yield and the ion nonthermality are increased. Nonadiabatic dust charge variation shows that, at fixed non-zero ion nonthermality, increasing secondary electron emission suppresses oscillation of oscillatory dust acoustic shock at weak nonadiabaticity and pronounces monotonicity of monotonic dust acoustic shock at strong nonadiabaticity. On the other hand at a fixed value of the secondary electron yield, increasing ion nonthermality enhances oscillation of oscillatory dust acoustic shock at weak nonadiabaticity and reduces monotonicity of monotonic dust acoustic shock at strong nonadiabaticity. Thus nature of dust acoustic shock may also remain unchanged if both secondary electron yield and ion nonthermality are increased.

Keywords

Complex Plasma, Ion Nonthermality, Weak Secondary Electron Emission, Adiabaticity and Nonadiabaticity

1. Introduction

Dusty plasma has become an important field of plasma research since the last decade of the twentieth century. Such plasma consists of electrons, ions and massive charged dust grains which are commonly observed in space and astrophysical plasmas. These dust grains are charged by different mechanisms. They may be charged by plasma current, secondary electron emission effect, photo electric effect or by some other charging processes. Whether the dust grains are negatively or positively charged depends upon the grain charging mechanism. If the dust grains embedded in a plasma are charged by the flow of plasma current, equilibrium dust charge is negative. Positive equilibrium dust charge may exist if some electrons emit from dust grains. Secondary electron emission is an important dust charging process in dusty plasma where both negative and positive equilibrium dust charge exist [1] [2] [3] [4] .

When primary electrons impacting dust surfaces are energetic enough, they interact with the bulk material and loose energy due to many collisions. This consequently excites material electrons of dust grains. Some of those electrons ultimately leave the material surface and are called secondary electrons. Such secondary electrons have typical energies of few eV with Maxwellian like energy distribution. The secondary electron yield is defined as the average number of secondaries emitted from dust grains per unit incident primary electron. The maximum secondary electron yield and the corresponding maximum energy depend on the dust material. For weak secondary electron emission the secondary electron yield possesses low value and hence the equilibrium dust charge is negative whereas for strong secondary electron emission secondary yield value is high and the equilibrium dust charge is positive [1] [2] [3] . In this paper we are interested in negative equilibrium dust charge.

In most space and astrophysical environment electrons and ions are frequently nonthermal whose existences have been detected by several satellite observations. Nonthermal ions were observed by the Vella satellite from the earth’s bow shock [5] as well as in and around earth’s foreshock [6] . The Aspera experiment on Phobos-satellite detected nonthermal ion fluxes from the upper ionosphere of Mars [7] . Such space and astrophysical plasmas also contain huge dust grains which are charged by secondary electron emission mechanism where energetic electrons are present. Low frequency dust acoustic waves propagating in such plasmas are influenced by the nonthermality of background charge particles whose linear theory has already been studied [8] [9] [10] . Nonlinear theory considering positive equilibrium dust charge generated by secondary electron process has been recently reported [11] . In this paper we have investigated nonlinear theory of dust acoustic wave propagation considering the presence of nonthermal ions, Boltzmann distributed primary and secondary electrons and inertial dust grains having negative equilibrium dust charge. This negative equilibrium dust charge is a consequence of low secondary electron emission from dust grains. Study of this paper is important as we have seen [12] [13] opposite polarity of dust charge gives rise some opposite physical behaviour when the dust grains are charged by secondary electron mechanism. Thus to compare the nonlinear behaviour of dust acoustic waves with reference [11] where equilibrium dust charge was positive we have considered both adiabatic (fast) and nonadiabatic (slow) dust charge variation.

Nonlinear evolution of dust acoustic and dust ion acoustic waves in presence of adiabatic and non adiabatic dust charge variation were studied earlier by several authors considering grain charging by the flow of plasma current [14] - [23] . Effect of both weak (negative equilibrium dust charge) and strong (positive equilibrium dust charge) secondary electron emission in this nonlinear evolution process were later investigated with Boltzmann distributed electrons and ions [12] [13] . Presence of nonthermal ions along with positively charged dust gains generated by strong secondary electron emission has been recently reported [11] .

Our present analysis shows that in case of adiabatic dust charge variation, at a fixed non zero ion nonthermality, increasing secondary electron emission decreases amplitude and increases width of the rarefied dust acoustic soliton whereas for a fixed secondary electron yield, increasing ion nonthermality increases amplitude and decreases width of such rarefied dust acoustic soliton. This is opposite to the soliton behaviour when equilibrium dust charge is positive [11] where dust acoustic soliton is of compressive nature. Our present investigation also shows that in case of nonadiabatic dust charge variation for negative equilibrium dust charge, at fixed non zero ion nonthermality increasing secondary electron emission suppresses oscillation of oscillatory dust acoustic shock at weak nonadiabaticity and pronounces monotonicity of monotonic dust acoustic shock at strong nonadiabaticity. On the otherhand increasing ion nonthermality at fixed secondary electron yield in this case pronounces oscillation of oscillatory dust acoustic shock at weak nonadiabaticity and suppresses monotonicity of monotonic dust acoustic shock at strong nonadiabaticity. Thus behaviour of dust acoustic shock in both cases of weak and strong nonadiabaticity are opposite to their corresponding behaviour when equilibrium dust charge is positive [11] . But in both cases of negative and positive equilibrium dust charges shape of dust acoustic soliton which is rarefied for negative equilibrium dust charge and compressive for positive equilibrium dust charge remains unchanged if both ion nonthermality and secondary electron yield are increased. Similar behaviour shows for dust acoustic shock waves where in both cases of negative and positive equilibrium dust charges oscillation of oscillatory dust acoustic shock at weak nonadiabaticity and monotonicity of monotonic shock at strong nonadiabaticity remains unchanged if both ion nonthermality and secondary electron yield are increased.

2. Formulation of the Problem

For studying the effect of ion nonthermality on nonlinear one dimensional dust acoustic wave propagation in a complex plasma in presence of weak secondary electron emission we have considered a plasma consisting of inertialess nonthermal ions, Boltzman distributed primary and secondary electrons and negatively charged inertial dust grains satisfying the quasineutrality condition

$n_{io}=n_{eo}+n_{so}+z_{d0}{n}_{d0}$ . (1)

where $n_{io}$ , $n_{eo}$ , $n_{so}$ and $n_{do}$ are equilibrium number densities of ions, primary electrons, secondary electrons and dust grains respectively and $z_{do}$ is the number of charges on dust grains in equilibrium. The non dimensional number densities $N_i$ , $N_e$ and $N_s$ of nonthermal ions, Boltzmann distributed primary and secondary electrons are

$N_i=\left[1+\frac{4a}{1+3a}\left(\frac{\Phi }{{\sigma }_i}+\frac{{\Phi }^2}{{\sigma }_i{}^2}\right)\right]\exp \left(-\frac{\Phi }{{\sigma }_i}\right)$ (2)

$N_e=\exp \left(\Phi \right)$ . (3)

$N_s=\exp \left(\frac{\Phi }{{\sigma }_s}\right)$ (4)

where a is the ion nonthermal parameter, ${\sigma }_i=\frac{T_i}{T_e}$ and ${\sigma }_s=\frac{T_s}{T_e}$ are temperature ratios, $\Phi \left(=\frac{e\varphi }{T_e}\right)$ is the non dimensional electrostatic potential and $T_i,T_e$ and $T_s$ are ion, primary electron and secondary electron temperatures respectively.

Number density $N_d$ , velocity $V_d$ and charge $Q_d$ of dust grains obey the following non dimensional equations,

$\frac{\partial N_d}{\partial T}+\frac{\partial }{\partial X}\left(N_d{V}_d\right)=0$ (5)

$\frac{\partial V_d}{\partial T}+V_d\frac{\partial V_d}{\partial X}=-\frac{Q_d}{{\alpha }_d}\frac{\partial \Phi }{\partial X}$ (6)

$\left(\frac{{\omega }_{pd}}{{\nu }_d}\right)\left(\frac{\partial Q_d}{\partial T}+V_d\frac{\partial Q_d}{\partial X}\right)=\frac{1}{{\nu }_d}\left(\frac{{\bar{I}}_i+{\bar{I}}_e+{\bar{I}}_e^s}{z_{do}e}\right)$ (7)

All the above equations are closed if the electrostatic plasma potential F satisfies the Poisson equation,

$\begin{array}{c}\frac{{\partial }^2\Phi }{\partial X^2}=-\frac{1}{1+\frac{{\delta }_i}{{\sigma }_i}+\frac{{\delta }_s}{{\sigma }_s}}[{\delta }_i\left\{1+\frac{4a}{1+3a}\left(\frac{\Phi }{{\sigma }_i}+\frac{{\Phi }^2}{{\sigma }_i{}^2}\right)\right\}\exp \left(-\frac{\Phi }{{\sigma }_i}\right)-\exp \left(\Phi \right)\\ +{\delta }_s\exp \left(\frac{\Phi }{{\sigma }_s}\right)+\left({\delta }_i-{\delta }_s-1\right)Q_d{N}_d]\end{array}$ (8)

where ${\alpha }_d=\frac{{\delta }_i-{\delta }_s-1}{\frac{{\delta }_i}{{\sigma }_i}+\frac{{\delta }_s}{{\sigma }_s}+1},{\delta }_i=\frac{n_{i0}}{n_{e0}}$ and ${\delta }_s=\frac{n_{s0}}{n_{e0}}$ are number density ratios, ${\omega }_{pd}={\left(\frac{4\text{π}{n}_{d0}{z}_{d0}^2{e}^2}{m_d}\right)}^{1/2}$ and ${\nu }_d$ are the dust plasma frequency and dust charging

frequency, $m_d$ is the dust mass and X, T are non dimensional space and time variables.

Here,

$\begin{array}{l}{\bar{I}}_i=\text{π}{r}_0{}^{2}e\sqrt{\frac{8T_i}{\text{π}{m}_i}}\frac{n_{i0}}{1+3a}[\left\{\left(1+\frac{24a}{5}\right)+\frac{16a\Phi }{3{\sigma }_i}+\frac{4a{\Phi }^2}{{\sigma }_i{}^2}\right\}\\ -\frac{z{Q}_d}{{\sigma }_i}\left(1+\frac{8a}{5}+\frac{8a\Phi }{3{\sigma }_i}+\frac{4a{\Phi }^2}{{\sigma }_i{}^2}\right)]\exp \left(-\frac{\Phi }{{\sigma }_i}\right)\end{array}$ (9)

is the nonthermal ion current when equilibrium dust charge is negative [24] . The nonthermal ion density $N_i$ and nonthermal ion current ${\bar{I}}_i$ have been calculated with the help of the following nonthermal ion velocity distribution [25] ,

$\begin{array}{l}{F}_i\left(v_i\right)=F_i\left(v_x,v_y,v_z\right)\\ =\frac{n_{i0}}{1+3a}{\left(\frac{1}{2\text{π}{v}_{ti}^2}\right)}^{3/2}\left[1+4a{\left(\frac{1}{2}\frac{v_x^2}{v_{ti}^2}+\frac{\Phi }{{\sigma }_i}\right)}^2\right]\exp \left(-\frac{v_x^2+v_y^2+v_z^2}{2v_{ti}^2}-\frac{\Phi }{{\sigma }_i}\right)\end{array}$ .(10)

where $v_{ti}$ is the ion thermal velocity and $v_x,v_y,v_z$ are x, y, and z components of ion velocity.

Other current expressions are,

${\bar{I}}_e=-\text{π}{r}_0{}^{2}e\sqrt{\frac{8T_e}{\text{π}{m}_e}}{n}_{e0}\exp \left(\Phi \right)\left(z{Q}_d\right)$ . (11)

${\bar{I}}_e{}^s=3.7{\delta }_M\text{π}{r}_0{}^{2}e\sqrt{\frac{8T_e}{\text{π}{m}_e}}{n}_{e0}\exp \left(\Phi +z{Q}_d\right)F_5\left(\frac{E_M}{4T_e}\right)$ (12)

where $z=z_{d0}{e}^2/r_0{T}_e$ , $r_0$ is the grain radius, ${\delta }_M$ is the maximum secondary electron yield, $m_e$ is the electron mass and the function $F_5\left(x\right)$ is given by [1] ,

$F_5\left(x\right)=x^2{\displaystyle {\int }_0^{\infty }{u}^5\exp \left[-\left(x{u}^2+u\right)\right]\text{d}u}$ and $x=\frac{E_M}{4T_e}$ (12a)

Value of ${\delta }_M$ is low for weak secondary electron emission and high for strong secondary electron emission. Thus for weak secondary electron emission equilibrium dust charge is negative and for strong secondary electron emission equilibrium dust charge is positive.

The primary electron, secondary electron, ion and dust number densities $n_e$ , $n_s$ , $n_i$ , $n_d$ , dust fluid velocity $u_d$ , electrostatic potential energy ef, dust charge $q_d$ and the independent space, time variables x, t are nondimensionalized here in the following way,

$\begin{array}{l}{N}_e=n_e/n_{e0};N_s=n_s/n_{s0};N_i=n_i/n_{i0};N_d=n_d/n_{d0};V_d=u_d/c_d;\\ \Phi =\frac{e\varphi }{T_e};Q_d=q_d/e{z}_{d0};q_{do}=-z_{do}e;X=x/{\lambda }_d;T={\omega }_{pd}t\end{array}$ (13)

where ${\lambda }_D={\left(\frac{T_{eff}}{4\text{π}{z}_{d0}{n}_{d0}{e}^2}\right)}^{1/2}$ is the dusty plasma Debye length and $c_d=\sqrt{\frac{z_{d0}{T}_{eff}}{m_d}}$ is the dust acoustic speed. The effective temperature $T_{eff}$ is defined by

$\frac{1}{T_{eff}}=\frac{1}{z_{do}{n}_{do}}\left(\frac{n_{eo}}{T_e}+\frac{n_{so}}{T_s}+\frac{n_{io}}{T_i}\right)$ (14)

The grain charging frequency in this case has been calculated in the form,

${\nu }_d=-{\frac{\partial \left({\bar{I}}_i+{\bar{I}}_e+{\bar{I}}_e^s\right)}{\partial Q_d}|}_{Q_d=-z_{d}e}=\frac{r_0}{\sqrt{2\text{π}}}\frac{{\omega }_{pi}^2}{V_{thi}}\left(\frac{5+8a}{5\left(1+3a\right)}\right)\left[1+z+{\sigma }_i\left(\frac{5+24a}{5+8a}\right)\right]$ (15)

The equilibrium current balance equation ${\bar{I}}_i+{\bar{I}}_e+{\bar{I}}_e^s=0$ gives

${\delta }_i=\sqrt{\frac{m_e^i}{{\sigma }_i}}\exp \left(-z\right){\alpha }_{1s}\frac{5\left(1+3a\right)}{\left[\left(5+24a\right)+\frac{z}{{\sigma }_i}\left(5+8a\right)\right]}$ , ${\alpha }_{1s}=1-3.7{\delta }_M{F}_5\left(\frac{E_M}{4T_e}\right)$ (16)

This ${\delta }_i$ must be greater than 1 to satisfy the quasi neutrality condition (1).

3. Reductive Perturbation Analysis: Adiabatic and Nonadiabatic Dust Charge Variation

For the study of small amplitude structures in dusty plasma in presence of weak secondary electron emission, we employ the reductive perturbation technique, using the stretched coordinates $\xi ={\epsilon }^{1/2}\left(X-\lambda T\right)$ and $\tau ={\epsilon }^{3/2}T$ where e is a small parameter and l is the wave velocity normalized by $c_d$ . The variables $N_d,V_d,\Phi$ and $Q_d$ are then expanded as,

$\begin{array}{l}{N}_d=1+\epsilon N_{d1}+{\epsilon }^2{N}_{d2}+\cdots ,V_d=\epsilon V_{d1}+{\epsilon }^2{V}_{d2}+\cdots \\ \Phi =\epsilon {\Phi }_1+{\epsilon }^2{\Phi }_2+\cdots ,Q_d=-1+\epsilon Q_{d1}+{\epsilon }^2{Q}_{d2}+{\epsilon }^3{Q}_{d3}+\cdots \end{array}$ (17)

Substituting these expansions into Equations (2)-(8) with (9), (11), (12) and collecting the terms of different powers of e we obtain,

$\lambda N_{d1}=V_{d1},V_{d1}=-\frac{{\Phi }_1}{\lambda {\alpha }_d},N_{d1}=-\frac{{\Phi }_1}{{\lambda }^2{\alpha }_d},{\Phi }_1+{\alpha }_d\left(N_{d1}-Q_{d1}\right)=0$ (18)

$\frac{\partial N_{d1}}{\partial \tau }-\lambda \frac{\partial N_{d2}}{\partial \xi }+\frac{\partial }{\partial \xi }\left(N_{d1}{V}_{d1}\right)+\frac{\partial V_{d2}}{\partial \xi }=0$ (19)

$\frac{\partial V_{d1}}{\partial \tau }-\lambda \frac{\partial V_{d2}}{\partial \xi }+V_{d1}\frac{\partial V_{d1}}{\partial \xi }=\frac{1}{{\alpha }_d}\left(\frac{\partial {\Phi }_2}{\partial \xi }-Q_{d1}\frac{\partial {\Phi }_1}{\partial \xi }\right)$ (20)

$\frac{{\partial }^2{\Phi }_1}{\partial {\xi }^2}=P{\Phi }_2+{\alpha }_d{N}_{d2}-{\alpha }_d{Q}_{d2}+R{\Phi }_1^2$ (21)

where $P=\frac{\frac{{\delta }_i}{{\sigma }_i}\left(\frac{1-a}{1+3a}\right)+\frac{{\delta }_s}{{\sigma }_s}+1}{\frac{{\delta }_i}{{\sigma }_i}+\frac{{\delta }_s}{{\sigma }_s}+1}$ and $R=\left[\frac{1}{{\lambda }^2}\left(\frac{1}{{\alpha }_a}-\frac{1}{{\alpha }_d{\lambda }^2}\right)-\frac{1}{2}\frac{\left(\frac{{\delta }_i}{{\sigma }_i^2}-\frac{{\delta }_s}{{\sigma }_s^2}-1\right)}{\left(\frac{{\delta }_i}{{\sigma }_i}+\frac{{\delta }_s}{{\sigma }_s}+1\right)}\right].$

In case of adiabatic dust charge variation dust grains are charged in fast time scale. Hence dust charging frequency ${\nu }_d$ is very high compared to dust plasma

frequency. With this approximation $\frac{{\omega }_{pd}}{{\nu }_d}\approx 0$ which reduces (7) to,

${\bar{I}}_i+{\bar{I}}_e+{\bar{I}}_e^s=0$ (22)

Equating from its both sides the terms containing e and ${\epsilon }^2$ , we get $Q_{d1}$ and $Q_{d2}$ in the following form,

$Q_{d1}=-{\beta }_d{\Phi }_1$ , $Q_{d2}=-{\beta }_d{\Phi }_2+{\gamma }_d{\Phi }_1^2$ (23)

where

$\begin{array}{l}{\beta }_d=\frac{{\beta }_b}{z{\beta }_a};{\beta }_a=\sqrt{\frac{m_e^i}{{\sigma }_i}}{\alpha }_{1s}+\frac{5+8a}{5\left(1+3a\right)}\frac{{\delta }_i}{{\sigma }_i};\\ {\beta }_b=\sqrt{\frac{m_e^i}{{\sigma }_i}}{\alpha }_{1s}{\text{e}}^{-z}+\frac{{\delta }_i}{{\sigma }_i\left(1+3a\right)}\left\{1-\frac{8a}{15}+\frac{z}{{\sigma }_i}\left(1-\frac{16a}{15}\right)\right\}\text{and}{\gamma }_d=\frac{{\gamma }_c}{z{\beta }_a};\\ {\gamma }_c={\gamma }_{c1}+{\gamma }_{c2}+{\gamma }_{c3};{\gamma }_{c1}=\left[\frac{{\delta }_i}{\left(1+3a\right){\sigma }_i^2}\left\{\frac{1}{2}-\frac{16a}{15}+\frac{z}{{\sigma }_i}\left(\frac{1}{2}+\frac{32a}{15}\right)\right\}-\sqrt{\frac{m_e^i}{{\sigma }_i}}{\alpha }_{1s}{\text{e}}^{-z}\right];\\ {\gamma }_{c2}=\left[\sqrt{\frac{m_e^i}{{\sigma }_i}}{\alpha }_{1s}-\frac{{\delta }_i}{\left(1+3a\right){\sigma }_i^2}\left(1-\frac{16a}{15}\right)\right]\left(z{\beta }_d\right);{\gamma }_{c3}=\left[-0.5\sqrt{\frac{m_e^i}{{\sigma }_i}}{\alpha }_{1s}\right]{\left(z{\beta }_d\right)}^2\\ \lambda =\frac{1}{\sqrt{P+{\alpha }_d{\beta }_d}},m_e^i=\frac{m_i}{m_e}.\end{array}$ (24)

Eliminating all the second-order terms from Equations (18)-(21) and (23) we get the KdV equation

$\frac{\partial {\Phi }_1}{\partial \tau }+A{\Phi }_1\frac{\partial {\Phi }_1}{\partial \xi }+B\frac{{\partial }^3{\Phi }_1}{\partial {\xi }^3}=0$ (25)

where, $A=B\left[\frac{\left(\frac{{\delta }_i}{{\sigma }_i^2}-\frac{{\delta }_s}{{\sigma }_s^2}-1\right)}{\left(\frac{{\delta }_i}{{\sigma }_i}+\frac{{\delta }_s}{{\sigma }_s}+1\right)}+2{\alpha }_d{\gamma }_d-\frac{3P}{{\lambda }^2{\alpha }_d}\right]$ , $B=\frac{{\lambda }^3}{2}=\frac{1}{2}{\left(P+{\alpha }_d{\beta }_d\right)}^{-3/2}$ (26)

On transforming to the wave frame $\eta =\xi -M\tau$ , the travelling wave solution

of equation (25) can be written as 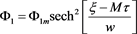which represents a soliton with amplitude and width. M is the Mach

number.

In case of nonadiabatic dust charge variation dust grains are charged in comparatively slow time scale so that dust charging frequency 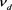is not very high

compared to dust plasma frequency. With this approximation is small but finite. We assume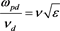, where e is small and n is of order unity [17] .

With this assumption, Equation (7) along with expansion (17) give the following first and second order dust charge fluctuation

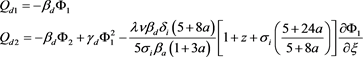(27)

Eliminating all the second-order terms of Equation (18)-(21) and (27) we get the standard KdV-Burger equation,

. (28)

where 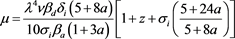is the Berger coefficient

arising due to nonadiabaticity of dust charge variation. Here all A, B, and m depend on both ion nonthermality parameter a and maximum secondary electron yield. Value of is low as we are considering weak secondary electron emission.

4. Numerical Estimation

In this section we have drawn different graphs to show the effect of ion nonthermality on nonlinear dust acoustic wave propagation for both adiabatic and non adiabatic dust charge variation when equilibrium dust charge generated by weak secondary electron emission is negative. For numerical estimation, we have considered [1] [26] , , 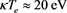, , 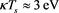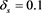and Al₂O₃ dust for which lies in the range 2 - 9.

From Figure 1 and Figure 2 we have seen that at a fixed non zero ion nonthermality increasing secondary electron emission decreases amplitude and increases width of the rarefied dust acoustic soliton whereas for a fixed secondary electron yield increasing ion nonthermality increases amplitude and decreases width of such rarefied dust acoustic soliton in case of adiabatic dust charge variation. This is opposite to the behaviour of the compressive dust acoustic soliton where ions are nonthermal and equilibrium dust charge is positive [11] . In both cases shape of the soliton remains unchanged but in opposite sense if strength of both the secondary electron yield and the ion nonthermality are increased.

In case of nonadiabatic dust charge variation Figure 3 and Figure 4 show that for both weak (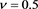) and strong () nonadiabaticity at fixed nonzero ion nonthermality increasing secondary electron emission increases magnitude of the ratio which implies dissipation is stronger than dispersion. As a

Figure 1. Plot of the rarefied Dust Acoustic Soliton for different δ_M at a = 0.2 in case of adiabatic dust charge variation.

Figure 2. Plot of the rarefied Dust Acoustic Soliton for different a at δ_M = 4 in case of adiabatic dust charge variation.

consequence increasing secondary electron emission suppresses oscillation of dust acoustic shock when it is oscillatory at weak nonadiabaticity and pronounces monotonicity when it is monotonic at strong nonadiabaticity. This is clear from Figure 5 and Figure 6. Similarly Figure 7 and Figure 8 show that for both weak and strong nonadiabaticity at a fixed value of the secondary electron yield, increasing ion nonthermality decreases magnitude of the ratio which means dispersion becomes stronger in this case than dissipation. Thus at a fixed value of secondary electron yield, increasing ion nonthermality

Figure 3. Plot of the ratio μ/B versus z for different δ_M at a = 0.2 and ν = 0.5 in case of nonadiabatic dust charge variation.

Figure 4. Plot of the ratio μ/B versus z for different δ_M at a = 0.2 andν = 5.0 in case of nonadiabatic dust charge variation.

pronounces oscillation of the dust acoustic shock at weak () nonadiabaticity and reduces monotonicity at strong () nonadiabaticity. It is clear from Figure 9 and Figure 10. Thus nature of the dust acoustic shock may remain unchanged if both secondary electron yield and ion nonthermality are increased. This behaviour is opposite of the behaviour of the dust acoustic shock when ions are nonthermal and equilibrium dust charge is positive [11] . This opposite nature is due to the opposite polarity of dust charge.

5. Conclusions

In this paper we have studied the effect of ion nonthermality on nonlinear dust

Figure 5. Oscillatory shock wave for different values of δ_M at a = 0.2 and ν = 0.5 in case of nonadiabatic dust charge variation.

Figure 6. Monotonic shock wave for different values of δ_M at a = 0.2 and ν = 5.0 in case of nonadiabatic dust charge variation.

acoustic wave propagation in a complex plasma where dust grains are charged by secondary electron emission process. Strength of secondary electron emission has been assumed weak. As a consequence dust grains are negatively charged. Both adiabatic and nonadiabatic dust charge variations have been considered. Analysis shows that adiabatic dust charge variation generates dust acoustic soliton whose amplitude and width both depend on the nonthermal parameter a and the secondary electron yield. For fixed ion nonthermality, increasing secondary electron yield decreases amplitude and increases width of the rarefied

Figure 7. Plot of the ratio μ/B versus z for different a at δ_M = 4 and ν = 0.5 in case of nonadiabatic dust charge variation.

Figure 8. Plot of the ratio μ/B versus z for different a at δ_M = 4 andν = 5.0 in case of nonadiabatic dust charge variation.

dust acoustic soliton whereas for a fixed secondary electron yield, increasing ion nonthermality increases its amplitude and decreases its width.

For nonadiabatic dust charge variation at a fixed nonzero ion nonthermality, increasing secondary electron emission suppresses oscillation of the oscillatory dust acoustic shock at weak nonadiabaticity and pronounces monotonicity of monotonic dust acoustic shock at strong nonadiabaticity. On the other hand at a fixed secondary electron yield, increasing ion nonthermality pronounces oscillation of oscillatory dust acoustic shock at weak nonadiabaticity and suppresses monotonicity of monotonic dust acoustic shock at a strong nonadiabaticity. Thus behaviour of dust acoustic soliton and dust acoustic shock may

Figure 9. Oscillatory shock wave for different values of a at δ_M = 4 and ν = 0.5 in case of nonadiabatic dust charge variation.

Figure 10. Monotonic shock wave for different values of a at δ_M = 4 and ν = 5.0 in case of nonadiabatic dust charge variation.

remain unchanged if both ion nonthermality and secondary electron yield are increased.

The results of the present investigation with negative equilibrium dust charge and the investigation of reference [11] with positive equilibrium dust charge show opposite evolution character of dust acoustic soliton and dust acoustic shock due to opposite polarity of dust charge. But in both cases nature of dust acoustic soliton and dust acoustic shock remains unaffected if both ion nonthermality and secondary electron yield are increased.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Meyer-Vernet, N. (1982) Astronomy & Astrophysics, 105, 98.
[2]	Whipple, E.C. (1981) Reports on Progress in Physics, 44, 1197. https://doi.org/10.1088/0034-4885/44/11/002
[3]	Horanyi, M. (1996) Annual Review of Astronomy and Astrophysics, 34, 383-418. https://doi.org/10.1146/annurev.astro.34.1.383
[4]	Hachenberg, O. and Brauer, W. (1959) Advances in Electronics and Electron Physics, 11, 413-499. https://doi.org/10.1016/S0065-2539(08)60999-3
[5]	Asbridge, J.R., Bame, S.J. and Strong, I.B. (1968) Journal of Geophysical Research, 73, 5777. https://doi.org/10.1029/JA073i017p05777
[6]	Feldman, W.C., Anderson, S.J., Bame, J., et al. (1983) Journal of Geophysical Research, 88, 96. https://doi.org/10.1029/JA088iA01p00096
[7]	Ludin, R., Zakharov, A., Pellimen, R., et al. (1989) Nature (London), 341, 609-612. https://doi.org/10.1038/341609a0
[8]	Sarkar, S., Maity, S. and Banerjee, S. (2011) Physicas Scripta, 84, Article ID: 045501. https://doi.org/10.1088/0031-8949/84/04/045501
[9]	Sarkar, S. and Maity, S. (1997) Physics of Plasmas, 4, 253. https://doi.org/10.1063/1.872086
[10]	Sarkar, S. and Bhakta, S. (2016) Journal of Modern Physics, 7, 74-86. https://doi.org/10.4236/jmp.2016.71008
[11]	Bhakta, S. and Sarkar, S. (2017) AIP Advances, 7, Article ID: 075113. https://doi.org/10.1063/1.4985747
[12]	Bhakta, S., Ghosh, U. and Sarkar, S. (2017) Physics of Plasmas, 24, Article ID: 023704. https://doi.org/10.1063/1.4976711
[13]	Bhakta, S. and Sarkar, S. (2017) Physics of Plasmas, 24, Article ID: 073706. https://doi.org/10.1063/1.4990553
[14]	Xie, B.S., He, K.F. and Huang, Z.Q. (1998) Physics Letters A, 247, 403-409. https://doi.org/10.1016/S0375-9601(98)00616-1
[15]	Duan, W.-S. (2004) Chinese Physics, 13, 5. https://doi.org/10.1088/1009-1963/13/1/002
[16]	Elwakil, S.A., Zahran, M.A., El-Shewy, E.K. and Mowafy, A.E. (2011) Advances in Space Research, 48, 1067-1075. https://doi.org/10.1016/j.asr.2011.04.034
[17]	Chen, J.-H. and Wei, N.-X. (2009) Communications in Theoretical Physics, 51, 524-528. https://doi.org/10.1088/0253-6102/51/3/29
[18]	Xie, B., He, K. and Huang, Z. (1998) Chinese Physics Letters, 15, 12.
[19]	Gupta, M.R., Sarkar, S., Ghosh, S., Debnath, M. and Khan, M. (2001) Physical Review E, 63, Article ID: 046406.
[20]	Ghosh, S., Sarkar, S., Khan, M. and Gupta, M.R. (2001) IEEE Transactions on Plasma Science, 29, 409.
[21]	Ghosh, S., Sarkar, S., Khan, M., Avinash, K. and Gupta, M.R. (2003) Physics of Plasmas, 10, 977-983. https://doi.org/10.1063/1.1555621
[22]	Wang, Y., Guo, C., Jiang, X., Zhou, Z. and Ni, X. (2010) Physics of Plasmas, 17, Article ID: 113701. https://doi.org/10.1063/1.3504223
[23]	Wang, Y., Guo, X., Lu, Y. and Wang, X. (2016) Physics Letters A, 380, 215-221. https://doi.org/10.3847/1538-4357/834/1/38
[24]	Ghosh, S., Bharuthram, R., Khan, M. and Gupta, M.R. (2004) Physics of Plasmas, 11, 3602. https://doi.org/10.1063/1.1760584
[25]	Cairns, R.A., Bingham, R., Dendy, R.O., Nairn, C.M.C., Shukla, P.K. and Mamun, A.A. (1995) Journal de Physique IV, 5, C6-C43. https://doi.org/10.1051/jp4:1995608
[26]	Goertz, C.K. (1989) Reviews of Geophysics, 27, 271.