On the Extension of the Three-Term Recurrence Relation to Probabilities Distributions without Moments ()
1. Introduction
It has been known from [1] and [2] that for every probability distribution 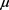 with finite moments of all orders, there exits a family of monic orthogonal polynomials
with finite moments of all orders, there exits a family of monic orthogonal polynomials 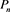 and a paire of sequences
and a paire of sequences 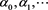 and
and 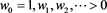 satisfying the three-term recurrence relation (or the tri-diagonal Jacobi relation)
satisfying the three-term recurrence relation (or the tri-diagonal Jacobi relation)
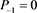 (1)
(1)
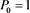 (2)
(2)
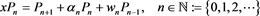 (3)
(3)
The sequences (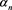 ) and (
) and (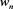 ) are called the Szego-Jacobi parameters of
) are called the Szego-Jacobi parameters of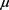 .
.
The starting point of the quantum probabilistic approach to the theory of orthogonal polynomials (OP) is an operator interpretation of the tri-diagonal Jacobi relation (3) in terms of Creation, Annihilation and Preservation (CAP) operators. This allows to associate, in a canonical way, to any random variable with all moments commutation relations that generalize the Heisenberg commutation relations (corresponding to the Gauss-Poisson class). From the mathematical point of view, this approach has led to some new results in the theory of OP.
In order to give this operator interpretation, we shall recall the notion of the interacting Fock probability space associated with the measure 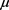 (See [3] for more details).
(See [3] for more details).
Consider an infinite-dimensional separable Hilbert space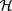 , in which a complete orthonormal basis
, in which a complete orthonormal basis 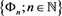 is chosen. Let
is chosen. Let 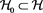 denote the dense subspace spanned by the complete orthonormal basis
denote the dense subspace spanned by the complete orthonormal basis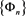 .
.
Given the sequence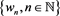 , we associate linear operators
, we associate linear operators ![]() given by:
given by:
![]()
![]()
Its known that ![]() are mutually adjoint and the linear subspace
are mutually adjoint and the linear subspace ![]() spanned by the set
spanned by the set ![]() is invariant under the action of
is invariant under the action of![]() .
.
The quadruple ![]() is called the interacting Fock probability space associated with
is called the interacting Fock probability space associated with![]() . The operators
. The operators ![]() and
and ![]() are called the creation operator and the annihilation operators respectively. The linear operator given by
are called the creation operator and the annihilation operators respectively. The linear operator given by
![]()
is called the number operator. More generally, with the sequence![]() , we associate the preservation operator
, we associate the preservation operator ![]() by the prescription
by the prescription
![]()
Let ![]() be the space of classes of complex valued, square integrable functions w.r.t
be the space of classes of complex valued, square integrable functions w.r.t![]() . In the following, we simply denote it by
. In the following, we simply denote it by ![]() and we assume that the sub-space
and we assume that the sub-space ![]() spanned by the polynomial functions is dense in
spanned by the polynomial functions is dense in![]() . So that
. So that ![]() is an Hilbertian basis of
is an Hilbertian basis of![]() . In such case, we consider the isomorphism U from
. In such case, we consider the isomorphism U from ![]() to
to ![]() whose its restriction on
whose its restriction on ![]() given by:
given by:
![]()
where![]() . Then the U is unitary and we have
. Then the U is unitary and we have
![]()
![]()
![]()
![]()
![]()
![]()
This means that the field operator ![]() is the
is the ![]() -image of the position operator
-image of the position operator ![]() on
on ![]() providing, in this way, a new interpretation of the recursion relation driving by OP in term of CAP operators. Since the random variable with distribution
providing, in this way, a new interpretation of the recursion relation driving by OP in term of CAP operators. Since the random variable with distribution ![]() can be identified, up to stochastic equivalence
can be identified, up to stochastic equivalence![]() , with the position operator q on
, with the position operator q on![]() , the previous new formulation of the tri-diagonal Jacobi relation in term of the CAP operators is called the quantum decomposition of the classical random variable. In fact we have seen that
, the previous new formulation of the tri-diagonal Jacobi relation in term of the CAP operators is called the quantum decomposition of the classical random variable. In fact we have seen that
![]()
This shows that any classical random variable has a built in non commutative structure which is intrinsic and canonical, and not artificially put by hands, that is a sum of three non commuting random variables.
This result motivated the apparition of a series of papers [4] - [9] dealing in the same context and provided many applications in the theory of quantum probability. In the paper [4] , a similar result was obtained but for the family of random variables having an infinitely divisible distribution (I.D-distribution in the following) and having only the moment of the second order. Here, similarity means that the quantum decomposition can be obtained also for this family of random variables.
Based on the notion of the positive definite kernel and using the Lévy-Khintchine function established for the I.D-distributions, the paper [4] constructed a natural isomorphism U from the Fock space ![]() over the
over the ![]() -space w.r.t the Lévy measure
-space w.r.t the Lévy measure ![]() to the space
to the space![]() . Then the
. Then the ![]() -image of the position operator q is the field operator
-image of the position operator q is the field operator
![]() (4)
(4)
where ![]() is the function
is the function![]() . See papers [10] and [11] in which the operator Q was widely studied.
. See papers [10] and [11] in which the operator Q was widely studied.
In this approach, the construction was not based on the orthogonal polynomials sequence associated with![]() . But it required only the infinite divisibility property, where the Lévy-Khinchine function have played an important role. Then one can ask about the analytic form of the relation (4), or equivalently the counterpart of the three-term recurrence relation. The only obscure point is the existence of such an analogue of the sequence of the orthogonal polynomials. Since the hypothesis on moments is not satisfied, such a sequence of orthogonal polynomial does exist. But the isomorphism U provided us a such chaos-decomposition of the space
. But it required only the infinite divisibility property, where the Lévy-Khinchine function have played an important role. Then one can ask about the analytic form of the relation (4), or equivalently the counterpart of the three-term recurrence relation. The only obscure point is the existence of such an analogue of the sequence of the orthogonal polynomials. Since the hypothesis on moments is not satisfied, such a sequence of orthogonal polynomial does exist. But the isomorphism U provided us a such chaos-decomposition of the space![]() . For this reason we ask the question if there exist a such analogue for the family of orthogonal polynomial, if it is the case it must be a total family of orthogonal functions in the space
. For this reason we ask the question if there exist a such analogue for the family of orthogonal polynomial, if it is the case it must be a total family of orthogonal functions in the space ![]() satisfying a recursion relation similar to the well known for OP.
satisfying a recursion relation similar to the well known for OP.
This paper is organized as follows:
In Section 2, we recall some known facts about the bosonic Fock space and the quantum decomposition of classical random variables without moments, having I.D-distributions, obtained in [12] [4] and [5] . In Section 3, we compute the action of the generalized field operator ![]() on the nth particle vectors (
on the nth particle vectors (![]() ). The main result of this paper will be given in Section 4, so that we compute the action of the position operator
). The main result of this paper will be given in Section 4, so that we compute the action of the position operator ![]() on the orthogonal functions
on the orthogonal functions![]() . This provide such a generalization of the tri-diagonal recursion relation for OP. Finally, the explicit form of theses functions will be given.
. This provide such a generalization of the tri-diagonal recursion relation for OP. Finally, the explicit form of theses functions will be given.
2. Preliminaries
2.1. The Bosonic Fock Space
Let ![]() be a separable Hilbert space. Let us denote
be a separable Hilbert space. Let us denote ![]() (resp.
(resp.![]() ) the tensor product of n-copies of
) the tensor product of n-copies of ![]() (resp.
(resp.![]() ) and let
) and let ![]() be the unique unitary operator such that
be the unique unitary operator such that
![]()
where ![]() is a permutation of n-variables.
is a permutation of n-variables.
Let![]() , were
, were ![]() is the vacuum vector, let
is the vacuum vector, let
![]()
be the orthogonal projection.
We define
![]()
where![]() .
.
Let us denote
![]()
Then![]() . Moreover, the set
. Moreover, the set ![]() is linearly independent dense in
is linearly independent dense in![]() .
.
The bosonic creation and annihilation operators are defined, on the total set
![]()
as follows:
For![]() ,
,
![]()
![]() (5)
(5)
and
![]()
![]()
![]() (6)
(6)
and
![]()
where ![]() denotes omission of the corresponding variable. The preservation operator associated with the self adjoint operator T on
denotes omission of the corresponding variable. The preservation operator associated with the self adjoint operator T on ![]() is given by:
is given by:
![]() (7)
(7)
2.2. The Quantum Decomposition of Classical Random Variables with I.D-Distributions
In this section, we recall briefly, what has been obtained in the paper [4] around quantum decomposition of random variables with I.D-distributions and having a finite second order moment.
Let us consider a random variable X with I.D-probability distribution ![]() having a finite second order moment. It is known (see [13] ), that the Fourier transform of
having a finite second order moment. It is known (see [13] ), that the Fourier transform of ![]() given by
given by
![]() (8)
(8)
where ![]() is given by
is given by
![]() (9)
(9)
such that ![]() and
and ![]() is the the Lévy measure of
is the the Lévy measure of![]() . The function
. The function ![]() is called the Lévy-Khintchine function or the characteristic exponent associated with
is called the Lévy-Khintchine function or the characteristic exponent associated with![]() .
.
Since the second order moment of ![]() is finite, the same result will be true for
is finite, the same result will be true for![]() , i.e,:
, i.e,:
![]() (10)
(10)
We suppose also that the gaussian part of ![]() is null (i.e.,
is null (i.e.,![]() ). Under these conditions, we have the following results:
). Under these conditions, we have the following results:
The family ![]() of the trigonometric functions is total in
of the trigonometric functions is total in ![]() and the family of the functions
and the family of the functions
![]() (11)
(11)
is total in![]() .
.
Then by applying the Araki-Woods-Parthasarathy-Schmidt isomorphism in [12] for the infinitely divisible positive definite kernel
![]()
we have proved the following theorem (See [4] for more details and descriptions).
Theorem 2.1. The unique linear operator U given on the exponential vectors ![]() by:
by:
![]()
![]() (12)
(12)
is an unitary isomorphism from the Fock space ![]() to
to![]() .
.
Definition 1. Let q be the multiplication (position) operator in![]() :
:
![]()
Define the operator Q on ![]() by
by
![]()
where U is the isomorphism defined by (12). Since ![]() is a finite measure on
is a finite measure on![]() , the operator q is self-adjoint (see [14] Proposition 1, chapter VIII. 3) and
, the operator q is self-adjoint (see [14] Proposition 1, chapter VIII. 3) and
![]()
The operator Q is called the generalized field operator.
It follows from condition (10) that the total set ![]() is in the domain of Q. Moreover, one has the following theorem:
is in the domain of Q. Moreover, one has the following theorem:
Theorem 2.2. Let ![]() be the function given by
be the function given by
![]()
Then the generalized field operator Q takes the form
![]() (13)
(13)
where![]() , the expectation of X, and
, the expectation of X, and ![]() are the creation, annihilation and preservation operators in the Fock space
are the creation, annihilation and preservation operators in the Fock space ![]() given by the prescriptions as in (5)-(7).
given by the prescriptions as in (5)-(7).
3. The Generalized Field Operator
3.1. Notations
We denote by ![]() the set of all sequences of non negatives integers with finite number of nonzero entries. In the sequel
the set of all sequences of non negatives integers with finite number of nonzero entries. In the sequel ![]() (resp.
(resp.![]() ) will be interpreted as subset of the set
) will be interpreted as subset of the set ![]() (resp.
(resp.![]() ). Throughout the remain of this paper we shall use the following notations:
). Throughout the remain of this paper we shall use the following notations:
For ![]() and
and ![]() ,
,
![]()
![]()
The support of such element ![]() is defined by
is defined by
![]()
When ![]() is a sequence of elements of an Hilbert space
is a sequence of elements of an Hilbert space ![]() and
and![]() , we denote
, we denote
![]()
In particular if ![]() and
and![]() , so that
, so that ![]() takes the form
takes the form
![]()
then
![]()
From [15] , we recall the following identity which is the analogue of the multinomial Newton formula
![]() (14)
(14)
which take place whenever the series ![]() is convergent.
is convergent.
If ![]() is separable and
is separable and ![]() is an Hilbertian basis of it, then the set
is an Hilbertian basis of it, then the set
![]()
is an orthonormal basis of the Hilbert space![]() , with the convention
, with the convention![]() .
.
Let ![]() be the canonic basis of
be the canonic basis of![]() . For
. For![]() , we denote
, we denote
![]() (15)
(15)
and
![]() (16)
(16)
Note that if![]() , then
, then ![]() can be defined as in (16), however it is not an element of
can be defined as in (16), however it is not an element of![]() , because its kth-entry
, because its kth-entry![]() . In this case, we adapt by convention that
. In this case, we adapt by convention that
![]() (17)
(17)
Finally, we recall that
![]() (18)
(18)
![]() (19)
(19)
3.2. Computation of the Action of the Generalized Field Operator on the Basis (Fn)n
In the remain, we take ![]() and we assume that second order moment of
and we assume that second order moment of ![]() is finite. Let
is finite. Let ![]() be the function given by
be the function given by![]() , where
, where
![]()
Since the set ![]() is total in
is total in ![]() (See (11)), then
(See (11)), then ![]() is also total. Then by the Gram-Schmidt procedure, we construct an Hilbertian basis of it, that is denoted by
is also total. Then by the Gram-Schmidt procedure, we construct an Hilbertian basis of it, that is denoted by
![]() (20)
(20)
Lemma 3.1. If the 4th-moment of ![]() is finite then
is finite then ![]() for all
for all![]() .
.
Proof. We have
![]()
Then![]() . Since
. Since ![]() for all
for all![]() , then it is sufficient to prove that
, then it is sufficient to prove that![]() .
.
We have
![]()
where we have used the condition (10).
![]()
,
Proposition 3.1. Let ![]() be the orthogonal basis of
be the orthogonal basis of ![]() given by
given by
![]()
where ![]() is the basis given by (20). Then we have
is the basis given by (20). Then we have
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
where![]() .
.
Remark 1. Note that the relation (22) still true in the case when ![]() with convention that
with convention that![]() .
.
Proof. From (5), we have
![]()
![]()
This prove (21).
From (5), we have
![]() (24)
(24)
Here, we have two cases:
If![]() , then (24), becomes
, then (24), becomes
![]() (25)
(25)
If![]() , then
, then ![]() for all
for all![]() . Therefore (24) gives
. Therefore (24) gives
![]()
But in view of (17), we have ![]() which gives that the relation (25) sill true. Hence (22) is proved.
which gives that the relation (25) sill true. Hence (22) is proved.
Now, it remains to justify (23). From (7), we get
![]() (26)
(26)
Since![]() , then it can be written as follows:
, then it can be written as follows:
![]()
Using the fact that ![]() is bounded, the Equation (26) becomes
is bounded, the Equation (26) becomes
![]() (27)
(27)
But we have for![]() ,
,
![]() (28)
(28)
Then (27) becomes
![]()
This ends the proof. ,
Corollary 3.1.1 The action of the generalized field operator Q on the basis ![]() is given as follows:
is given as follows:
![]()
(29)
Proof. A straightforward computations. ,
4. Orthogonal Functions and Generalization of the Three-Term Recurrence Relation
In this section, we give the action of the multiplication operator q on the functions
![]()
Then we deduce the generalization of the three-term recurrence relation in term of the orthogonal functions![]() .
.
Since U is unitary from ![]() to
to ![]() and
and ![]() is an orthogonal basis of
is an orthogonal basis of![]() , the family
, the family ![]() is an orthogonal basis of
is an orthogonal basis of![]() .
.
Theorem 4.1 Let ![]() and let
and let ![]() be the diagonal operator from
be the diagonal operator from ![]() to itself given by
to itself given by
![]()
Then for all![]() , we have
, we have
![]() (30)
(30)
Remark 2. Since U is unitary and the basis ![]() is orthogonal, then
is orthogonal, then ![]() is an orthogonal basis of
is an orthogonal basis of![]() . Moreover, the chaos decomposition of the Fock space
. Moreover, the chaos decomposition of the Fock space ![]() induces the following chaos-decomposition of the space
induces the following chaos-decomposition of the space ![]()
![]()
Now comparing the relation (30) with (3), the only difference is the apparition of a corrective expression ![]() in (30) which is in the nth chaos. In the case when it is null, (30) will be exactly the well-known tri-diagonal recurrence relation (3). In this sense the relation (30) can be interpreted as a generalization of the three term recurrence relation. Here, the monic orthogonal polynomial sequence is replaced by a double-entries sequence of orthogonal functions parameterized by
in (30) which is in the nth chaos. In the case when it is null, (30) will be exactly the well-known tri-diagonal recurrence relation (3). In this sense the relation (30) can be interpreted as a generalization of the three term recurrence relation. Here, the monic orthogonal polynomial sequence is replaced by a double-entries sequence of orthogonal functions parameterized by ![]() and
and![]() . In addition to the infinite divisibility property, this generalization require only the existence of the second and fourth order moments of
. In addition to the infinite divisibility property, this generalization require only the existence of the second and fourth order moments of![]() .
.
Proof. From relation (29), we deduce that
![]()
![]()
Proposition 4.2. We assume that ![]() is continuous w.r.t the Lebesgue measure with Radon-Nikodym derivative
is continuous w.r.t the Lebesgue measure with Radon-Nikodym derivative![]() . Then for all
. Then for all ![]() and
and![]() , one has
, one has
![]() (31)
(31)
where,
![]()
Proof. Since ![]() is an Hilbertian basis of
is an Hilbertian basis of ![]() and
and![]() ,
,
![]()
where the series converge in![]() . It follows, from the multinomial Newton formula (14), that
. It follows, from the multinomial Newton formula (14), that
![]()
where
![]()
This implies that
![]()
From the definition of U, we get
![]()
which is the decomposition of ![]() in the basis
in the basis![]() . Then
. Then
![]()
On the other hand, we have
![]()
This implies that
![]()
or equivalently
![]()
where ![]() denotes the Fourier transform on
denotes the Fourier transform on![]() . Note that the function
. Note that the function ![]() belongs to the space
belongs to the space![]() . It follows that
. It follows that
![]()
,
which is equivalent to
![]()
5. Conclusion
The infinite-divisibility of the distribution ![]() gives rise to the Kolmogorov isomorphism U, which was the principal bridge between the Fock space
gives rise to the Kolmogorov isomorphism U, which was the principal bridge between the Fock space ![]() and
and ![]() transforming, in such canonical way, the quantum decomposition identity to the tri-diagonal recurrence relation.
transforming, in such canonical way, the quantum decomposition identity to the tri-diagonal recurrence relation.
Acknowledgements
The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, on the material support for this research under the number 3378 during the academic year 1436 AH/2015 AD.