1. Introduction
Alternative explanations to Doppler effect, or expansion of the universe, for observed redshift of luminous objects in distant galaxies, such as tired light models, have never been taken seriously since it was first offered by Zwicky in 1929 [1] . There are many studies that show that expanding universe approach has certain problems, such as requiring simplifying assumptions and multiple parameters to get acceptable fit to the observed data. Geller and Peebles [2] have studied the tired-light static universe concept against the expanding universe concept. LaViolette [3] has shown that the tired-light model provides a better fit to the observed data without requiring the ad hoc introduction of assumptions about rapid galaxy evolution. Ghosh [4] has introduced a velocity dependent ‘inertial induction’ model as a possible mechanism for explaining the redshift in a quasi-static infinite universe. More recently, Marosi [5] , Traunmuller [6] , Orlov and Raikov [7] , and others have shown that the static or slowly expanding universe models are viable alternatives to the standard ΛCDM models. López-Corredoira [8] in his most recent publication has critically analysed static and expansion models and established that both the approaches have unexplained gaps and arbitrariness.
The mechanism that leads to the loss of energy in tired light models has not been made clear in most of the studies although Compton scattering, or like models, have been cursorily suggested. The most used form of the tired light approach takes an exponential increase in photon wavelength with distance traveled:
, (1)
where
is the observed wavelength of the photon at distance d from the source of emission,
is the wavelength of the photon at the source of light and
is a constant that characterises the effect of the cause of the increase in wavelength whatever that may be.
The focus here is to derive Equation (1) from a simple model of resistance of the fields in space to the propagation of photons (and possibly other particles), similar to that of the propagation of a particle through a resistive field of a fluid in fluid dynamics
2. Cosmic Drag Model
In fluid dynamics, the particle ceases to accelerate when the applied force on a particle F equals fluid’s resistance or drag:
. (2)
Here
is the density of the fluid through which the particle is propagating, v is the particle velocity, A is the particle area and
is the fluids drag coefficient. Now this force F may also be written as
where dE is the energy used up in moving the particle a distance dx in the fluid.
. (3)
Inspired by this equation, in our phenomenological cosmic drag model for a photon traveling through space, we write as follows:
, with h as Planck’s constant and
as photon frequency,
is assumed to be proportional to the energy E,
is a constant related to the entity causing the drag,
, the speed of light.
We may then write:
. (4)
Here
is a constant that captures
and the proportionality constant that relates E to
, thus representing the resistive properties of the cosmic drag fields on the photon. Integrating Equation (4) over distance d from the photon emission point to the photon observation point, we have:
, (5)
or
, (6)
or
. (7)
Here,
and
are respectively the emitted and observed photon frequencies and
. Now, since the redshift is defined as
, we may write Equation (7):
, (8)
or
(9)
The constant
can be determined from the small redshift limit of Equation (9) by appealing to the Hubble law. The law may be written for small z as
, where
is Hubble constant and d is the distance of a galaxy with small redshift. This allows us to write for small values of z
, (10)
or
, and (11)
. (12)
Taking
and
(= 70 km/s/Mpc), we get
. Before we proceed further let us see if this constant has some cosmological meaning.
3. Mass of the Universe
Looking at Newton’s gravitational constant
, we notice that its dimensions are m3×k−1×s−2 with a value of 6.674 × 10−11. Thus on the dimensional ground,
, (13)
where
is an unknown mass factor related to the propagation of light in the universe. This yields
. (14)
We can readily recognize this as the mass of the observable universe (Hoyle-Carvalho formula [9] ); it is in the same range as estimated in several studies, e.g. Valev [10] and Ostriker et al. [11] .
Substituting
from Equation (13) into Equation (4), we have,
. (15)
This equation shows that the drag on the photon depends on the mass of the observable universe and thus it is a manifestation of Mach’s Principle [12] . We may therefore call this redshift as due to Mach Effect.
4. Observed Data Analysis
We will now proceed to fit the observed redshift data using the Doppler effect (including expansion effect) based model and the Mach effect based model proposed here, to explore if one or the other gives a better fit, or perhaps both the effects are partially accountable for the observed redshift. The model we chose for the first type is that recently developed analytically by Mostaghel [13] assuming a flat universe expanding under a constant pressure and combining the first and second Friedmann equations. This model yields a good fit to the whole range of redshift that was available to him in late 2015 as follows:
1) A set of 557 SNe data with redshifts from
as compiled in the 2010 in the Union2 database [14] ;
2) A set of 394 extragalactic distances to 349 galaxies at redshifts
as reported in 2008 NASA/IPAC’s NED-4D database [15] ; and
3) Data for three most distant recently confirmed galaxies [16] [17] [18] , and a quasar [19] with
.
The distance modulus
and the redshift z are represented by Mostaghel [13] as
(16)
where a is the scale factor,
is in mega parsecs, and
includes K-correction that corrects observation data for source luminosity, instrumental factors, and other factors. With
and
,
. (17)
Mostaghel fitted 1st set of data in Equation (17), and found
. This equation was used to fit all the three sets of data showing a reasonably good fit. (It should be mentioned that we found for all the three data sets a better fit is obtained by using
and not by using
). He used his analytically derived value of
km/s/Mpc in Equation (17) as he found it to be very close to the average of the most recently reported value of the Hubble constant. He found
plots using Equation (17) were in good agreement with
CDM model fit with the same data using the scale factor given by equation
, (18)
with
,
,
,
and
. We there for used Equation (18) as representing the expansion model, i.e. the Doppler effect model.
Based on Equation (12) for Mach effect model, distance modulus may be written as
, (19)
with
is correction factor for Mach Effect and d is determined by fitting the observational data.
The observational data we chose for our study is only slightly different from Mostaghel’s data discussed above. We took (a) a set of 580 SNe data with redshifts from
as compiled in the 2010 in the Union2 database [14] ; and (b) a set of 382 extragalactic redshifts
as reported in the updated 2017 NASA/IPAC’s NED-D database [15] . The plots fitted to determine b and d using non-linear regression analysis, presented in Figure 1 show the fit of the two models with the low z observed data set (a). Figure 2 plots include both the data sets (a) and (b) for the fit. The first four rows of Table 1 presents the values of b and d for both the cases along with their 95% confidence bounds, SSEs (sum of squares due to errors), R-squares, and RMSE (root mean square errors).
As the redshift may be partly due to Doppler effect and partly due to Mach effect, we also considered fitting the observed data with weight factors given to Equations (17) and (19) and determining the weight factors with nonlinear regression analysis. Thus, we may write
, (20)
where w is the weight factor given to Equation (19) and
to Equation (17); two weight factors must add up to 1 and
. Parameters b and d we tried in Equation (20) for determining w are as follows: 1) determined from fitting data set (a), that is
and
; 2) determined from fitting the combined dataset (a) and (b), that is
and
; and 3)
![]()
Figure 1. Observed data set
fitted using Doppler Effect and Mach Effect based models.
![]()
Figure 2. Observed data set
fitted using Doppler Effect and Mach Effect based models.
and
. While parameters b and d may also be determined along with
by fitting Equation (20) directly to the observed data, their variance becomes very high due to significant scatter in observed data. The fitted curves for the three cases are plotted in Figure 3 and corresponding weight factors w along with their associated analysis parameters are given in Table 1 in the last three rows.
![]()
Figure 3. Observed data set
fitted using a hybrid Doppler Effect and Mach Effect model with the weight factor for the two determined for the three cases: 1)
and
; 2)
and
; and 3)
and
.
![]()
Table 1. Parameters obtained by fitting observed 2010 Union2 [14] and 2017 NASA/IPAC’s NED-D database [15] to different models.
The weight factor appears to strongly favour Mach effect;
. However due to logarithmic dependence of
on z, w is also strongly dependent on parameters b and d of the
and
factors, which in turn heavily depends on the K-correction. Here we are assuming that both the effects determine
and z. Then, if we use the equation that only represent one effect, the exponent of
, with
or d, has to take care of not only the K-correction, etc., but also for the other effect. Since d comes out to be up to 20% greater than 1, while b comes out to be up to 25% less than 2 (first four rows of Table 1), when using respective single effect equations, we believe taking
and
for the first term and the second term respectively in Equation (20) may not be unreasonable to fit the data to determine w. This is why we have included case (3) for Figure 3 and Table 1 (last 3 rows). As can be seen case (3) gives almost identical result to case (2), which is better than case (1). We therefore decided to pursue further the case
and
by rewriting Equation (20) as follows:
, (21)
where
is now the Doppler effect weight factor. Sixteen data sets were created with progressively increasing value of
; say for
all the data up to
was included. For each data set,
was determined by fitting the data using Equation (21). Resulting 16 data points
were then fitted using a Gaussian function with the constraint that the factor
satisfy the condition
. The plot is shown in Figure 4. We see a peak at
with
and FWHM of 3.38.
One problem with this plot we noticed is that the constraint
was hit 8 times. This suggests that
has a tendency to go negative. When we removed the constraint on
, we got the data points that fitted beautifully a two term sine function (Figure 5):
, (22)
with
,
,
;
,
,
. This amounts to the Doppler effect contribution in Equation (21) to be negative in some regions and positive in others.
We may interpret the positive
as indicative of the expansion of the universe and negative
as contraction. As per Figure 5, the expansion of the universe starts at
, peaks at
, slows down up to
, and then goes into contraction phase. The contraction peaks at
, slows down up to
, and then goes into expansion phase again; and so on. This fit may be extrapolated to higher values of μ using Equation (22) well beyond the maximum μ shown in the figure. This is shown in Figure 6 from
![]()
Figure 4. The Doppler effect weight factor
bound to the condition
and calculated using progressively incremental observed data base at 16 μ points shows a Gaussian behaviour. A peak is seen at
with
and FWHM of 3.38.
![]()
Figure 5. The Doppler effect weight factor
liberated from the condition
and calculated using progressively incremental observed data base at 15 μ points shows a good fit to a two term sine function
.
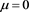 to
to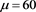 ―the universe is expanding in some regions and contracting in others [20] .
―the universe is expanding in some regions and contracting in others [20] .
It should be mentioned that the parameter b and d in  and
and 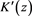 respectively, when determined by fitting progressively incremental observed data, show oscillatory behaviour at their respective average value similar to
respectively, when determined by fitting progressively incremental observed data, show oscillatory behaviour at their respective average value similar to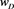 . This may be interpreted as if
. This may be interpreted as if 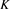 and
and 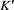 factors are varying with
factors are varying with ![]() to effectively correct for the missing effect in their respective Equations (17) and (19). However, they lack any explanation for such behaviour. It remains to be seen if the phenomenological model proposed here can be derived in a fundamental manner.
to effectively correct for the missing effect in their respective Equations (17) and (19). However, they lack any explanation for such behaviour. It remains to be seen if the phenomenological model proposed here can be derived in a fundamental manner.
5. Conclusion
The extragalactic redshift has been shown to be due partly to the Doppler effect (expansion of the universe) and partly due to Mach effect by analysing up to date data available from Union2 and NASA/NED data bases. The model resulting in Mach effect yields mass of the observable universe as![]() . The weight factor determining the two contributions shows an oscillatory behavior against distance modulus when progressively larger set of the database is fitted using the hybrid model comprising both the Doppler effect and the Mach effect. It suggests that the universe is expanding at some radial distances from the observer and contracting at others. However, the phenomenological model for the Mach effect proposed here needs to be related to fundamentals cosmology.
. The weight factor determining the two contributions shows an oscillatory behavior against distance modulus when progressively larger set of the database is fitted using the hybrid model comprising both the Doppler effect and the Mach effect. It suggests that the universe is expanding at some radial distances from the observer and contracting at others. However, the phenomenological model for the Mach effect proposed here needs to be related to fundamentals cosmology.
Acknowledgements
We wish to thank Professor Naser Mostaghel for providing the SNe and Union2 observational data used in his research paper [13] , and Professor López-Corredoira for his critical comments on this paper and for providing a copy of his most recent review paper [8] . Acknowledgement is also due to Professor James Peebles who has suggested that the new approach should also be considered for explaining the observed Microwave Background Radiation profile.