Discussion on the Energy Parallax and the Relationship to Perturbation Theory in Mathematical Physics ()
1. Introduction
1.1. Work Overview
Perturbation theory has played an important role in the development of mathematics and physics from the end of the 19th century. With the pioneering work of H. Poincaré in the theory of dynamical systems, the perturbation theory found a major application in the emergence of quantum mechanics with the preliminary works of M. Bore and W. Heisenberg [4] .
In quantum mechanics, perturbation theory generates states of a system that are adiabatically or linearly derived from a stable state. This stable state is generally an exact solution of the equations describing the system at hand. However, the system can be perturbed in a way that the exact solution, associated with the stable state, is no longer valid to model the changes in the system. Perturbation theory has been formulated in various domains, beyond quantum mechanics, using small quantities in order to describe the perturbed states, degenerated from the stable state. This perturbation shows up as a broadening of the initial energy quantity corresponding to the system in stable state [4] [5] .
In previous works (i.e., [1] [2] [6] [7] ), we define the Energy Spaces, which are subspaces of the Schwartz Space 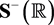 [8] associated with energy operators and generalized energy operators. This definition was used to define the concept of multiplicity of the solutions in [1] (Theorem 2 and Corollary 1). The idea is to consider those energy spaces and functions associated with them when solving linear Partial Differential Equations (PDEs). More precisely, we look for solutions of a nominated linear PDE within those energy spaces. The concept was further developed using the Taylor series of the energy of a solution
[8] associated with energy operators and generalized energy operators. This definition was used to define the concept of multiplicity of the solutions in [1] (Theorem 2 and Corollary 1). The idea is to consider those energy spaces and functions associated with them when solving linear Partial Differential Equations (PDEs). More precisely, we look for solutions of a nominated linear PDE within those energy spaces. The concept was further developed using the Taylor series of the energy of a solution  for a nominated PDE. The work was based on finding when the successive derivatives, defined through the Taylor series coefficients, are also solutions of this particular PDE (see Section 4 in [1] ). The work was then generalized, considering
for a nominated PDE. The work was based on finding when the successive derivatives, defined through the Taylor series coefficients, are also solutions of this particular PDE (see Section 4 in [1] ). The work was then generalized, considering 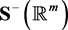 (m in
(m in ,
,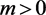 ) [2] using the properties for the Sobolev spaces, the Schwartz space and the L2-norm. The concept of energy parallax was also introduced based on Theorem 3.
) [2] using the properties for the Sobolev spaces, the Schwartz space and the L2-norm. The concept of energy parallax was also introduced based on Theorem 3.
This work is a discussion between the energy parallax and the perturbation theory developed in quantum mechanics. In the next section, we recall this theory. An overview of the energy parallax together with the formal theory developed in [2] using the properties of the Schwartz space 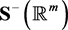 and the L2 space, is briefly exposed at the beginning of Section 3. Through several examples, we discuss the similarities between the two theories. Finally, Section 5 is a discussion on the application of the energy parallax in the derivation of the Woodward effect for the special case of the asymmetric cavities. A conclusion ends this work.
and the L2 space, is briefly exposed at the beginning of Section 3. Through several examples, we discuss the similarities between the two theories. Finally, Section 5 is a discussion on the application of the energy parallax in the derivation of the Woodward effect for the special case of the asymmetric cavities. A conclusion ends this work.
1.2. Notation and Symbols
In this work, several symbols are used. The set of integer numbers 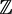 is sometimes called only for the positive integer such as
is sometimes called only for the positive integer such as 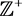 or
or 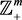 (for a space with dimension m). When the integer 0 is not included, it is explicitly mentioned such as
(for a space with dimension m). When the integer 0 is not included, it is explicitly mentioned such as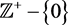 . The set of natural numbers is
. The set of natural numbers is , with only the positive numbers defined as
, with only the positive numbers defined as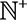 .
. 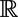 is the set of real numbers. Also, in this paper, the Schwartz space is called
is the set of real numbers. Also, in this paper, the Schwartz space is called 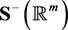 which is the notation used in previous works such as [1] and [2] . Several notations describe the relationship between spaces such as intersection (
which is the notation used in previous works such as [1] and [2] . Several notations describe the relationship between spaces such as intersection ( ), union (
), union ( ), inclusion (
), inclusion ( , inclusion without the equality
, inclusion without the equality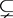 , inclusion with equality
, inclusion with equality![]() ). Readers can refer to [9] or advanced mathematical textbooks for more explanations.
). Readers can refer to [9] or advanced mathematical textbooks for more explanations.
2. An Overview of Perturbation Theory and the Application in Quantum Mechanics
Following [4] , we can consider a simple problem with, let us say, a natural system![]() , initial state
, initial state ![]() and small perturbation
and small perturbation![]() , such as
, such as![]() . Knowing that the system can evolve (or be perturbed) with incremental quantities, the general idea is to model these different states of the system. For example, we can model the next state as
. Knowing that the system can evolve (or be perturbed) with incremental quantities, the general idea is to model these different states of the system. For example, we can model the next state as ![]() with some assumptions such as
with some assumptions such as ![]() (i.e.
(i.e.![]() ). We can then model the i-th phase of the system with the perturbation
). We can then model the i-th phase of the system with the perturbation![]() . Note that the perturbation theory can be applied to the variations of the system’s energy or solutions describing the system’s evolution.
. Note that the perturbation theory can be applied to the variations of the system’s energy or solutions describing the system’s evolution.
However, perturbation theory can only estimate solution close to the exact solution. The addition of the small quantities to the exact solution can be expressed in (power) series (i.e. Taylor series around a nominated quantity―time, position in space, ... ). If the quantity becomes large, the series can diverge and the resulting solution is not valid to describe the perturbed system. In the example of our simple system described above, we have the condition that it exists N in ![]() such as
such as![]() . The various perturbations of the system can then be written such as
. The various perturbations of the system can then be written such as![]() . In other words, the perturbation theory applied to our simple system is expressed through the series
. In other words, the perturbation theory applied to our simple system is expressed through the series![]() . This series may converge or not. The convergence/divergence properties in the perturbation theory is an important research topic [10] [11] [12] . Note that the intermediate states of the system are called degenerated states.
. This series may converge or not. The convergence/divergence properties in the perturbation theory is an important research topic [10] [11] [12] . Note that the intermediate states of the system are called degenerated states.
In quantum mechanics, those states are associated with intermediate levels of energy. These intermediate states are also solving the equations describing the system [5] [13] . For example, let us recall the Rayleigh-Schrödinger perturbation theory. The system is described by the Hamiltonian operator (H) and the solutions describing the different states of the system are the eigenfunctions (![]() ) of H. In fact, we have the famous relationship between the Hamiltonian, the eigenfunctions and the corresponding energy states (
) of H. In fact, we have the famous relationship between the Hamiltonian, the eigenfunctions and the corresponding energy states (![]() ),
),![]() [13] . Thus, the perturbation in the system is described with a term V such as the Hamiltonian is also changed with
[13] . Thus, the perturbation in the system is described with a term V such as the Hamiltonian is also changed with![]() .
. ![]() is the small quantity varying in
is the small quantity varying in![]() . The power series of the eigenfunction at the n-th order
. The power series of the eigenfunction at the n-th order
perturbation can be written such as ![]() and the associated energy
and the associated energy![]() . The formula of
. The formula of ![]() and
and ![]() are called the Lindset series for a
are called the Lindset series for a
Hamiltonian operator driven by small perturbations [14] . Thus, there is a linear relationship between the degenerate states ![]() and the associated small energy quantity
and the associated small energy quantity![]() . Finally, the energy quantities and the associated eigenstates can be directly related to the total energy of the system
. Finally, the energy quantities and the associated eigenstates can be directly related to the total energy of the system ![]() and its associated eigenfunction
and its associated eigenfunction ![]() such as [13] :
such as [13] :
![]() (1)
(1)
It is important to recall for the following that the perturbations for integrable Hamiltonian system are described by the Kolmogorov-Arnold-Moser (KAM) theorem [14] . The KAM theorem deals with persistence, under perturbation, of quasi-periodic motions in Hamiltonian dynamical systems.
3. Energy Parallax and relationship with Perturbation Theory
This section starts with a short summary of the energy space theory, which defines the energy parallax. Readers can refer to [1] [2] [6] for a comprehensive description of the work. The second part discusses about the common features with the perturbation theory through some examples.
3.1. Short Review of the Energy Parallax
The concept of multiplicity of the solutions was developed in [1] which is based on the theory of energy operators in the Schwartz space ![]() and some subspaces called energy spaces first defined in [7] and subsequently in [1] . The main idea is to look for solutions of a given linear PDE in those subspaces. The theory has been recently extended (e.g., [2] ) in
and some subspaces called energy spaces first defined in [7] and subsequently in [1] . The main idea is to look for solutions of a given linear PDE in those subspaces. The theory has been recently extended (e.g., [2] ) in ![]() (
(![]() ) using the theory of Sobolev spaces, and in a special case the Hilbert spaces. In [2] , the author uses the Sobolev embedding theorem in order to show the Theorem 3 and the concept of multiplicity of the solutions.
) using the theory of Sobolev spaces, and in a special case the Hilbert spaces. In [2] , the author uses the Sobolev embedding theorem in order to show the Theorem 3 and the concept of multiplicity of the solutions.
Furthermore, the author defines in [1] the concept of energy parallax, in order to understand the physical meaning of including additional solutions when varying the energy of a predefined system locally by taking into account additional smaller quantities. It is equivalent to take into account solutions in other energy subspaces (e.g., Theorem 3, [2] ).
To recall [1] [2] [7] , a possible application of the theory of the energy operators is to look at solutions of a given partial differential equation for solutions in ![]() of the form
of the form![]() . Instead of solving the equation for specific values (e.g., boundary conditions), the work in [1] (e.g., Theorem 2 and corollary) defines the concept of multiplicity of the solutions in
. Instead of solving the equation for specific values (e.g., boundary conditions), the work in [1] (e.g., Theorem 2 and corollary) defines the concept of multiplicity of the solutions in ![]() (
(![]() ) such as the study of the multiple solutions of a PDE based on the definition of the energy spaces
) such as the study of the multiple solutions of a PDE based on the definition of the energy spaces ![]() (
(![]() ). One way to understand this concept, is to study the convergence of the development in Taylor series of the energy function associated with a nominated energy space. It was shown in [7] that taking into account additional terms of the Taylor series leads to define additional solutions of the wave equation (see Section 4 [1] ). It was further generalized in [2] (Section 5) with
). One way to understand this concept, is to study the convergence of the development in Taylor series of the energy function associated with a nominated energy space. It was shown in [7] that taking into account additional terms of the Taylor series leads to define additional solutions of the wave equation (see Section 4 [1] ). It was further generalized in [2] (Section 5) with ![]() (
(![]() ) and the solutions in the subspaces
) and the solutions in the subspaces ![]() (
(![]() ,
,![]() ). Note that the inclusion of the energy subspaces is shown in [2] using the properties of the Sobolev spaces. The energy spaces
). Note that the inclusion of the energy subspaces is shown in [2] using the properties of the Sobolev spaces. The energy spaces ![]() are defined following [2] (Definition 3).
are defined following [2] (Definition 3).
Definition 1. [2] : The energy space![]() , with p in
, with p in![]() , is equal to
, is equal to![]() . with
. with ![]() for v in
for v in ![]() defined as
defined as
![]() (2)
(2)
![]() is a generalized energy operator defined in [2] . In order to understand the notation,
is a generalized energy operator defined in [2] . In order to understand the notation, ![]() ,
, ![]() and
and![]() . Now, let us define any PDEs of the form:
. Now, let us define any PDEs of the form:
![]() (3)
(3)
Thus, all the solutions are here defined in![]() . Now, we are interested in the solutions which can be defined on the energy spaces
. Now, we are interested in the solutions which can be defined on the energy spaces ![]() (
(![]() ). In other words,
). In other words,![]() . In particular, we choose the solution
. In particular, we choose the solution![]() . Furthermore, one can define
. Furthermore, one can define ![]() , such as
, such as ![]() for
for![]() . In other words,
. In other words, ![]() and
and![]() , such as
, such as![]() .
.
The theorem of (Multiplicity of Solutions in![]() ) stated in [2] (Theorem 3) is:
) stated in [2] (Theorem 3) is:
Theorem 1. If ![]() is a subspace of all the solutions of a nominated linear PDE. For
is a subspace of all the solutions of a nominated linear PDE. For![]() , g is in
, g is in![]() . Then, g is a solution for this linear PDE if and only if:
. Then, g is a solution for this linear PDE if and only if:
1) (General condition to be a solution)![]() .
.
2) (Solutions in![]() )
)![]() ,
, ![]() such as
such as ![]() .
.
3) (Multiplicity of the solutions) If ![]() (
(![]() ),
),![]() and
and![]() , such as
, such as ![]() (
(![]() ) and
) and![]() ,
, ![]() ,
,![]() .
.
4) (Superposition of solutions and energy conservation ) If![]() , with
, with ![]() such as
such as ![]() (
(![]() ), then
), then![]() .
.
Readers can refer to the appendices in [2] for further information on the energy space theory. Note that, in [1] , the theorem on the multiplicity of the solutions was established for the function of finite energy in ![]() (m in
(m in![]() ). [2] generalizes the same theorem for m in
). [2] generalizes the same theorem for m in ![]() (
(![]() ), thanks to the theory of Sobolev Spaces.
), thanks to the theory of Sobolev Spaces.
Furthermore, let us recall a proposition first stated in [1] (i equal 1) and generalized (![]() )) in [2] .
)) in [2] .
Proposition 1. If for![]() ,
, ![]() and analytic; for any
and analytic; for any ![]() and
and ![]() (
(![]() ), and
), and ![]() is analytic, where
is analytic, where
![]() (4)
(4)
then
![]() (5)
(5)
is a convergent series.
3.2. Examples and Discussion between the Energy Parallax and the Perturbation Theory
In areas where the solutions are described via a set of PDEs, the perturbation theory can be rather complicated to use. Instead, the energy parallax shows that the variations of energy quantity lead to define solutions according to the spaces associated with the energy quantities (or energy spaces as defined in Definition 1). Theorem 1―the multiplicity of the solutions―lays the basis to define the solutions associated with the perturbed system, every time the energy increases in small quantities. Let us recall the definition of energy parallax [2] (Definition 4):
Definition 2. Considering a linear PDE with some solutions in ![]() such as
such as![]() . Furthermore, if it exists p and
. Furthermore, if it exists p and ![]() such as
such as![]() , then we associate the energy
, then we associate the energy ![]() for
for ![]() , such as one can estimate the variation
, such as one can estimate the variation ![]() over an elementary quantity
over an elementary quantity ![]() (e.g., space, time or space-time for the specific case m in
(e.g., space, time or space-time for the specific case m in![]() ). If
). If ![]() is not negligible (
is not negligible (![]() such as
such as ![]() and
and![]() ), then one can consider additional solutions in
), then one can consider additional solutions in![]() .
.
The validity of this approach is only guaranteed if the power series of the energy is converging. The convergence properties is essential, because of the assumptions of small variations of energy. Due to those small energy variations, a limited number of energy subspaces are taken into account and thus a limited number of additional solutions are introduced in the considered system. This idea is written mathematically in the superposition of solutions and energy conservation, property 4 in Theorem 1. That is why the fundamental work in [6] [7] focuses on the function of finite energy in the Schwartz space ![]() (m in
(m in![]() ) in [2] .
) in [2] . ![]() is the L2 space associated with the 2-norm on
is the L2 space associated with the 2-norm on![]() .
.
To illustrate the energy parallax, let us come back to our simple system example used in the explaination of the perturbation theory. The energy of this system ![]() increases slowly such as
increases slowly such as![]() . If we assume that the space of
. If we assume that the space of
the solutions of PDEs describing this system is![]() . We can then assume that if
. We can then assume that if![]() , the power series
, the power series
![]() is convergent.
is convergent. ![]() depends on the variables of
depends on the variables of![]() . In the classical formulation of a Taylor series with a function depending on time,
. In the classical formulation of a Taylor series with a function depending on time, ![]() and
and ![]() is some initial time/coordinate where the development is realized.
is some initial time/coordinate where the development is realized.
Let us consider that ![]() is equal to
is equal to![]() . Now, applying Proposition 1, the power series
. Now, applying Proposition 1, the power series ![]() is convergent. Knowing that
is convergent. Knowing that ![]() (
(![]() ) (i.e. Proposition 1 ), the definition of the energy space recalls that the solutions
) (i.e. Proposition 1 ), the definition of the energy space recalls that the solutions![]() . The energy parallax with Theorem 1 states the conditions when the solutions of the form
. The energy parallax with Theorem 1 states the conditions when the solutions of the form ![]() (
(![]() ) are also solutions in
) are also solutions in ![]() (or
(or![]() ). The general idea is that when the energy of the system increases of a small quantity (i.e.
). The general idea is that when the energy of the system increases of a small quantity (i.e.![]() ), one can look at solutions with higher derivatives (i.e.
), one can look at solutions with higher derivatives (i.e.![]() ) belonging to
) belonging to![]() .
.
Let remind us of an example in functional analysis first shown in [7] in order to illustrate the energy parallax.
3.2.1. Example 1: Specific Solutions of the Wave equation in ![]()
As a simple case of linear PDE, the wave equation with the particular solutions of the form of evanescent waves, was already discussed in Section 6 of [7] and [2] . However, it is an interesting example to apply and understand the concept of multiplicity of the solutions stated in [2] (e.g., Theorem 3) and recall in Theorem 1. From [15] , the wave equation can be formulated in ![]() (with t and r the time and space variables):
(with t and r the time and space variables):
![]() (6)
(6)
c is the speed of light. Note that the values of t and r are restricted to some interval, because it is conventional to solve the equation for a restricted time interval in ![]() and a specific region in space. According to the previous section, here we are interested in the solutions in the energy (sub)space
and a specific region in space. According to the previous section, here we are interested in the solutions in the energy (sub)space![]() , of the kind
, of the kind
![]() (n in
(n in![]() , p in
, p in![]() , k in
, k in![]() ). Furthermore, the relationship
). Furthermore, the relationship ![]() imposes that the solutions should be
imposes that the solutions should be
finite energy functions, decaying for large values of r and t. It was previously underlined in [1] [2] that planar waves should be rejected, because this type of
solution does not belong to![]() . However, evanescent waves are a type of solutions included in
. However, evanescent waves are a type of solutions included in ![]() and considered in this work. They are here defined such as:
and considered in this work. They are here defined such as:
![]() (7)
(7)
![]() ,
, ![]() and
and ![]() are the wave numbers,
are the wave numbers, ![]() is the angular frequency and A is the amplitude of this wave [15] . Assuming
is the angular frequency and A is the amplitude of this wave [15] . Assuming ![]() and (
and (![]() ,
,![]() ) known, one can add some boundary conditions in order to estimate
) known, one can add some boundary conditions in order to estimate![]() ,
, ![]() and A. Furthermore, a traveling wave solution of (6) should satisfy the dispersion relationship between
and A. Furthermore, a traveling wave solution of (6) should satisfy the dispersion relationship between![]() ,
, ![]() and
and ![]() [15] . However, our interest is just the general form assuming that all the parameters are known. For
[15] . However, our interest is just the general form assuming that all the parameters are known. For![]() , the type of solutions in
, the type of solutions in ![]() are:
are:
![]() (8)
(8)
In![]() , one can then write the type of solutions
, one can then write the type of solutions
![]() (9)
(9)
Let us consider the form of solutions which propagates in a closed cavity (e.g., closed wave guide [15] ). One possible solution is the evanescent wave described in (7). Now, if f and ![]() are analytic in
are analytic in![]() , it was shown (see Proposition 1 in [2] and Proposition 1) that f is finite energy (and more generally in
, it was shown (see Proposition 1 in [2] and Proposition 1) that f is finite energy (and more generally in![]() ) with a wise choice on the parameters A,
) with a wise choice on the parameters A, ![]() ,
, ![]() and
and![]() . One can estimate the difference of energy in time over
. One can estimate the difference of energy in time over ![]() inside the cavity at a specific location
inside the cavity at a specific location ![]() (
(![]() in
in![]() ) such as
) such as
![]() (10)
(10)
Here the symbol “![]() ” means that
” means that
![]() (11)
(11)
Now, let us do a hypothesis that ![]() increases significantly over
increases significantly over ![]() modifying the approximation in (11)
modifying the approximation in (11)
![]() (12)
(12)
and then,
![]() (13)
(13)
To recall that![]() ,
, ![]() and
and![]() , and using Theorem 1, one can take into account solutions in those (energy) subspaces. The multiplicity of the solutions (i.e., Theorem 1), due to the variation of energy, can be formulated as an approximation for taking into account additional solutions produced by the wave equation.
, and using Theorem 1, one can take into account solutions in those (energy) subspaces. The multiplicity of the solutions (i.e., Theorem 1), due to the variation of energy, can be formulated as an approximation for taking into account additional solutions produced by the wave equation.
Discussion (1): With the above example, we can now expose some common features between the energy parallax formulation and the perturbation theory. Firstly, one can emphasize the Lindset series of the energy (![]() ) and the eigenfunctions (
) and the eigenfunctions (![]() ) described in Section 2. To recall Section 3.2, the energy parallax theory uses the Taylor Series development of a general solution
) described in Section 2. To recall Section 3.2, the energy parallax theory uses the Taylor Series development of a general solution
![]() for a given PDE (with
for a given PDE (with![]() ) associated with the Taylor Series
) associated with the Taylor Series
of the corresponding energy![]() . In quantum mechanics, perturbation theory relies on the Hermitian properties of the Hamiltonian, which establish the relationship between the energy states and the eigenfunctions. However, the energy parallax theory is not based on an explicit operator, which establishes a direct relationship between the energy increments and the perturbation of the general solution.
. In quantum mechanics, perturbation theory relies on the Hermitian properties of the Hamiltonian, which establish the relationship between the energy states and the eigenfunctions. However, the energy parallax theory is not based on an explicit operator, which establishes a direct relationship between the energy increments and the perturbation of the general solution.
The energy spaces ![]() (p and
(p and![]() ) together with the Theorem 1 describe how the perturbation in the power series of the energy leads to consider additional solutions based on the higher order derivatives of the primary (original) solution. Technically, we showed in [2] the inclusion of the energy (sub)spaces (i.e.,
) together with the Theorem 1 describe how the perturbation in the power series of the energy leads to consider additional solutions based on the higher order derivatives of the primary (original) solution. Technically, we showed in [2] the inclusion of the energy (sub)spaces (i.e., ![]() ,
, ![]() ,
,![]() ) similar to the Sobolev embedding theorem (see [2] , Properties 2). Unlike the perturbation theory where the solutions are expressed in power series with the addition of small quantities to take into account the perturbation of the system’s energy, the energy parallax considers additional solutions to a given PDE (or PDEs describing a given system) based on the higher order derivatives of the primary solution when considering higher order perturbations of the system’s energy.
) similar to the Sobolev embedding theorem (see [2] , Properties 2). Unlike the perturbation theory where the solutions are expressed in power series with the addition of small quantities to take into account the perturbation of the system’s energy, the energy parallax considers additional solutions to a given PDE (or PDEs describing a given system) based on the higher order derivatives of the primary solution when considering higher order perturbations of the system’s energy.
Note that our formulation of the energy parallax is at the moment restricted to functions in![]() , and thus finite energy function. Thus, every function (general solution of the PDE, additional solutions defined on the energy spaces, superposition of all the solutions) should be finite energy function to guarantee that they are in
, and thus finite energy function. Thus, every function (general solution of the PDE, additional solutions defined on the energy spaces, superposition of all the solutions) should be finite energy function to guarantee that they are in ![]() [2] .
[2] .
3.2.2. Example 2: Application to EM Field Theory
Perturbation theory may be difficult to implement when the system is described by a set of PDEs. One area in particular is the area of field theory such as Electro Magnetic (EM) field with EM waves as solutions of those PDEs. The term field is first coined by M. Faraday in 1849. The work of J. C. Maxwell leaded to the discovery of the propagation of EM waves [15] . A turning point is the introduction of the special theory of relativity by. A. Einstein in 1905 with no longer relationship between the speed of the observer and the velocity of the waves. Field theory becomes even more important with the development of quantum mechanics in the late 1920s and the work of P. Dirac using the emerging theory of quantum field theory to explain the energy decay of an atom between different quantum states [16] .
Let us recall an example of variation of EM energy density in the skin layer of a conductor. The theory of energy space is now applied to the possible variations of electromagnetic energy density due to, for example, skin depth effect [15] inside some conductive material. Beyond this application, the interest is to give a physical meaning of taking into account those additional solutions in various energy spaces. Thus, let us formulate the variation in time of energy density (u) at the second order with a Taylor series development such as:
![]() (14)
(14)
o is the Landau notation to omit higher order quantities. Note that at the first order![]() . The higher order terms are based on the assumptions that the
. The higher order terms are based on the assumptions that the
EM waves inside the skin layer of the copper plate are evanescent waves and thus functions in the Schwartz space (![]() ―with 3 dimension variables and considering also the time ) [15] . As discussed before, those solutions are finite energy functions and in
―with 3 dimension variables and considering also the time ) [15] . As discussed before, those solutions are finite energy functions and in ![]() (i.e. following [1] and [7] ,
(i.e. following [1] and [7] , ![]() at some given point in the skin layer defined by the coordinates
at some given point in the skin layer defined by the coordinates![]() ). To recall Section 2, the definition of the energy space
). To recall Section 2, the definition of the energy space![]() , we can state in
, we can state in ![]()
![]() (15)
(15)
Here f is either the electric or magnetic field (i.e. the absolute norm of ![]() and
and ![]() respectively). With the concept of multiplicity of the solutions (e.g., Theorem 1). If g is a general solution of some linear PDEs, then
respectively). With the concept of multiplicity of the solutions (e.g., Theorem 1). If g is a general solution of some linear PDEs, then ![]() can be identified as a special form of the solution (conditionally to its existence ).
can be identified as a special form of the solution (conditionally to its existence ).
Now considering the wave equation, the electric field and magnetic fields are solutions and belong to the subspace ![]() and associated with the variation of energy density
and associated with the variation of energy density![]() . Furthermore, we can consider the solutions in
. Furthermore, we can consider the solutions in ![]() associated with the variation of energy density
associated with the variation of energy density![]() , which can be explained with the concept of multiplicity of the solutions. The solutions of interest in
, which can be explained with the concept of multiplicity of the solutions. The solutions of interest in ![]() are for the electric field
are for the electric field ![]() and the magnetic field
and the magnetic field![]() . The Taylor Series development of the energy of (for example) the electric field on a nominated position in space (i.e.,
. The Taylor Series development of the energy of (for example) the electric field on a nominated position in space (i.e.,![]() ) and in an increment of time
) and in an increment of time![]() :
:
![]() (16)
(16)
Finally one can write the relationship with the energy density following (14) and the previous Taylor series development for the electric and/or magnetic field:
![]() (17)
(17)
Therefore, taking into account the second order term of the energy density ![]() means that additional solutions should also be considered in the EM modeling.
means that additional solutions should also be considered in the EM modeling.
3.2.3. Example 3: Variation of EM Energy density―consequences from thewave theory Point of View
We are taking the example of the variation of EM energy density inside a copper wall due to planar waves reflecting and refracting on it [15] . To recall the previous example, the EM field is now including (![]() ,
,![]() ) and (
) and (![]() ,
,![]() ), contribution of the subspaces
), contribution of the subspaces ![]() and
and ![]() respectively when using the concept of multiplicity of the solutions (i.e. Theorem 1) for the higher order derivatives of the energy density (see (14)). We call the total EM field
respectively when using the concept of multiplicity of the solutions (i.e. Theorem 1) for the higher order derivatives of the energy density (see (14)). We call the total EM field ![]() and
and ![]() inside the copper plate (skin layer) with associated permittivity
inside the copper plate (skin layer) with associated permittivity ![]() and permeability
and permeability![]() . They are solutions of the Maxwell equations:
. They are solutions of the Maxwell equations:
![]() (18)
(18)
with the principle of charge conservation:
![]() (19)
(19)
Now, the variation of energy density (14) together with the equation of charge conservation is formulated such as:
![]() (20)
(20)
![]() is the Poynting vector. Now, writing
is the Poynting vector. Now, writing![]() ,
, ![]() and
and ![]() is the first derivative in time (
is the first derivative in time (![]() ) (i.e. solutions in
) (i.e. solutions in![]() ), then following [15]
), then following [15]
![]() (21)
(21)
using the equalities ![]() and the Maxwell equation
and the Maxwell equation![]() ,
, ![]() the previous equation reduces to:
the previous equation reduces to:
![]() (22)
(22)
We can separate in three groups,
![]()
The Poynting vector is defined as ![]() and its derivative
and its derivative ![]() . Thus, the second order term of the energy density is the contribution of the EM field generated by
. Thus, the second order term of the energy density is the contribution of the EM field generated by ![]() and
and ![]() is:
is:
![]()
The last line is the contribution from only the fields ![]() and
and![]() .
.
Finally, the creation of the wave defined by the EM field (![]() ,
,![]() ) means that some material properties may allow to create two type of EM waves namely (
) means that some material properties may allow to create two type of EM waves namely (![]() ,
,![]() ) and (
) and (![]() ,
,![]() ).
).
4. Some Comments on the Uncertainty Principle in the Energy Parallax Theory
Uncertainty principle is generally known from the Heisenberg’s relationship in quantum mechanics. In a broad sense, uncertainty principles are a variety of mathematical inequalities asserting a fundamental limit to the precision with which certain pairs of physical properties describing a system, known as complimentary variables (e.g. position and momentum of a particle), can be known [5] [13] .
So far in our comparison between the energy parallax and the perturbation theory, the development is based on the mathematical properties of the functions in ![]() (i.e. finite energy functions) in order to guaranty the convergence of the (Taylor) series associated with those functions and/or the energy. In particular, some examples uses special type of waves (i.e. evanescent waves in Section 3.2.1 or Section 3.2.2) included in
(i.e. finite energy functions) in order to guaranty the convergence of the (Taylor) series associated with those functions and/or the energy. In particular, some examples uses special type of waves (i.e. evanescent waves in Section 3.2.1 or Section 3.2.2) included in ![]() with the application of the energy parallax on the variation of EM energy density. Thus, we emphasize that the energy function and/or the EM energy density defined for functions in
with the application of the energy parallax on the variation of EM energy density. Thus, we emphasize that the energy function and/or the EM energy density defined for functions in![]() , play a key role in both the energy parallax and perturbation theory. Here, we show with the uncertainty principles, how the variables in our system (i.e. time, frequency, wavelength) can be affected with the variations of energy quantities.
, play a key role in both the energy parallax and perturbation theory. Here, we show with the uncertainty principles, how the variables in our system (i.e. time, frequency, wavelength) can be affected with the variations of energy quantities.
Let us define the electric field E function in ![]() with variables in time t and space x. Following the definition of
with variables in time t and space x. Following the definition of![]() , one can write
, one can write
![]() (23)
(23)
defining ![]() and k the wavelength, we can further state using the Parseval-Dirichlet equality― [17] ,
and k the wavelength, we can further state using the Parseval-Dirichlet equality― [17] ,
![]() (24)
(24)
Associating the quantities ![]() and
and ![]() with
with ![]() and
and ![]() [17] , one can write the uncertainty principle in time and frequency,
[17] , one can write the uncertainty principle in time and frequency,
![]() (25)
(25)
with the relationship (modified Parseval-Dirichlet equality) ![]() inserted in (24), the uncertainty principle can be written differently
inserted in (24), the uncertainty principle can be written differently
![]() (26)
(26)
Thus, the variation of the energy quantity![]() , means that the function/wave is distorted in time or an increase of the frequency spectrum. In terms of energy parallax, if we think about the superposition of multiple waves/functions (i.e. Theorem 1), the broadening of the frequency spectrum could be interpreted as additional waves with larger (or shifted) frequency bands.
, means that the function/wave is distorted in time or an increase of the frequency spectrum. In terms of energy parallax, if we think about the superposition of multiple waves/functions (i.e. Theorem 1), the broadening of the frequency spectrum could be interpreted as additional waves with larger (or shifted) frequency bands.
Finally, if we want to look at the inequality involving the position x, one needs to use the wave-particle duality and consider the wave as a photon. In this case, we can use the Heisenberg uncertainty principle in quantum mechanics to state the relationship between x and the moment p [16] .
5. Discussion on the Woodward Effect interpreted with the Energy Parallaxtheory
The Woodward effect, also referred to as a Mach effect, is part of a hypothesis proposed by James F. Woodward in 1990 [3] . The hypothesis states that transient mass fluctuations arise in any object that absorbs internal energy while undergoing a proper acceleration. Recently, the Woodward effect was applied to asymmetric EM cavities (i.e. frustum) due to EM waves reflected on the cavity's wall, and creating a momentum [2] . The assumption is that the EM energy density variation results from the evanescent waves taking place in the skin depth of the asymmetric EM cavity’s walls.
The Woodward effect is based on a formula which the author implicitly assumed that the rest mass of the piezoelectric material via the famous Einstein's relation in special relativity ![]() (
(![]() the rest energy associated with the rest mass m) and its variation via electrostrictive effect. In order to apply this formula to an asymmetric EM cavity, the author in [2] formulated the hypothesis that the EM excitation on the walls creates electric charges (i.e. electrons) which makes the rest mass varying with time. The Woodward effect can be mathematically derived in various ways [18] [19] [20] . Note that in the appendices, we also show a derivation based on the model of a point mass particle moving in a varying electric field.
the rest energy associated with the rest mass m) and its variation via electrostrictive effect. In order to apply this formula to an asymmetric EM cavity, the author in [2] formulated the hypothesis that the EM excitation on the walls creates electric charges (i.e. electrons) which makes the rest mass varying with time. The Woodward effect can be mathematically derived in various ways [18] [19] [20] . Note that in the appendices, we also show a derivation based on the model of a point mass particle moving in a varying electric field.
If we define the mass density such as![]() , then from [20] , one can write the elementary mass variation per unit of volume
, then from [20] , one can write the elementary mass variation per unit of volume
![]() (27)
(27)
Let us define the the rest energy![]() , then
, then
![]() (28)
(28)
In some particular cases such as an EM cavity, we assume that the variation in time of the rest energy is equal to the variation of EM energy density u (i.e.![]() ), but the rest energy is much bigger than the EM energy density
), but the rest energy is much bigger than the EM energy density![]() . It allows then to state the relationship between the Woodward effect and the EM energy density
. It allows then to state the relationship between the Woodward effect and the EM energy density
![]() (29)
(29)
The EM energy density u follows the general definition of the sum of energy density from the electric (![]() ) and magnetic (
) and magnetic (![]() ) fields [15] . Note that in [2] , the author defines the Electro magnetic and gravitational coupling using equation (29).
) fields [15] . Note that in [2] , the author defines the Electro magnetic and gravitational coupling using equation (29).
Discussion (2): The above equation shows that the variation of mass density is a linear relationship with the first and second derivative of the EM energy density. To recall Example 2 in Section 3.2.2, we underline the relationship between the order of the derivatives of the EM energy density and the energy spaces. As we are dealing with evanescent waves (functions in ![]() with
with![]() , with 3D space and time) in the skin layer of the EM cavity, we can apply the results of Example 2 with the multiplicity of the solutions (i.e. Theorem 1). The interpretation of the Woodward effect using the energy parallax is that the solutions are in
, with 3D space and time) in the skin layer of the EM cavity, we can apply the results of Example 2 with the multiplicity of the solutions (i.e. Theorem 1). The interpretation of the Woodward effect using the energy parallax is that the solutions are in ![]() (k in
(k in![]() ) using the same definitions as in Section 2. In other words, we need to take into account the evanescent waves associated with the electric and magnetic fields and their first and second derivative in time.
) using the same definitions as in Section 2. In other words, we need to take into account the evanescent waves associated with the electric and magnetic fields and their first and second derivative in time.
6. Conclusions
This work is a discussion on the energy parallax and the comparison with the perturbation theory. One of the motivation is that the energy parallax is based on the multiplicity of the solutions (i.e. Theorem 1) developed by [2] for the functions in the![]() , i.e. finite energy functions in the Schwartz space
, i.e. finite energy functions in the Schwartz space![]() . Unlike the perturbation theory where the solutions are expressed in power series with the addition of small quantities to take into account the perturbation of the system’s energy, the energy parallax considers additional solutions to a given PDE (or PDEs describing a given system) based on the higher order derivatives of the primary solution when considering higher order perturbations of the system’s energy. Note that we give some meaning to the variation of energy via the uncertainty inequality (time, frequency) based on the superposition of waves using the energy parallax.
. Unlike the perturbation theory where the solutions are expressed in power series with the addition of small quantities to take into account the perturbation of the system’s energy, the energy parallax considers additional solutions to a given PDE (or PDEs describing a given system) based on the higher order derivatives of the primary solution when considering higher order perturbations of the system’s energy. Note that we give some meaning to the variation of energy via the uncertainty inequality (time, frequency) based on the superposition of waves using the energy parallax.
The perturbation theory is well defined when the system can be described with an operator (e.g., Hamiltonian) such as in quantum mechanics. However, complex systems using multiple operators or various PDEs may be best described in terms of the variation of the total energy. In this way, the energy parallax can be seen as an alternative. In the first example, the energy parallax is applied to the evanescent waves in the skin layer of a dielectric material (i.e. EM fields). We also show the possible application of this concept with the Woodward effect for the special case of the asymmetrical cavities. The energy parallax is used with the higher order derivatives of the EM energy density.
Acknowledgements
The authors would like to acknowledge people who have been involved in developing the presented model during the past two years via discussions or various feedbacks including Dr. José Rodal and Prof. Heidi Fearn (California State Fullerton University).
Appendix: Derivation of the Woodward Effect from a Point Mass Particle with a Varying Charge
In this section, we derive the Woodward effect for a particle moving along a world line in a varying electric field. It is a simplistic model of a so called “relativistic” capacitor, due to the variation of mass only dependent of the
variation of charge![]() .
.
A1. Lagrangian Formalism
Let us call ![]() and
and![]() . Thus, we assume that the Lagrangian is a function of
. Thus, we assume that the Lagrangian is a function of![]() ,
, ![]() and the time t. Now, the action principle is applied when varying the fields of the small quantity
and the time t. Now, the action principle is applied when varying the fields of the small quantity ![]() and
and ![]() The infinitesimally variation of the action is then
The infinitesimally variation of the action is then
![]() (30)
(30)
![]() is a proper interval defines along the path of the particle. In order to simplify the notation, let us define
is a proper interval defines along the path of the particle. In order to simplify the notation, let us define ![]() and
and![]() . One can further develop the equation above
. One can further develop the equation above
![]() (31)
(31)
using the same development as the Euler-Lagrange equation (and the assumption that![]() ), one can rewrite the above equation such as
), one can rewrite the above equation such as
![]() (32)
(32)
Note that the momentum ![]() is defined such as
is defined such as![]() . Now, let us state the Euler-Lagrange equation
. Now, let us state the Euler-Lagrange equation
![]() (33)
(33)
A2. The Case of the Point Mass Particle inside an Electric Field
The idea is to use the Lagrangian for a particle inside an EM field subject to a Lorentz force, but with a varying charge in time ![]() and a varying mass in time and space
and a varying mass in time and space![]() . Let us state the Lagrangian for such a system with simply the electric field (see for a full statement [21] ):
. Let us state the Lagrangian for such a system with simply the electric field (see for a full statement [21] ):
![]() (34)
(34)
![]() is the electric potential such as
is the electric potential such as![]() . The system is not conservative (off-shell variation) and thus at the first order variation of the Lagrangian we can apply (32):
. The system is not conservative (off-shell variation) and thus at the first order variation of the Lagrangian we can apply (32):
![]() (35)
(35)
Knowing that![]() , one can develop further
, one can develop further
![]() (36)
(36)
with the assumptions that![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Also with the approximation
. Also with the approximation![]() ,
, ![]() Now, if we separate the variables as internal and external parameters, such as
Now, if we separate the variables as internal and external parameters, such as ![]() are external (or parameters in on-shell transformation); and
are external (or parameters in on-shell transformation); and ![]() are the parameters due to the “relativistic” capacitor model. We can then rewrite (23) such as:
are the parameters due to the “relativistic” capacitor model. We can then rewrite (23) such as:
![]() (37)
(37)
Thus, from this equation, we can see that the first group of terms in ![]() and the second group of terms in
and the second group of terms in ![]() are with derivatives of the external variables (e.g.,
are with derivatives of the external variables (e.g., ![]() , V), whereas the two last groups of variables are with derivatives of the internal variables (e.g., m, q). Now, if we assume that
, V), whereas the two last groups of variables are with derivatives of the internal variables (e.g., m, q). Now, if we assume that![]() , in other words, a negligible displacement in space during the variation of
, in other words, a negligible displacement in space during the variation of![]() , the equation becomes
, the equation becomes
![]() (38)
(38)
and reciprocally with the assumption![]() ,
,
![]() (39)
(39)
and by definition![]() . One can set
. One can set![]() , and see the variation of mass only dependent of the variation of charge
, and see the variation of mass only dependent of the variation of charge ![]() in our “relativistic” capacitor model. Furthermore, we can get the equation without variation of the internal variables if
in our “relativistic” capacitor model. Furthermore, we can get the equation without variation of the internal variables if![]() :
:![]() .
.
As the “relativistic” capacitor model is a particle moving along a world line, one can follow the same way that Prof. Woodward used to establish the Woodward effect (See Appendix A of [3] ). Let us write the equation of the momentum when the particle is stimulated by external force:![]() . With equation (39), one can write:
. With equation (39), one can write:
![]() (40)
(40)
which ends up in
![]() (41)
(41)
This equation is the particle accelerated by a Lorentz force with only the electric field. We can qualify it as the macroscopic view of the system. One can
then define a force![]() . Making the same assumption as in [3] , one can apply the four divergence to the normalized force
. Making the same assumption as in [3] , one can apply the four divergence to the normalized force
![]() :
:
![]() (42)
(42)
with![]() , the first term of the stress energy tensor (or
, the first term of the stress energy tensor (or![]() ), which is the EM energy density. Let us make the assumption that the particle is accelerated to the speed of light
), which is the EM energy density. Let us make the assumption that the particle is accelerated to the speed of light![]() , and if the fluctuation of the total energy is equal to the fluctuation of the EM energy density (
, and if the fluctuation of the total energy is equal to the fluctuation of the EM energy density (![]() ), thus we have also
), thus we have also![]() . The above equation is then:
. The above equation is then:
![]() (43)
(43)
or
![]() (44)
(44)
Let us define the potential![]() , and rewrite the previous equation
, and rewrite the previous equation
![]() (45)
(45)
The infinitesimally variation ![]() is only due to the variation in time in the LHS term, then
is only due to the variation in time in the LHS term, then
![]() (46)
(46)
with![]() ,
,
![]() (47)
(47)
Note that it is possible to consider higher order derivatives in time if we consider the variations of the quantity ![]() at higher orders (i.e.
at higher orders (i.e. ![]() ). However, one must also consider higher order variations of
). However, one must also consider higher order variations of ![]() and q in order to agree with equation (45).
and q in order to agree with equation (45).
Also, it is worth to underline that equation (42) is established when considering only an electrical potential in the Lagrangian formalism of a point mass particle moving in an electrical field (i.e. Equation (34)). According to [21] , one can also include a magnetic potential within the Lagrangian, adding the
vector potential![]() .
. ![]() is the scalar product and
is the scalar product and ![]() is the magnetic potential. It follows that the term
is the magnetic potential. It follows that the term ![]() is added on the RHS of Equation (41) and the term
is added on the RHS of Equation (41) and the term ![]() in the LHS of Equation (42). It forces to
in the LHS of Equation (42). It forces to
do the same assumption as with the electric field in order to get an equation similar to equation (47). That is why, for the sake of the example, the addition of the magnetic potential is not so important.