Uncertainty Principle and Bifurcations in the SU(2) Nonlinear Semiquantum Dynamics ()
1. Introduction
Semiquantum Dynamics (SD) may be used to describe systems in which quantum and classical degrees of freedom coexist. One finds in [1] an exhaustive compilation of physical phenomena and technological applications successfully modeled by SD. It is also possible to encounter situations in which SD is used to describe physical phenomena [2] [3] [4] [5] . A nonlinear semiquantum Hamiltonian associated to the SU(2) Lie algebra is very useful to model the problem of quantum confinement, which is of interest for nanotechnology and solid state physics. In particular, if the quantum subsystem is associated to the SU(2) Lie algebra generators
, the uncertainty principle (UP) adopts a very simple form and turns out to be a motion invariant [6] .
In [7] , the authors consider the following semiquantum Hamiltonian
(1)
where
and
are quantum operators, the x and z components of a 1/2 spin particle, while q and p are canonical conjugated classical variables (position and momentum) that obey the Hamilton equations [5] [8] . B, C, m, D, and F are positive and constant parameters. The Hamiltonian given by Equation (1) represents a quantum 1/2 spin particle interacting with an external magnetic field [2] [7] (due to the term
). The particle is confined by the double well
potential
, generated by a classical particle of mass m and it undergoes elastic reflections between the moving frontier,
, of the double well potential. The term
represents the classical kinetic energy. The clas-
sical and quantum variables are couple in non-linear fashion via the term,
,
being the coupling constant. In [7] , the authors concentrate on the likely presence of chaotic motion (semiquantum chaos) for special values of the coupling strength. The authors represent the trajectories for different initial conditions by stroboscopic plots, displaying regular and irregular dynamics. This Hamiltonian also may be reduced to the one in [2] (taking
). It also can be used to model the semiquantum differential equations of the spin-boson Hamiltonian of [9] (taking
). In [10] , the authors considered the simplest case of a spin-boson Hamiltonian, i.e., a two level system coupled to one oscillator degree of freedom, and made a posterior semiclassical approximation, to obtain a semiquantum Hamiltonian similar to that given by Equation (1).
We consider that, since the Hamiltonian of Equation (1) is able to model the quantum confinement phenomenon, its dynamics deserves an exhaustive analysis. In the present work, we purport to give a full description of its phase space taking into account that, in conservative systems like this one, the motion is fully determined by the amount and disposition of its fixed points. We make a complete characterization of them and determine their stability according to the system’s parameters values. In addition, we obtain the bifurcation curves which divide the phase space into the three different zones in which the fixed points are located, according to their stability. We present a dimensionless formulation, and because the uncertainty principle (UP) is an invariant of the motion for the nonlinear semiquantum Hamiltonians associated to the SU(2) Lie algebra [6] [11] , we make a change of variables that removes it as external strong constrain to the system’s motion equations. The UP provides then just an additional parameter in the concomitant new motion equations. We mention that, in [10] , a similar method is used for a coupled quasiparticle-oscillator system, which enables the authors to study the existence of fixed points and bifurcation curves, allowing for a formulation in canonically conjugate variables of the excitonic subsystem. In our case, the change of variables offers some advantages which are highlighted in describing our treatment and summarized in the conclusions.
2. Equations of Motion
If we consider the generators of the SU(2) Lie algebra,
, it can be easily seen that they close a partial Lie algebra under commutation with the Hamiltonian of Equation (1), since the commutator of any
with
may be expressed as a linear superposition of these generators. The semiquantum equations of motion are obtained through the Maximum Entropy Approach (MEP), using the MEP density operator
to evaluate the Hamiltonian’s mean value,
which, in turn, plays the role of a Hamilton function so as to obtain the (evolution) differential equations of motion corresponding to the classical degrees of freedom q and p (the prescription given by the MEP, in order to find the density operator, is a standard procedure. The interested reader can consult [6] [12] [13] [14] to become familiar with the subject). The MEP density operator
corresponds to a non-pure state given that it is constructed from a set of noncommuting observable
(the generators of the SU(2) Lie algebra).
Following the prescription given in [6] [12] [13] , we obtain the equations of motion for the system given by Equation (1):
(2)
(3)
(4)
(5)
(6)
and they must obey the uncertainty relation [6] [11] which, for the SU(2) Lie algebra case, adopts the form [6] :
(7)
We will consider the whole range of values that the polarization vector
can achieve in the interval
, given that the generators of the SU(2) Lie algebra
constitute a complete set of noncommuting observables. Thus, we are dealing with a non pure quantum state
. Equation (7) defines the well-known Bloch sphere, whose “radius’’,
, remains a constant of the motion while its possible values
are determined by the initial conditions imposed on Equations (2)-(6). It is also taken into account that the system’s energy (evaluated via the non pure state density operator
) [6] [13] :
(8)
must remain a constant of motion during the whole temporal evolution [6] .
In order to find the fixed points it is convenient to express Equations (2)-(6), (7), and (8) in dimensionless form [15] , by defining new variables,
and
:
(9)
with
(10)
Accordingly, Equations (2)-(6) and (7) become:
(11)
(12)
(13)
(14)
(15)
(16)
and from Equation (8) the system’s energy reads:
(17)
3. The System’s Fixed Points
In order to determine the system’s fixed points we proceed, as usual, by equating (11)-(15) to zero. Note that the existence of them does not depend on the parameter
, but only on the values of r and s. From Equation (13), there exist two situations: the cases
and
.
3.1. Case q* = 0
From
in Equation (11), it follows
. From
in Equation (12), it follows
. So, from Equation (16), we are led to
. From
in Equation (14), it follows
. Therefore, in this case, one obtains
two fixed points,
, where
,
and
being the north and south pole of the dimensionless Bloch sphere.
3.2. Case q*
0
From Equations (11)-(15) it follows that these kinds of fixed points must fulfill:
(18)
so they adopt the appearance
, and must obey the strong constraint given by Equation (16), the uncertainty principle, which in terms of
, reads:
(19)
with
,
. Thus,
are the roots of Equation (19), which should be tackled numerically. The system’s phase space, given by Equations (11)-(15), is five-dimensional. However, the Jacobian matrix at the fixed point must have, at least, one null eigenvalue, since the uncertainty condition of Equation (16) is an external constraint added to the equations of motion. This means that, in fact, the solutions lie on a 4D invariant manifold,
.
Accordingly, we represent the quantum degrees of freedom,
, in spherical coordinates:
(20)
with
,
,
and we study the system’s fixed points by means of the four-dimensional variables,
.
Using the relations:
(21)
we find:
(22)
The system of Equations (11)-(16) becomes now:
(23)
(24)
(25)
(26)
where
means
, and
. The system’s energy given by Equation (17) becomes:
(27)
We claim that this change of variables (CV) offers some advantages:
1) The quantum variables
and
obey the relationship:
(28)
as if they were canonical spherical-conjugates, meanwhile the classical ones, q and p, obey, as usual, the Hamilton’s equations [6] [13] :
(29)
Thus, the fixed points
of the system given by Equations (23)-(26), are the critical points of the energy function
of Equation (27), since:
(30)
2) The uncertainty relation in Equation (16), now of the form
, is incorporated into the new system’s equations in a natural way by reducing the system dimension and removing a superfluous null eigenvalue. One may speak of linearization of the original system at each fixed point.
3) Our CV provides a better characterization of the fixed points, since with this change we find a generic expression for them explicitly written in terms of the variable q. This fact facilitates the study of 1) the presence of bifurcations curves in the parameter’s space, and 2) the stability analysis of the fixed points.
To obtain the fixed points,
, we equate (23)-(26) to zero. From
in Equation (25), it follows that
, and from
in Equation (24), we are led to
or
,
.
3.2.1. Case
From
in Equation (23) and
, it follows that:
(31)
so that:
(32)
Then, in this case,
adopts the generic form
. From Equation (32),
, and
. Since
, then:
(33)
From
in Equation (26) and
one has:
(34)
and then:
(35)
Replacing Equation (33) into Equation (35), it follows that
must be the solution of the following equation:
(36)
Since
, the right side on Equation (36) is positive. Thus, the possible values of
are restricted to the range
. In each case, the amount of solutions will be obtained graphically by means of the intersection points of two curves, namely:
(37)
・
. Figure 1 depicts the intersection between the left branch of
and
. It is possible to see that for all
, there is always a unique solution,
, in the range of interest, and so a corresponding fixed point,
, is obtained. Note also that this point does not bifurcate in the
-parameter space.
・
. Here, we are looking for the intersection points of the right branch of
and
. The situations for different values of r and s are depicted in Figure 2, by considering r as a “fixed’’ parameter and s going down from
to
.
![]()
Figure 1. The graph of the functions g and the left branch of f of Equation (37) for
, showing the unique intersection point 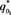 existing for
existing for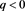 .
.
For![]() , Figure 2(a) and Figure 2(b) show that the two curves intersect at one point at
, Figure 2(a) and Figure 2(b) show that the two curves intersect at one point at![]() , this being the unique solution of Equation (36) in the range of interest, adding a new fixed point,
, this being the unique solution of Equation (36) in the range of interest, adding a new fixed point,![]() .
.
Decreasing the s value, the curves become tangent at![]() , at the critical value
, at the critical value![]() . Note that s is a “rigid’’ parameter since only produces f graph shifts, in contrast to the “flexible’’ parameter r which bends the graph of g. The scenario splits into two ones when
. Note that s is a “rigid’’ parameter since only produces f graph shifts, in contrast to the “flexible’’ parameter r which bends the graph of g. The scenario splits into two ones when![]() , depending on the convexity of g as compared to the f value at
, depending on the convexity of g as compared to the f value at![]() , i.e., depending on the absolute values of the second derivatives:
, i.e., depending on the absolute values of the second derivatives:
![]() (38)
(38)
Thus, for ![]() (
(![]() , see Figure 2(c)), there is no intersection point between f and g. However, for
, see Figure 2(c)), there is no intersection point between f and g. However, for ![]() but
but ![]() (
(![]() , see Figure 2(d)), the graphs intersect at a new point,
, see Figure 2(d)), the graphs intersect at a new point, ![]() , giving rise to another solution in the range of interest. This fact makes the line
, giving rise to another solution in the range of interest. This fact makes the line ![]() to be a codimension-1 bifurcation curve in the
to be a codimension-1 bifurcation curve in the ![]() -parameter space: an imperfect saddle-node bifurcation occurs for
-parameter space: an imperfect saddle-node bifurcation occurs for![]() , since the fixed point
, since the fixed point ![]() is lost, and another imperfect saddle-node bifurcation occurs for
is lost, and another imperfect saddle-node bifurcation occurs for![]() , since a new fixed point,
, since a new fixed point, ![]() , is created (the term “imperfect” means that only one point is created/extinguished, instead of two, as would happen in a “perfect” saddle-node. This is due to the loss of the quadratic symmetry of
, is created (the term “imperfect” means that only one point is created/extinguished, instead of two, as would happen in a “perfect” saddle-node. This is due to the loss of the quadratic symmetry of ![]() when considering only its right branch (
when considering only its right branch (![]() ) [15] .
) [15] .
This last scenario (![]() ) persists until the two graphs becomes tangent again at the critical value
) persists until the two graphs becomes tangent again at the critical value![]() , when
, when ![]() and
and ![]() meet each other at
meet each other at![]() , with
, with ![]() the tangency point. For s below this critical value
the tangency point. For s below this critical value![]() , the two graphs do not match any longer, and the fixed points
, the two graphs do not match any longer, and the fixed points ![]() and
and ![]() are mutually destroyed. The system undergoes a (“perfect”) saddle-node bifurcation at
are mutually destroyed. The system undergoes a (“perfect”) saddle-node bifurcation at![]() , and this makes the relation
, and this makes the relation ![]() to be another codimension-1 bifurcation curve in the
to be another codimension-1 bifurcation curve in the ![]() -parameter space. Note the fundamental role that plays the uncertainty principle parameter r in the coming into being of these bifurcation curves.
-parameter space. Note the fundamental role that plays the uncertainty principle parameter r in the coming into being of these bifurcation curves.
To find the relation ![]() at
at![]() , we proceed by equating the first derivatives:
, we proceed by equating the first derivatives:
![]() (39)
(39)
From this, we obtain the relation between ![]() and r:
and r:
![]() (40)
(40)
valid for![]() . Evaluating f and g at Equation (40), and so equating
. Evaluating f and g at Equation (40), and so equating ![]() to
to![]() , we find the relation between r and s:
, we find the relation between r and s:
![]() (41)
(41)
or, equivalently,
![]() (42)
(42)
Replacing Equation (41) into Equation (40), we find the relation between ![]() and
and![]() , that allows to better fit the possible ranges for
, that allows to better fit the possible ranges for ![]() and
and![]() , within the range
, within the range![]() , which will be useful later on:
, which will be useful later on:
![]() (43)
(43)
or, equivalently:
![]() (44)
(44)
Thus, as ![]() (Figure 2(d)), we have for
(Figure 2(d)), we have for![]() :
:
![]() (45)
(45)
Note that the bifurcation curve ![]() meets the line
meets the line ![]() tangentially at a codimension-2 point
tangentially at a codimension-2 point ![]() in the
in the ![]() -parameter space (Figure 3).
-parameter space (Figure 3).
3.2.2. Case ![]()
From ![]() in Equation (23) and
in Equation (23) and![]() , it follows that:
, it follows that:
![]() (46)
(46)
Accordingly, in this case ![]() adopts the generic form
adopts the generic form![]() . Equation (33) is still valid, but from
. Equation (33) is still valid, but from ![]() in Equation (26) and
in Equation (26) and![]() , one has:
, one has:
![]() (47)
(47)
Replacing (33) into (47), it follows that ![]() must be the solutions of the equation:
must be the solutions of the equation:
![]() (48)
(48)
Accordingly, in this case the possible values of ![]() are restricted to the range
are restricted to the range![]() . Therefore, the solutions should now be obtained by the intersection points of the functions
. Therefore, the solutions should now be obtained by the intersection points of the functions ![]() and
and ![]() (defined in (37)) according to the r and s values. It is easy to see that, for symmetry reasons, the analysis is completely analogous to the one developed in the previous Section. Then, the solutions thus obtained are:
(defined in (37)) according to the r and s values. It is easy to see that, for symmetry reasons, the analysis is completely analogous to the one developed in the previous Section. Then, the solutions thus obtained are: ![]() for all
for all![]() ,
,
![]()
Figure 3. The ![]() -parameter space and the codimension-1 bifurcation curves: the
-parameter space and the codimension-1 bifurcation curves: the ![]() and
and ![]() for r > 2, that meet tangentially at the codimension-2 point
for r > 2, that meet tangentially at the codimension-2 point![]() . The number labeling each region indicates the quantity of non-degenerate fixed points. Cyan:
. The number labeling each region indicates the quantity of non-degenerate fixed points. Cyan:![]() ,
, ![]() ,
, ![]() ,
,![]() ; orange:
; orange:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ; violet:
; violet:![]() ,
,![]() .
.
![]() for
for![]() ,
, ![]() for
for
![]() , and the same bifurcation curves,
, and the same bifurcation curves, ![]() and
and![]() , are found. Note also that
, are found. Note also that![]() .
.
Summing up, the amount of fixed points in the ![]() -plane is (Figure 3):
-plane is (Figure 3):
・ ![]()
・ ![]()
4. The Stability of the Fixed Points
The system given by Equation (1) (and then by Equation (27)) is conservative. Thus, the local behavior at the fixed point may be studied by considering the energy ![]() of Equation (27) as a function of
of Equation (27) as a function of![]() ,
, ![]() , which is a constant of motion, since
, which is a constant of motion, since![]() . The h-level sets,
. The h-level sets, ![]() , are 3D invariant manifolds containing orbits given by the equations of motion. The h-level sets help in understanding the structure of the system’s phase space. The local behavior around a fixed point will be determined by the index k of
, are 3D invariant manifolds containing orbits given by the equations of motion. The h-level sets help in understanding the structure of the system’s phase space. The local behavior around a fixed point will be determined by the index k of ![]() as a non-degenerate critical point of the Morse function
as a non-degenerate critical point of the Morse function ![]() [16] .
[16] .
Definition 1. The instability index ![]() is the number of negative
is the number of negative
eigenvalues of the Hessian matrix of ![]() at
at![]() ,
, ![]()
(whenever ![]() is a non-degenerate critical point, i.e.
is a non-degenerate critical point, i.e.![]() ).
).
This is to say, k is the number of independent directions along which ![]() decrease from
decrease from![]() . Therefore, if
. Therefore, if![]() , the h-level set around
, the h-level set around![]() , corresponds to a positive definite quadratic form,
, corresponds to a positive definite quadratic form, ![]() is a local minimum of
is a local minimum of ![]() and a system’s nonlinear center. If, in our case,
and a system’s nonlinear center. If, in our case, ![]() ,
, ![]() it is unstable, and of the saddle type.
it is unstable, and of the saddle type.
4.1. Obtaining the Index k of ![]()
From Equation (27) the Hessian matrix of ![]() at
at ![]() is:
is:
![]() (49)
(49)
Since ![]() is a square-block diagonal matrix, its eigenvalues are those from the block submatrices. Taking into account that for a
is a square-block diagonal matrix, its eigenvalues are those from the block submatrices. Taking into account that for a ![]() -matrix the eigenvalues may be written in terms of its trace and determinant, we have, then, that the four eigenvalues of
-matrix the eigenvalues may be written in terms of its trace and determinant, we have, then, that the four eigenvalues of ![]() are:
are:
![]() (50)
(50)
where ![]() and
and![]() , are the trace and determi-
, are the trace and determi-
nant of the block![]() , respectively. The instability index is, then,
, respectively. The instability index is, then,
![]() .
.
From Equation (26), ![]() , from Equation (32),
, from Equation (32), ![]() for
for![]() , and from Equation (46),
, and from Equation (46), ![]() for
for![]() . Therefore, the matrix in Equation (49) for
. Therefore, the matrix in Equation (49) for![]() , is thus expressed in terms of
, is thus expressed in terms of![]() :
:
![]() (51)
(51)
and for![]() ,
, ![]() is the same except that
is the same except that![]() .
.
The eigenvalues ![]() of Equation (50) in terms of
of Equation (50) in terms of ![]() read:
read:
![]() (52)
(52)
guaranteeing ![]() for all
for all![]() , as befits to a conservative system which cannot posses a completely unstable critical point.
, as befits to a conservative system which cannot posses a completely unstable critical point.
![]() (53)
(53)
Note that ![]() because
because![]() , and also,
, and also, ![]() from Equation (19). For
from Equation (19). For![]() :
:
![]()
and using Equation (45), it follows that
![]() (54)
(54)
From Equation (50), if![]() , it follows that
, it follows that ![]() and
and![]() . Thus, for
. Thus, for![]() , we can just conclude, from Equations (52)-(54), that
, we can just conclude, from Equations (52)-(54), that ![]() For the remaining critical points, things depends on the sign of
For the remaining critical points, things depends on the sign of ![]() in the corresponding intervals:
in the corresponding intervals:
![]() (55)
(55)
Then, from Equations (50), (54) and (55), ![]() ,
, ![]() , and therefore, from Equations (52)-(55), it follows that
, and therefore, from Equations (52)-(55), it follows that ![]() (nonlinear centers), and
(nonlinear centers), and![]() . The summary of results is displayed in Table 1.
. The summary of results is displayed in Table 1.
Figure 4 and Figure 5 illustrate a case relative to the orange zone in Figure 3, for which the six fixed points coexist (![]() ).
).
![]()
Figure 4. The ![]() components of six fixed points
components of six fixed points ![]() in the orange-zone of Figure 3, represented in the dimensionless Bloch sphere, for
in the orange-zone of Figure 3, represented in the dimensionless Bloch sphere, for![]() ,
,![]() . Blue: the arc
. Blue: the arc![]() , red: the arc
, red: the arc![]() . The projection of trajectories, starting at an initial condition close to each
. The projection of trajectories, starting at an initial condition close to each![]() , is also plotted (only for
, is also plotted (only for![]() , for symmetry and clarity reasons) displaying the local behavior, according to the corresponding index k (we use
, for symmetry and clarity reasons) displaying the local behavior, according to the corresponding index k (we use![]() ). The degenerate points, PN and PS, are plotted in black.
). The degenerate points, PN and PS, are plotted in black.
4.2. Note
The other two fixed points of the system, ![]() , which are not described by the change of variables (
, which are not described by the change of variables (![]() ), result degenerate critical points of the energy
), result degenerate critical points of the energy ![]() of Equation (17) as a function of
of Equation (17) as a function of![]() , since they force the vanishing of the Hessian matrix of
, since they force the vanishing of the Hessian matrix of![]() .
.
5. Conclusions
The dimensionless formulation of Equations (2)-(6), given by Equations (11)-(15), allows for reduction in the number of system’s parameters to three: r, s, and![]() . The posterior change of variables (CV) has additional advantages as highlighted before: the reduction of the system’s dimension through proper consideration of the uncertainty principle constraint. It also affords a convenient way to obtain the fixed points, providing a better characterization of them, according to the system’s parameters, and depending only on the classical degree of freedom, q. We can display a relation between the new quantum degrees of freedom,
. The posterior change of variables (CV) has additional advantages as highlighted before: the reduction of the system’s dimension through proper consideration of the uncertainty principle constraint. It also affords a convenient way to obtain the fixed points, providing a better characterization of them, according to the system’s parameters, and depending only on the classical degree of freedom, q. We can display a relation between the new quantum degrees of freedom, ![]() and
and![]() , which turn out to be canonically “spherical-conjugates”, making the system’s fixed points to be the critical points of the energy function
, which turn out to be canonically “spherical-conjugates”, making the system’s fixed points to be the critical points of the energy function![]() . In addition, the CV illustrates the role of each parameter in the system dynamics in a very clear fashion:
. In addition, the CV illustrates the role of each parameter in the system dynamics in a very clear fashion: ![]() can only play a role in the stability analysis, ensuring that the unstable fixed points are saddles. The parameter s accounts for the range of possible values that q can achieve at each fixed point, dividing the phase space into three regions. Finally, the parameter r forces the uncertainty principle to play a fundamental role in the appearance/disappearance of fixed points, thus governing the presence of bifurcations in the SU(2) nonlinear semiquantum dynamics.
can only play a role in the stability analysis, ensuring that the unstable fixed points are saddles. The parameter s accounts for the range of possible values that q can achieve at each fixed point, dividing the phase space into three regions. Finally, the parameter r forces the uncertainty principle to play a fundamental role in the appearance/disappearance of fixed points, thus governing the presence of bifurcations in the SU(2) nonlinear semiquantum dynamics.
The putative presence of chaotic dynamics in this system, for some ![]() - parameter’s region, is still under consideration and will be reported elsewhere.
- parameter’s region, is still under consideration and will be reported elsewhere.
Remark: by virtue of the SU(2) Lie algebra, the uncertainty principle becomes a constant of the motion. Thus, we claim that the methodology used in the present work applies even in the case in which the quantum subsystem of Equation (1) was nonlinear in the spin variables (as in the non-dissipative Hamiltonian case treated in [17] , which can be used to model a SQUID). Despite the nonlinearity in the quantum subsystem, the uncertainty principle would remain there a constant of the motion. This and other topics related to semiquantum dynamics will be part of future work.
Acknowledgements
The authors would like to thank the reviewers for their suggestions to improve the readability of the paper. C. Sarris dedicates this work to Professor Araceli Proto, in memoriam. This work was partially supported by Programación Cientfica UBACyT 2014-2017 (20020130200093BA GEF), Ministerio de Educación, Argentina.