Efficient Harmonic Analysis Technique for Prediction of IGS Real-Time Satellite Clock Corrections ()
1. Introduction
Since 1994, the “International GNSS Service” (IGS) produces precise ephemerides, which includes satellite coordinates and clock corrections at equidistant epochs, typically 15 minutes. Precise ephemerides can be obtained from the IGS website (https://igscb.jpl.nasa.gov/). Precise ephemerides accuracies vary depending on availability. For example, the ultra-rapid precise ephemerides are available in real-time through the predicted part, the rapid precise ephemerides are available with latency about 17 - 41 Hours, and the final precise ephemerides is available with delay about 12 - 18 days [1] . IGS final products enable users to achieve centemeter-level accuracy if the IGS conventions are considered [2] . However, this accuracy is achievable only in post-processing rather than in real-time. The only precise product that available to users in real-time is the predicted part of the IGS ultra-rapid products (IGU). However, the accuracy which can be obtained using the predicted part is much less than that can be obtained from products derived from real measurements [3] . In 2001, the “Real-Time Working Group” (RTWG) was established by the IGS, in order to meet requirements of precise real-time applications, and defined the framework for “Real-Time Service” (RTS). In August 2011, the IGS RTS project started providing access to real-time satellite precise orbit and clock corrections in addition to raw GNSS data by streaming via internet. The IGS RTS is officially launched in April 1st, 2013.
RTS utilizes the main infrastructure of the IGS, including global network stations (see Figure 1), data centers in additional to analysis centers. Currently, eight analysis centers are participating in RTS products, namely, BKG, CNES, DLR, ESA/ESOC, GFZ, GMV, NRCan, and WUHAN. NRCan represents the RTWG chair, ESOC represents the “Real Time Analysis Center Coordinator” (RTACC), and BKG represents the coordinator of the RTS data flow. The final streams of the RTS products represent the combined solution generated by processing individual solutions from different RTAC. Both ESA and BKG analysis centers represent the RTS combination centers.
IGS01/IGC01 is a single-epoch combined solution in which no filters are applied, and each epoch is independent of the other. IGS01 product refers to “Antenna Phase Center” (APC), while the IGC01 refers to satellite “Center of Mass” (CoM). IGS02, on the other hand, is a combined solution using Kalman filter. The orbit in this case is one of the IGU solutions, which refers to satellite APC. Both IGS01/IGC01 and IGS02 include corrections to the GPS system only. However, IGS03 includes GLONASS corrections in addition to GPS corrections.
RTS corrections are expressed within the “International Terrestrial Reference Frame 2008” (ITRF08). To broadcast the RTS corrections, users have to register through the IGS RTS web page (http://igs.org/rts) and download the NTRIP client application from e.g., BKG analysis center web page (http://igs.bkg.bund.de/ntrip/download). The real-time orbital corrections are expressed in the orbital coordinate system (radial, along-track, and cross-track). So, to apply the RTS orbital corrections, it should be computed at the current epoch using the rate of change of each component and then transformed to “Earth Centered Earth Fixed” (ECEF) components. RTS clock corrections, on the other hand, are streamed as polynomial coefficients and can be computed at the current epoch from the corresponding values at the issue of data time (IOD). The standard deviation of the IGS RTS clock corrections is ten times better than the IGU clock corrections. Moreover, the PPP solution using the IGS RTS products can improve the RMS of the estimated coordinates by about 50% [4] .
Real-time streaming of the RTS corrections is the key to maintain the above- mentioned accuracies. However, unintentional streaming interruption may happen for many reasons such as software or hardware failure. Streaming interruption, if happened, will cause sudden degradation of the obtained solution if only the broadcast ephemerides is used. A better solution can be obtained in real-time if the IGU orbit and clock corrections are used. In this paper, a method to predict the IGS RTS corrections using historical broadcasted data is introduced. It is shown that the solution obtained using the predicted RTS clock corrections is better than that obtained from the IGU products.
2. Harmonic Analysis Technique
In practice, it is usually common to use trigonometric polynomials to represent data sets that experience periodic nature as a type of harmonic analysis. Any periodic signal can be presented by a trigonometric series as follows [5] :
(1)
where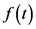 
is the approximated value at time t, 
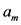and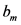 
are coefficients, N is the number of collocation points which may be different for each satellite,
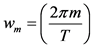in which T is the period of f, 
,
(2)
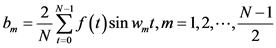(3)
Several techniques can be used to estimate the constant term 
and the coefficients 
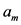and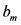 
such as Fourier Transform (which is applied here) or Least Squares Spectral Analysis (LSSA) [6] . The constant term represents the average value of the time series over one period. The coefficient 
represents two times the average value of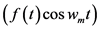 
over one period. The coefficient 
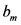represents two times the average value of 
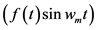over one period.
3. Analysis of Predicted Clock Corrections
The trigonometric method is used to fit four hours of the IGS RTS clock corrections collected in several sessions during GPSW 1842, then the coefficients are used to predict two hours of such corrections for all satellites. If the IGS RTS clock corrections are considered as targets, the error in the IGU clock corrections can be computed after removing the common offset and trend. Fitting and prediction errors of the predicted clock corrections (PRD) are computed during the period of study for all satellites. Figure 2 shows the results for DOY121, 2015. Moreover, statistical analysis of the IGU errors, fitting errors, and prediction errors are summarized in Table 1.
From Figure 2 and Table 1, the average value of the maximum fitting error of all satellites is about 10.57 cm and the average value of the maximum prediction error of all satellites is about 14.24 cm. However, the average value of the maximum error in the IGU clock corrections of all satellites is about 18.51 cm. The average error of PRD clock corrections is less than the average error of the IGU clock corrections because the PRD clock corrections are predicted from the real-time clock corrections, which are ten times better than the IGU clock corrections. To investigate the effect of the length of prediction time on the accuracy of the predicted clock corrections, the prediction period (two hours) is divided to 12 sessions, 10 minutes each. The standard deviation of each session is computed. Figure 3 shows the standard deviation during the two hours.
It is clear also from Figure 2 and Figure 3 that there is no deterioration in the accuracy of the PRD clock correction during the predicted two hours. From this analysis, we can expect that the performance of the PRD clock correction will be superior to the IGU clock corrections.
![]()
Figure 2. IGU clock error, fitting error, and prediction error compared with the IGS RTS clock corrections, DOY121, 2015.
![]()
Figure 3. Standard deviation of the predicted clocks over two hours.
![]()
Table 1. summary of the average statistics of fitting, prediction, and IGU clock errors.
4. PPP Mathematical Model
After prediction of RTS satellite clock corrections, two options are available to perform PPP in real-time. The first option is to use the predicted clock corrections (PRD) along with the IGU orbit. The second option is to use the IGU orbit and clock corrections. Beside the previously statistical analysis, positioning performance can be used as a measure for the quality of both PRD and IGU products. The mathematical model of the first-order ionosphere-free linear combination of pseudorange and carrier phase can be given as follows [4] :
![]()
(4)
![]()
(5)
where, ![]()
are the first-order ionosphere-free code and carrier phase combinations, ![]()
is the true geometric distance between satellite and receiver antenna phase centers (m), ![]()
is the speed of light in vacuum (m/sec), Td is the slant tropospheric delay, ![]()
are the receiver and satellite clock errors, ![]()
, ![]()
, ![]()
are the ambiguity integer numbers of L1 and L2 ambiguities, ![]()
are the first-order ionosphere-free noise including multipath and residual orbit combination.
To test the predicted clock corrections, GPS data from several IGS stations is processed in kinematic mode (Figure 4). The inputs are the first-order
![]()
Figure 4. IGS stations used to test the predicted clock corrections.
ionosphere-free code and carrier phase. The IGU orbit is used to account for satellite orbit and APC corrections are applied. Satellite clock corrections are accounted for using the PRD or the IGU clock corrections. The “Global Pressure and Temperature 2” (GPT2) model is used to account for dry tropospheric delay [7] and [8] . However, wet tropospheric delay component is estimated as an additional unknown. Vienna Mapping Function 1 (VMF1) is used for zenith tropospheric delay mapping to each satellite elevation angle [9] and [10] . All remaining errors, including sagnac, Earth tides, carrier phase windup, ocean loading, and relativity are modelled by existing models [2] . Processing is performed through three scenarios. The first, which is used as a reference, is to use the RTS products during the full session processing. The second scenario is to use the RTS products during the first 30 minutes and continue with the predicted part of the IGU products. The third scenario is the same as the second, but the PRD clocks along with the predicted part of the IGU orbit. The last two scenarios are to overcome RTS broadcasting outage. All scenarios are performed using different situations depending upon the outage period. The outage periods considered for this study are 5, 10, 15, 20, and 30 minutes. Table 2 summarizes the average positioning error in latitude, longitude, and ellipsoidal height coordinates for both IGU and PRD data processed under different outage conditions.
As can be seen in Table 2, the positioning performance of the PRD is better than that of the IGU clock corrections. The average improvement of using the PRD clocks rather than using the IGU clocks is about 80% in horizontal and three dimensional (3D) directions. Moreover, Figures 5-7 show the average root-mean-squares (RMS) of the estimated coordinates.
Our results showed that the average RMSs of the estimated coordinates are 0.09 m, 0.19 m, and 0.19 m in latitude, longitude, and height directions, respectively can be obtained when using our predicted satellite clock corrections. Using the IGU clock corrections, on the other hand, can produce RMSs of 0.34 m, 0.47 m, and 0.70 m in latitude, longitude, and height directions, respectively. These results mean an average improvement of about 72%, 58%, and 72% in latitude, longitude, and height directions, respectively. Moreover, Figures 5-7 show that
![]()
Table 2. Positioning performance of IGU and PRD clock corrections.
![]()
Figure 5. Latitude RMS of IGU and PRD clock solutions at different prediction periods.
![]()
Figure 6. Longitude RMS of IGU and PRD clock solutions at different prediction periods.
![]()
Figure 7. Ellipsoidal height RMS of IGU and PRD clock solutions at different prediction periods.
RMSs of the estimated coordinates, using our predicted clocks, is stable regardless the prediction period (5 to 30 minutes) which is not the case when using the IGU clock corrections. Such improvement is attributed to the quality of PRD clock corrections compared with the IGU clock corrections (see Figure 2 and Figure 3).
5. Conclusion
In this paper, the IGS RTS clock corrections are predicted with harmonic analysis technique using historical broadcasted data. We found that the RMSs of the predicted clock corrections are stable over a prediction time of two hours. It is shown that using the predicted clock corrections improves the RMS of the estimated coordinates by about 72%, 58%, and 72% in latitude, longitude, and height directions, respectively compared with the solution of the IGU clock corrections. Moreover, the 2D and 3D error is reduced by about 80% compared with the IGU clock corrections. Such improvement is mainly attributed to the quality of the predicted clock corrections as it is predicted from RTS clock corrections, which are ten times better than the predicted ultra-rapid clock corrections.