Numerical Approximation to Nonlinear One Dimensional Coupled Reaction Diffusion System ()
1. Introduction
Fisher and Kolmogorov Petrovsky Piscounov founded quasilinear partial dif- ferential equation which represents reaction diffusion phenomena [1] [2] , which play important rule in population dynamics as propagation of beneficial genes; mathematical description to this phenomena is as follows [1] [2] [3] ,
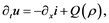 (1)
(1)
here, x declares spatial coordinate position with time t, also  is the term used to identify the population density, i is the flux associated to population, and
is the term used to identify the population density, i is the flux associated to population, and  is a limited to originator term that illuminate the net rate of production or growth in the populated area or density associated to population [3] . The be- haviour of the diffusion is accounted in the flux i, inclines by Fick’s law,
is a limited to originator term that illuminate the net rate of production or growth in the populated area or density associated to population [3] . The be- haviour of the diffusion is accounted in the flux i, inclines by Fick’s law,
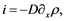 (2)
(2)
where the assumption on the diffusion coefficient D, is to be constant [3] . It is frequently to imitate the law, which is known as the Pearl-Verhulst logistic law,
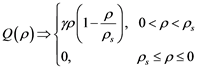 (3)
(3)
related to stranded scale to growth in the population [3] . This law explains the that initially population would grow with homogeneous fashion with time of 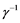 until that growth reach at some stranded level with some saturation in population [3] . Fisher and KPP were very much keen about the speed that exists in advantageous genes to propagate and they found a travelling wave solution to Equations (1), (2), (3) [3] , such solution related to velocity
until that growth reach at some stranded level with some saturation in population [3] . Fisher and KPP were very much keen about the speed that exists in advantageous genes to propagate and they found a travelling wave solution to Equations (1), (2), (3) [3] , such solution related to velocity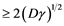 . Con- sequential, Kametaka (1976) and Uchiyama (1977)] remarks about velocity of
. Con- sequential, Kametaka (1976) and Uchiyama (1977)] remarks about velocity of 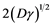 developed initial conditions (ICs), categorised as [3] ,
developed initial conditions (ICs), categorised as [3] ,
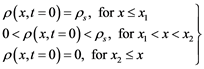 (4)
(4)
2. Governing Equation
In the year of 1948 El’ dovich, raised the major features of the diffusion reaction semi-linear equation which make useful contribution to wave of advantageous genes which are now totally classify as in the dynamics of the gas and flame with chemical kinetics [3] . Mostly, in process of combustion, the concept of heat which is channelized by the conduction processed by heat related to molecules which moves from the hot part of flame to coolant side [3] , by a particular locality, the rate of the chemical reaction such as exothermic chemical reaction (due to presence of heat), totally aware of temperature of the related gas mixture [3] . The coefficients associated with molecular diffusion and thermal are at same level of scaled, the temperature and concentration are situated almost isobaric [3] . The quantity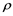 , then can represent either the temperature or concentration, without confusion, and is often referred to as the “combustion completeness by such coefficient” by Vulis, 1961 [3] . Equations (1)-(4) are then hired to modelled this attractive phenomena as a result of travelling wave nature of the flame exists in combustion process or zone, i.e. the transition layer between the region of burnt gas and the gas where combustion has not yet begun [3] . Above literature review, leads to the following reaction-diffusion system in two components along single direction, is as follows,
, then can represent either the temperature or concentration, without confusion, and is often referred to as the “combustion completeness by such coefficient” by Vulis, 1961 [3] . Equations (1)-(4) are then hired to modelled this attractive phenomena as a result of travelling wave nature of the flame exists in combustion process or zone, i.e. the transition layer between the region of burnt gas and the gas where combustion has not yet begun [3] . Above literature review, leads to the following reaction-diffusion system in two components along single direction, is as follows,
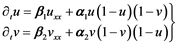 (5)
(5)
where in above Equation (5), 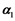 and
and  are the linear growth rate whereas
are the linear growth rate whereas 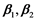 are coefficients of the diffusion [3] [4] [5] , with
are coefficients of the diffusion [3] [4] [5] , with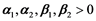 , as well as
, as well as 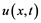 and
and ![]() are the concentrations of the chemicals in the reaction diffusion process.
are the concentrations of the chemicals in the reaction diffusion process.
3. Exact Solution
Exact solution to system in Equation (5) found by E. S. Fahmy [5] , he used factorization method, given below:
![]() (6)
(6)
![]() (7)
(7)
4. Smoothness and Uniqueness of the Reaction Diffusion System
It is very important to enforce some assumptions on some physical parameters or related reaction functions, to analysed the smoothness and uniqueness of a positive oriented natural solution by considering lower and upper bound of the solution of the system which mentioned in Equation (5) [6] . We assume that ![]() which represents the diffusion coefficients are always positive in the bounded or finite domain such as
which represents the diffusion coefficients are always positive in the bounded or finite domain such as![]() , whereas initially means at
, whereas initially means at ![]() the un- knowns such as
the un- knowns such as ![]() are non-negative [6] . The smoothness hypothesis is used to guarantee the existence of the problem of the corresponding linear system [6] . Let us look at the complete obtained system in one dimension,
are non-negative [6] . The smoothness hypothesis is used to guarantee the existence of the problem of the corresponding linear system [6] . Let us look at the complete obtained system in one dimension,
![]() (8)
(8)
imposed the following boundary conditions on Equation (8), which is,
![]() (9)
(9)
imposed the following initial conditions on Equation (8), which is,
![]() (10)
(10)
combined above three equations, to get the model system.
Assumption or Hypothesis (H)
Let us suppose that ![]() exists and is also bounded which is subsets of domain
exists and is also bounded which is subsets of domain ![]() and there exists a function with
and there exists a function with![]() , such that
, such that ![]() for
for ![]() [6] . This definition implies that the function f is monotone non-decreasing in
[6] . This definition implies that the function f is monotone non-decreasing in ![]() and is uniform bounded for
and is uniform bounded for ![]() [6] . Clearly this condition is satisfied by function f [6] . Thus this property leads to
[6] . Clearly this condition is satisfied by function f [6] . Thus this property leads to
![]() (11)
(11)
![]() (12)
(12)
where above Equations (11), (12) represents ![]() are quasi monotone non- increasing and quasi monotone non-decreasing functions in
are quasi monotone non- increasing and quasi monotone non-decreasing functions in ![]() respectively [6] . According to classification of the reaction functions,
respectively [6] . According to classification of the reaction functions, ![]() are typed III functions [6] . This leads to the following definition of the solutions.
are typed III functions [6] . This leads to the following definition of the solutions.
4.1. Definition
A smooth pair of two vector functions![]() ,
, ![]() defined in
defined in ![]() are called upper and lower solutions respectively [6] , if they satisfy the following inequalities
are called upper and lower solutions respectively [6] , if they satisfy the following inequalities
![]() (13)
(13)
In the above definitions the smoothness of![]() ,
, ![]() is in the sense that these functions are continuously differentiable to the order appeared in Equ- ations (8) and (11), (12) respectively [6] . Hypothesis and above definition leads to the following theorem.
is in the sense that these functions are continuously differentiable to the order appeared in Equ- ations (8) and (11), (12) respectively [6] . Hypothesis and above definition leads to the following theorem.
4.2. Theorem
Let f holds hypothesis (H). If there exist upper and lower solutions![]() ,
, ![]() of system (8), with
of system (8), with ![]() and
and ![]() in
in![]() , then the sequence
, then the sequence![]() ,
, ![]() converges monotonically from above and below, respec- tively [6] , to a unique solution (u, v) of system (8) [6] . Moreover,
converges monotonically from above and below, respec- tively [6] , to a unique solution (u, v) of system (8) [6] . Moreover,
![]() (14)
(14)
The quality of being of practical use about above theorem, need to construct of lower and upper solutions, with existence problem to be ensured [6] , but the asymptotic behaviour of the time-dependent solution and related stability can also be established from the behaviour of the lower and upper solutions [6] , ac- cording to the definition, so stability of a steady-state solution make according to selection of Lyapunov function [6] , be that as it may for the global existence problem or the stability problem with homogeneous boundary conditions [6] .
5. Numerical Methods
Let us apply numerical methods technique, to solve such system which men- tioned in Equation (5) in finite domain![]() . We partitioned the interval
. We partitioned the interval ![]() into n equal parts of width h [7] [8] . Place a grid on the rectangle region R by drawing vertical and horizontal lines through the points. Numerical solution is denoted by
into n equal parts of width h [7] [8] . Place a grid on the rectangle region R by drawing vertical and horizontal lines through the points. Numerical solution is denoted by![]() , whereas exact one make in the form of
, whereas exact one make in the form of ![]() respectively.
respectively.
5.1. Forward in Time and Centre in Space (FTCS) Scheme
We consider forward in time and center in space (FTCS) explicit scheme by substituting the forward difference approximation for the time derivative and the central difference approximation for the space derivative in system in Equation (5),
![]() (15)
(15)
![]() (16)
(16)
where![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Finite difference schemes, must pass certain tests of accuracy, consistency, stability and convergence [9] [10] [11] , we discuss these concepts in the follow- ing way.
5.1.1. Accuracy of FTCS
Accuracy of the FTCS scheme for system in Equation (16), we apply Taylor’s series on each term, which is as follows:
![]() (17)
(17)
simplifies above equations, we get the following,
![]() (18)
(18)
dividing above system, by k and simplifies some terms:
![]() (19)
(19)
This leads to principle part of the truncation error (PPTE), which is as follows:
![]() (20)
(20)
which shows that this scheme has 2nd order accuracy in space and first order accuracy in time such as ![]() [9] .
[9] .
5.1.2. Consistency of FTCS
According to the definition of the consistency, if the difference between finite difference equation (FDE) and related partial differential equation (PDE), i.e truncation error vanishes as the sizes of the grid spacing go to zero inde- pendently, i.e
![]() (21)
(21)
Equation (20) is consistent, because the truncation error divided by k tends to zero as h and k tends to zero [11] [12] [13] [14] .
5.1.3. Convergence of FTCS
A finite difference method is convergent if the solution of the finite difference equation approaches to exact solution of the partial differential equation as the sizes of the grid spacing h and k tends to zero [13] [14] [15] .
![]() (22)
(22)
where ![]() is called the discretization error.
is called the discretization error.
![]() (23)
(23)
where ![]() is called the discretization error.
is called the discretization error.
![]() (24)
(24)
![]() (25)
(25)
this completes the proof of the convergence.
5.1.4. Stability of FTCS
Another important feature of a finite difference method of solving partial dif- ferential equation is the stability of the associated finite difference equation which must be investigated. Let us look again Equation (16),
![]() (26)
(26)
linear form of above Equation (26), is as follows:
![]() (27)
(27)
where![]() , from Equations (26) and (27), we can write in the following way,
, from Equations (26) and (27), we can write in the following way,
![]()
where![]() .
.
![]() (28)
(28)
where
![]()
where matrix ![]() is called the amplification matrix. According to Von-Ne- umann stability analysis, the condition for stability for system is
is called the amplification matrix. According to Von-Ne- umann stability analysis, the condition for stability for system is
![]() (29)
(29)
above Inequality (29) leads to the following two special cases,
1) Special Case 1
・ The right hand side of the Inequity (29) gives,
![]() (30)
(30)
which is condition of stability to FTCS scheme in coupled non-linear PDE system.
2) Special Case 2
・ The left hand side of the Inequity (29) gives,
![]() (31)
(31)
which is condition of stability to FTCS scheme in coupled non-linear PDE system.
Special case (1) and special case (2) lead to the following very interesting results,
![]() (32)
(32)
The Von-Neumann stability analysis is the most common used method of de- termining stability criterion as it is generally the easiest to apply. It can only be used to establish a necessary and sufficient condition for stability of linear initial value problems with constant coefficients [14] [15] [16] [17] [18] [19] . Thus according to Von-Neumann stability analysis, FTCS scheme is conditionally stable as obtained in Equation (32).
5.2. Crank Nicolson Implicit Scheme
Let us apply Crank Nicolson implicit finite difference scheme to Equation (5).
![]() (33)
(33)
after some simplification, we get the following,
![]() (34)
(34)
![]() (35)
(35)
combine Equations (34) (35), we get the following,
![]() (36)
(36)
where ![]() and
and ![]() are mentioned in Equation (16).
are mentioned in Equation (16).
5.2.1. Accuracy of CN
Accuracy of the CN scheme to Equation (36), we apply Taylor’s series on each term. After some simplification, resultant is as follows,
![]() (37)
(37)
![]() (38)
(38)
we divide above equation by time step k with using in system (5), to get the accuracy, in the following form,
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
Now principle part of the truncation error (PPTE) is as follows:
![]() (42)
(42)
which shows that this scheme is 2nd order accurate in both time and space, such as ![]() [19] [20] .
[19] [20] .
5.2.2. Consistency of CN
From accuracy, we find principle part of the truncation error along with Equ- ation (42). Which shows that Crank Nicolson scheme is consistent because ![]() tends to zero as h and k tends to zero, i.e.
tends to zero as h and k tends to zero, i.e. ![]() as
as![]() .
.
5.2.3. Stability of CN
Stability of the associated finite difference Equation (36), which is in linear form,
![]() (43)
(43)
where ![]() and
and ![]() are mentioned in Equation (16) and Equation (27) re- spectively. From Equation (43), we can write,
are mentioned in Equation (16) and Equation (27) re- spectively. From Equation (43), we can write,
![]()
where ![]() and
and![]() .
.
According to Von-Neumann stability analysis, we have
![]() (44)
(44)
where
![]()
where matrix ![]() is called the amplification matrix. According to Von-Neu- mann stability analysis (29). We have
is called the amplification matrix. According to Von-Neu- mann stability analysis (29). We have
![]() (45)
(45)
![]() (46)
(46)
Above Equation (46), satisfies the Von-Neumann stability criterion, which shows that CN scheme for Equation (5) is unconditionally stable [21] [22] [23] [24] [25] .
5.3. Fourth Order Accurate Implicit Scheme
Let us apply another implicit scheme with improved accuracy in space to Equation (5).
![]() (47)
(47)
![]() (48)
(48)
where![]() , and
, and ![]() are mentioned in Equation (16).
are mentioned in Equation (16).
![]() (49)
(49)
![]() (50)
(50)
combine Equations (49) (50), to get the following,
![]() (51)
(51)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]()
5.3.1. Accuracy of Douglas Scheme
Accuracy of the Douglas scheme to Equation (36), we apply Taylor’s series on each term. After some simplification, resultant is as follows,
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
Dividing above Equations (54) and (55) by k and take into account Equation (5), so resultants are as follows:
![]() (56)
(56)
let us look above equation in new way,
![]() (57)
(57)
Now principle part of the truncation error (PPTE) is as follows:
![]() (58)
(58)
which shows that this scheme is 4th order accurate in space, such as ![]() [26] [27] [28] [29] [30] .
[26] [27] [28] [29] [30] .
5.3.2. Consistency of Douglas Scheme
From accuracy, we find principle part of the truncation error along with Equ- ation (58). Which shows that Douglas scheme is consistent because ![]() tends to zero as h and k tends to zero, i.e.
tends to zero as h and k tends to zero, i.e. ![]() as
as ![]() [31] [32] .
[31] [32] .
5.3.3. Stability of Douglas Scheme
Stability of the associated finite difference Equation (51), which is in linear form, is
![]() (59)
(59)
![]() (60)
(60)
Consider Equations (44) (60), in the following few important steps.
![]() (61)
(61)
Apply Von-Neumann stability analysis to Equation (60), we get the following
![]() (62)
(62)
![]() (63)
(63)
Above Equation (63), satisfies the Von-Neumann stability criterion, which shows that fourth order implicit scheme is unconditionally stable [33] [34] [35] [36] [37] .
5.4. Richardson Extrapolation Technique
Richardson extrapolation method lead to considerable improvement of numerical results which solving the partial differential equation system by finite difference method. Richardson’s extrapolation formulae are [38] [39] ,
![]() (64)
(64)
above formula leads to get fourth order accuracy [39] [40] ,
![]() (65)
(65)
6. Error Norms
The aim of the accuracy is assessed by some redefined norms, associated with the consistency of the finite difference schemes, such scaled measurement to error defined in term of norms specially ![]() and
and![]() , which are outlined below:
, which are outlined below:
![]() (66)
(66)
![]() (67)
(67)
![]() (68)
(68)
![]() (69)
(69)
![]() (70)
(70)
where ![]() and
and ![]() are errors in
are errors in ![]() and
and ![]() at number of partitions h and h/2 respectively [41] [42] .
at number of partitions h and h/2 respectively [41] [42] .
7. Results
Numerical computations have been performed using the uniform grid [14] [21] [25] [29] . For the test problem (5), we analysed results with various finite difference schemes. In Tables 1-3, we fixed domain as ![]() with k = 0.0001 and find results at
with k = 0.0001 and find results at![]() . In these three tables, we obtain insight error. Table 4 and Table 5 show results for
. In these three tables, we obtain insight error. Table 4 and Table 5 show results for ![]() and
and ![]() norms for major
norms for major
![]()
Table 5. Estimates of results, with two different Implicit FD schemes. Relative error values give encouragement to our results. Fixed some parameters as![]() , k = 0.0001 and h according to grid with wave speed c = 2 and z = 1.
, k = 0.0001 and h according to grid with wave speed c = 2 and z = 1.
schemes CN and Douglas at different grids and time levels. Rate of convergence is defined in Table 6. All these six tables show results for three implicit scheme to analyse error and performance of the schemes. According to results men- tioned in tables, these scheme play very important role for convergence although non-linear system is difficult to stabilized. In Figure 1, FTCS conditionally stable finite difference scheme is used at different grid, also we did in Figure 2 with Crank Nicolson implicit scheme. Fixed some parameters in CN scheme to get common region at different time level, as we mentioned in Figure 3. In Figure 4 and Figure 5, we did comparison of results with two different schemes at various time levels. In Figure 6 and Figure 7 attractive common region at different time level is obtained. In Figures 8-10, comparison of results with Richardson, Douglas and exact in ![]() component and
component and ![]() form. Last Figure 11 is obtained at
form. Last Figure 11 is obtained at ![]() form of results with two finite difference schemes. From Tables and Figures, we observed that these schemes exactly predict accuracy as we learn from literature reviews.
form of results with two finite difference schemes. From Tables and Figures, we observed that these schemes exactly predict accuracy as we learn from literature reviews.
8. Conclusions
In this chapter, the solution to one dimensional coupled Fisher KPP system is successfully approximated by a various numerical finite difference schemes. Explicit FTCS is conditionally stable, and we give more attention to parameter R1 and R2, which can be used to stabilized the results as we can see from Figure 1. Crank Nicolson and Douglas schemes are implicit schemes with uncondi- tionally stable nature, this guarantee is given by Von-Neumann stability analysis
![]()
Table 6. Estimates the rate of convergence for two implicit FD schemes for different grids.
![]()
Figure 1. Shows results using FTCS scheme at two different grids, keeping the conditionally stable term. Area under the curves is the common region for two different grids.
![]()
Figure 2. Shows results using Crank Nicolson scheme at two different grids.
![]()
Figure 3. Shows results using Crank Nicolson scheme at two different time level. Common region is the wave front that we study in literature [35] [39] [41] .
![]()
Figure 4. Shows results using Crank Nicolson scheme at various time levels. We did comparison with exact solution for ![]() and
and ![]() components.
components.
![]()
Figure 5. Shows results using fourth order implicit scheme at various time levels. We did comparison with exact solution for ![]() and
and ![]() components.
components.
![]()
Figure 6. Shows fourth order implicit scheme at three different time level. Common region is the wave front that we study in literature [17] [23] [29] [41] .
![]()
Figure 7. Shows results using fourth order implicit scheme at various time levels, with common region.
![]()
Figure 8. Shows results using Richardson Extrapolation and fourth order implicit scheme, with comparison to exact solution for u component.
![]()
Figure 9. Shows results using Richardson Extrapolation and fourth order implicit scheme, with comparison to exact solution for ![]() form.
form.
![]()
Figure 10. Shows results using Richardson Extrapolation at different time levels, along fourth order implicit scheme.
![]()
Figure 11. Shows a comparison of two schemes in u(x,t)/v(x,t) form, with exact solution.
as we explained in methodology section [27] [28] [29] [31] [35] [36] . Jacobean found with the help of Newton’s iterative method [36] [38] , whereas tridiagonal nature of the linear obtained system is solved by Crout’s or Partially Pivoting method. These method are highly computable in term of non-linear system as we defined in this chapter [40] [41] [42] . Numerical results show great deal of match- ability to exact solution. Accuracy in results are glanced from figures and tables.
Acknowledgements
Shahid Hasnain, Prof. Daoud Mashat and Muhammad Saqib is thankful to Dr Muhammad Faheem Afzaal, Department of Chemical Engineering, Imperial College London and Vineet K. Srivastava, Scientist, ISTRAC/ISRO, Bangalore, India for thoughtful remarks. This research was supported by Department of Mathematics, division of Numerical Analysis, King Abdulaziz University, Jeddah, Saudi Arabia.
Conflict of Interest
There is no conflict of interest in this research paper.