Universality of Periodic Oscillation Induced in Side Branch of a T-Junction in Numerical Simulation ()
1. Introduction
T-junction is a typical fluid pipe element used in the construction of power plants. Over the past three decades, many experimental and numerical researchers have investigated laminar flow inside T-junction for relevance in hemodynamics [1] [2] [3] [4] .
More recently, the focus in the hemodynamics field has been the flow instabilities induced in a cerebral aneurysm from the perspective of their growth and rupture [5] [6] [7] . Indeed, although the flow instability and the turbulence occur around the cerebral aneurysm, this instability appears in a pulsatile flow, i.e. unsteady flow in a proximal vessel. Furthermore, this phenomenon disappears in a distal vessel. The flow instability also appears in the nasal channel and cantilevered flexible plate [8] [9] [10] . However, this flow instability has not necessarily led to strong periodic oscillations; they may appear temporarily and sometimes as weak periodic oscillations.
Brown & Roshko [11] and Tani [12] found that when two parallel flows differing velocity merge, the high-shear-rates at the interface of these flows induce Kelvin-Helmholtz flow instability and that this phenomenon is universal. These findings are based on fluidoscillation and vibration occurring in the dynamics of fluid flows. Oscillations, self-sustaining oscillations and instability have been studied experimentally for flow past a cavity [13] [14] , and flow through an axisymmetric stenosed channel [15] .
In previous studies of the T-junction [16] [17] [18] [19] , we found that a periodic oscillation was induced in the side branch and that the Strouhal number based on variables in the side branch was independent of Reynolds number, flow division ratio and the ratio of the radii of the side branch and trunk. Qualitatively, this implies that at a certain cross-section the oscillation is strongly related to the local flow structure, i.e. high-shear-rate flow between two pairs of vortices with the same rotational sense in the cross section immediately downstream of the side branch. Furthermore, in addition to high-shear-rate flow between two vortices, a fluid oscillation is induced along the shearing separation layer where the tangential velocity profile has inflection points with shear rate several orders larger than that further downstream [19] . Subsequently, the mechanism for the flow vibration was clarified from the flow instability of two kinds of high-shear-rate flow with the inflection point in the side branch of the T-junction confirming the universality of the phenomenon.
However, the experimental approach was unable to clarify in detail how the mechanism of the periodic oscillation occurs, i.e. the spatial amplification of flow instability and the distribution of wall shear stress (WSS). In the present study, this mechanism is clarified numerically. The mechanism of periodic oscillation induced in the side branch obtained in the experiment was verified in numerical simulation.
2. Method
Numerical simulations were performed of flow in a T-junction (Figure 1) configured with the same setup as studied in a previous experimental study [18] . The side branch bifurcates at right-angle from the trunk. To examine the
universality of the independency for the Strouhal number, a typical setting employed a Reynolds number of ReS = 700 (QS/QT = 0.50) in the side branch corresponding to ReT = 800 in the trunk. Also, the tube radius ratio and the flow division ratio were fixed at RS/RT = 0.57 and QS/QT = 0.25, 0.33 and 0.5 [18] , respectively. The flow division ratio is primarily at QS/QT = 0.5 because the oscillation frequency is clear at this condition in experiment. Furthermore, in numerical calculation, we examined the spatial amplification of velocity due to flow instability and the distribution of wall shear stress.
The velocity components at 480 numerical grid points in the upper half plane (grid B in Table 1) were interpolated from 129 measurement data on a non-uniformly spaced rectangular grid in the Y-Z plane. The velocity vector field experimentally obtained for a Cartesian coordinate system (Figure 2(a)) in a previous study is given as the upstream boundary condition [S3 in Figure 3(a)] [18] , where is furthest upstream measurement location for the laser Doppler anemometry. As cylindrical coordinate system is used in the simulation, the velocity in Figure 3(b) was interpolated from several points in the Cartesian coordinate system using a staggered grid near the point (Figure 2(b)). Specifically, as a grid of cylindrical coordinate in Figure 2(b) does not coincide with that of Cartesian coordinate, the velocity component Φ at a grid point in cylindrical coordinate using the following equation is interpolated from the surrounding velocities ϕi in Cartesian coordinate.
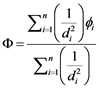 (1)
(1)
where di is each distance from the grid in cylindrical coordinate to the surrounding grids in Cartesian coordinate. The numerical domain is L = 0.046 m,
![]() (a)
(a) ![]() (b)
(b)
Figure 2. (a) Cylindrical and Cartesian grid; (b) Interpolation to simulation data from experiment.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 3. Inlet condition and shearing flow at section S3. (a) Measured secondary velocity vector plots (upper semicircle) and iso-axial velocity contours (lower semicircle) [18] ; (b) Interpolated secondary velocity plots (left) and iso-axial velocity contours (right); (c) Oscillation range in upstream boundary condition.
i.e. X/RS = 2.89 - 9.46.
3. Simulation
A cylindrical coordinate system (r, θ, z) was specified for the side branch (Figure 1) with corresponding velocity components (u, v, w). The governing equations for the incompressible viscous fluid flow are the Navier Stokes equations,
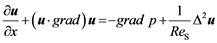 (2)
(2)
and the continuity equation,
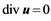 (3)
(3)
where the dimensional variables (u, v, w), (r, θ, z) and (X, Y, Z) are normalized using mean velocity US = 8 ´ 10−2 m/s and radius of RS = 7 ´ 10−3 m in the side branch. Here, the kinematic viscosity and the density of the working fluid are ν = 1.58 ´ 10−6 m2/s and ρ = 1830 kg/m3, respectively.
In the following numerical simulation, the steady flow is first obtained, and then an unsteady flow simulation was performed with the upstream boundary condition, in which the velocity field rotates around the axis of the side branch with a small angle around the axis of the side branch.
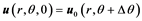 (4)
(4)
As depicted in Figure 3(c), the upstream boundary condition describes periodic oscillations with small angular variation,
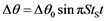 (5)
(5)
The amplitude of the rotation angle Δθ0 is set to π/180 (1˚), and the frequency equals the empirical value observed in the experiment, StS = 1.03 (f = 6 Hz) [18] . A time-dependent simulation was performed with the initial condition of the previous steady flow result until a steady oscillating flow was obtained.
The free-stream condition is applied at the downstream boundary. Thus, the flow instability in the side branch was generated numerically as follows. The time-dependent simulation was performed with the initial condition until a steady oscillating flow was obtained.
The discretized representations of the relevant equations were obtained through the control volume method, and solved using an iterative algorithm employed in the original code similar to SIMPLER method developed by Patanker [20] . The features of the present solution procedure [21] are summarized as follows. The convective derivative terms are discretized through the consistently reformed QUICK scheme, which guarantees continuity of momentum flux during each iteration and significantly improves numerical stability [22] . The modified strongly implicit procedure of Schneider and Zedan is employed to solve the linearized penta-diagonal matrix equations [23] . In discretizing the local derivative term, the second-order accurate three-time-level scheme is employed [24] .
The numerical settings are listed in Table 1. Parameter values for grid A such as the grid spacing and the length of the computational domain are determined from a preliminary simulation using grid B. The numerical simulations were carried out for both grids A and B. The criterion for each velocity is the convergence ε. Comparing of the amplification degree in grid A with that in grid B as described below, there is little difference between grid A and grid B. So, we primarily carried out to simulate in grid A with coarse mesh and uniform grid.
The amplification degree is defined as the ratio of (Urms)max within X/RS = 2.89 − 9.46 to (Urms)0 at the section S3 as follows,
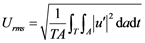 (6)
(6)
where T and A are period and cross sectional area of side branch, respectively. When various frequencies, specifically, 0.1 Hz and 1 Hz to 12 Hz in steps of 1Hz, were set for the perturbation at the upstream boundary section, the degree of amplification in the spatial change of axial velocity across each cross section examined downstream in the side branch depended on the given frequency. When the ratio of the amplification degree (Urms)maxof at each section to (Urms)0 at section S3 converged within 5% of the maximum amplification degree found under various frequencies as described above, the given frequency was regarded to be reasonable. This is the major criterion for the convergence in the present numerical simulation.
4. Results and Discussion
A time dependent simulation was performed with a null velocity field as an initial condition. After the transient flow diminished, the flow solution converged onto a steady state, i.e. the flow oscillation appearing in experiments was not reproduced in this simulation. The fixed upstream velocity boundary condition has probably stabilized the flow in the side branch. For this reason, the effect of a small perturbation given in (4) was examined in relation to the stability of the flow field.
Under the periodic oscillations imposed on the upstream boundary condition as described above, the oscillation in the axial velocity component at the off-axis point (X/RS, Z/RS) = (0, 0.25) for three axial sections S3, S5 and S7 (X/RS = 2.89, 4.32, 5.75) was shown in Figure 4(a) and Figure 4(b). This instant at t = 12.7 corresponds when the oscillation of the axial velocity at the point is a minimum. It is sure that the velocity change, i.e. amplitude, is small in section S3 and a little large in section S5. It becomes much larger in section S7. Further downstream of section S7, the amplification attenuates asymptotically. Thus, the spatial amplification and section of velocity relates to the flow instability. The small periodic oscillation given at the upstream boundary S3 is substantially amplified at the downstream location S7 with a phase lag of 0.21π rad which is calculated from the time difference Δt = 0.2, i.e. t = 12.7 and t = 12.9, of the minimum velocity in sections S3 and S7, respectively. As one period is 1.9, the phase lag is 2π × 0.2/1.9 = 0.21π. This one period of 1.9 corresponds to the periodic frequency of f = 6.00 Hz, i.e. StS = 1.05, which agrees well with the experimental results of 1.03 [18] .
Contours plots of the secondary velocity vector and the iso-axial velocity contours at the downstream sections S5 and S7 (X/RS = 4.32 and 5.75) at t = 12.7 (Figure 5) show a pair of small vortices in the downstream section S5 (X/RS = 4.32), which are also seen in the upstream boundary, moving toward the near wall while another pair of slightly stronger vortices grew larger; the iso-axial velocity contours are a little asymmetric. Section S7(X/RS = 5.75) further downstream features two pairs of small and large vortices merging to form one pair of large vortices. Significant asymmetry is indicated in the axial velocity distribution; also, the iso-axial velocity contour is asymmetric because of flow instability, i.e. the small periodic velocity oscillation introduced in the upstream boundary has amplified downstream. The current simulation results at the sections S5 and S7 qualitatively agree with the experimental results (Figure 6), respectively [19] although the secondary velocity of the experimental result is a little bigger than the numerical result. Simultaneously, the flow instability was induced along the shearing separation layer (see Figure7) at X/RS = 3.17 immediately downstream
![]() (a)
(a) ![]() (b)
(b)
Figure 4. Time variation of axial velocity in sections S3, S5 and S7 at representative point (Y/RS = 0.0, Z/RS = 0.25). (a) Axial velocity in sections S3, S5 and S7; (b) Magnified axial velocity in section S3.
![]() (a)
(a)![]() (b)
(b)
Figure 5. Secondary velocity vector plots and iso-axial velocity contours at t = 12.7. (a) Section S5; (b) Section S7.
![]()
![]()
Figure 6. Secondary velocity vector measured in PIV [18] . Left and right sides denote at sections S5 and S7, respectively.
![]()
Figure 7. Tangential velocity profile across shearing separation layer at section X/RS = 3.17 (Shear rate downstream of side branch = 47 s−1) [19] .
from section S3 [19] . The shear-rate (296 s−1) at this layer is 6 times larger than that (47 s−1) at the tube wall downstream of the side branch; the tangential velocity profile indicates a clear inflection point. This is one feature associated with the flow instability in the side branch of T-junction, which is one kind of Kelvin-Helmholtz instabilities. In the upper half of Figure 3(a) and Figure 3(b), there exist two counter-clockwise vortices, which generate a small vortex at the near wall and a little strengthening large vortex with the same rotational sense. Therefore, the high-shear-rate at the interface between these two vortices is another feature of this flow instability. Two pairs of vortex in the experiment look like those in curved bend [25] [26] . However, two pairs of vortex in the present result as shown in Figure 3(a) is fundamentally different from those in the curved bend, which these vortices rotate without same rotational sense and hence there is no friction at the interface between each vortex.
The range of Strouhal number StS, i.e. oscillating frequency, in the present simulation approximately agrees with that obtained in experiment (Figure 8) in the range of StS = 0.9 - 1.1, although there is a little deviation between the simulation and the experiment. Indeed, the observed oscillation depends on the amplification of flow instability in the side branch.
The time average WSS τuw in the distal wall in Figure 9(a) is much larger than that in the near wall; moreover, WSS τuw in the section S3 is globally larger than that in the downstream region. The root mean square (RMS) of WSS τuw-rms = 0.9 at X/RS = 8.5 in the downstream region as shown in Figure 9(b) is much higher than that of 0.2 at X/RS = 3.2 downstream of section S3. This difference in τuw-rms is closely related to the flow instability that is amplified in the downstream region. Furthermore, the amplitude of the resultant WSS τuw-amp = 1.75 at the near wall X/RS = 6.5 denoted by A and τuw-amp = 2.50 at the distal wall X/RS = 8.5 denoted by B are large in Figure 9(c).
5. Conclusion
The mechanism for flow instability in the side branch of a T-Junction in steady laminar flow was clarified using a periodic velocity perturbation introduced as
![]()
Figure 8. Reynolds number ReS, versus, Strouhal number StS.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 9. Contours of time average, RMS and amplitude of resultant WSS τuw. (a) Time average of WSS; (b) RMS of WSS; (c) Amplitude of resultant WSS.
an upstream boundary condition in a numerical simulation. The simulation result qualitatively agrees with experimental measurements. The spatial amplification accompanied with the flow instability in the side branch by numerical simulation explains the occurrence of the velocity oscillation observed in the experiment. Therefore, this periodic oscillation motion is a universal phenomenon in the side branch of a T-junction.
Acknowledgements
The authors thank Mr. Takashi Fujiwarain Chiba University for suggestions concerning data processing.
In this study, the authors cited Figure 3(a) from Yamaguchi, R. et al., “Variation of Wall Shear Stress and Periodic Oscillations Induced in the Right-Angle Branch during Laminar Steady Flow”, 127 (2005) [18] and Figure 6 and Figure 7 from Tanaka, G. et al., “Fluid Vibration Induced by High-Shear-Rate Flow in a T-Junction”, 138 (2016) [19] published by ASME J. Fluids Eng., after getting the permission of copyright.
The authors declare no conflicts of interest.
Nomenclature
f: frequency of fluid vibration
L: streamwise length of simulation domain
n: coordinate normal to shearing separation layer
QS: flow rate through side branch
QT: flow rate through trunk
q: tangential velocity along shearing separation layer
ReS = 2RSUS/ν: Reynolds number based on variables of side branch
ReT = 2RTUT/ν: Reynolds number based on variables of trunk
RS: radius of side branch= 7 mm
RT: radius of trunk= 12.25 mm
(r, θ, z): cylindrical coordinate defined in side branch
StS = 2fRS/US: Strouhal number based on variables of side branch
t= t*/(RS/US): dimensionless time
t*: dimensional time
Urms: root mean square root of axial velocity
(Urms)0: root mean square root of axial velocity at section S3
US: mean velocity in side branch
UT: mean velocity in trunk
(u, ν, w): velocity component in (r, θ, z) coordinate direction, respectively
(u', ν', w'): velocity fluctuation of each velocity
(X, Y, Z): Cartesian coordinate defined in the whole right angle branch
τuw: non-dimensional resultant wall shear stress [= τuw*/(4ρνUT/RT)]
![]() : dimensional resultant wall shear stress
: dimensional resultant wall shear stress
ν: kinematic viscosity of working fluid
ρ: density of working fluid