Matlab Code to Assess the Reliability of the Smart Power Distribution System Using Monte Carlo Simulation ()
1. Introduction
The application of Monte Carlo simulation (MCS) is a corner-stone in the sensitivity and quantitative probabilistic analysis. Among many of its great virtues is its powerful ability to accurately evaluate the reliability of the electrical grid, which allowed several studies to emerge in this arena. The deterministic approach in assessing the reliability of the power systems is criticized for not being sensitive to the stochastic nature of the grid as well as to customer demands and components failures, which may lead to either an overinvestment or catastrophic consequences. Therefore, the need for probabilistic evaluation of the electrical system behavior has been emphasized in the most recent decade. MCS, as a process of simulation, is strictly random and can be divided into two main types; sequential and non-sequential (random) Monte Carlo methods. The sequential MCS simulates the system operation as an up-and-down, where a system operating cycle is obtained by combining all the cycles of the system components in chronological order. This usually requires more computational efforts than the other approach, the non-sequential MCS, which simulates the system with a higher efficiency by choosing intervals randomly, yet cannot simulate the chronological aspect of the system behavior. The MCS process is central in the stochastic simulation using random variables, where it can simulate the electrical components considering the grid’s behavior with the goal of evaluating its expected reliability parameters [1] [2] . It also provides distribution information for the load point indices, system indices, and the energy not served costs [3] [4] .
The goal of this work is to apply the Monte Carlo technique on the IEEE 34-node test system, shown in Figure 1, to evaluate the reliability of the distribution network using the applications of the smart grid concept considering different case scenarios. Specifically, we consider the impact of the automatic reclosers (ARs) as well as the distributed generators on the system with the optimal placement of the ARs on the feeder, as MCS helps in building an artificial history for each component operation for a simulation time, which was set in this work to be 2000 years. The work aims to compare the results obtained using MCS with results obtained previously for the same test system using another approach [5] . The work also seeks to produce a sufficient MATLAB code that can be used to perform MCS analysis and provide the famous reliability indices SAIDI, SAIFI, CAIDI, EUE, and ASAI for any study-scale electrical test systems. The results should reflect the definition of the smart grid that identifies the ability of a sys- tem for a self-healing, self-interrupting of faults [6] . Reference [7] shows diffe-
rent emerging technologies of the auto-reclosers that are now available in the industry.
2. Monte Carlo Study
2.1. Concept of MCS
A Monte Carlo Simulation’s Matlab code was developed at the University of Southern California by the authors of this paper to achieve the purpose of this study. The code can be found in Appendix of this work. The input data utilized in this work represents a real system data taken from reference [1] , which was also used in the reliability study done by the authors in [5] . The distribution system reliability in overall is evaluated using load point indices and system indices, which are the average failure rate (λi), average outage time (r), and the average annual unavailability (U). The method considered in the coding is the time-se- quential MCS, which models the system recognizing the chronological order as the incidents occur on the system through the simulation time. An artificial history is generated using the random number generator which produces a uniform random number (between 0 and 1) for each component in the test system for the goal of providing a sequence of the operating-repairing cycle for it.
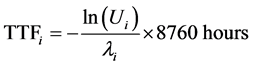
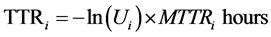
We simulated the IEEE test system using the famous two-state Markov model shown in Figure 2 for all the non-source components in the feeder. The process is highly random in nature as we do not know for sure when, where and which component in the system will fail first with the fact that the behavior will be different from one component to another, including the type and number of failures as well as the time between a failure and restoration of a component. This fact contributes to the virtue of MCS as a powerful tool to model these real behavior patterns in a simulated time for the sake of producing average reliability values for a system when considering major design changes, such the integration of smart grid technologies in its infrastructure. The Markov model has two states; either up which for the operating condition of the components, or down for the failing state. The up-state is also referred as TTF (time-to-fail) while the down-state referred as TTR (time-to-repair/replace). It is noted that both TTR and TTF are random in nature. The process from up to down is known as the
![]()
Figure 2. The two-state model of a component.
failure process for a component due to contingency event that would take it out of operation. MCS randomly sample the up and down states for each element in the feeder which generates a simulated sequence for the component’s history of operation and failure. This helps in producing an overall conclusion about the system behavior in general, and to identify the component that is prone to outages in particular. Figure 3 illustrates the concept of TTR and TTF for a component in any system. These times can be represented by random variables and simulated using gamma, exponential, normal, lognormal and Poisson distributions [7] [8] .
2.2. MCS Simulation Process
1) Generate a random value for each of the component using the random number generator. The variable obtained for each component take the value between (0, 1) with equal likelihood.
2) Determine the component in the grid with the minimum TTF.
3) Convert the generated values into TTF, TTR for each component in the system. Determine the outage duration for each failed load point indices.
4) Generate a new random number for the failed component and convert it into a new TTF. If the simulation time is less than a year then return to step 2. Otherwise, go to step 7.
5) Calculate the number and duration of failures for each load point per year.
6) Calculate the average value of the load point failure rate and duration for the sample years.
7) Calculate SAIDI, SAIFI and system indices and record the average values of the results.
8) Return to step 2 if the simulation time is less than the specified total simulation years. Otherwise, record the results as final outcomes and end the simulation.
3. Modeling the Test System in Matlab Considering Smart Grid Technologies
3.1. Case 1(A): Installation of One Automatic Recloser (AR) in the Feeder
The results of modeling the test system in our MATLAB code are provided in Table 1. The application of the smart grid technologies on the reliability of the
![]()
Figure 3. The operating/failure time of a component.
![]()
Table 1. Results of installing one automatic recloser to the test system.
distribution feeder is weighed based on the outcomes (of using the sequential Monte Carlo) that show the impact of the smart grid applications (the auto- recloser in this case) versus the conventional (main) scheme of the test system in Figure 1. As shown in Figure 4, the installation of an automatic recloser will yield a reduction in both SAIDI and SAIFI as to the scenario of having the regular system. The best improvement is when we consider this automatic recloser to be installed between nodes 832 - 858 in the electrical feeder, where we noticed a 13.82% improvement in SAIDI [from 6.80 to 5.89 hours/year], 15.76% for SAIFI [from 15.23 to 12.83 occurrence/year] and 13.64% for EUE [from 10,709 to 9248 kW/year]. The improvement in the reliability indices is a result of the fact that the auto-recloser would have the virtue of isolating the fault and restore the service to the healthy parts of the feeder, which also contribute to the quick identification of the faulted area which eventually reduces the repair hours. These two factors significantly improve the reliability indices overall and save much of energy, money, and efforts to the utilities.
Figure 4 shows the impact of the installation of one automatic recloser on the test feeder considering different scenarios and locations, while Figure 5 shows a line graph for the reduction in energy not served index per each option considered. By making a comparison between the results obtained from the analytical method and brute force in the study done by the authors in [5] , and the ones obtained using this MCS MATLAB code, we find a very close effect for the installation of the automatic recloser in each option provided in the table. For example, we notice that there is 4.5% difference in the obtained SAIDI in both studies; the analytical method provided us with 9.32% reductions while MCS show a 13.82% for installing the automatic sectionalizing device between nodes 832 - 858 particularly. The difference in percentage goes little higher in SAIFI but still under acceptable margins, where there is a difference of 7% only in the two studies. The same also applies for EUE, which its concept was obtained mainly from the Lawrence Berkeley National laboratory [10] , where there is only a 4.3% difference between the percentages of improvement in both techniques. These results tell us that both methods are efficient and provided similar outcomes regarding evaluating the reliability of the given system after applying the smart grid applications.
![]()
Figure 4. SAIFI and SAIDI results for case 1(A).
3.2. Case 1(B): Installation of Two-Automatic Recloser (AR) in the Feeder
We want to examine in our work the effect of the installation of two automatic reclosers and try to identify if such move will yield more improvement and cost savings. In this case study, we modified the test system to include an automatic recloser in between nodes 832 - 858, and then model the modified system to investigate any further improvements in the reliability indices if we want to add another AR in the test system. Table 2 shows the obtained results for this case study, with the reliability indices for each scenario when we model using the MATLAB code that we built for the purpose of our work. The best option clearly is to install the second AR in between 834 - 860, where this option will yield in 21.85% improvement in SAIDI from the base case where no ARs are considered. Also in this option, SAIFI witness 22.06% decrease from the baseline scenario. This significant reduction in the interruption/year is contributed to the system’s ability to isolate the faulted area of the feeder once an outage occurs, and be able to restore service and maintain it for the healthy part of the feeder. The virtues
![]()
Table 2. The results of modeling the test system with two ARs.
of modeling the system using MCS is its ability to offer the best location for the ARs considering the artificial data it made for each component of up and down history. Figure 6 shows the results of different scenarios for the installation of a second AR using our MCS MATLAB code, comparing them with the baseline case of having no AR at all in the system.
3.3. Case 2: Installation of 1 MW DG Unit on the Feeder
The best option will be the installation of one automatic recloser between nodes 852 - 832 will improve SAIDI by 60.15%, a change from 6.80 to 2.71 hours/year. SAIFI will experience a great reduction as well from 15.23 to 6.07 occurrence/year, accounting around 60% in improvement as well. In the case of any contingency event, the DG unit will provide the system the ability to operate as a small microgrid, providing service to the unaffected parts of the feeder and improving the system indices. It is worth mentioning that the results using MCS show similar reduction percentage for SAIDI when modeling the same system using the analytical technique and the software that is based on brute force me-
![]()
Figure 6. SAIFI and SAIDI for case TWO ARs.
![]()
Figure 7. SAIFI and SAIDI for 1 MW DG unit.
![]()
Figure 8. EUE index when considering 1 MW DG unit.
![]()
Table 3. Results obtained for installing 1MW DG unit.
thod, where there less than 6% in the difference between the reliability indices in the two studies.
4. Conclusions
Monte Carlo technique is one of the most powerful, efficient methods to evaluate the reliability of the power distribution grids. In this work, we simulate the IEEE 34 node test system using the MSC technique, through a MATLAB code that was written by the authors of this paper and shown in Appendix A of this work. After modeled the IEEE feeder, shown in Figure 1, we made a comparison with a previous study done on the same system but with using another approach. Based on the results, we found that the MCS provided similar results with those obtained using analytical technique [5] and DISREL, an intelligent based program that builds on the brute force concept. The study using the developed MCS MATLAB code shows the impact of the smart grid technologies in improving the reliability indices of the test feeder.
The study shows different scenarios of applying the auto reclosers and the DG units in various parts of the feeder. Furthermore, the automatic reclosers, once installed optimally in the grid as proposed by the software, significantly improve the reliability of the power distribution network by isolating the healthy parts of the system automatically, which maintain the service to a substantial number of customers and reduce the repair time. The distributed generators, although dated back to the late 1970’s, are now considered to be one of the applications that define the smart grid concept. The results of integrating them in the distribution feeder show the advantages of using reliable, assumed dispatchable, DG units near load center. Along with the installation of the automatic recloser, the DGs provide the opportunity of operating the distribution grid as a microgrid, allowing service to continue to parts in the network, something will be greatly admired especially during major outages and blackouts. Also, the study provided in this work shows the amount of energy (in kW) that is saved for the utility in this real life test feeder, through the EUE index which measures the reduction in the energy-not-served for each case option. Also, the comparison of these results with that one obtained previously on the same test feeder using the same real-life inputs shows the MCS MATLAB code we developed is effective, and serves as a tool that can be used in evaluating the reliability of distribution feeders when applying small modifications only. That reflects the difference from the test system used in this study.
Appendix: The Developed Matlab Monte Carlo Simulation Code
clear;
N = 33; % number of components
lambda = [0.3979; 0.8209; 0.7666; 0.1206; 0.8577; ...
0.2586; 0.7049; 0.2429; 0.3521; 0.8118; ...
0.1850; 0.5135; 0.3920; 0.7194; 0.6776; ...
0.2065; 0.3197; 0.3226; 0.8566; 0.3348; ...
0.8950; 0.8833; 0.6400; 0.0412; 0.0518; ...
0.9458; 0.2257; 0.7303; 0.2191; 0.0101; ...
0.7205; 0.1289; 0.1327];
MTTR = [0.3546; 0.6970; 0.8490; 0.8724; 0.0411; ...
0.2098; 0.7382; 0.7379; 0.1978; 0.4534; ...
0.2299; 0.0704; 0.3979; 0.8555; 0.6809; ...
0.2954; 0.8536; 0.7195; 0.3405; 0.0495; ...
0.0174; 0.7846; 0.2554; 0.6597; 0.8496; ...
0.2965; 0.2238; 0.0066; 0.0684; 0.4306; ...
0.7953; 0.7759; 0.9673];
power = [0 55 0 16 0 0 0 5 34 0 0 4 40 7 45 15 146 82 ...
0 67 9 405 45 83 0 0 4 0 32 0 28 2 0 450];
users = ceil(power/2)-1;
%% failure history
duration = 1000; % years
interuption = 0;
outage_time = 0;
maxT = 0;
for i = 1:N
[downT{i},upT{i}] = failure_history2(lambda(i),MTTR(i),duration);
cur = max(upT{i}(1:end));
if (maxT < cur)
maxT = cur;
end
interuption = interruption + length(downT{i})-1;
outage_time = outage_time + sum(upT{i}-downT{i});
% figure;
line(1:length(downT{i}),downT{i});
line(1:length(downT{i}),upT{i},’color’,’r’,’Marker’,’.’);
end
% INDEXES calculation
average_interuption = interuption/duration;
average_outage_time = outage_time/duration;
customers_num = sum(users);
total_power = sum(power);
SAIFI = average_interuption*customers_num/customers_num;
SAIDI = average_outage_time*customers_num/customers_num;
CAIDI = SAIDI/SAIFI;
ASAI = (customers_num*8760 - average_outage_time*customers_num)/ (customers_num*8760);
EUE = average_outage_time*total_power; % kW*hour
disp(‘-------------------------------’);
disp(‘Step 1’);
disp([‘SAIFI ‘ num2str(SAIFI)]);
disp([‘SAIDI ‘ num2str(SAIDI)]);
disp([‘CAIDI ‘ num2str(CAIDI)]);
disp([‘ASAI ‘ num2str(ASAI)]);
disp([‘EUE ‘ num2str(EUE)]);
%% Step2 switches
switch_834_lines = [20 21 22 31 32];
switch_832_lines = [17 18 19 30 23 24 25 switch_834_lines];
switch_834_elements = [19 20 21 30 31];
switch_832_elements = [switch_834_elements 18 22 23 24 25 29 32];
interaptionXcustomer_number = 0;
interaptionXcustomer_duration = 0;
unservedEnergy = 0;
cur_t = 0;
while cur_t < maxT
% find next failure time
min_t = (duration + 1)*24*365;
fail_line_number = 0;
for i = 1:N
clear indx;
indx = find(downT{i} > cur_t);
if (~isempty(indx))
indx = indx(1);
if (downT{i}(indx) < min_t)
min_t = downT{i}(indx);
fail_line_number = i;
n = indx;
cur_outage_time = upT{i}(indx) − downT{i}(indx);
end
end
end
cur_t = upT{fail_line_number}(n);
in_switch_834 = ~isempty(find(switch_834_lines == fail_line_number));
customer_834 = sum(users(switch_834_elements));
power_834 = sum(power(switch_834_elements));
in_switch_832 = ~isempty(find(switch_832_elements == fail_line_number));
customer_832 = sum(users(switch_832_elements));
power_832 = sum(power(switch_832_elements));
% interaption calculation
if (~in_switch_832)
interaptionXcustomer_number = interaptionXcustomer_number + customers_num;
interaptionXcustomer_duration = interaptionXcustomer_duration + customers_num*cur_outage_time;
unservedEnergy = unservedEnergy + total_power*cur_outage_time;
else
if (in_switch_834)
interaptionXcustomer_number = interaptionXcustomer_number + customer_834;
interaptionXcustomer_duration = interaptionXcustomer_duration + customer_834*cur_outage_time;
unservedEnergy = unservedEnergy + power_834*cur_outage_time;
else
interaptionXcustomer_number = interaptionXcustomer_number + customer_832;
interaptionXcustomer_duration = interaptionXcustomer_duration + customer_832*cur_outage_time;
unservedEnergy = unservedEnergy + power_832*cur_outage_time;
end
end
end
% INDEXES calculation
SAIFI = interaptionXcustomer_number/customers_num/duration;
SAIDI = interaptionXcustomer_duration/customers_num/duration;
CAIDI = SAIDI/SAIFI;
ASAI = (customers_num*8760 − interaptionXcustomer_duration/duration)/ (customers_num*8760);
EUE = unservedEnergy/duration; % kW*hour
disp(‘-------------------------------’);
disp(‘Step 2’);
disp([‘SAIFI ‘ num2str(SAIFI)]);
disp([‘SAIDI ‘ num2str(SAIDI)]);
disp([‘CAIDI ‘ num2str(CAIDI)]);
disp([‘ASAI ‘ num2str(ASAI)]);
disp([‘EUE ‘ num2str(EUE)]);
%% Step 3 switches from Step 2 and DGs
switch_834_lines = [20 21 22 31 32];
switch_832_lines = [17 18 19 30 23 24 25 switch_834_lines];
switch_834_elements = [19 20 21 30 31];
switch_832_elements = [switch_834_elements 18 22 23 24 25 29 32];
interaptionXcustomer_number = 0;
interaptionXcustomer_duration = 0;
unservedEnergy = 0;
cur_t = 0;
while cur_t < maxT
% find next failure time
min_t = (duration + 1)*24*365;
fail_line_number = 0;
for i = 1:N
clearindx;
indx = find(downT{i} > cur_t);
if (~isempty(indx))
indx = indx(1);
if (downT{i}(indx) < min_t)
min_t = downT{i}(indx);
fail_line_number = i;
n = indx;
cur_outage_time = upT{i}(indx) − downT{i}(indx);
end
end
end
cur_t = upT{fail_line_number}(n);
in_switch_834 = ~isempty(find(switch_834_lines == fail_line_number));
customer_834 = sum(users(switch_834_elements));
power_834 = sum(power(switch_834_elements));
in_switch_832 = ~isempty(find(switch_832_elements == fail_line_number));
customer_832 = sum(users(switch_832_elements));
power_832 = sum(power(switch_832_elements));
customer_800 = customers_num-customer_832;
power_800 = total_power-power_832;
% interaption calculation
if (~in_switch_832)
interaptionXcustomer_number = interaptionXcustomer_number + customer_800;
interaptionXcustomer_duration = interaptionXcustomer_duration + customer_800*cur_outage_time;
unservedEnergy = unservedEnergy + power_832*cur_outage_time;
else
if (in_switch_834)
interaptionXcustomer_number = interaptionXcustomer_number + customer_834;
interaptionXcustomer_duration = interaptionXcustomer_duration + customer_834*cur_outage_time;
unservedEnergy = unservedEnergy + power_834*cur_outage_time;
else
interaptionXcustomer_number = interaptionXcustomer_number + customer_832;
interaptionXcustomer_duration = interaptionXcustomer_duration + customer_832*cur_outage_time;
unservedEnergy = unservedEnergy + power_832*cur_outage_time;
end
end
end
% INDEXES calculation
SAIFI = interaptionXcustomer_number/customers_num/duration;
SAIDI = interaptionXcustomer_duration/customers_num/duration;
CAIDI = SAIDI/SAIFI;
ASAI = (customers_num*8760 − interaptionXcustomer_duration/duration)/ (customers_num*8760);
EUE = unservedEnergy/duration; % kW*hour
disp(‘-------------------------------’);
disp(‘Step 3’);
disp([‘SAIFI ‘ num2str(SAIFI)]);
disp([‘SAIDI ‘ num2str(SAIDI)]);
disp([‘CAIDI ‘ num2str(CAIDI)]);
disp([‘ASAI ‘ num2str(ASAI)]);
disp([‘EUE ‘ num2str(EUE)]);
Abbreviations and Acronyms
IEEE: Institute of Electrical and Electronics Engineering.
AR: Automatic Recloser.
SAIDI: System Average Interruption Duration Index.
DG: Distributed Generation.
CAIDI: Customer Average Interruption Duration Index.
U: Annual Unavailability Time.
EUE: Expected Un-served Energy.
R: Annual Outage Time.
λ: Failure Rate of an Electrical Component.
TTR: Mean Time to Repair.
TTF: Mean Time to Fail.
MCS: Monte Carlo Simulation.