On Decomposition of New Kinds of Continuity in Bitopological Space

H. Al-Malki¹, S. Al-Blowi²

¹Department of Mathematics, University College in Adam, Umm Al Qura University, Makkah, Saudi Arabia.
²Department of Mathematics, Faculty of Science for Girls, King Abdulaziz University, Jeddah, Saudi Arabia.

DOI: 10.4236/ijmnta.2017.63009                

Abstract

In many papers, new classes of sets had been studied in topological space, then the notion of continuity between any two topological spaces (a function from X to Y is continuous if the inverse image of each open set of Y is open in X) is studied via this new classes of sets. Here the authors also introduce new classes of sets called pj-b-preopen, pj-b-B set, pj-b-t set, pj-b-semi-open and pj-sb-generalized closed set in bitopological space [1] which is a set with two topologies defined on it, then they study the notion of continuity via this set and introduce some of the theories which are studying the decomposition of continuity via this set in bitopological space.

Keywords

pj-b-Preopen, pj-b-Semiopen, pj-b-t Set, pj-b-B Set, pj-sb-Generalized Closed, Bitopological Space

1. Introduction and Preliminaries

In topological space, there are many classes of generalized open sets given by [2] [3] [4] [5] . Tong [6] introduced the concept of t-set and B-set in topological space. [7] [8] gave some decomposition of continuity. Decomposition of pair- wise continuity was given by Jelice [9] and [10] [11] [12] . In this paper, we introduce decomposition of continuity in bitopological space via new classes of sets called pj-b-preopen, pj-b-B set, pj-b-t set, pj-b-semi-open and pj-sb-genera- lized closed set with some theories, examples and results.

Definition 1.1. Let 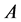be a subset of a space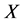, then 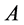is said to be:

1) b-t-set [7] if.

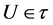2) b-B-set [7] if, where and 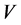is a b-t-set.

3) Locally b-closed [7] if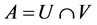, where 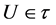and 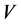is a b-closed set.

4) b-preopen [7] if.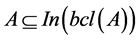

5) b-semiopen [7] if.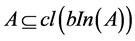

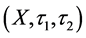Definition 1.2. Let be a subset of a bitopological space then 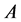called pairwise p-open (or p-open) [11] if. p-closed is the com- plement of p-open set. p-interior of 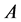(or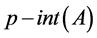) is the union of all p-open sets of a bitopological space which contained in a subset of. Also, the p-closure of (or) is the intersection of all p-closed sets which containing.

Definition 1.3. A subset of a bitopological space is said to be:

1) pj-b-open [10] if.

2) pj-b-closed [10] if.

3) pj-semiopen [11] if.

4) pj-preopen [11] if.

5) pj-t-set [12] if.

6) pj-B-set [12] if, where is p-open and is a pj-t-set.

7) jp-regular open [12] if.

2. pj-b-t-Set, pj-b-B-Set pj-b-Semiopen, pj-b-Preopen and pj-sb-Generalized Closed

In this section, we investigated our new classes of sets pj-b-preopen, pj-b- semiopen, pj-b-t set, pj-b-B set and pj-sb-generalized closed set and study some of its fundamental properties and examples also we introduce some of important theories which is useful to study the decomposition of continuity via our new classes of sets.

Definition 2.1. A subset of a bitopological space is said to be:

1) pj-b-t-set if.

2) pj-b-B-set if, where is p-open and is a pj-b-t-set.

3) pj-b-semiopen if.

4) pj-b-preopen if.

Example 2.2. Let, and then is a p2-b-t-set.

Example 2.3. Let and and then is a p1-b-B-set.

Example 2.4. Let and and then it is p1-b-preopen.

Proposition 2.5. If and are a subsets of a bitopological space, then

1) is a pj-b-t set if and only if is pj-b-semiclosed.

2) If is pj-b-closed, then it is a pj-b-t-set.

3) If and are pj-b-t-sets, then is a pj-b-t-set.

proof. 1) Let be pj-b-t set, then that implies is pj-b-semiclosed. conversely, Let be pj-b-semiclosed set, then . Also, and. Hence, is a pj-b-t set.

2) Let be pj-b-closed, then .

3) Let and be pj-b-t-sets, then we have:

, Hence is a pj-b-t-set.

The following example shows that the converse of (2) is not true in general.

Example 2.6. From example 2.2 it is clear that is a p2-b-t-set but it is not p2-b-closed.

Lemma 2.7. Let be p-open subset of a bitopological space, then

and .

proof. Let be p-open subset of, then

Proposition 2.8. Let be a subsets of a bitopological space, then

1) If is pj-t-set then it is pj-b-t-set.

2) If is pj-b-t-set then it is pj-b-B-set.

3) If is pj-B-set then it is pj-b-B-set.

proof. 1) Let be pj-t-set,then from lem- ma 2.1 . Hence is pj-b-t-set.

2) Let be pj-b-t-set. and is p-open set, then is pj-b- B-set.

3) Let be pj-B-set i.e., where is p-open and is a pj-t- set i.e. from lemma 2.1 . Hence is pj-b-B-set.

Theorem 2.9. Let be a subset of a bitopological space, then the following are equivalent:

1) is p-open set.

2) is pj-b-preopen and pj-b-B-set.

proof. (1) Þ (2) Let be p-open but then is pj-b-preopen. Also, and is p-open and is pj- b-B-set.

(2) Þ (1) be pj-b-preopen and pj-b-B-set. i.e., where is p-open and, then we have

Hence,

Therefore and is p-open.

The following examples show that pj-b-preopen sets and pj-b-B-sets are independent.

Example 2.10. From example 2.3 it is clear that is a p1-b-B -set but it is not p1-b-preopen.

Example 2.11. From example 2.4 it is clear that it is p1-b-preopen but it is not a p1-b-B-set.

Corollary 2.12. A subset of a bitopological space is p-open if and only if it is pj-α-open and pj-b-B-set.

Proposition 2.13. Let be a subsets of a bitopological space, then the following are equivalent:

1) is jp-regular set.

2)

3) is pj-b-preopen and pj-b-t-set.

proof. (1) Þ (2) Let be jp-regular set.since then . Since is pj-b-open . Hence,

(2) Þ (3) This is obvious.

(3) Þ (1) Let be pj-b-preopen and pj-b-t-set.Then and is p-open by lemma 2.1 Hence, is jp-regular set.

Definition 2.14. A subset of a bitopological space is called pj-sb- generalized closed if pj-, whenever and is pj-b- preopen.

Definition 2.15. pj- is the intersection of all pj-semiclosed sets which containing.

Theorem 2.16. Let be a subset of a bitopological space, the following properties are equivalent:

1) is jp-regular open set.

2) is pj-b-preopen and pj-sb-generalized closed set.

proof. (1) Þ (2) Let be jp-regular open.Then is pj-b-open. . Moreover, by Lemma 2.1 pj-. Hence, is pj-sb-generalized closed.

(2) Þ (1) Let be pj-b-preopen and pj-sb-generalized closed. is pj-b-semiclosed. Then . Therefore by Proposition 2.3 A is jp-regular open.

Corollary 2.17. A subset of a bitopological space is jp-regular open if and only if it is pj-α-open and pj-b-t-set.

3. Decompositions of New Kinds of Continuity

After we had been defined and studied the propriety of our new classes of sets we are ready to study the concept of continuity between any two bitopological spaces via our new classes of sets.

Definition 3.1. A function is called pj-b-conti- nuous [10] (resp. pj-Locally b-closed continuous [10] , pj-D(c,b)-continuous [10] , pj-α-continuous [11] pj-semi continuous [11] , jp-semi continuous [11] , pj-B- continuous [12] , pj-Locally closed continuous [12] , jp-regular continuous [13] ) if is pj-b-set (resp. pj-Locally b-closed set, pj-D(c,b)-set, pj-α-open, pj-semiopen, jp-semiopen, pj-B-set, pj-Locally closed,, jp-rgular) in for each p-open set V of Y.

Theorem 3.2. A function is called pj-B-conti- nuous if and only if it is locally pj-b-closed-continuous and pj-semi-continuous.

proof. It is following from lemma 3.4 in [10]

Definition 3.3. Afunction is called pj-b-pre-con- tinuous (resp. pj-b-B-continuous, pj-b-t-continuous, pj-b-semi-continuous) if is pj-b-preopen (resp. pj-b-B-set, pj-b-t-set, pj-b-semiopen) in for each p-open set of.

Theorem 3.4. A function is called p-continuous if and only if it is pj-α-continuous and pj-b-B-continuous.

proof. It is follows from theorem 2.1.

Theorem 3.5. A function is called p-continuous if and only if it is pj-b-pre-continuous and pj-b-B-continuous.

proof. It is follows from corollary 2.1.

Definition 3.6. Afunction is called contra pj-sb- continuous if is pj-sb-generalized closed in for each p-open set of.

Theorem 3.7. A function is called completely p- continuous if and only if it is pj-b-pre-continuous and pj-b-t-continuous.

proof. It is follows from proposition 2.3.

Theorem 3.8 A function is called completely p-continuous if and only if it is pj-b-pre-continuous and contra pj-sb-con- tinuous.

proof. It is follows from theorem 2.2.

Theorem 3.9 A function is called completely p- continuous if and only if it is pj-α-continuous and pj-b-t-continuous.

proof. It is follows from corollary 2.2.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kelly, J.C. (1963) Bitopological Space. Proceedings of the London Mathematical Society, 13, 71-89. https://doi.org/10.1112/plms/s3-13.1.71
[2]	Andrijevic, D. (1996) On B-Open Sets. Matematichki Vesnik, 48, 59-64.
[3]	Andrijevic, D. (1986) Semi-Preopen Sets. Matematichki Vesnik, 38, 24-32.
[4]	Levine, N. (1861) A Decomposition of Continuity in Topological Spaces. American Mathematical Monthly, 68, 44-46. https://doi.org/10.2307/2311363
[5]	Njastad, O. (1965) On Some Classes of Nearly Open Sets. Pacific Journal of Mathematics, 15, 961-970. https://doi.org/10.2140/pjm.1965.15.961
[6]	Tong, J. (1989) On Decomposition of Continuity in Topological Spaces. Acta Mathematica Hungarica, 54, 51-55. https://doi.org/10.1007/BF01950708
[7]	Al-Omari, A. and Noorani, M. (2008) Decomposition of Continuity via B-Open Set. Boletim da Sociedade Paranaense de Matematica, 26, 53-64. https://doi.org/10.5269/bspm.v26i1-2.7402
[8]	Przemski, M.A. (1993) Decomposition of Continuity and α-Continuity. Acta Mathematica Hungarica, 61, 93-98. https://doi.org/10.1007/BF01872101
[9]	Jelic, M. (1990) A Decomposition of Pairwise Continuity. J. Inst. Math. Comput. Sci. Math. Ser., 3, 25-29.
[10]	Al-Blowi, S.A. (2017) Decomposition of P-Continuity via PG-B-Open Set, PG-Locally B-Closed and PJ-D (c, b)-Set.
[11]	Khedr, F.H. and Al-Blowi, S.A. (2007) PJ-Γ Sets and PJ-Γ-Continuity in Bitobological Space (I). Journal of Mathematics and Computer Science, 36, 1-19.
[12]	Khedr, F.H. and Al-Blowi, S.A. (2007) PJ-Γ Sets and PJ-Γ-Continuity in Bitobological Space (II). Journal of Mathematics and Computer Science, 36, 21-41.
[13]	Arya, S.R. and Gupta, R. (1974) On Strongly Continuous Mappings. Kyungpook Mathematical Journal, 14, 131-143.