Investigation of a New Waveguide Structure Based on Negative Index Material for Optoelectronic Applications ()
1. Introduction
Negative index materials (NIM) are artificially designed structures with negative permittivity and permeability providing a route to create potential devices with fascinating electromagnetic properties that cannot be obtained with natural materials [1] - [6] . The history of these materials began with Veselago [7] who predicted the existence of such materials with unexpected optical properties. One particularly interesting NIM device is an NIM based waveguide structure that has potentially interesting applications. Recent experimental demonstrations of novel composite materials with a negative refractive index [8] - [13] open up an exceptional possibility to design novel types of devices where electromagnetic waves propagate in a nonconventional way. In parallel, more linear and nonlinear metamaterials have been studied theoretically and experimentally from microwave to optical frequencies [14] - [19] . In most investigations dealing with the planar nonlinear waveguides, the basic attention has been given to the electromagnetic surface waves [20] . Despite these advanced studies, new modes of propagation due to the variation of NIM’s parameters (permittivity and permeability) in new NIM waveguide were not investigated. In this paper, we aim at studying a magnetic structure with a negative index material (NIM) core surrounded by a nonlinear cover cladding and a ferrite substrate, where unusual electromagnetic surface waves-basically not existing in a conventional waveguide-are examined [21] . The present work is an extension and an integration of the previous work [12] [21] . We focus on studying the considered structure and calculate the dispersion equations for TE modes. We present and discuss the associated propagation wave index and the film cover interface nonlinearity versus the normalized frequency and other various physical parameters of the NIM layer. The numerical results are given in order to draw attention on the variation in surface wave’s behavior propagating in different waveguide structures, as in the considered waveguide based on NIM core [13] [22] having negative permittivity
and permeability
both depending on the operating frequency
, the NEM waves propagate in a non-conventional way comparing with those propagating in classical structures. Finally, conclusions are given for the various results of this study. This work’s results can be used in designing and fabricating microwave devices for a wide range of applications as isolators, sensors, circulators, solar cells…
2. Proposed Waveguide Structure and Simulation Approach
Figure 1 displays the configuration of the considered waveguide structure. We shall assume that the waveguide consists of an NIM core of width L bounded by a nonlinear cover and a gyromagnetic ferrite substrate. The waveguide is assumed to have infinite extent in the x and y directions. The dispersion equation is given for stationary TE waves only propagating in the x-direction. A static magnetic field is applied in the y direction transverse to the direction of propagation.
The magnetic permeability tensor of the ferrite (YIG) substrate is defined as [21] where 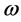 is the surface wave operating frequency:
is the surface wave operating frequency:
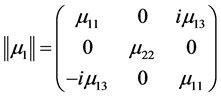 where
where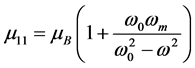 and
and 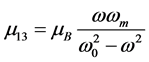 and
and .
.
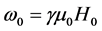 is the Larmor frequency,
is the Larmor frequency, 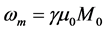 is the magnetic frequency,
is the magnetic frequency,  is the background permeability,
is the background permeability, 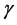 is the gyromagnetic ratio,
is the gyromagnetic ratio, 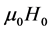 is
is
![]()
Figure 1. The schematic of the proposed waveguide consisting of negative index film bounded by a ferrite (YIG) substrate and a nonlinear (NL) cover.
the applied magnetic field and  is the dc saturation magnetization. The
is the dc saturation magnetization. The
NIM core has it effective permittivity 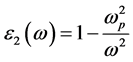 with the plasma fre-
with the plasma fre-
quency 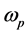 in the GHz range and it effective magnetic permeability
in the GHz range and it effective magnetic permeability
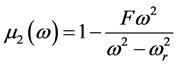 , with the resonance frequency
, with the resonance frequency  in the GHz range; F is
in the GHz range; F is
the filling factor. We choose 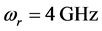 and
and
F = 0.56 [22] . The nonlinear dielectric cover has it dielectric function isotropic and depends on the electric field. It can be written as for TE waves: 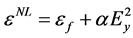 where
where ![]() is the linear part of the dielectric function and
is the linear part of the dielectric function and ![]() is the nonlinear coefficient [21] .
is the nonlinear coefficient [21] .
The TE fields have the following forms, where q is the propagation constant:
![]()
![]() (1)
(1)
We apply the transverse electric fields into Maxwell's equations:
![]() (2)
(2)
![]() (3)
(3)
In the ferrite (YIG) substrate, the plane wave equation is:
![]() (4)
(4)
where ![]() and
and ![]() is the Voigt permeability,
is the Voigt permeability, ![]() is the effective mode index,
is the effective mode index, ![]() is the propa-
is the propa-
gation constant in the vacuum, and c is the speed of light.
In medium (2), the plane wave equation is:
![]() (5)
(5)
where:
![]()
In the nonlinear dielectric cover, the plane wave equation is:
![]() (6)
(6)
where:
![]()
Applying the boundary conditions at z = 0 and z = L to the plane wave equations solutions, we obtain the dispersion equation as follows:
![]() (7)
(7)
where:
![]() and
and ![]()
is a constant that we can determine from the boundary conditions.
From the nonlinear dispersion equation we can easily obtain the film-cover interface nonlinearity:
![]() (8)
(8)
![]() ,
,
![]()
3. Results and Discussions
In order to have surface waves in the proposed waveguide structure, the effective ferrite permeability should be less than zero. This constraint and condition should be implemented on the solution of the dispersion equation. We numerically solve the Equation (7) in order to find out the propagation wave index versus the operating normalized frequency ![]() for different NIM film thicknesses L, where
for different NIM film thicknesses L, where![]() . The numerical computations were performed the parameter values [15] :
. The numerical computations were performed the parameter values [15] :![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Figure 2 shows the computed effective Voigt permeability ![]() versus the normalized operating frequency. For numerical calculation, we set the frequency within the range from
versus the normalized operating frequency. For numerical calculation, we set the frequency within the range from ![]() to
to ![]() for
for![]() .
.
Figure 3 shows discontinuity, that represents the forbidden band of the NIM waveguide. It clearly illustrates that the surface modes cannot propagate for L = 4 mm.
Figure 4 shows the NEM surface waves dispersion in the backward wave direction. Different NIM slab thicknesses are considered to show it effect on the propagation. The effective wave index versus the operating frequency has a new
![]()
Figure 2. The effective Voigt permeability versus the normalized frequency.
![]()
Figure 3. The dependence of Ω on the wave index for the negative NIM layer thickness L = 4 mm.
![]()
Figure 4. NEM surface wave’s dispersion in the backward wave direction for different values of the NIM slabs thickness.
different behavior, we can observe that when the value of L increases from 0.15 mm to 0.55 mm, the wave index varies from 0.2 to 0.55, above the value![]() , the propagation modes become identical and have practically the same trajectory.
, the propagation modes become identical and have practically the same trajectory.
Figure 5 exhibits the nonlinear surface wave’s dispersion curves in the backward and the forward directions for different NIM slab thicknesses with the film cover non-linearity value kept constant. The curves present a linear increase with practically the same direction. Moreover all modes are propagating in the negative region for ![]() negative in the forward direction and propagating in the positive region for
negative in the forward direction and propagating in the positive region for ![]() positive in the backward direction. We conclude that the NIM having it permittivity and permeability depending on the frequency is changing the forward direction to the backward direction and this behavior is particular to NIM based waveguides.
positive in the backward direction. We conclude that the NIM having it permittivity and permeability depending on the frequency is changing the forward direction to the backward direction and this behavior is particular to NIM based waveguides.
It is concluded that by adjusting or tuning some physical parameters in such waveguide structure, the wave propagation direction could be reversed. This feature or characteristics could be used in design some future optoelectronics devices.
Figure 6 shows NEM surface wave’s dispersion curves in the backward and the forward directions for different NIM slab thicknesses and for a different value of nonlinearity ![]() with the film cover non-linearity value kept constant. We found that two different values of the frequency correspond to the same value of the wave index; this also means that both figures show a new behavior and different stability features. This behavior is very important to design microwave devices.
with the film cover non-linearity value kept constant. We found that two different values of the frequency correspond to the same value of the wave index; this also means that both figures show a new behavior and different stability features. This behavior is very important to design microwave devices.
The above predictions and calculations of NEM surface wave contrast behavior might be used in designing future microwave devices such as isolators and circulators.
4. Conclusion
In a three-layered structure based on NIM having it optical parameters (permittivity and permeability) depending on the operating frequency, the propagation characteristics can be controlled by selecting the NIM film thickness. The negative effect of the NIM core is reversing the forward direction of the waves to be in the backward direction. Moreover, for some values of the wave index in the backward propagation direction (or forward propagation direction) correspond two operating frequencies. These effects are in contrast with those obtained in a conventional waveguide structure and could be used in designing and implementing integrated microwave devices based on the non-reciprocal behavior as isolators, sensors and circulators for military services, solar cells, telecommunications, automatic access control systems and medical equipment.
Acknowledgements
One of the authors (M.M.S) thanks Prof. Dr. Daniel M. Schaadt, Institute of Energy Research and Physical Technologies, Technical University of Clausthal, Germany for many valuable suggestions and fruitful discussions during the development of this work.