Finite Element Analysis and Test of an Ultrasonic Compound Horn ()
1. Introduction
Ultrasonic horn is very important in high power ultrasound equipment in the vibration system, the main function is to amplify the displacement and velocity of mechanical vibration particle, or concentrate the ultrasonic energy on a small area [1] . Because of the important role of ultrasonic machining system, scholars have carried out a great deal of research on the horn [2] [3] [4] [5] . According to the vibration type, ultrasonic horn can be divided into four types: longitudinal vibration, torsional vibration, flexural vibration and compound vibration. And ultrasonic horn can be divided into ladder, index and cone according to the shape of generatrix. In order to obtain large amplitude ultrasonic horn, a compound horn with ladder and cone is designed in this paper. The finite element analysis and test of the horn are carried out. The theoretical and experimental results show that the horn has the characteristics of high sensitivity and large amplitude. It can be used in ultrasonic machining and other fields.
2. The Structure and Working Principle of Ultrasonic Horn
The structure of the ultrasonic horn was shown in Figure 1. The horn was composed of a counterweight block 1, a counterweight block 2, a piezoelectric ceramic, a connecting disk, a cone and a tool rod. The counterweight block 1 and 2 were used for fixing the piezoelectric ceramic and could adjust the natural frequency of the ultrasonic vibrator.
The piezoelectric ceramic plate is made of a plurality of ceramic pieces. Layout of ceramic plate adopts homopolarly opposite placed, and ensure elongation and contraction of ceramic plates. When the applied electric field direction is in accordance with the polarization direction of the ceramic plate, according to the piezoelectric vibration mode, the ceramic plate produces an elongation deformation, and conversely the ceramic sheet shrinks.
The shape of the cone and stepped cylinder can amplify the amplitude.
3. Working Principle of the Ultrasonic Horn [1]
The ultrasonic horn is to enlarge the particle displacement or velocity of mechanical vibration, and its performance parameters include resonance frequency, amplification coefficient and so on. The amplification factor is the ratio of the particle displacement or velocity amplitude between the output and the input at the resonant frequency of the ultrasonic horn. The working principle of the ultrasonic is explained by a stepped shape which is shown in Figure 2.
The symmetrical axis of the horn is shown in Figure 2. It is assumed that the stresses on the cross section of the rod are uniformly distributed and that the stepped deflection bar is composed of two uniform bars with different sectional areas. The wave equation is as follows.
 (1)
(1)
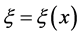 is the particle displacement function in the formula,
is the particle displacement function in the formula,  ,
,  is the circular wave number,
is the circular wave number,  is the circle frequency,
is the circle frequency, 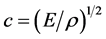 is the propagation velocity of longitudinal waves in an amplitude horn. By Equation (1) the solvable particle displacement is:
is the propagation velocity of longitudinal waves in an amplitude horn. By Equation (1) the solvable particle displacement is:
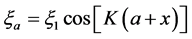 (2)
(2)
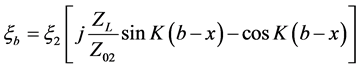 (3)
(3)
In the formula,  is the load force impedance.
is the load force impedance.
When the horn has no load, that is, 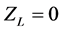 , by
, by 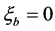 the displacement
the displacement
node can be obtained 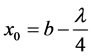 (a is the wavelength of longitudinal wave propagation in an amplitude horn). When
(a is the wavelength of longitudinal wave propagation in an amplitude horn). When ,
, 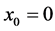 that indicates that it is located in the center of the horn.
that indicates that it is located in the center of the horn.
The amplitude ratio of the top and the end of the horn is the magnification factor which can be represented as:
 (4)
(4)
By the formula (3), displacement node has something to do with influence factors including the length of big end and small end of the stepped ultrasonic horn, the material and so on.
By the formula (4), the amplitude ratio at the top and end of the horn has something to do with influence factors including the diameter of big end and small end of the stepped ultrasonic horn, circular wave number and so on.
4 Finite Element Analysis of the Ultrasonic Horn
The finite element model of the ultrasonic horn shown in Figure 3 is established in Ansys software. The material of piezoelectric ceramics is selected as PZT-8 and its parameters are shown in Table 1. The material of the other parts is selected as 45 steel. The solid 5 element is used to mesh the piezoelectric ceramics, and the solid 45 element are used to mesh the remaining metals in Ansys software.
Modal analysis is carried out for the finite element model of the ultrasonic horn shown in Figure 4(a). The frequency of the first longitudinal vibration of the ultrasonic horn is 14,501 Hz, and the mode of vibration is shown in Figure 6.
The frequency of the second longitudinal vibration of the ultrasonic horn is 20,350 Hz, and the mode of vibration is shown in Figure 4(b).
![]()
Figure 3. The finite element model of the ultrasonic horn.
![]()
Table 1. Material parameters of PZT-8.
![]() (a)
(a)![]() (b)
(b)
Figure 4. (a) The first order longitudinal vibration mode; (b) The second order longitudinal vibration mode.
5. Modal Testing of Ultrasonic Horn
According to the theoretical analysis, the ultrasonic horn was made. The object was shown in Figure 5.
Modal testing of the ultrasonic horn was performed by using PSV-500 Doppler scanning laser vibrometer. The section of small end of the ultrasonic horn was swept by the laser vibrometer, and the sweep frequency range was 0 - 25 khz. The excitation voltage increases from zero, and when 7 V is reached, the response diagram of the ultrasonic horn within the 0 - 25 khz frequency range can be measured and shown in Figure 6.
As could be seen from Figure 6, the horn had two peak points in the 0 - 25 khz frequency range, The frequencies of the two peaks were 17,248 Hz and 21,646 Hz respectively.
When the excitation voltage amplitude was 7 V, the vibration of the end surface could be measured axially at two frequencies of 17,248 Hz and 21,646 Hz respectively. When the excitation frequency was 21,646 Hz, the displacement response of the ultrasonic horn was shown in Figure 7.
In order to determine the axial mode shapes of the ultrasonic horn, the horn was tilted and the exciting signal was applied under the same conditions. When the excitation signal voltage was 7 V and the frequency was 17,248 Hz, the frequency sweep was carried out along the axial direction of the ultrasonic horn, and the modal shape of the ultrasonic horn could be measured as shown in Figure 8. As could be seen from Figure 8, the maximum amplitude was located at the small end of the ultrasonic horn, approximately 3 nm.
When the excitation signal voltage was 7 V and the frequency was 21,646 khz, the frequency sweep was carried out along the axial direction of the ultrasonic
![]()
Figure 6. The frequency response diagram of the ultrasonic horn.
![]()
Figure 7. The displacement response of the ultrasonic horn.
![]()
Figure 8. The modal shape along the axial direction (17,248 Hz).
![]()
Figure 9. The modal shape along the axial direction (21,646 Hz).
![]()
Figure 10. The maximum amplitude of the ultrasonic horn varied with the amplitude of the voltage.
horn, and the modal shape of the ultrasonic horn could be measured as shown in Figure 9. As could be seen from Figure 9, the maximum amplitude was located at the small end of the ultrasonic horn, approximately 9 nm.
When the frequency of the excitation signal was set as 21,646 khz, and the voltages were set to 20 V, 40 V, 60 V and 80 V respectively, the maximum amplitude of the horn varied with the amplitude of the voltage, as shown in Figure 10.
When the excitation frequency is 21,646 khz, the amplitude is 80 V, the maximum amplitude of the ultrasonic horn could reach 23 µm. The ultrasonic horn could be used in ultrasonic machining and other fields
6. Conclusion
An ultrasonic horn is designed, and the finite element analysis and modal experiment are carried out. The maximum amplitude of the horn can reach 9 nm with applied excitation voltage of amplitude 7 V and frequency 21,450 Hz, when the amplitude of voltage increases to 80 V, the horn of maximum amplitude reaches 23 µm. The maximum amplitude of the horn is approximately proportional to the amplitude of excitation voltage. The horn has the characteristics of high sensitivity and large amplitude, and can be used in ultrasonic machining and other fields.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No.50865181) and Qinlan Project.