Solvability of Chandrasekhar’s Quadratic Integral Equations in Banach Algebra

Hind H. G. Hashem¹, Aml A. Alhejelan²

¹Faculty of Science, Alexandria University, Alexandria, Egypt.
²Collage of Science, Qassim University, Buraidah, KSA.

DOI: 10.4236/am.2017.86066                

Abstract

In this paper, we prove some results concerning the existence of solutions for some nonlinear functional-integral equations which contain various integral and functional equations that are considered in nonlinear analysis. Our considerations will be discussed in Banach algebra using a fixed point theorem instead of using the technique of measure of noncompactness. An important special case of that functional equation is Chandrasekhar’s integral equation which appears in radiative transfer, neutron transport and the kinetic theory of gases [1].

Keywords

Nonlinear Operators, Banach Algebra, Chandrasekhar’s Integral Equations

1. Introduction

Functional integral and differential equations of different types play an im- portant and a fascinating role in nonlinear analysis and finding various ap- plications in describing of several real world problems [2] [3] [4] [5] [6] [7] [8] [9] .

Nonlinear functional integral equations have been discussed in the literature extensively, for a long time. See for example, Subramanyam and Sundersanam [10] , Ntouyas and Tsamatos [11] , Dhage and O’Regan [12] and the references therein.

Dhage [12] and [13] initiated the study of nonlinear integral equations in a Banach algebra via fixed point techniques instead of using the technique of measure of noncompactness.

Dhage [14] studied the existence of the nonlinear functional integral equation (in short FIE)

$x\left(t\right)=k\left(t,x\left(\mu \left(t\right)\right)\right)+\left[f\left(t,x\left(\nu \left(t\right)\right)\right)\right]\cdot \left(q\left(t\right)+{\displaystyle {\int }_0^{\sigma \left(t\right)}}g\left(s,x\left(\eta \left(s\right)\right)\right)\text{d}s\right)$

by using fixed point theorems concerning the nonlinear alternative of Leray- Schauder type which are proved in [14] .

Banaś and Sadarangani [15] discussed the existence of solutions for a general NLFIE

$x\left(t\right)=f\left(t,{\displaystyle {\int }_0^t}v\left(t,s,x\left(s\right)\right)\text{d}s,x\left(\alpha \left(t\right)\right)\right)\cdot g\left(t,{\displaystyle {\int }_0^a}u\left(t,s,x\left(s\right)\right)\text{d}s,x\left(\beta \left(t\right)\right)\right)$

using the technique of measure of noncompactness in Banach algebra. Also, an existence results for Chandrasekhar’s integral equation was deduced.

A fixed point theorem involving three operators in a Banach algebra by blending the Banach fixed point theorem with that Schauder’s fixed point principle was proved by B. C. Dhage in [16] . The existence of solutions of the equation

$x=AxBx+Cx$

are proved in (see [14] [17] - [22] , and the references therein). These studies were mainly based on the convexity and the closure of the bounded domain, the Schauder fixed point theorem [13] [14] .

In this paper, instead of using the technique of measure of noncompactness in Banach algebra, we shall use Dhage fixed point theorem [20] to prove an existence theorem for a nonlinear functional integral equation

$x\left(t\right)=f\left(t,x\left(t\right)\right)+g\left(t,x\left(t\right)\right)\cdot \psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x\left(s\right)\right)\text{d}s\right),\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J=\left[0,b\right].$ (1)

An important special case of the functional Equation (1) is Chandrasekhar’s integral equation

$x\left(t\right)=1+x\left(t\right){\displaystyle {\int }_0^1}\frac{t}{t+s}\phi \left(s\right)x\left(s\right)\text{d}s$

which appears in in radiative transfer, neutron transport and the kinetic theory of gases [1] [2] [23] .

Our paper is organized as: In Section 2, we introduce some preliminaries and use them to obtain our main results in Section 3. In Section 4, we provide some examples and special cases that verify our results. In the last section, further existence results has been proved.

2. Preliminaries

In this section, we collect some definitions and theorems which will be needed in our further considerations.

Let $J=\left[0,b\right]$ and $X=ℂ\left(J,ℝ\right)$ denotes the space of all continuous real- valued functions on J equipped with the norm $\Vert x\Vert =\underset{t\in J}{{\displaystyle \sup }}$ . Clearly, $ℂ\left(J,ℝ\right)$ is a complete normed algebra with respect to this supremum norm.

A normed algebra is an algebra endowed with a norm satisfying the following property, for all $x\mathrm{,}y\in X$ we have

$\Vert x\cdot y\Vert \le \Vert x\Vert \cdot \Vert y\Vert .$

A complete normed algebra is called a Banach algebra.

Let $L^1=L^1[J]$ be the class of Lebesgue integrable functions on J with the standard norm.

Definition 1. [20] A mapping $T\mathrm{<mo>\; :\; </mo>}X\to X$ is called totally bounded if $T\left(S\right)$ is a totally bounded subset of X for any bounded subset S of X. Again a map $T\mathrm{<mo>\; :\; </mo>}X\to X$ is completely continuous if it is continuous and totally bounded on X. It is clearly that every compact operator is totally bounded, but the converse may not be true, however the two notions are equivalent on bounded subsets of a Banach space X.

Definition 2. [20] A mapping $A\mathrm{<mo>\; :\; </mo>}X\to X$ is called $\mathcal{D}$ -Lipschitzian if there exists a continuous and nondecreasing function ${\varphi }_A\mathrm{<mo>\; :\; </mo>}{ℝ}_{+}\to {ℝ}_{+}$ satisfying

$\Vert Ax-Ay\Vert \le {\varphi }_A\left(\Vert x-y\Vert \right)$

for all $x\mathrm{,\; <mi>\; </mi>}y\in X$ where ${\varphi }_A\left(0\right)=0$ .

Sometimes, we call for the function $\varphi$ to be a D-function of the mapping A on X. In the special case when ${\varphi }_A\left(r\right)=\gamma r,\mathrm{<mi>\; </mi>}\gamma >0$ , A is called a Lipschitz constant $\gamma$ . Obsviously, every Lipschitzian mapping is D-Lipschitzian. In particular if $\gamma <1$ , A is called a contraction with a contraction constant $\gamma$ . Further, if ${\varphi }_A\left(r\right)<r,\mathrm{<mi>\; </mi>}r>0$ then A is called nonlinear contraction on X [20] .

Theorem 1. [20] Let S be a closed convex and bounded subset of a Banach algebra X and let $A\mathrm{<mi>\; </mi>},\mathrm{<mi>\; </mi>}C:S\to X$ be three operators such that:

1) A and C are Lipschitzian with constants $\alpha$ and $\beta$ respectively,

2) B is completely continuous, and,

3) $x=AxBy+Cx\Rightarrow x\in S$ , for all $y\in S$ .

Then the operator equation $AxBx+Cx=x$ has a solution whenever $\alpha M\mathrm{<mi>\; </mi>}+\beta <1$ , where $M=\Vert B\left(S\right)\Vert$ .

3. Main Results

The main object of this section is to apply Theorem 1 to discuss the existence of solutions to the functional quadratic integral Equation (4).

Definition 3. By a solution of the quadratic functional integral Equation (1) We mean a function $x\in ℂ\left(J,ℝ\right)$ that satisfies Equation (1), where $ℂ\left(J,ℝ\right)$ stands for the space of continuous real-valued functions on J.

Consider the following assumptions:

1) $u\mathrm{<mo>\; :\; </mo>\; <mi>\; </mi>}J\times ℝ\mathrm{<mi>\; </mi>}\to \mathrm{<mi>\; </mi>}ℝ$ satisfies Carathéodory condition (i.e. measurable in t for all $x\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}ℝ$ and continuous in x for almost all $t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J$ ). There exist a positive constant k and a function $m\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}{L}^1$ such that:

$\left|u\left(t,x\right)\right|\le m\left(t\right),\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\forall \mathrm{<mi>\; </mi>}\left(t,x\right)\in J\times ℝ$

and ${\displaystyle {\int }_0^b}\frac{1}{t+s}\left|m\left(s\right)\right|\text{d}s\le k.$

2) $f\mathrm{,\; <mi>\; </mi>}g\mathrm{<mo>\; :\; </mo>\; <mi>\; </mi>}J\mathrm{<mi>\; </mi>}\times \mathrm{<mi>\; </mi>}ℝ\mathrm{<mi>\; </mi>}\to ℝ$ are continuous and bounded with $K_1=\underset{\left(t,x\right)\in J\times ℝ}{{\displaystyle \sup }}\left|f\left(t,x\right)\right|$ $K_2=\underset{\left(t,x\right)\in J\times ℝ}{{\displaystyle sup}}\left|g\left(t\mathrm{,}x\right)\right|$ respectively.

3) There exist two positive constants $L_1$ and $L_2$ satisfying

$\left|f\left(t\mathrm{,}x\right)-f\left(t\mathrm{,}y\right)\right|\le L_1\left|x-y\right|$

and

$\left|g\left(t\mathrm{,}x\right)-g\left(t\mathrm{,}y\right)\right|\le L_2\left|x-y\right|$

for all $t\in J$ and $x\mathrm{,\; <mi>\; </mi>}y\in ℝ$ .

4) $\psi \mathrm{<mo>\; :\; </mo>\; <mi>\; </mi>}J\times ℝ\mathrm{<mi>\; </mi>}\to \mathrm{<mi>\; </mi>}ℝ$ is continuous for all $t\in J$ and $x\in ℝ$ . Moreover,

$\underset{\forall t\in J}{{\displaystyle \sup }}\left|\psi \left(t,0\right)\right|=K_3.$

5) There exists a constant $L_3$ satisfying

$\left|\psi \left(t\mathrm{,}x\right)-\psi \left(t\mathrm{,}y\right)\right|\le L_3\mathrm{<mi>\; </mi>}\left|x-y\right|$

for all $t\in J$ and $x\in ℝ$ .

Theorem 2. Let the assumptions 1)-5) be satisfied. Furthermore, if

$L_2\left(K_3+L_3\cdot {\Vert m\Vert }_{L^1}\right)+L_1<1,$ then the quadratic functional integral equation

(1) has at least one solution in the space $ℂ\left(J,ℝ\right)$ .

Proof:

Consider the mapping A, B and C on $ℂ\left(J,ℝ\right)$ , defined by:

$\left(Ax\right)\left(t\right)=g\left(t,x\left(t\right)\right)$

$\left(Bx\right)\left(t\right)=\psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}u\left(s,x\left(s\right)\right)\text{d}s\right)$

$\left(Cx\right)\left(t\right)=f\left(t,x\left(t\right)\right).$

Then functional integral Equation (1) can be written in the form:

$Tx\left(t\right)=Cx\left(t\right)+Ax\left(t\right)\cdot Bx\left(t\right).$ (2)

Hence the existence of solutions of the FIE (1) is equivalent to finding a fixed point to the operator Equation (7) in $ℂ\left(J,ℝ\right)$ . We shall prove that A, B and C satisfy all the conditions of Theorem 1.

Let us define a subset S of $ℂ\left(J,ℝ\right)$ by

$S:=\left\{x\in \mathrm{<mi>\; </mi>}ℂ\left(J,ℝ\right),\Vert x\Vert \le r\right\}.$

Obviously, S is nonempty, bounded, convex and closed subset of $ℂ\left(J,ℝ\right)$ .

For every $x\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}S\mathrm{,}$ since $0<s\Rightarrow t<t+s\Rightarrow \frac{1}{t}>\frac{1}{t+s},$ then $1>\frac{t}{t+s}$ we have

$\left|\left(Tx\right)\left(t\right)\right|=\left|Cx\left(t\right)+Ax\left(t\right)Bx\left(t\right)\right|\mathrm{<mi>\; </mi>}\le \mathrm{<mi>\; </mi>}{K}_1+K_2\left(K_3+L_3\cdot {\Vert m\Vert }_{L^1}\right)=r.$

Then, $Tx\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}S$ and hence $TS\mathrm{<mi>\; </mi>}\subset \mathrm{<mi>\; </mi>}S$ .

First. we start by showing that C is Lipschitzian on S. To see that, let $x\mathrm{,\; <mi>\; </mi>}y\in S\mathrm{.}$ So

$\left|Cx\left(t\right)-Cy\left(t\right)\right|=\left|f\left(t,x\left(t\right)\right)-f\left(t,y\left(t\right)\right)\right|\le L_1\left|x\left(t\right)-y\left(t\right)\right|$

for all $t\in J\mathrm{.}$ Taking supremum over t

$\Vert Cx-Cy\Vert \le L_1\mathrm{<mi>\; </mi>}\Vert x-y\Vert$

for all $x\mathrm{,\; <mi>\; </mi>}y\in S\mathrm{.}$ This shows that C is a Lipschitzian mapping on S with the Lipschitz constant $L_1$ .

By a similar way we can deduce that

$\Vert Ax-Ay\Vert \le L_2\Vert x-y\Vert$

for all $x\mathrm{,\; <mi>\; </mi>}y\in S\mathrm{.}$ This shows that A is a Lipschitzizan mapping on S with the Lipschitz constant $L_2$ .

Secondly, we show that B is continuous and compact operator on S. First we show that B is continuous on S. To do this, let us fix arbitrary $ϵ>0$ and let $\left\{x_n\right\}$ be a sequence of point in S converging to point $x\in S\mathrm{.}$ Then we get

$\begin{array}{l}\left|\left(B{x}_n\right)\left(t\right)-\left(Bx\right)\left(t\right)\right|\\ \le \left|\psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x_n\left(s\right)\right)\text{d}s\right)-\psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x\left(s\right)\right)\text{d}s\right)\right|\\ \le L_3{\displaystyle {\int }_0^t}\frac{t}{t+s}\left|u\left(s,x_n\left(s\right)\right)-u\left(s,x\left(s\right)\right)\right|\text{d}s\\ \le L_3{\displaystyle {\int }_0^t}\frac{t}{t+s}\left[\left|u\left(s,x_n\left(s\right)\right)\right|+\left|u\left(s,x\left(s\right)\right)\right|\right]\text{d}s\\ \le 2L_3{\displaystyle {\int }_0^b}\frac{t}{t+s}m\left(s\right)\text{d}s\le 2L_3{\Vert m\Vert }_{L^1}\le ϵ.\end{array}$

Thus

$\left|\left(B{x}_n\right)\left(t\right)-\left(Bx\right)\left(t\right)\right|\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\mathrm{<mi>\; </mi>}n\to \infty \mathrm{.}$

Furthermore, let us assume that $t\in J\mathrm{.}$ Then, by assumption 4) and Lebesgue dominated convergence theorem, we obtain the estimate:

$\begin{array}{c}\underset{n\to \infty }{\lim }\left(B{x}_n\right)\left(t\right)=\underset{n\to \infty }{\lim }\psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x_n\left(s\right)\right)\text{d}s\right)\\ =\psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x\left(s\right)\right)\text{d}s\right)=\left(Bx\right)\left(t\right)\end{array}$

for all $t\in J\mathrm{.}$ Thus, $B{x}_n\to Bx$ as $n\to \infty$ uniformly on J and hence B is a continuous operator on S into S. Now by 1) and 2)

$\begin{array}{c}\left|B{x}_n\left(t\right)\right|\le \left|\psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x_n\left(s\right)\right)\text{d}s\right)-\psi \left(t,0\right)\right|+\left|\psi \left(t,0\right)\right|\\ \le L_3\left|{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x_n\left(s\right)\right)\text{d}s\right|+K_3\\ \le L_3{\displaystyle {\int }_0^b}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x\left(s\right)\right)\text{d}s+K_3\\ \le K_3+L_3\cdot {\Vert m\Vert }_{L^1}\end{array}$

for all $t\in J\mathrm{.}$ Then $\Vert B{x}_n\left(t\right)\Vert \le \mathrm{<mi>\; </mi>}{K}_3+L_3\cdot {\Vert m\Vert }_{L^1}$ for all $n\in N\mathrm{.}$ This shows that $\left\{B{x}_n\right\}$ is a uniformly bounded sequence in $B\left(S\right)$ .

Now, we proceed to show that it is also equi-continuous. Let $t_1\mathrm{,\; <mi>\; </mi>}{t}_2\in J$ (with- out loss of generality assume that $t_1<t_2$ ), then we have

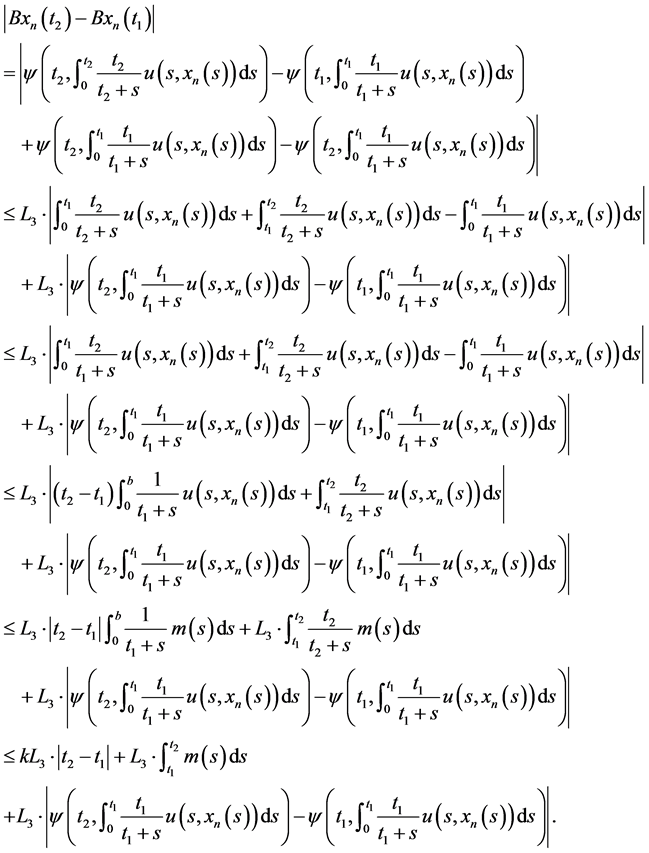
Then, we obtain

$\left|B{x}_n\left(t_2\right)-B{x}_n\left(t_1\right)\right|\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\mathrm{<mi>\; </mi>}{t}_2\to t_1\mathrm{.}$

As a consequence, $\left|B{x}_n\left(t_2\right)-B{x}_n\left(t_1\right)\right|\to 0$ as $t_2\to t_1$ . This shows that $\left\{B{x}_n\right\}$ is an equicontinuous sequence in S. Now an application of Arzela-Ascoli theorem yields that $\left\{B{x}_n\right\}$ has a uniformly convergent subsequence on the the compact subset J. without loss of generality, call the subsequence it self. We can easily show that $\left\{B{x}_n\right\}$ is Cauchy in S.

Hence $B\left(S\right)$ is relatively compact and consequently B is a continuous and compact operator on S.

Since all conditions of Theorem 1 are satisfied, then the operator $T=C+AB$ has a fixed point in S. +

4. Examples and Remarks

In this section, we present some examples and particular cases in nonlinear analysis.

As a particular case of Theorem 2, an existence theorem of solutions to the following quadratic integral equation of Chandrasekhar type

$x\left(t\right)=f\left(t,x\left(t\right)\right)+\mathrm{<mi>\; </mi>}g\left(t,x\left(t\right)\right){\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x\left(s\right)\right)\text{d}s,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J$ (3)

is obtained.

Example 4.1:

As a particular case of Theorem 2 (when $f\left(t,x\right)=1,\mathrm{<mi>\; </mi>}g\left(t,x\right)=x,\mathrm{<mi>\; </mi>}\psi \left(t,x\right)=x$ and $u\left(t,x\right)=\lambda \cdot x\left(t\right)\cdot \varphi \left(t\right)$ , $\lambda$ is positive constant) we can obtain theorem on the existence of solutions belonging to the space $ℂ\left(J,ℝ\right)$ for the quadratic integral equation

$x\left(t\right)=1+x\left(t\right){\displaystyle {\int }_0^t}\frac{t\lambda \varphi \left(s\right)}{t+s}x\left(s\right)\text{d}s,\mathrm{<mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J.$ (4)

The usually existence of solutions of (4) is proved under the additional as- sumption that that the so-called characteristic function $\varphi$ is an even poly- nomial in s [1] .

If $\varphi \mathrm{<mo>\; :\; </mo>\; <mi>\; </mi>}J\to ℝ$ is a function in $L_{\infty }$ and $4\lambda {\Vert \varphi \Vert }_{L_{\infty }}\le 1$ , then the quadratic in- tegral equation (4) has at least one solution in $ℂ\left(J,ℝ\right)$ .

In case of $\lambda =1.$ Then ${\Vert \varphi \Vert }_{L_{\infty }}\le \frac{1}{4}$ and $r\le 4$ . Therefore, the quadratic in-

tegral equation

$x\left(t\right)=1+x\left(t\right){\displaystyle {\int }_0^t}\frac{t\varphi \left(s\right)}{t+s}\mathrm{<mi>\; </mi>}x\left(s\right)\text{d}s\mathrm{,}\mathrm{<mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J\mathrm{,}$

has at least one solution in $\left\{x\left(t\right)\mathrm{<mo>\; |\; </mo>\; <mi>\; </mi>}x\in ℂ\left(J,ℝ\right)\mathrm{<mo>\; :\; </mo>\; <mi>\; </mi>}\Vert x\Vert \le 4\right\}\mathrm{.}$

In our work, we prove the existence of solutions of Equation (4) under much weaker assumptions ( $\varphi$ need not to be continuous).

Example 4.2:

Equation (1) includes the well known functional equation [24]

$x\left(t\right)=f\left(t,x\left(t\right)\right).$

Example 4.3: For $g\left(t,x\right)=1$ Then Equation (1) has reduced to the form

$x\left(t\right)=\psi \left(t,{\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}u\left(s,x\left(s\right)\right)\text{d}s\right),\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J.$

Example 4.4: For $f\left(t,x\right)=a\left(t\right),\mathrm{<mi>\; </mi>}g\left(t,x\right)=x$ and $\psi \left(t,x\right)=x$ Then Equation (1) has the form

$x\left(t\right)=a\left(t\right)+x\left(t\right){\displaystyle {\int }_0^t}\frac{t}{t+s}u\left(s,x\left(s\right)\right)\text{d}s,\mathrm{<mi>\; </mi>}t\in J.$

Example 4.5: Consider the quadratic integral equation

$x\left(t\right)=1+\frac{tx\left(t\right)}{1+\left|x\left(t\right)\right|}{\displaystyle {\int }_0^t}\frac{t}{t+s}\frac{\left|x\left(s\right)\right|}{1+\left|x\left(s\right)\right|}\text{d}s,$ (5)

where $f\left(t,x\right)=1,\mathrm{<mi>\; </mi>}g\left(t,x\left(t\right)\right)=\frac{tx\left(t\right)}{1+\left|x\left(t\right)\right|},\mathrm{<mi>\; </mi>}\psi \left(t,x\left(t\right)\right)=x$ and

$u\left(s,x\left(s\right)\right)=\frac{\left|x\left(s\right)\right|}{1+\left|x\left(s\right)\right|}.$

We can easily verify that $f\mathrm{,\; <mi>\; </mi>}g\mathrm{,\; <mi>\; </mi>}\psi$ and $u$ satisfy all the assumptions of Theorem 2.

5. Further Existence Results

Consider now the quadratic integral equation

$x\left(t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{g}_i\left(t,x\left(t\right)\right)\cdot {\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}{u}_i\left(s,x\left(s\right)\right)\text{d}s,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J=\left[0,b\right].$ (6)

Also, the existence of solutions for the Equation (6) can be proved by a direct application of the following fixed point theorem [25] .

Theorem 3. Let n be a positive integer, and $\mathcal{C}$ be a nonempty, closed, convex and bounded subset of a Banach algebra X. Assume that the operators $A_i\mathrm{<mo>\; :\; </mo>}X\to X$ and $B_i:\mathcal{C}\to X,\mathrm{<mi>\; </mi>}i=1,2,\cdots ,n,$ satisfy

1) For each $i\in \left\{\mathrm{1,2,}\cdots \mathrm{,}n\right\}$ , $A_i$ is D- Lipschitzian with a D-function ${\varphi }_i$ ;

2) For each $i\in \left\{\mathrm{1,2,}\cdots \mathrm{,}n\right\}$ , $B_i$ is continuous and $B_i\left(\mathcal{C}\right)$ is precompact;

3) For each $y\in \mathcal{C}$ , $x={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{A}_{i}x\cdot B_{i}y$ implies that $x\in \mathcal{C}$ .

Then, the operator equation $x={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{A}_{i}x\cdot B_{i}x$ has a solution provided that

${\displaystyle \underset{i=1}{\overset{n}{\sum }}}{M}_i{\varphi }_i\left(r\right)<r,\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\forall r>0,$

where $M_i=\underset{x\in \mathcal{C}}{{\displaystyle \sup }}\Vert B_{i}x\Vert ,\mathrm{<mi>\; </mi>}i=1,2,\cdots ,n.$

Equation (6) is investigated under the assumptions:

1) $u_i:\mathrm{<mi>\; </mi>}J\times ℝ\mathrm{<mi>\; </mi>}\to \mathrm{<mi>\; </mi>}ℝ,\mathrm{<mi>\; </mi>}i=1,2,\cdots ,n$ satisfy Carathéodory condition (i.e. measurable in t for all $x\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}ℝ$ and continuous in x for almost all $t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J$ ) such that:

$\left|u_i\left(t,x\right)\right|\le m_i\left(t\right)\in L^1,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}i=1,2,\cdots ,n\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\forall \mathrm{<mi>\; </mi>}\left(t,x\right)\in J\times ℝ$

and $k_i=\underset{t\in J}{{\displaystyle \sup }}{\displaystyle {\int }_0^b}\frac{1}{t+s}\mathrm{<mi>\; </mi>}{m}_i\left(s\right)\text{d}s$ for all $i=1,2,\cdots ,n$ such that $k_i\ne 0\forall i.$

2) $g_i:\mathrm{<mi>\; </mi>}J\mathrm{<mi>\; </mi>}\times \mathrm{<mi>\; </mi>}ℝ\mathrm{<mi>\; </mi>}\to ℝ,\mathrm{<mi>\; </mi>}i=1,2,\cdots ,n$ are continuous and bounded

with $h_i=\underset{\left(t,x\right)\in J\times ℝ}{{\displaystyle \sup }}\left|g_i\left(t,x\right)\right|,\mathrm{<mi>\; </mi>}i=1,2,\cdots ,n.$

3) There exist constants $L_i,i=1,2,\cdots ,n$ satisfying

$\left|g_i\left(t,x\right)-g_i\left(t,y\right)\right|\le L_i\left|x-y\right|,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}i=1,2,\cdots ,n$

for all $t\in J$ and $x\mathrm{,\; <mi>\; </mi>}y\in ℝ\mathrm{.}$

Theorem 4. Let the assumptions 1)-3) be satisfied. Furthermore, if

${\displaystyle \underset{i=1}{\overset{n}{\sum }}}\left(h_i-L_i\right)k_i>0,$ then the general quadratic integral equation

(6) has at least one solution in the space $ℂ\left(J,ℝ\right)$ .

Proof:

Consider the mapping $A_i$ and $B_i$ on $ℂ\left(J,ℝ\right)$ defined by:

$\left(A_{i}x\right)\left(t\right)=g_i\left(t,x\left(t\right)\right)$

$\left(B_{i}x\right)\left(t\right)={\displaystyle {\int }_0^t}\frac{t}{t+s}{u}_i\left(s,x\left(s\right)\right)\text{d}s.$

Then the integral Equation (6) can be written in the form:

$Tx\left(t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{A}_{i}x\left(t\right)\cdot B_{i}x\left(t\right)$ (7)

we shall show that $A_i$ and $B_i$ satisfy all the conditions of Theorem 3.

Let us define a subset $\mathcal{C}$ of $ℂ\left(J,ℝ\right)$ by

$\mathcal{C}:=\left\{x\in ℂ\left(J,ℝ\right),\mathrm{<mi>\; </mi>}\Vert x\Vert \le r\right\}.$

Obviously, $\mathcal{C}$ is nonempty, bounded, convex and closed subset of $ℂ\left(J,ℝ\right)$ .

As done before in the proof of Theorem 2 we can get, For every $x\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}\mathcal{C}$ we have

$\left(Tx\right)\left(t\right)\le b{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{h}_i{k}_i=r.$

Then, $Tx\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}\mathcal{C}$ and hence $T\mathcal{C}\mathrm{<mi>\; </mi>}\subset \mathrm{<mi>\; </mi>}\mathcal{C}$ .

Easily, we can deduce that

$\Vert A_{i}x-A_{i}y\Vert \le L_i\Vert x-y\Vert$

for all $x\mathrm{,\; <mi>\; </mi>}y\in \mathcal{C}\mathrm{.}$ This shows that $A_i$ are a Lipschitz mapping on $\mathcal{C}$ with the Lipschitz constants $L_i$ . Also, we can prove that the operators $B_i$ are con- tinuous and compact operator on $\mathcal{C}$ for all $t\in J$ and $\Vert B_{i}x\left(t\right)\Vert \le b{k}_i=M_i$ for all $x\in \mathcal{C}$ .

Since all conditions of Theorem 3 are satisfied, then the operator $T={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{A}_i\cdot B_i$

has a fixed point in $\mathcal{C}$ . +

As particular cases of Theorem 4 we can obtain theorems on the existence of solutions belonging to the space $ℂ\left(J,ℝ\right)$ for the following integral equations:

1) Let $n=1$ , then we have

$x\left(t\right)=g_1\left(t,x\left(t\right)\right)\cdot {\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}{u}_1\left(s,x\left(s\right)\right)\text{d}s,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J.$

2) Let $n=1$ with $g_1\left(t,x\left(t\right)\right)=1,$ then we have

$x\left(t\right)={\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}{u}_1\left(s,x\left(s\right)\right)\text{d}s,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}t\mathrm{<mi>\; </mi>}\in \mathrm{<mi>\; </mi>}J.$

3) Let $n=2$ , then we have

$x\left(t\right)=g_1\left(t,x\left(t\right)\right)\cdot {\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}{u}_1\left(s,x\left(s\right)\right)\text{d}s\mathrm{<mi>\; </mi>}+\mathrm{<mi>\; </mi>}{g}_2\left(t,x\left(t\right)\right)\cdot {\displaystyle {\int }_0^t}\frac{t}{t+s}\mathrm{<mi>\; </mi>}{u}_2\left(s,x\left(s\right)\right)\text{d}s,\mathrm{<mi>\; </mi>}t\in J.$

4) $x\left(t\right)=x\left(t\right)\cdot {\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\displaystyle {\int }_0^t}\frac{{\lambda }_i\mathrm{<mi>\; </mi>}t}{t+s}\mathrm{<mi>\; </mi>}{\varphi }_i\left(s\right)x\left(s\right)\text{d}s,\mathrm{<mi>\; </mi>}t\in J$

where ${\varphi }_i:\mathrm{<mi>\; </mi>}J\to ℝ,\mathrm{<mi>\; </mi>}i=1,2,\cdots ,n$ are functions in $L_{\infty }$ and ${\lambda }_i,\mathrm{<mi>\; </mi>}i=1,2,\cdots ,n$ are positive constants.

5) Let $n=2,$ then we have

$x\left(t\right)=x\left(t\right)\cdot {\displaystyle {\int }_0^t}\frac{{\lambda }_{1}t}{t+s}{\varphi }_1\left(s\right)x\left(s\right)\text{d}s\mathrm{<mi>\; </mi>}+\mathrm{<mi>\; </mi>}x\left(t\right)\cdot {\displaystyle {\int }_0^t}\frac{{\lambda }_{2}t}{t+s}{\varphi }_2\left(s\right)x\left(s\right)\text{d}s,\mathrm{<mi>\; </mi>}t\in J$

${\varphi }_i:\mathrm{<mi>\; </mi>}J\to ℝ,\mathrm{<mi>\; </mi>}i=1,2$ are two functions in $L_{\infty }$ and ${\lambda }_i,\mathrm{<mi>\; </mi>}i=1,2$ are positive con- stants.

6. Conclusion

In this paper, we proved an existence theorem for some functional-integral equations which includes many key integral and functional equations that arise in nonlinear analysis and its applications. In particular, we extend the class of characteristic functions appearing in Chandrasekhar’s classical integral equation from astrophysics and retain existence of its solutions. Finally, some examples and remarks were illustrated.

Acknowledgements

The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, on the material support for this research under the number (2915) during the academic year 1436 AH/2015 AD.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Chandrasekhar, S. (1960) Radiative Transfer. Dover, New York.
[2]	Argyros, I.K. (1985) Quadratic Equations and Applications to Chandrasekhar’s and Related Equations. Bulletin of the Australian Mathematical Society, 32, 275-292. https://doi.org/10.1017/S0004972700009953
[3]	Cichoń, M. and Metwali, M.M.A. (2016) On a Fixed Point Theorem for the Product of Operators. Journal of Fixed Point Theory and Applications, 18, 753-770. https://doi.org/10.1007/s11784-016-0319-7
[4]	Dhage, B.C., Salunkhe, S.N., Agarwal, R.P. and Zhang, W. (2005) A Functional Differential Equation in Banach Algebras. Mathematical Inequalities & Applications, 8, 89-99. https://doi.org/10.7153/mia-08-09
[5]	El-Sayed, A.M.A. and Hashem, H.H.G. (2010) Monotonic Positive Solution of a Nonlinear Quadratic Functional Integral Equation. Applied Mathematics and Computation, 216, 2576-2580.
[6]	El-Sayed, A.M.A. and Hashem, H.H.G. (2013) Existence Results for Nonlinear Quadratic Integral Equations of Fractional Order in Banach Algebra. Fractional Calculus and Applied Analysis (FCAA), 16, 816-826. https://doi.org/10.2478/s13540-013-0051-6
[7]	Banas, J., Lecko, M. and El-Sayed, W.G. (1998) Existence Theorems of Some Quadratic Integral Equation. Journal of Mathematical Analysis and Applications, 227, 276-279.
[8]	Caballero, J., Mingarelli, A.B. and Sadarangani, K. (2006) Existence of Solutions of an Integral Equation of Chandrasekhar Type in the Theory of Radiative Transfer. Electronic Journal of Differential Equations, 2006, 1-11.
[9]	El-Sayed, W.G. and Rzepka, B. (2006) Nondecreasing Solutions of a Quadratic Integral Equation of Urysohn Type. Computers & Mathematics with Applications, 51, 1065-1074.
[10]	Subramanyam, P.V. and Sundarsanam, S.K. (1996) A Note on Functional Integral Equations. Differential Equations and Dynamical Systems, 4, 473-478.
[11]	Ntouyas, S.K. and Tsamatos, P.G. (1999) A Fixed Point Theorem of Krasnoselskii-Nonlinear Alternative Type with Applications to Functional Integral Equations. Differential Equations and Dynamical Systems, 7, 139-146.
[12]	Dhage, B.C. and O’Regan, D. (2000) A Fixed Point Theorem in Banach Algebras with Applications to Functional Integral Equations. Functional Differential Equations, 7, 259-267.
[13]	Dhage, B.C. (1994) On α-Condensing Mappings in Banach Algebras. The Mathematics Student, 6, 146-152.
[14]	Dhage, B.C. (2006) On Some Nonlinear Alternatives of Leray-Schauder Type and Functional Integral Equations. Archivum Mathematicum, 42, 11-23.
[15]	Banas, J. and Sadarangani, K. (2003) Solutions of Some Functional-Integral Equations in Banach Algebra. Mathematical and Computer Modelling, 38, 245-250.
[16]	Dhage, B.C. (1988) On Some Variants of Schauder’s Fixed Point Principle and Applications to Nonlinear Integral Equations. Journal of Mathematical and Physical Sciences, 22, 603-611.
[17]	Banas, J. and Lecko, M. (2002) Fixed Points of the Product of Operators in Banach Algebras. Panamerican Mathematical Journal, 12, 101-109.
[18]	Dhage, B.C. (2005) On a Fixed Point Theorem in Banach Algebras with Applications. Applied Mathematics Letters, 18, 273-280.
[19]	Dhage, B.C. (2004) Local Fixed Point Theory Involving Three Operators in Banach Algebras. Topological Methods in Nonlinear Analysis, 24, 377-386.
[20]	Dhage, B.C. (2001) On Existence Theorems for Nonlinear Integral Equations in Banach Algebras via Fixed Point Technique. East Asian Mathematical Journal, 17, 33-45.
[21]	Dhage, B.C. (1987) A Fixed Point Theorem and Application to Nonlinear Integral Equations. Proceeding of International Symposium in Nonlinear Analysis, Applications and Bio-Mathematics, Waltair, India, 53-59.
[22]	Dhage, B.C. (2004) A Fixed Point Theorem in Banach Algebras Involving Three Operators with Applications. Kyungpook Mathematical Journal, 44, 145-155.
[23]	Argyros, I.K. (1992) On a Class of Quadratic Integral Equations with Perturbations. Functiones et Approximatio, 20, 51-63.
[24]	Kuczma, M. (1968) Functional Equations in a Single Variable. PWN, Warsaw.
[25]	Long, W., Zheng, X.-J. and Li, L. (2012) Existence of Periodic Solutions for a Class of Functional Integral Equations. Electronic Journal of Qualitative Theory of Differential Equations, 57, 1-11.