1. Introduction
Recently, Escher and Yin [1] studied the following nonlinear dispersive equation (b-equation):
(1.1)
where
,
,
and
are arbitrary real constants. Denoting
, we can rewrite b-equation in the following form:
(1.2)
Equation (1.2) can be derived as a family of asymptotically equivalent shallow water wave equations that emerge at quadratic order accuracy for
by an appropriate Kodama transformation [2] [3] . For the case
, the corresponding Kodama transformation is singular and the asymptotic ordering is violated [2] [3] . The solutions of the b-Equation (1.2) with
were studied numerically for various values of b in [4] [5] , where b was taken as a bifurcation parameter. The symmetry condition necessary for integrability of the b-Equation (1.2) was investigated in [6] . The Korteweg-de Vries (KdV) equation, the Camassa-Holm (CH) equation and the Degasperis-Procesi (DP) equation are the only three integrable equations in the b-Equation (1.2), which was shown in [7] [8] by using Painleve analysis. The b-equation with
admits peaked solutions for
[4] [5] [7] . The peaked solutions replicate a feature that is characteristic for the waves of great height: waves of the largest amplitude that are exact solutions of the governing equations for water waves [9] [10] [11] .
If
and
, then b-Equation (1.1) becomes the well-known KdV equation
(1.3)
which describes the unidirectional propagation of waves at the free surface of shallow water under the influence of gravity [12] . In this model,
re- presents the wave’s height above a flat bottom; x is proportional to distance in the direction of propagation and t is proportional to the elapsed time. The KdV equation is completely integrable, and its solitary waves are solitons [13] . The Cauchy problem of the KdV equation has been studied by many authors [14] [15] [16] and a satisfactory local or global (in time) existence theory is now available (for example, in [15] [16] ). The solution of the KdV equation is global for
[15] [16] . It is also observed that the KdV equation does not accommodate wave breaking (by wave breaking we mean the phenomenon that a wave remains bounded but its slope becomes unbounded in finite time) [17] .
For
and
, b-Equation (1.1) becomes the CH equation
(1.4)
modelling the unidirectional propagation of shallow water waves over a flat bottom. Again
stands for the fluid velocity at time t in the spatial x direction and
is a nonnegative parameter related to the critical shallow water speed [18] . The CH equation is derived physically by approximating directly the Hamiltonian for Euler’s equations in the shallow water regime (it also appears in the context of hereditary symmetries studied by Fuchssteiner and Fokas [19] ). Recently, the alternative derivations of the CH equation as a model for water waves, respectively, as the equation for geodesic flow on the diffeomorphism group of the circle were presented in [20] and in [21] . For the physical derivation, we refer to the work in [22] . The geometric interpretation is important because it can be used to prove that the least action principle holds for the CH equation [23] . It is worth pointing out that the fundamental aspect of the CH equation, the fact that it is a completely integrable system, was shown in [24] [25] for the periodic case and in [26] [27] for the non-periodic case. Its solitary waves are smooth if
and peaked in the limiting case
[28] . They are orbitally stable and interact like solitons [29] [30] and the explicit interaction of the peaked solitons is given in [14] .
Since the CH equation is structurally very rich, many physicists and mathematicians pay great attention to it. Local well-posedness for the initial datum
with
was proved by several authors, as in [31] [32] [33] [34] . For the initial data with lower regularity, we refer to Molinet’s paper [35] and also the paper [36] . Moreover, wave breaking for a large class of initial data has been established in [31] [33] [37] [38] . However, in [39] , global existence of weak solutions was proved but uniqueness was obtained only under a prior assumption that is known to hold only for the initial data
such that
is a sign-definite Radon measure (under this condition, global existence and uniqueness was shown in [40] ). Also it is worth noting that CH equation has global conservative solutions in
[36] [41] [42] and global dissipative solutions (with energy being lost when wave breaking occurs) in
[43] [44] . In [45] , the authors showed the infinite propagation speed for the CH equation in the sense that a strong solution of the Cauchy problem with compact initial profile cannot be compactly supported at any later time unless it is the zero solution, which is an improvement of the previous results in this direction obtained in [46] .
For
and
in b-Equation (1.1), then we find the DP equation of the form [8]
(1.5)
Degasperis, Holm and Hone [47] proved the formal integrability of the DP Equation (1.5) by constructing a Lax pair. They also showed that DP equation has a bi-Hamiltonian structure and an infinite sequence of conserved quantities, and that it admits exact peakon solutions which are analogous to the CH peakons. Peakons for either b = 2 or b = 3 are true solitons that interact via elastic collisions under CH dynamics, or DP dynamics, respectively. Recently, Lundmark [48] showed that the DP equation has not only peaked solitons, but also shock peakons of the form
The DP equation can be regarded as a model for nonlinear shallow water dynamics and its asymptotic accuracy is the same as for the CH shallow water equation [2] [3] [22] . An inverse scattering approach for computing n-peakon solutions to the DP equation was presented in [49] . Its traveling wave solutions were investigated in [50] .
The Cauchy problem for the DP equation has been studied widely. Local well-posedness of this equation is established in [51] [52] for the initial data
with
. Similar to the CH equation, the DP equation has also global strong solutions [51] [53] [54] [55] as well as finite time blow-up solutions [51] [53] [54] [56] [57] . On the other hand, it has global weak solutions in
[53] [56] [58] . Analogous to the case of the CH equation, Henry [59] and Mustafa [60] showed that smooth solutions to the DP equation have infinite speed of propagation. Coclite and Karlsen [61] also obtained global existence results for entropy weak solutions belonging to the class of
and the class of
.
Although the DP equation is similar to the CH equation in several aspects, these two equations are truly different. One of the novel features of the DP equation different from the CH equation is that it has not only peakon solutions [47] and periodic peakon solutions [58] , but also shock peakons [48] [61] and the periodic shock waves [56] .
Despite the abundant literature on the above three special cases of the b-equ- ation, there are few results on the b-equation. Recently, some authors devoted to studying the Cauchy problem of the b-equation. Since the conservation laws of the b-equation are much weaker, there are only a few kinds of global or blow-up results.
In [1] , Escher and Yin studied b-equation on the line for
and
. They established the local well-posedness, described the precise blow-up scenario, and proved that the equation has strong solutions which exist globally in time and blow up in finite time. Moreover, the authors showed the uniqueness and existence of global weak solutions to b-equation, provided the initial data satisfy certain sign conditions. The similar discussions for b-equation on the circle can be found in [62] . The author expanded the result of corresponding solutions blow-up in finite time where conditions on the initial data and the bifurcation parameter
in [2] to the case
[63] . In [64] , the authors established the local well-posedness for the nonuniform weakly dissipative b-equation which includes both the weakly dissipative CH equation and the weakly dissipative DP equation as its special cases. They studied the blow-up phenomena and the long time behavior of the solutions.
Recently Gui, Liu, and Tian [65] considered b-Equation (1.1) with
on the real line. They proved that the equation is locally well-posed in the Sobolev space
for
. Moreover, they give the precise blow-up scenario of strong solution of the equation with certain initial data. In [66] , Zhou established blow-up results for b-equation with
under various classes of initial data. He also proved that the solutions with compact support initial data do not have compact support. In the periodic case of b-equation with
, sufficient conditions on the initial data were obtained in [67] to guarantee the finite time blow-up and global existence. The local well-posedness of b-equation with
in the critical Besov space
was studied in [68] . They showed that if a weaker
-topology is used, the solution map becomes Hölder continuous. Moreover, they showed that the dependence on initial data is optimal in
in the sense that the solution map is continuous but not uniformly continuous. They also obtained the periodic peaked solutions and applied them to obtain the ill-posedness in
. There are some other papers concerned with b-equation of
and we will not attempt to mention all here.
In the past decades, the optimal control of distributed parameter systems has become much more active in academic field. Especially, the optimal control of nonlinear solitary wave equation lies in the front of the intersection of mathematics, engineering and computer science and so on. Recently, people have taken a considerable interest in realizing the operation mechanism of prototype tsunami in the laboratory and in looking for a really efficient control mechanism to generate exact long water waves in the man-made pool. The CH equation attracted much more attention also in the context of the relevance of integrable equations to the modelling of tsunami waves [69] [70] [71] . Naturally, an optimization problem needs to be considered in this shallow water wave equation. It seems to the author that the study of nonlinear shallow water equation from the point of view of control theory was an open field. There are only some research results reported. For instance, Zhang studied the control problems for two nonlinear dispersive wave equations--the KdV equation and the Benjamin-Bona- Mahony (BBM) equation. Moreover, for the BBM equation, he showed that the wave-maker, by choosing a proper boundary value, can make a wave to approach a given state as closely as desired as long as the given state is small in some sense [72] . Glass investigated the problem of exact controllability and asymptotic stabilization of the CH equation on the circle, by means of a distributed control. The results are global, and in particular the control prevents the solution from blowing up [73] . The distributed optimal control problems for the viscous CH equation, the viscous DP equation, the viscous Dullin-Gottwald- Holm (DGH) equation were considered by our research team respectively. We proved the existence and uniqueness of weak solution in short interval. Further, we employed the quadratic cost objective functional to be minimized within an admissible control set with the distributive observation and discussed the existence of optimal control which minimizes the quadratic cost functional [74] [75] [76] . Subsequently, by the Dubovitskii-Milyutin functional analytical approach, Sun considered the optimal distributed control problem of the viscous generalized CH equation and viscous DGH equation respectively and obtained the Pontryagin maximum principle of the systems studied. The necessary optimality condition is established for an optimal control problem in fixed final horizon case [77] [78] . In [79] [80] , recently, our research team studied optimal distributed control of the Fornberg-Whitham equation and the θ-equation which involve complex nonlinear items respectively. We clarified the well-posedness of weak solution without relying on viscous coefficient, which is major improvement in comparison with our previous results. Utilizing the Dubovitskii- Milyutin functional analytical approach, we also proved the necessary optimality condition for the control systems in fixed final horizon case. Hwang studied the quadratic cost optimal control problems for the viscous DGH equation. He derived the necessary optimality conditions of optimal controls, corresponding to physically meaningful distributive observations. By making use of the second order Gateaux differentiability of solution mapping on control variables, he also proved the local uniqueness of optimal control [81] .
Inspired by the papers mentioned above, in present work, we investigate the b-equation from the point of view of distributed control. More precisely, we consider the following governing equation
(1.6)
where
is the external control term which is L-periodic in spatial x, 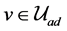 is a control and B be an operator called a controller. The explicit formulation of the control problem will be provided after the investigation of well-posedness of the state equation.
is a control and B be an operator called a controller. The explicit formulation of the control problem will be provided after the investigation of well-posedness of the state equation.
We mainly consider the two following problems:
・ for the nonlinear control system governed by the b-equation with quadratic cost functional
, can one find
such that
and whether this
is unique?
・ if one finds the unique optimal control
for the above control problem, how can we characterize this optimal control?
The plan of the remaining sections can be summarized as follows. In Section 2, we study the initial-boundary problem of the b-equation with forcing function in a special space
. Adopting the Faedo-Galerkin method and utilizing a uniformly prior estimate of the approximate solution, we prove the existence and uniqueness of weak solution under the definition introduced in the paper. For general
, the proof without relying on viscous coefficient is a major improvement in comparison with our results in [74] [75] [76] and other discussions in [77] [78] [81] . In Section 3, based on the well-posedness result, we give the formulation of the quadratic cost optimal control problem for the b-equation and investigate the existence and uniqueness of the optimal solution. In Section 4, by the method of control theory (for more detailed discussion, we refer readers to book [82] ), we establish the sufficient and necessary optimality condition of an optimal control in fixed final horizon case. In order to obtain this result, we also prove the Gateaux differentiability of the state variable
which is used to define the associate adjoint systems. Comparing with the research in our previous works [74] [75] [76] and the related works [77] [78] [79] [80] [81] , the sufficient and necessary optimality condition of an optimal control which is not limited to the necessary condition is another novelty in this paper. At last, in Section 5, we give the specific sufficient and necessary optimality condition of optimal control
for two physical meaningful distributed observation cases employing the associate adjoint systems.
2. The Existence and Uniqueness of Weak Solution
Without loss of generality, we assume
. Denote the usual Hilbert
space
equipped with the norm
, and the inner
product in H is denoted by
. Let
,
be the integral exponent Sobolev spaces. By using the Poincare’s inequality in
, we can define norm
, where
and
. Especially, taking
, we get the Hilbert space
supplied with the inner product
, where
. Let us denote that
and
are the dual spaces of V and H respectively. Then we can find that V embeds into H and
embeds into
, where each embedding is dense and corresponding injections are continuous.
For convenience, we shall consider the following initial-boundary value problem for Equation (1.1)
(2.1)
where
is forcing item which is L-periodic in spatial x.
With
and
, Equation (2.1) takes the form:
(2.2)
In order to study the weak solution of Equation (2.2), we introduce the following two special spaces firstly.
is defined by
, which is equipped with the norm
.
is defined by
endowed with the norm
.
It is easy to verify that the spaces
and
are both Hilbert spaces.
Definition 2.1. A function
is said to be a weak solution of Equation (2.2), if
satisfies
(2.3)
for
in the sense of
.
From now on, when we speak of a solution of Equation (2.2), we shall always mean the weak solution in the sense of Definition 2.1 unless noted otherwise.
We set an unbounded linear self-adjoint operator
, where
Math_106#. Then the set of all linearly independent
eigenvectors
of A with the eigenvalues
, i.e.,
,
as
,
is an orthonormal basis of H.
Furthermore, we can define the powers
of A for
, where the space
is a Hilbert space which is endowed with the norm
. It can be found that the following expression holds
,
where
are eigenvectors of
and
are eigenvalues.
Definition 2.2. A function
is called
an approximate solution to Equation (2.2), if it satisfies
(2.4)
where
,
and
.
Lemma 2.1. Let
and
satisfies the boundary conditions of Equation (2.1). Then, we get
,
where
is a constant.
The proof of Lemma 2.1 can be referred to our article [79] [80] .
Theorem 2.1. Assume that
and
. Then, Equation (2.2) exhibits a unique weak solution
.
Proof: Multiplying both sides of the first equation in Equation (2.4) by
and summing up over j from 1 to m, we have
This gives
. (2.5)
Because
is a forcing function, we can assume that
, where
is constant.
It then derives from Equation (2.5) that
, (2.6)
where
are embedding constants. In order to estimate the term
, we should estimate the term
in
.
Multiplying both sides of the first equation in Equation (2.4) by
and summing up over j from 1 to m, we get
The above equation implies that
(2.7)
By the use of the Sobolev embedding theorem, we can estimate the following items as
;
and
,
where
are embedding constants.
Therefore, we can deduce from Equation (2.7) that
where
. (2.8)
From inequality (2.8), we can obtain that
(2.9)
where
,
and
is a constant.
Therefore, combining the boundedness of the sequence
in
with the inequality (2.6), we can derive that
(2.10)
where
,
and
is some positive constant.
Similarly, multiplying both sides of the first equation in Equation (2.4) by
and summing up over j from 1 to m, we can get
By integration by parts in the above equation, we can deduce that
(2.11)
Using the Sobolev embedding theorem, inequality (2.9) and boundary conditions of Equation (2.4), we can estimate the following each item
and
.
Combining above estimates, Equation (2.11) can be deduced into the following inequality
(2.12)
From inequality (2.12), we can obtain that
(2.13)
where
,
and
is a constant.
Hence, combining estimate inequality (2.9) and (2.13), we can find that
, (2.14)
which indicate
. We also can have
from the fact of V embeds into H.
Combining estimate inequality (2.9) and (2.10), we also can know that
. (2.15)
Therefore, we deduce from inequality (2.14) that
, (2.16)
which indicates
is uniformly bounded in
.
Afterward, we will prove uniform boundedness of sequence
in
. Indeed, from the first equation of Equation (2.2) and the Sobolev embedding theorem, we have
(2.17)
where
are embedding constants as before.
It derives from inequality (2.17) that
Collecting the analysis above, one has:
(I) For
, where
,
the sequence
is bounded in
as well as in
, which is independent of the dimension of ansatz space
.
(II) For
, where
,
the sequence
is bounded in
, which is also independent of the dimension of ansatz space
.
So, we obtain the boundedness of
in
from (I) and (II) mentioned above. By the extraction theorem of Rellich’s, there may extract a subsequence
of
and find a
such that
in
, as
. (2.18)
Utilizing the fact that V embeds H compactly and (2.18), we can refer to the conclusion of Aubin-Lions-Teman’s compact embedding theorem to verify that
is pre-compact in
. Hence we can choose a subsequence (denoted again by
) of
such that
in
, as
. (2.19)
Because
embeds into
, we can obtain that
Math_214#. Then, by virtue of (2.19), we can find a subsequence (denoted again by
) of
such that
in
, as
, for
a.e.. (2.20)
Combining (2.18)-(2.20) and the Lebesgue dominated convergence theorem, we have
in
, as
; (2.21)
in
, as
; (2.22)
in
, as
. (2.23)
We replace
and
by
and
respectively in the first equation of Equation (2.4), which yields
(2.24)
Multiplying both sides of Equation (2.24) by
, where
,
and integrating the result equation over
, we have
(2.25)
Utilizing (2.19), (2.21)-(2.23), we may pass to the limit in Equation (2.25). Then, we get
(2.26)
We can find Equation (2.26) is true for any
. Therefore, we may take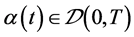 , then Equation (2.26) gives
, then Equation (2.26) gives
in the sense of
.
Since j is arbitrary and finite linear combinations of
is dense in H, we can find that
satisfies Definition 2.1. Hence, from complex analysis above and Lemma 2.1, we obtain the existence of weak solution
Math_248# to Equation (2.2).
Next we will discuss the uniqueness of this weak solution.
Let
and
be any two weak solutions of Equation (2.1) and set
. Then
satisfies
(2.27)
Taking the inner product of both sides of the first equation in Equation (2.27) with
, we obtain
(2.28)
The right hand side of Equation (2.28) can be estimated as follows:
;
;
,
where
is an embedding constant and
are some con- stants.
Combining all complex estimates above and Equation (2.28), we can deduce that
, (2.29)
where
Integrating inequality (2.29) with respect to t over
, we have
, (2.30)
where
. It follows from
that
, which implies
.
This completes the proof of uniqueness.
3. The Existence and Uniqueness of an Optimal Control
In this section, we will give the formulation of the quadratic cost optimal control problem for b-equation and investigate the existence and uniqueness of an optimal solution.
Let
be a Hilbert space of control variables, and
be an operator called a controller. We assume that the admissible set
be a bounded closed convex set, which has the non-empty interior with respect to
topology, i.e.
.
We study the following nonlinear control system:
(3.1)
where
is a control. By virtue of Theorem 2.1 and Equation (3.1), we can uniquely define the solution mapping
of
into
. The weak solution
is called the state variable of the nonlinear control system (3.1).
The observation of the state is assumed to be given by
, (3.2)
where
is an operator called the observer and
is a Hilbert space of the observation variables.
We shall consider the following quadratic cost functional associated with the nonlinear control system (3.1):
, (3.3)
where
is a desired value of
.
is symmetric and positive definite, i.e.,
, where
is some constant.
Hence, the discussed optimal control problem is to find an element
such that
,
which subject to the controlled system (3.1) together with the control constraints.
Now, we shall discuss the existence and uniqueness of an optimal control
for the cost functional (3.3), which is the content of the following theorem.
Theorem 3.1. Let us suppose that the hypotheses of Theorem 2.1 are satisfied. Then there exists a unique optimal control
for the nonlinear control
system (3.1) with the cost functional (3.3), such that
.
Proof. Because
is a closed convex set, there exists a minimizing sequence
in
such that
.
We set
and
.
Then cost functional (3.3) can be rewritten as
, (3.4)
where
is a continuous symmetric bilinear form on
and
is a continuous linear form on
.
Obviously,
is bounded in
. So, the quadratic cost functional (3.3) implies that there exists a constant
such that
, (3.5)
which indicates that
is bounded in
. Because
is closed and convex set, we can extract a subsequence
and find a
such that
in
, as
. (3.6)
From now on, each state variable
corresponding to
is the solution of
(3.7)
where
.
From inequality (3.5), the right hand side of the first equation in Equation (3.7) can be estimated as
, (3.8)
where
is some constant.
Utilizing inequality (3.8), we can apply the same method used in Theorem 2.1 to deduce that
is bounded in
. Hence, by the extraction theorem of Rellich’s, we can extract a subsequence
of
and find a
such that
in
, as
. (3.9)
Using the fact that V embeds H compactly and the result of (3.9), we can refer to the conclusion of Aubin-Lions-Teman’s compact embedding theorem to verify that
is pre-compact in
. So we can also choose a subsequence (denoted again by
) of
such that
, in
as
. (3.10)
On the other hand, because
embeds into
, we can infer that
. And from (3.10), we can get a subsequence (denoted again by
) of
such that
in
, as
, for
a.e.. (3.11)
Combining (3.9)-(3.11) and the Lebesgue dominated convergence theorem, it is not difficult to obtain that
in
, as
; (3.12)
in
, as
; (3.13)
in
, as
; (3.14)
in
, as
. (3.15)
We replace
and
by
and
in Equation (3.7) respectively, and take
. Then, by the standard arguments as in [83] , we find that the limit u satisfies the following equations:
(3.16)
in weak sense, where
. Moreover, by the uniqueness of weak solution of Equation (3.16) via Theorem 2.1 and Lemma 2.1, we can conclude that
Math_371#, which implies
in
.
Because the mapping
is lower semi-continuous in the weak topology of
and
is also lower semi-continuous. The mapping
is continuous in the weak topology of
. Thus the mapping
is weakly lower semi-continuous.
So, we can deduce from cost functional (3.4) that
. (3.17)
At the same time, from inequality (3.17), we have
.
Moreover, combining
by definition, we can obtain that
. (3.18)
Next, we will prove the uniqueness of
in (3.18).
Because the mapping
is strictly convex and the mapping
is continuous. Hence the mapping
is also strictly convex.
Let
and
be two optimal controls, which satisfy
and
respectively. Because
is a bounded closed convex set, we can get that
. We thus can deduce that
, which is a contradiction unless
. This completes the proof.
From the above analysis, we can conclude that
of
is a unique optimal solution to the optimal control problem investigated.
4. The Sufficient and Necessary Optimality Condition
In this section, we shall characterize the optimal control by giving the sufficient and necessary condition for optimality. We firstly give the following lemma according to optimal control theory.
Lemma 4.1. Assume that the mapping
is differentiable, strictly convex and
is bounded. Then the unique element (optimal control)
in
satisfying
can be characterized by
, (4.1)
where
and
denote the derivative of
at
.
Proof. Let
be the optimal control subject to Theorem 3.1. Then for
and
, we have
. (4.2)
From inequality (4.2), we can derive that
. (4.3)
Therefore, if we pass to the limit in inequality (4.3), we obtain that
, where
.
Alternatively, suppose inequality (4.1) remains true. Because the mapping
is strictly convex, we can get
, for
. (4.4)
From inequality (4.4), we deduce that
. (4.5)
If we pass the limit in inequality (4.5), we can get
,
for
, which completes the proof.
Conditions of the type (4.1) are usually termed as “first order sufficient and necessary condition”, in terminology of calculus of variations. In order to analyze inequality (4.1), we need to prove that the mapping
of
is differentiable at
.
Definition 4.1. The solution mapping
of
into
is said to be differentiable at
in any direction w, if for
and
, there exists a
such that
in
, as
.
The function
is called the directional derivative of
, which plays crucial in the following discussion.
Theorem 4.1. The mapping
of
into
is derivative at
and such the derivative of
at
in the direction
, say
, is a weak solution of the following equation:
(4.6)
where
and
.
Proof. Let
. We set
and
. Then
satisfies
(4.7)
where
.
In order to estimate
, we multiply both sides of the first equation in Equation (4.7) by
and integrate it over
. Then we get
(4.8)
Each item on the right hand of Equation (4.8) can be estimated as follows:
;
;
and
,
where
is an embedding constant and
are some constants.
Hence, Equation (4.8) can be changed into
, (4.9)
where
.
It follows from inequality (4.9) and the Gronwall’s lemma that
(4.10)
where
.
Next, multiplying both sides of the first equation in Equation (4.7) by
and integrating it over
, which gives
(4.11)
Then, we estimate the each item of the right hand of Equation (4.11) as follows:
;
;
and
where
is an embedding constant and
are some constants.
By the above estimates, we can deduce from Equation (4.11) that
, (4.12)
where
.
Applying Gronwall’s lemma to inequality (4.12), which yields
(4.13)
where
.
Similarly, multiplying both sides of the first equation in Equation (4.7) by
and integrating it over
, which gives
(4.14)
We can also estimate each item of the right hand of Equation (4.14) as follows:
;
;
;
;
and
,
where
are some constants and
are some embedding constants.
Combining a series of complex estimates above and Equation (4.14), we can obtain that
, (4.15)
where
.
By applying the Gronwall’s lemma to inequality (4.15), we can get
(4.16)
where
.
Combining estimate inequality (4.13) and (4.16), we can deduce that
. (4.17)
Similarly, combining estimate inequality (4.10) and (4.13), we can obtain that
. (4.18)
From inequality (4.17), we derive that
, (4.19)
which indicates a uniformly
bounded of
.
Afterward, we will prove a uniformly
bounded of
.
From the first equation in Equation (4.7) and the Sobolev embedding theorem, we have
(4.20)
where
are some embedding constants and
are some constants.
Analogously, from inequality (4.20), we can get
(4.21)
Combining inequality (4.19) and (4.21), we can establish the boundedness of
in
. Hence, from Lemma 2.1, we can deduce that
.
From now on, we can infer that there exists a
and a sequence
tending to 0 such that
in
, as
. (4.22)
Because the imbedding
into
is compact, then it can deduce from (4.22) that
in
a.e.
, (4.23)
for some
tending to 0 as
. Whence by (4.22) - (4.23), Theorem 2.1 and the Lebesgue dominated convergence theorem, we can easily obtain that
in
; (4.24)
in
; (4.25)
in
; (4.26)
in
; (4.27)
as
, where
. And also we can derive from Equation (4.7) and inequality (4.21) that
in
, as
. (4.28)
Therefore, we can infer from (4.24) to (4.28) that
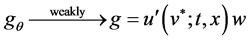
in
as
in which g is a solution of Equation (4.6).
Consequently, the solution mapping
of
into
is differentiable in the weak topology of
. This completes the proof.
The conclusion of Theorem 4.1 means that the cost
is derivative at
in the direction
. So, we can get that
Then the sufficient and necessary optimality condition (4.1) can be rewritten as
(4.29)
for , where
is the canonical isomorphism
onto
and
is desired value.
, where
is the canonical isomorphism
onto
and
is desired value.
5. The Two Cases of Distributive Observations
In this section, we will characterize the optimal control by giving the sufficient and necessary optimality condition (4.29) for the following two cases of physical meaningful observations:
(I) We set
and
, then observe that
.
(II) We set
and
, then observe that
.
Firstly, we discuss the cost functional expressed by
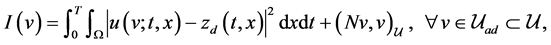 (5.1)
(5.1)
where
is a desired value. Let
be the optimal control subject to Equation (3.1) and cost functional (5.1). Then the sufficient and necessary optimality condition (4.29) can be represented by
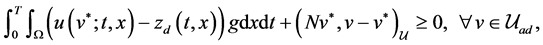 (5.2)
(5.2)
where
is the weak solution of Equation (4.6). Now we will introduce the adjoint system to describe the optimality condition (5.2):
(5.3)
where
and
.
Therefore, we can provide the characterization for the optimal control
of the quadratic cost functional (5.1) as follows:
Theorem 5.1. The optimal control
of the quadratic cost functional (5.1) is characterized by the following control system, adjoint system and inequality:
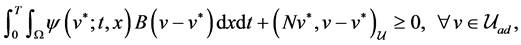
where
and
.
Proof. Taking inner product of the first equation in Equation (5.3) by g over
, then integrating the result equation with respect to t on
, we get
(5.4)
Combining Equation (4.6) and Equation (5.3) and taking integration by parts, the left hand side of Equation (5.4) yields
(5.5)
where
. Therefore, utilizing Equation (5.4) and Equation (5.5), the sufficient and necessary optimality condition (5.2) is equivalent to
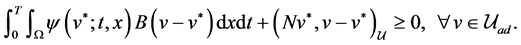
Hence, the theorem is proved.
Secondly, we discuss the cost functional expressed by
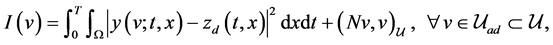 (5.6)
(5.6)
where
is a desired value. Let
be the optimal control subject to Equation (3.1) and cost functional (5.6). Then the sufficient and necessary optimality condition (4.29) is represented by
 (5.7)
(5.7)
where
and
is the weak solution of Equation (4.6). Similarly, we formulate the adjoint system to describe the optimality condition (5.7):
(5.8)
where
and
.
Hence, we can give the following theorem.
Theorem 5.2. The optimal control
of the quadratic cost functional (5.7) is characterized by the following control system, adjoint system and inequality:
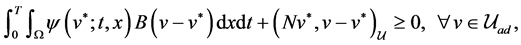
where
and
.
Proof. As we did before, we multiply both sides of the first equation of Equation (5.8) by g and integrate it over
. Then we have
(5.9)
where
.
Utilizing Equation (4.6), the integration by parts on the left hand side of Equation (5.9) yields
(5.10)
where
. Therefore, combining Equation (5.9) and Equation (5.10), the sufficient and necessary optimality condition (5.7) is equivalent to
,  ,
,
which completes the proof.
6. Conclusions
b-equation is an important shallow water wave equation which has many practical meanings. In this paper, we aim at pursuing an in-depth study of the optimal control issue of the classical b-equation. So, we investigate firstly the local existence and uniqueness of solution to the initial-boundary problem of the b-equation with source term, and then discuss the formulation of the quadratic cost optimal control problem for the b-equation, obtain the existence and uniqueness of an optimal control, establish the sufficient and necessary optimality condition of an optimal control in fixed final horizon case. Moreover, we give the specific sufficient and necessary optimality condition for two physical meaningful distributive observation cases by employing associate adjoint systems. Compared with other papers in similar directions, the weak solution analysis of b-equation without relying on viscous item is one technical innovation, and the sufficient and necessary optimality condition of an optimal control which is not limited to the necessary condition is another novelty. However, much work remains to be done in this direction. For example, it is an optimal control problem of the distributed parameter system governed by the nonlinear partial differential equation, to obtain the numerical solutions for the optimal control-trajectory pair is not an easy job due to the tremendous calculation and possible model difficulties. We try to finish this non-trivial work in the follow-up research by optimizing numerical algorithm and carrying out numerical simulation, which can provide a basis for application in the engineering field.
Acknowledgements
Research was supported in part by the National Natural Science Foundation of China (No: 11371175, 11501253, 11571140).