A Combined Heterotic String and Kähler Manifold Elucidation of Ordinary Energy, Dark Matter, Olbers’s Paradox and Pure Dark Energy Density of the Cosmos ()
1. Introduction
Since we believe that understanding the frame of mind of the author of a paper is very beneficial to understanding the paper itself, we decided to start with two general remarks which are not specifically related to the paper being of a very general nature but never the less the author had an almost compelling feeling to get these scientific remarks off his chest right from the start.
The first remark is that without scepticism no scientific progress is possible. That is because it would not be possible to challenge old, established and believed theories. The present author, being a follower of a host of sceptical philosophers, starting from the great David Hume understands this very well. On the other hand absolute scepticism must ultimately lead to a paralysis of all innovations and discoveries. In our modest opinion the right scientific attitude of the prospective reader of the present paper is to tread this narrow path between the above mentioned two extremes and give the author the benefit of the doubt.
The second remark maybe deeply related to the first and is essentially linked to the secret of why we think we have succeeded in the present work where so many admittedly much better scientists have not succeeded. Our intrinsically biased answer is the golden mean number system, which is the basis of our computation. To understand this, the following analogy may be rather instructive and insightful, suppose for a moment that European scientists at the beginning of the age enlightenment did not accept Leonardo of Pisa (alias Fibonacci) proposal to take over the Arabic ciphers and particularly their use of the Indian zero. It is not particularly difficult to see that sticking to the Roman numerals and ignoring the role of the zero would have required many centuries more to be able to solve that way integral differential equations. Clearly numbers systems and notations could make all the difference here. It is our contention and deep belief that similar reasoning holds for the use of the gold mean system in high energy physics and quantum cosmology and to liken the progress brought to science by adopting the Arabic numerics and methods of computation to that of using the golden mean system in E-infinity theory is not an exaggeration [55] .
It is not unusual for unexpected, experimental discovery, observation or measurement in physics and cosmology to cause havoc in our long established and time honoured theories and send us into a state of partial minor or major period of perplexity [1] - [22] . When such events happen we tend more often than not to overestimate the difficulties created by this new situation [20-24]. Sensational headlines of popular scientific press and writing may also add to the perceived mysteries and increase the degree of fogginess. On the positive side, and as stressed by A. Whitehead, a major contradiction in science is also a new opportunity for a greater understanding that prompts young and older scientists to rise to the new challenge and question old dogmas and possibly conventionally accepted wrong theories [3] [4] [12] [24] . There is little doubt that the discovery of accelerated cosmic expansion and the missing mass as well as energy, dubbed dark energy of the cosmos [23] [25] - [41] falls into the category of truly major upheavals in physics and cosmology based on accurate measurements and modern observations, some of which earned several Nobel Prizes in physics [25] - [42] .
The present work takes the view that our current mathematical knowledge and general theories [3] [9] [11] [40] are in position to explain ordinary energy, dark matter and pure dark energy both qualitatively and quantitatively [25] - [46] . We are furthermore of the optimistic view that our new understanding of these unexpected measurements and observations have actually helped to reduce the number of mysteries rather than increase them [28] . This is the case particularly when we look upon the expansive antigravity force causing accelerated expansion as the global form of the local attractive Casimir effect as it accumulates at the boundary of the universe [35] . Similarly dark energy turned out to be the kinetic energy of the supposedly energyless quantum probability wave while ordinary energy is basically the potential energy of the quantum particle [26] [30] . Nothing could be more assuring for this conclusion than the fact that adding this kinetic wave energy to this potential particle energy one finds a total potential energy which is identical to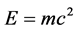 
maximal energy equation of Einstein’s special relativity with a new interpretative twist for being not only the recipe of converting matter into energy but also as being the maximal energy density of the universe [26] [27] .
In what follows we give several simple computations attesting to the above and will combine Einstein’s geometry [22] [24] [27] with the field theoretical structure and topology of Heterotic string theory [19] [45] [47] [48] to show how the special relativistic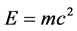 
could be decomposed into three different quantum components, namely that of ordinary energy density
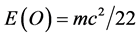, dark matter energy density 
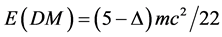and pure dark energy density
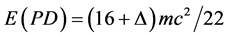. Here 
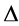is a small coupling constant estimated at approximately 
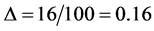which cancels out for the total maximal energy 
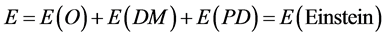[32] . It is needless to say that the 22 in the preceding equation may be interpreted in various intimately connected ways. It could be seen first as simply the 26 maximal dimensions of the heterotic string theory [49] minus Einstein’s four spacetime dimensions implicit in his 
[42] [51] . Second, and deep down equivalently, the 22 could be seen as a measure of the ruggedness, i.e. fractal non- smoothness of a K3 Kähler manifold as compared with Einstein’s spacetime for which the corresponding number is unity [53] [54] . Note also that the three energy components amount to a density of approximately 4 percent, 22 percent and 74 percent respectively in outstanding agreement with the overwhelming modern cosmic measurements [18] [25] - [32] . A particularly important feature of the present analysis is the near perfect similarity of the end result with that based on the geometry and topology of a Kerr black hole, which gives our 22 an indirect third interpretation [32] . In addition we point out something similar played by the so called redundant components of the Riemannian tensor [37] [51] . To see all of that in some detail is one of the main the tasks of the following sections where the exact value and derivation of the 
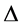coupling will also be given [25] - [51] . In addition we have cited the most important background reading on set theory and noncommutative geometry in physics because both are indispensible for a deep understanding of the present paper [52] - [59] . We even went as far as summoning our civil scientific courage to propose that the present theory could be viewed as a transfinite version of the cellular automata’s interpretation of quantum mechanics as advocated recently by no one less than Gerard ‘tHooft who is one of a handful of architects of modern high energy physics [60] . It is also a Cantorian version of Arend Niehaus’ Zitterbewegung model [61] of quantum physics without quantum mechanics as well as a justification of attributing dark energy to Olbers’s paradox of the dark night sky [62] .
2. Prologue
Very deep down at the roots, the present work is a scientific interrogation of the role played by contradiction between theory, experiments and observations in the development of physics and cosmology [1] - [25] . However the thinking underpinning the methodology of the solution may have started by the author asking himself why L. Hardy’s exact solution of quantum entanglement was found using Dirac’s bra and ket and leading to the golden mean to the power of five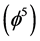 
[25] - [30] . Why was it not any other formulation of quantum mechanics? We will answer this question at the end of the present paper in section No. 10.
Starting from Einstein’s famous energy equation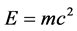
, interpreted as the maximal energy density in the cosmos [18] [22] [42] , we utilize the mathematical structure and the corresponding physical meaning of the Heterotic superstring theory to understand and quantify ordinary energy, dark matter and pure dark energy density of the cosmos [25] - [48] . In particular it is shown that while measurable ordinary dark energy is connected to the classical ordinary photon 
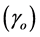and dark matter is essentially due to five degrees of freedom which may be three massive relatives of the classical
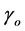, namely 
as well as the Higgs H and the graviton g, we posit that the carriers of pure dark energy are the 16 extra bosons of Heterotic string theory [19] [24] [47] [49] [50] . Recalling that these extra bosons are moving in the opposite direction to the fundamental ten spacetime dimensions of the heterotic superstrings, it comes as no surprise that this feature of the present elucidation is most valuable for understanding the observed puzzling phenomenon of accelerated cosmic expansion which would normally imply a negative kind of gravity [30] [46] [51] . In fact in the counter intuitive higher dimensionality of D = 26 and D = 10, a negative sign of a topological quantity such as the signature will most definitely have a physical consequence such as accelerated expansion due to a repulsive gravity. Summarizing the preceding pint in a single equation we can simply state that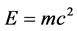 
may be seen as the sum of three parts. The first part is the ordinary energy
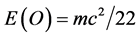, the second part is the dark matter energy density 
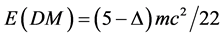and the third part is the pure dark energy density![]()
, where m is the mass, c is the speed of light, ![]()
is the weak coupling between dark matter and pure dark energy and the devisor 22 is the sum of 1 + 5 + 16 explained earlier on and interpreted as the various degrees of freedom [28] - [38] . We conclude by noting the existence of an almost one to one correspondence between the geometry and topology imposed on spacetime by Heterotic string theory structure and the geometry and topology of a K3 Kähler manifold with its negative signature ![]()
being equal to Gross’ 16 extra dimensions as well as a Kerr black hole which leads to identical three parts dissection of the maximal energy density of the cosmos [32] . Similar conclusions are also obtained via the redundant components of the Riemann tensor as well as Dvoretzky’s theorem [36] [39] . We may draw the attention of the reader from the outset to the subtle fact that a most fundamental point in the present work is that we do make a sharp distinction between zero, empty and insubstantial nothingness as done in the seminal work of A. Connes [56] [57] . We said from the outset that we start our analysis with Einstein’s![]()
. This central point is however far from being trivial. In fact and as stressed for instance by W. Rindler, this equation must be taken as an axiom rather than something that can be derived from first principles [58] . Similarly our use of ![]()
as the maximal energy density in the universe will be taken in the present work also as an axiom for simplicity as well as clarity [26] [27] . The present work takes these results as far as reasoning that the Zitterbewegung [61] may be seen as a spiralling random Cantor set quantum path with a Hausdorff dimension equal to ![]()
where ![]()
is the golden mean as well as uncovering the fractal spacetime connection between dark energy and Olbers’s paradox dark sky [62] .
3. Dvoretzky’s Theorem as a Bird’s Eye View of Dark Energy
One of the most remarkable theorems in higher dimensional geometry asserts that in a manifold of sufficiently high dimensionality, most of the volume is concentrated very near to the surface [36] [39] . This is essentially the quintessence of Dvoretzky’s theorem [36] . More precisely for a five dimensional ball such as the Kaluza-Klein theory, 96 percent of the volume is at a narrow layer near to the surface. This leaves only 4 percent for the ordinary space volume [36] . The situation is clearly analogous to that of a zero set quantum particle surrounded by an empty set quantum wave [37] [38] where the volume and consequently the energy of the quantum particle turned out to be ![]()
while the volume-energy of the quantum wave is ![]()
where ![]()
[32] - [42] . Inserting for ![]()
we find that the “topological” volume of the quantum particle is 4.5% of the total unit volume while that of the quantum wave is 95.5% [37] [38] . This squares perfectly with the mathematics of Dvoretzky’s theorem as well as with the physics of dark energy as explained in far more details on previous occasions [27] [36] . Next we will move from this global view to more specific computation as we will also be showing how the approximately 96% dark energy is subdivided into 22% dark matter and 74% pure dark energy [29] - [44] . It is also extremely important in the present context to stress again and draw attention to the remarkable almost perfect similarity between the three part dissection of energy in the present analysis using the heterotic superstring theory and its K3 Kähler manifold [53] [54] and the same result obtained via the geometry and topology of a Kerr black hole [32] . This similarity seems to suggest that the geometry and topology imposed on spacetime via the 16 extra bosonic dimensions of Heterotic string theory may have deep relations to the geometry and topology of a spinning Kerr black hole and the signature ![]()
of our K3 ![]()
Kähler manifold [32] [53] [54] which seems to warrant separate careful further investigation.
4. Ordinary Energy and Dark Energy Density from the Independent and the Redundant Components of the Riemannian Tensor and the Heterotic String Theory
It is well known that the number of components of the driving force behind Einstein’s general relativity, i.e. the Riemannian tensor in four dimensions is given by [22] [52]
![]()
(1)
However the linearly independent components are only 20 given by [24] [25]
![]()
(2)
Pondering this situation one has to consider the possibility that the 256 are not redundant but may play the role of the empty set quantum wave and could be the carrier of dark energy in a non-trivial way [26] [33] - [40] . This initial vague thought can be made more physical and precise when linked to the Heterotic string theory of Gross and his team [19] . Let us recall that each extra bosonic string of the 16 extra bosons has 16 bosonic fields. The total is consequently
![]()
(3)
mirroring the total number of Riemannian components in four dimensions [19] [24] . In addition we have here the two fundamental deceptively trivial equations of Heterotic strings which combine the dimensionality of the Veneziano-Nambu strong interaction bosonic strings model D = 26 with the Green-Schwarz type II superstrings with D = 10, namely [19] [49]
![]()
(4)
as well as
![]()
(5)
where ![]()
is Einstein’s spacetime dimensionality [26] [45] [46] [47] [48] [49] . In the above we have tacitly assumed the reader to be familiar with the toroidal compactification of the 16 D. Gross extra bosonic dimensions [19] [47] as well as the Calabi-Yau compactification of the 6 dimensions in the D = 10 superstring theory [19] [50] . Putting all that together it becomes obvious that the total number of particle-like objects involved is 256 minus the 6 compactified dimensions, i.e. 250 [51] . Now it is elementary guesswork to see that the density, which is nearest to our notion of ordinary energy, must be given by [29] - [42]
![]()
(6)
This is trivially similar to dividing the photon ![]()
by the 1 + 5 + 16 = 22 bosonic degrees of freedom left from the maximal 26 after subtracting D = 4 of Einstein. In other words, we eliminated the compactified “things” from their corresponding total and determined the relevant ratio which turns out to reinforce the picture afforded by Dvoretzky’s theorem [36] and the zero set quantum particle inside the empty set quantum wave as discussed in detail in previous publications [37] . To determine the dark energy density from the above is of course equally trivial and is found from the following self explanatory equation to be [29] - [42]
![]()
(7)
as expected. We admit however that the preceding reasoning may be too delicate to go by it alone without a clear-cut argument and we promise to do just that in the coming sections. However before doing so we just like to look first at the problem of subdividing ![]()
into pure dark energy and dark matter. To arrive at pure dark energy density we have to extract from the ![]()
of ![]()
the Kaluza-Klein topological two branes states in eleven dimensions which may be found from Witten’s model to be 55 [25] . This is thus ![]()
so that the pure dark energy density becomes [29] - [42]
![]()
(8)
Consequently we have for dark matter the experimentally and theoretically by now well established value [25] - [42]
![]()
(9)
From the above we see clearly that when it comes to dark energy, the redundant components of the Riemannian tensor, which we traditionally eliminate via symmetry considerations, are not so redundant [58] [59] .
5. The Three Types of Energy Densities of the Cosmos from a Normed Dimensionality for the Universe
The following calculation which may be called natural and miraculous in the same breath is based upon what we think is the most fundamental renormalization-like equation involving all the fundamental coupling constants in a single unification form [43] [44] . This equation is actually the exact reconstruction equation of the famous inverse Sommerfeld fine structure constant of electromagnetism ![]()
where ![]()
and ![]()
is Hardy’s exact value of quantum entanglement [28] . This remarkable equation reads [43] [44]
![]()
(10)
where![]()
, ![]()
, ![]()
, ![]()
and ![]()
[43] . The above values are exact theoretical values. They are very close to the value found for the electroweak scale as far![]()
, ![]()
and ![]()
as are concerned. However ![]()
of the strong interaction and ![]()
of the Planck mass are found from theoretical considerations [45] - [49] . Setting the corresponding value in this equation, one finds ![]()
as expected so that the relation between the E8E8 exceptional Lie symmetry group [19] and ![]()
is found to be a golden mean scaling, namely [29] [43]
![]()
(11)
where ![]()
is ‘tHooft’s renormalon [25] [42] . Here ![]()
is the famous Hardy quantum entanglement probability and k is ‘tHooft’s hypothetical renormalon particle [25] . Now we are in a position to state that the corresponding space dimension is the following normed value representing the sum of all involved inverse coupling constants. This means [26] [43]
![]()
(12)
Looking back on the preceding calculation and looking in the same way forwards to find the subdivision of D(normed) = 100 with respect to the three fundamental components of energy density, we may draw on the largest bosonic dimension of heterotic string theory, namely D = 26 and think of it as made of the 4 relatively “visible” dimensions of Einstein’s spacetime plus 22 not so “visible” dimensions and claim that the following partitioning seems rather logical to put it modestly [26] [40]
![]()
(13)
It is also logical to look upon the 74 dimensions as least “visible” compared to the “visible” 4 of Einstein or the slightly less visible 22 compactified dimensions of Nambu [14] . It is remarkable but no coincident that 4, 22 and 74 corresponds to the 4% ordinary energy density, 22% corresponds to dark matter energy density and 74% is the pure dark energy density [25] - [40] . One thing the author learned from Nobel Laureate Gerardus ‘tHooft is that one should not invoke or believe in miracles in science and should distrust miraculous things [11] . That is surely correct but we note parenthetically that the present miracle only appears as a miracle, however taking all the empirical facts and all previous theoretical analysis into account, this miracle reveals itself as a natural one, namely that of maximal simplicity. It is bordering on a miracle but it is a scientific one based almost exclusively on the fact that the golden mean number system constitutes basically a transfinite Turing machine, i.e. a golden mean super computer as explained elsewhere in greater detail [40] [46] [48] . In this sense we can go on much further than that and claim that the present theory is basically a transfinite cellular automata interpretation of quantum mechanics, a subject about which G. ‘tHooft has written many influential papers [60] .
6. Energy as Eigenvalue and the Standard Model 12 Bosons
The great A. Einstein did not derive ![]()
from a Lagrangian [22] . In addition he never accepted quantum mechanics and naturally never thought about energy as the eigenvalue of a quantum mechanical equation as P. Dirac did for instance [11] [22] . On the other hand we already stated that ![]()
is for us here far more than an equation for converting mass into energy but rather much more general than that, namely as the maximal energy density possible in nature. Now this is not fancy technicalities and has serious consequences for the following reasons [1] .
Suppose Einstein had written a Lagrangian to derive![]()
. This Lagrangian would have had a single degree of freedom, namely the photon [29] which was the only messenger particle known at the time when Einstein conceived his special theory of relativity [22] [26] [29] . Meantime we know that there is not only one messenger particle but also eleven more photon-like messenger particles included in the standard model [22] . In other words, Einstein’s hypothetical Lagrangian is constraining the system far more than it is in reality. Such constraint results in over estimation of any Eigenvalue, i.e. in this case the energy as per a well known theorem due to Lord Rayleigh [22] . Rather than writing a Lagrangian with 12 degrees of freedom to improve on Einstein’s result, we use here a scaling manoeuvre. Considering the elementary fact that the difference between Newton’s kinetic energy ![]()
and Einstein’s energy ![]()
is basically that ![]()
which is a very large constant leading to a scaling factor of ![]()
being replaced by unity , we conjecture that a similarity exponent based on the ![]()
degrees of freedom not included in Einstein’s hypothetical Lagrangian can be used to down scale E as follows [29] [42] :
![]()
(14)
This is almost the same result found from painstaking cosmic measurements [18] and in agreement with all our previous analysis of the ordinary dark energy presented in the preceding sections as well as previous publications using a plethora of different methods based on physical as well as mathematical arguments [25] - [42] . In the next section we will see how the preceding formula can be generalized for pure dark energy as well as the dark matter density of the cosmos [32] .
7. From the Sixteen Extra Heterotic Strings to Pure Dark Energy and Dark Matter Density
Let us look closely at the last equation. The important number there is 22 which, as mentioned repeatedly before, may be seen as the dimensions left after subtracting the needed four spacetime dimensions of Einstein from the maximal dimensions D = 26 of heterotic string theory [45] [46] [47] [48] [49] . Now the only massless photon ![]()
may be seen as the carrier of the measurable ordinary energy with a density equal to one divided by twenty two [25] - [49] . This is a forceful self evident picture both physically and numerically [25] - [49] . In this sense we may regard the 22 left bosonic strings as being the sum of one ordinary photon ![]()
given by U(1) Lie symmetry group plus five more bosons, namely the three massive photon-like messenger particles ![]()
given by the generators of SU(2) as well as one Higgs spin zero boson H to give ![]()
and ![]()
their mass in addition to one graviton g to mediate gravity [22] . Added together this gives us five degrees of freedom reminiscent of the five Kaluza-Klein dimensions in some ways. Finally, and most importantly, we have the 16 D. Gross extra bosonic dimensions, which has a different sign to the 26 of Nambu [14] and the 10 of Green-Schwarz strings, namely [19]
![]()
(15)
i.e.
![]()
(16)
The total number of bosonic degrees of freedom is thus 1 + 5 + 16 = 22 as should be. There is here an extremely subtle twist because unlike the original theory of Gross, where it turns out that the corresponding extra sixteen boson dimensions have all what it takes to cover the need for the gluon and the electroweak which we account for in the present work via SU(2), i.e. ![]()
[22] but we do not include in the present theory SU(3) of the standard model explicitly [22] . Thus in our version of heterotic strings the number of bosons becomes 1 + (3 + 2) + 16 = 22 bosons irrespective of the negative sign of the corresponding 16 extra dimensions [45] - [49] . The negative sign is needed only to account for the repulsive energy simulating anti-gravity, i.e. pure dark energy via the 16 extra dimensions as we repeatedly mentioned above [45] - [49] . We also stress once more before it slips our minds that the maximal 26 dimensions is simply the sum of the preceding 22 plus the four Einstein spacetime dimensions. Putting all these pieces together we see that Einstein’s ![]()
can be rewritten as follows [32] :
![]()
(16)
That way we have a very good approximation for:
(a) Ordinary measurable energy [25] - [48]
![]()
(17)
(b) Dark matter not directly observed energy density [32]
![]()
(18)
and finally:
(c) Pure dark energy density which cannot be measured by any of the presently available technology but can be inferred from the observed accelerated cosmic expansion [32]
![]()
(19)
We note on passing that the same result is obtained from Witten’s five Branes in eleven dimensions using the self explanatory quotients [25] [26] ![]()
. A considerable improvement on the above solution may be obtained when taking the physically obvious weak coupling between pure dark energy and dark matter because both are dark and essentially obtained via the topological volume of the quantum wave empty set [49] . This coupling, which cancels out in the final total sum, is given approximately by the ratio of the extra heterotic strings, i.e. 16 to the total normed dimensions, i.e. 100 and will be denoted by![]()
. Proceeding in this manner one finds that E(O) remains the same but we have [32]
![]()
(20)
while for pure dark energy the density becomes [32]
![]()
(21)
The preceding result may be made exact by including all transfinite corrections. That means since 26 is replaced by ![]()
[24] [26] [41] [48] we have replaced 22 with ![]()
and 16 is replaced with ![]()
where ![]()
is ‘tHooft’s renormalon [25] given by twice the value of Hardy’s quantum probability of entanglement ![]()
or equivalently by ![]()
where ![]()
is the golden mean ![]()
and ![]()
is the Hausdorff dimension of the cobordism of the empty set ![]()
or equivalently the inverse value of the Hausdorff dimension of the core of Cantorian spacetime![]()
, i.e. ![]()
[25] - [48] . Proceeding that way we find the exact value of the ordinary energy density [25] - [48]
![]()
(22)
To find the corresponding E(PD) exact transfinite value we have to replace ![]()
by the exact value, namely ![]()
and find that [40]
![]()
(23)
Finally the exact energy density of dark matter energy is found to be [42]
![]()
(24)
To see the symphonic number theoretical harmony implicit and explicit in the above calculation, it is sufficient to do the following computation with E8E8 on a pocket calculator and see that ![]()
is exactly equal ![]()
. It is also delightful to see how the closed form E(D) and closed form E(O) add together to give the exact density of Einstein’s ![]()
namely [41] [42]
![]()
(25)
In conclusion of this section we may recall that ![]()
is the multiplicative correlated volume of a five dimensional zero set which models the quantum particle in a Kaluza-Klein space D = 5 [37] . By contrast ![]()
is the additive non-corre- lated five dimensional empty set which models the quantum wave in the same D = 5 space [37] - [42] . Since non-correlation and quantum wave behaviour precludes ordinary measurement due to quantum wave collapse, dark energy and dark matter cannot be measured directly unless we can construct quantum waves nondemolition measurement devices as pointed out in various previous publications [25] - [48] . Some readers may find that the very close similarity between the geometry and topology imposed on spacetime by the heterotic 16 extra bosonic dimensions and the geometry and topology of a Kerr black hole with its three energy space regions as well as the K3 Kähler signature being also ![]()
to be a highly instructive subject that warrants separate careful further investigation as we pointed out earlier on [24] - [48] .
8. The Importance of Being Vague and the Various Interpretations of (22) and (−16) in the Analysis of the Dark Section of the Cosmos
Oliver Cromwell used to say a few good men are better than numbers, however in science numbers and number systems are crucial [55] . In the present analysis it is not possible to cover up this fact and pretend that the vital D = 4 of Einstein, D = 26 of Nambu and ![]()
of Gross are incidental whether they are regarded as number mystics or number theory. The fact is that without ![]()
and ![]()
as well as Kaluza-Klein ![]()
we could not have any of the preceding theories. However equally crucial is the importance of being fuzzy or vague in dealing with these numbers and regarding them as being topological dimensions or the number of fundamental bosons or computational indices relevant to the homology of certain manifold as we will argue in the present pre-final section. The present section may as well be termed in praise of being vague. Let us regress and recall the vital topological details of a K3 Kähler manifold [53] [54] . As is well known and discussed previously in many publications, a K3 Kähler is accurately described by [53] [54] :
a. The Betti numbers
![]()
(26)
b. The Hodge numbers
![]()
(27)
c. The Euler characteristic is
![]()
(28)
d. The signature is
![]()
(29)
e. In the case of E-infinity fuzzy K3 Kähler manifold and using the technique of transfinite correction motivated by earlier work by American mathematician F. John, we conclude that
![]()
(30)
and ![]()
and consequently 22 goes to ![]()
where![]()
, ![]()
is the fundamental hypothetical particle named rightly after ‘tHooft’s dimensional renormalization method, ‘tHooft renormalon. Remembering that for the Betti numbers for crisp compact 7 manifolds with ![]()
holonomy, there are 252 different sets of Betti numbers, we see that fuzziness comes naturally to K3 Kähler and it therefore fits perfectly in noncommutative geometry as well as E-infinity theory and the present wok [53] [54] .
From the preceding delicate arguments and subtle connections we conjecture that the extra 16 dimensions of D. Gross insight may be equated to the signature of K3 Kähler while the compactified 22 dimensions of the bosonic sector of the heterotic strings may be seen in a fuzzy light as being the ruggedness-fractal index ![]()
of a K3 Kähler. Recalling that for Einstein’s smooth manifold we have ![]()
we may write the following conclusion which is in full harmony with the entire present analysis [53] [54]
![]()
(31)
for ordinary energy density. Then we have for dark matter energy density [53] [54]
![]()
(32)
Last but not least, we have
![]()
(33)
for pure dark energy with its anti-gravity-like effect. This, together with all the identical previous analysis and conclusions, wraps up our subject nicely [53] [54] . In conclusion of this section it may be in order to combine pure mathematics with intuitive physical understanding of why the signature ![]()
of our K3 Kähler plays an almost identical role to that of D. Gross 16 extra bosonic dimensions. To explain the point we start by noting that it was the renowned French mathematician Rene Thom who showed that the signature of a manifold is a cobordism invariant. Consequently we could think of it as the outer surface of the quantum wave which in turn is the out surface of the quantum particle [37] . Thus it must be the purely one sided Mobius-like expansive border. In a simplistic terminology we have several concentric circular regions. The most inner one is where we have the ordinary energy residing and amounting to the one divided by 22 factors![]()
. Around this there is the five Kaluza-Klein region leading to the ![]()
factor of dark matter energy density. Finally the border of the ![]()
region is the 16 objects region leading to the factor ![]()
of pure dark energy density of the cosmos. Since there is nothing after that, it follows that there is no counter topological pressure there to balance the ![]()
and consequently we have an implied negative sign as manifests in the signature of K3 Kähler and it is our present conjecture that this is the rationale behind the observed accelerated cosmic expansion of our universe [33] - [40] .
9. General Conclusions
Einstein’s iconic equation ![]()
is interpreted in the present work as the maximal energy density possible obtainable from a corresponding hypothetical maximally restricted one degree of freedom Lagrangian where the classical photon ![]()
is mathematically and physically the said only degree of freedom in a four dimensional spacetime [29] . On the other hand pondering the U(1) SU(2) SU(3) standard model [11] [22] [23] [24] and adding the new insight gained from the Higgs physics, quantum gravity and in particular the remarkable heterotic superstring theory with its 16 extra bosonic strings, we are lead to a triadic dissection of![]()
, namely an ordinary energy density, a dark matter energy density and a pure dark energy density. In particular it is shown that the pure dark energy density is carried by the extra 16 bosonic dimensions of the heterotic strings discovered by D. Gross and his team. Thus starting from the heterotic D = 26 and substituting the Einstein spacetime stage dimensions D = 4, we subdivide the remaining ![]()
corresponding to the three spacetime regions of a Kerr black hole geometry [32] . The first part is connected to the classical photon and leads to the measurable ordinary energy density ![]()
with the quasi Lorentzian factor ![]()
replacing Einstein’s maximal Lorentzian-like factor![]()
. The second and third groups by contrast are weakly coupled. Thus from ![]()
we see that the second five elements group leads to the dark matter energy density ![]()
where ![]()
while the third sixteen elements group leads to the pure dark energy density![]()
. Recalling that the sum E(DM) + E(PD) gives the energy density of the quantum wave [37] [38] it becomes clear that without using wave nondemolition measurement devices the dark sector could not be directly quantified experimentally. Furthermore it is clear that because pure dark energy density is directly related to the extra 16 bosonic strings of the heterotic string theory which has a repulsive rather than attractive “gravity” effect this pure dark energy can explain accelerated cosmic expansion in a quite satisfactory way [18] [25] [30] . Equally interesting, if not even more so, is the almost identical role which Gross’ 16 extra dimensions and the signature ![]()
of our K3 Kähler manifold plays with respect to pure dark energy. It was R. Thom who showed that the signature is a cobordism invariant and thus we can think of it as the outer part of the quantum wave and consequently as a negative anti-gravity-like force. The reader of this paper must have surely discovered the profound role that higher spacetime dimensionality plays for the present work. It all started with T. Kaluza’s five dimensions [41] [52] which we used here extensively as in the ![]()
of ordinary energy density and ![]()
of the dark energy density. Besides being an outstanding mathematics professor, T. Kaluza senior was a great many other things including having good knowledge of many languages besides his German mother tongue. Remarkably it is said that Arabic was his favourite foreign language or at least that is what his son who was the author’s maths teacher told him in Germany on a memorable occasion recounted in the following reference [52] . It is relatively easy from this discussion to show that Zitterbewegung is the result of a fractal random Cantor set quantum path with a Hausdorff dimension equal to a classical path D = 1 plus a fractal noise![]()
, i.e. ![]()
leading us to a quantum physics without quantum mechanics [61] . This conclusion leads us to the deep realization that fractal spacetime is the reason for dark energy and Arend Olbers’s dark sky paradox [62] .
10. Epilogue
Having basically obtained the present results in dozens of different methods and theories, it is surely sensible to ask what the thread is relating all of them or what the trouble is with basic physics that such a simple problem becomes a huge mystery as is the case for quantum entanglement and dark energy. The present author is convinced that the muddle is basically connected not with physics but with scientific philosophy and pure mathematics, especially transfinite set theory which makes a definite distinction between zero, empty and insubstantial nothingness as was done for instance in the work of A. Connes in his noncommutative geometry [56] and as used extensively in nonlinear dynamics, chaos and fractals [30] - [38] . It is quite conceivable that orthodox quantum mechanics is a historical but important accident and that it could have been possible to have modern physics realized via zero and empty sets plus extra dimensions instead of orthodox quantum mechanics. We mean we could have quantum physics without quantum mechanics [59] . Now we are in a reasonably good position to answer our initial question in the Epilogue (Section 2). The question was why Dirac’s bra and ket and not any other formulations lead to Hardy’s first exact golden mean quantum entanglement solution ![]()
where ![]()
is the golden mean. Our answer is educated guess work which deep thinkers like Gell-Mann, Hartle, Stapp, Wheeler, ‘tHooft and much earlier, K. Menger [24] [46] [48] were seriously considering. It is the fundamental and philosophical logical necessity to abandon the concept of a point for something more fundamental. An object with a small extension as a superstring is definitely better than a point but it is not yet sufficient. We need transfinite set theory, which is the mathematical origin of what is nowadays called fractals. Once we admit Cantorian geometry we find undreamed of simplicity and new dualities combining fields with spacetime to something new in physics. The nearest thing to that in the not too distant past is ‘tHooft’s renormalization [25] fractal spacetime and we could claim with some confidence that the present work goes a long way in this direction. Once these basic facts are accepted then most of the weirdness of quantum physics evaporates and we recognize quantum entanglement as a natural consequence of empty sets and zero measure geometry and that state vector reduction is nothing more than an empty set becoming a non-empty zero set due to intrusive measurement. In fact, seen that way, the density matrix may be replaced by the density of spacetime as shown in the present paper. However, at the end of the day, without moving from our traditional number systems to the golden mean based number system of E-infinity, we may understand a great deal but we could not possibly be able to calculate as many accurate results as we have here. In other words, the golden mean number system used here is part and parcel of the general theory and not coincidental to it. The final grand design is a quantum physics without quantum mechanics [59] [61] which is replaced by incorporating the zero set and the empty set of transfinite set theory on a fundamental level in the very roots of physics where physics, logic and pure mathematics are one and the same thing [24] - [44] .