Black Holes or Dark Stars—What Follows from the General Relativity Theory ()
1. Introduction
The existence of Dark Stars was predicted by J. Michel in 1783 and P. Laplace in 1796 [1] [2] . As known, the escape velocity for a spherical body with radius R and mass m is
 (1)
(1)
in which c is the velocity of light and
 (2)
(2)
is the so-called gravitational radius which depends on the gravitational constant G and the sphere mass. For the sphere with constant density µ in the Euclidean space
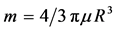 (3)
(3)
Substituting Equations (2) and (3) in Equation (1), we get
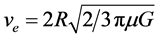 (4)
(4)
According to the reconstructed Laplace calculation, for Earth with density mE = 5520 kg/m3 and radius RE = 6371032 m, Equation (4) yields ve = 11,000 m/s which is 27,270 times less than the velocity of light. Because ve in Equation (4) is proportional to R increasing R up to 1.62 × 1011 m which is 249.6 times higher than the radius of Sun (6.96 × 108 m) we arrive at ve = c. This calculation allowed Laplace to conclude that the star with the density of Earth and the radius which is about 250 times larger than the radius of Sun is not visible and can be referred to as the Dark Star. Later, the idea of Dark Stars based on CGT and the corpuscular model of light was abandoned by Laplace and the subsequent authors [1] [2] . The present paper contains an attempt to revive this idea within the framework of GRT. Under some assumptions, we obtain the solution of GRT equations which corresponds to the object that can be treated as the Dark Star.
2. General Relativity Equations
The general form of the line element in spherical coordinates r, q, j can be presented as
 (5)
(5)
For spherically symmetric static problems, the components of the metric tensor gij depend only on the radial coordinate r. Material properties of space are determined by three components of the energy tensor ,
,  ,
,  which satisfy the conservation equation [3]
which satisfy the conservation equation [3]
 (6)
(6)
where (…)¢ = d(…)/dr.
In accordance with the basic mathematical idea of GRT, Equation (6) is satisfied identically if the tensor  is expressed in terms of the metric coefficients by the following Einstein equations:
is expressed in terms of the metric coefficients by the following Einstein equations:
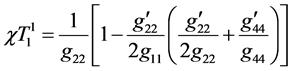 (7)
(7)
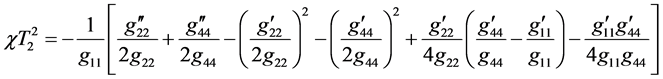 (8)
(8)
 (9)
(9)
Here,
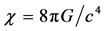 (10)
(10)
is the GRT gravitational constant. Because the left-side parts of these equations are linked by Equation (6), only two of three Equations (7)-(9) are mutually independent. Traditionally [3] , the simplest combination of these equations, including Equations (7) and (9) is used to determine the metric coefficients g11 and g44 whereas Equation (8) is satisfied identically for any function g22(r) Possible forms of the solution of two equations (7) and (9) with three unknown functions are discussed by Vasiliev and Fedorov [4] .
Because the metric coefficients must be positive, introduce new functions, i.e., take g11 = g2(r), g22 = r2(r), g44 = h2(r). Consider the external and the internal spaces for the sphere with radius R.
For the external empty space (r ³ R) we have . Then, Equation (6) is satisfied automatically, whereas Equations (7) and (9) reduce to
. Then, Equation (6) is satisfied automatically, whereas Equations (7) and (9) reduce to
 (11)
(11)
Index “e” corresponds to the external space. Thus, we have two equations for three functions ge(r), re(r), he(r) and to solve the problem, we need one more equation.
For the internal space of the solid sphere (0 £ r £ R),
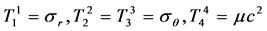
where sr and sq are the radial and the circumferential stresses acting in a solid sphere. Then, Equations (7) and (9) become
 (12)
(12)
![]() (13)
(13)
Index “i” corresponds to the internal space. The conservation equation, Equation (6), takes the form
![]() (14)
(14)
This is actually the equilibrium equation for a solid sphere [5] . As known, to determine the stresses, the equilibrium equation should be supplemented with constitutive equations which link stresses and strains in a deformable solid and with the compatibility equations for the strains. Such equations do not exist in GRT, and this theory cannot be applied to study gravitation in deformable solids [6] . The only particular case for which the solution can be found corresponds to the sphere consisting of perfect fluid. In this case, sr = sq = ?p(r) where p is the pressure in the fluid. Then, Equation (14) reduces to
![]() (15)
(15)
Thus, for the case of a fluid sphere we have three equations, Equations (12), (13) and (15), which include four unknown functions gi(r), ri(r), hi(r) and p(r). Again, to solve the problem we need one more equation.
The solution for the external space must satisfy the asymptotic condition according to which it must degenerate into CGT solution with a distance from the sphere, the solution for the internal space must satisfy the regularity condition at the sphere center, and both solutions must meet the boundary conditions on the sphere surface.
3. Schwarzchild’s Solution and Black Holes
Both external and internal problems for a fluid sphere were solved by K. Schwarzchiuld in 1916. The equation that forms the complete set with the equations presented above was taken in the form p(r) = r.
3.1. External Space
Putting pe = r in Equations (11), we arrive at
![]()
The solutions of these equations are
![]() (16)
(16)
The integration constants C1 and C2 can be found from the asymptotic conditions according to which for r ® ¥ the obtained solution must reduce to the CGT solution that is expressed in terms of the Newton gravitation potential j [7] , i.e., to
![]() (17)
(17)
As a result, Equations (16) take the well known form [3]
![]() (18)
(18)
As follows from the derivation of Equations (18), they include the radius rg which is specified by Equation (2) and corresponds to the classical gravitation theory. Equations (18) show that the Schwarzchild solution determines the metric coefficients of the external space in terms of the sphere gravitational radius which depends on the sphere mass only and does not take into account the internal structure of the sphere, i.e., the structure of the source of gravitation. Such situation is typical for CGR, i.e., for the solution in Equations (17), which is unique. However, for GRT the situation can be different, because the function g22 = r2(r) in Equation (5) can be chosen in different forms. Consider, for example, De-Donder-Fock solution which satisfies the so-called harmonic coordinate condition. Omitting mathematical formulation and physical interpretation of this condition which can be found elsewhere [8] [9] , presume that the function r(r) has the following form: r(r) = r + rg/2. Then, the solutions of Equations (11) become [8] [9]
![]() (19)
(19)
For r ® ¥, these solutions asymptotically reduce to Equations (17). Thus, Equations (19) satisfy all GRT equations and asymptotic conditions, but do not coincide with the Schwarzchild solution in Equations (18).
3.2. Internal space
For the internal space of the fluid sphere and r(r) = r, Equations (12) and (13) reduce to
![]() (20)
(20)
![]() (21)
(21)
In conjunction with Equation (15) for the pressure we have three equations for three unknown functions gi(r), hi(r) and p(r) For the sphere with constant density m, the solution of Equation (21) which satisfies the regularity condition at the sphere center r = 0 is [3]
![]() (22)
(22)
This solution must satisfy the boundary condition on the sphere surface according to which gi(R) = ge(R). Using Equations (18), we have
![]() (23)
(23)
and finally get [3]
![]() (24)
(24)
Consider Equation (20) for hi. Substituting Equation (24), we arrive at
![]() (25)
(25)
Substituting Equation (25) in Equation (15) and using Equation (10) for c, we get the following equation for the pressure in the fluid:
![]() (26)
(26)
The general solution of this equation is [3]
![]() (27)
(27)
The integration constant C3 can be found from the boundary condition on the sphere surface according to which p(R) = 0. The resulting expression for the pressure is [3]
![]() (28)
(28)
Thus, the Schwarzchild solution is specified by Equations (18) for the external space and Equations (24), (25), (28) for the internal space of the fluid sphere with constant density.
3.3. Analysis
To demonstrate the specific features of the Schwarzchild solution, consider it for the sphere surface r = R. For this surface, we have
![]()
As can be seen, for the sphere with radius R = rg, gR becomes singular and hR is zero. This result has not been accepted by A. Einstein [10] who expected that GRT could not be valid for the sphere with radius close to rg. Later, the singularity of the Schwarzchild solution gave rise to the idea of Black Holes and rg was referred to as the radius of the horizon of events of the Black Hole [1] [2] . However, recent results in Mechanics of Solids [11] allow us to conclude that singular solutions do not have physical nature and are the formal consequences of the discrepancy between physical and mathematical models. Particularly, the mathematical model of space specified by Equation (5) is simplified by the condition r(r) = r which is not properly justified. As a result, the Schwarzchild solution suffers from several shortcomings discussed below.
First, the critical radius rg in GRT solution in Equations (18) and (24) is the same that in Equation (2) which follows from CGT.
Second, the solution for gi in Equation (24) satisfies the boundary condition on the sphere surface only if Equation (23) is valid. Substituting rg from Equation (2) and c from Equation (10) in Equation (23), we can derive the equation for the sphere mass which becomes m = 4/3pmR3 and coincides with Equation (3) corresponding to the Euclidean space. However, the space inside the sphere, in accordance with the basic idea of GRT, is Riemannian. The mass of the sphere with constant density corresponding to the metric form for the line element in Equation (5) is
![]() (29)
(29)
Substituting gi from Equation (24) and taking ri = r, we get
![]() (30)
(30)
The second part of this equation is the power decomposition with respect to rg/R. As follows from Equations (3) and (30), the sphere mass corresponds to the Euclidean space only if rg = 0. In the general case, rg ³ 0 and the sphere mass, corresponding to the Schwarzchild solution must be specified by Equation (30). However, in this case ge(R) ¹ gi(R) and the boundary condition for the external and internal spaces cannot be satisfied on the sphere surface.
Third, Equation (28) for the pressure demonstrates rather specific behavior of the function p(r, R) [12] . Consider the pressure at the sphere center. Taking r = 0 in Equation (28), we get
![]() (31)
(31)
The denominator of this expression becomes zero if R = Rs = 9/8rg = 1.125rg [13] . Thus, the pressure becomes infinitely high at the sphere center if R = Rs. This result is traditionally used to justify the existence of Black Holes [1] . However, Rs does not coincide with rg. Then, Equation (31) specifies the pressure if R < Rs but this pressure is negative (or the density is negative) which does not have physical meaning. Finally, if we use the general solution in Equation (27) and take r = rg, we get
![]()
On the sphere surface r = R, we have p(R) = ?mc2/3 and the boundary condition p(R) = 0 cannot be satisfied.
3.4. Generalized Schwarzchild Solution for the Internal Space
The original Schwarzchild solution for the internal space discussed in Section 3.2 has been obtained for the sphere with constant density m. Within the framework of the Schwarzchild assumption, i.e. r(r) = r, consider the sphere for which m(r) is an arbitrary function of the radial coordinate. In this case, the solution of Equation (21) that generalizes the solution in Equation (22) for the constant density is
![]() (32)
(32)
For the sphere surface, we get
![]()
where
![]()
is the sphere mass corresponding to the Euclidean space. If we use Equations (18), (2) and (10) for ge, rg and c, we can conclude that Equation (32) satisfies the boundary condition gi(R) = ge(R). However actually, the sphere mass with the metric coefficient specified by Equation (32) does not correspond to the Euclidean space.
Thus, in the general case of the sphere whose density is an arbitrary function of the radial coordinate and r(r) = r, the boundary condition for g(r) can be satisfied only if the geometry of the internal space is Euclidean which is not the case. The reason of this situation follows from Equation (13) which has, in general, the second order. Under the condition r(r) = r, it reduces to the equation of the first order and the corresponding solution does not contain the proper number of integration constants that are required to satisfy the boundary conditions.
4. Dark Stars
4.1. General Solution
Consider the general metric form of the line element specified by Equation (5) in which ![]() is some unknown function. For the external space, the second equation in Equations (11) can be reduced to
is some unknown function. For the external space, the second equation in Equations (11) can be reduced to
![]()
and has the following general solution:
![]() (33)
(33)
Substituting this result in the first equation in Equations (11) and integrating, we get
![]() (34)
(34)
Assume (and further prove) that the following asymptotic conditions are valid for re® ¥:
![]() (35)
(35)
i.e., that at a distance from the sphere re degenerates into r. Then, Equations (33) and (34) asymptotically reduce to Equations (17) corresponding to CGT if C4 = -rg and C5 = 1. Finally,
![]() (36)
(36)
For the internal space, Equation (13) can be transformed to
![]() (37)
(37)
Assume (and further prove) that at the sphere center
![]() (38)
(38)
For the sphere with constant density m, the solution of Equation (37) that satisfies the regularity condition at the sphere center is
![]() (39)
(39)
For r(r) = r Equations (36) and (39) coincide with the Schwarzchild solutions in Equations (18) and (22). However, in contrast to Equations (18) and (22), the obtained equations include the derivative r¢(r).
4.2. Internal Space
Now, we need to specify the function r(r). Recall that the main shortcoming of the Schwarzchild solution is the discrepancy between the Euclidean form of the sphere mass which allows us to satisfy the boundary condition ge(R) = gi(R) and the actual mass (30) which corresponds to the Riemannian internal space of the sphere.
Note that the mass in Equation (30) depends on gravitation. Being discussed by, e.g. Zeldovich and Novikov [14] , the dependence of mass on gravitation, does not seem to correspond to the principle of equivalence of gravitational and inertial masses. Indeed, the inertial mass shows itself under the action of forces whose nature is different from the nature of gravitation. Anyway, as known [3] , any assumption may exist in GRT if the resulting solution is feasible. Thus, suppose that gravitation does not affect the sphere mass which remains the same that in the absence of gravitation and corresponds to the Euclidean space. As follows from Equation (29), the sphere mass corresponds to the Euclidean space if
![]() (40)
(40)
which is the equation for the function ri(r). Now, since the mass is Euclidean, Equation (23) of the Schwarzchild solution is valid and we can transform Equation (39) to the following final form:
![]() (41)
(41)
Substituting Equation (41) in Equation (40), we arrive at the following differential equation for the function ri(r):
![]()
The solution of this equation which satisfies the condition in Equation (38) is
![]() (42)
(42)
where
![]()
Equation (42) implicitly specifies the function ri(r) which changes from ri = 0 that corresponds to the sphere center to ri(R) = rR that corresponds to the sphere surface. Taking r = R in Equation (42), we arrive at the following implicit equation for rR:
![]() (43)
(43)
4.3. External Space
The metric coefficients for the external space must satisfy the asymptotic conditions in Equations (35) and the following boundary conditions on the sphere surface r = R:
![]() (44)
(44)
To satisfy these conditions, assume that Equation (40) is valid not only for the internal space, but for the external space as well, i.e.,
![]() (45)
(45)
Matching Equations (40) and (45), we can conclude that if the second boundary condition in Equations (44) is satisfied, the first of these conditions is satisfied automatically because r is continuous. Substituting the first equation in Equations (36) in Equation (45), we get the following differential equation for the function re(r):
![]() (46)
(46)
The solution of equation (46) which satisfies the second boundary condition in Equations (44) is
![]() (47)
(47)
where
![]()
This solution is valid for rR £ re < ¥ where rR corresponds to the sphere surface. For the external space, we need to check the asymptotic conditions in Equations (35). Dividing Equation (47) by ![]() and taking re ® ¥, we can readily prove that re ® r. Differentiating Equation (47) with respect to re and dividing the result by
and taking re ® ¥, we can readily prove that re ® r. Differentiating Equation (47) with respect to re and dividing the result by![]() , we can prove that the second condition in Equations (35) is also valid. Thus, for re ® ¥, Equations (36) reduce to the Schwarzchild solutions in Equations (18) which, in turn, degenerate into the CGT solutions in Equations (17).
, we can prove that the second condition in Equations (35) is also valid. Thus, for re ® ¥, Equations (36) reduce to the Schwarzchild solutions in Equations (18) which, in turn, degenerate into the CGT solutions in Equations (17).
4.4. Critical Radius
Consider Equation (47) from which it follows that the real solution exists if re ³ rR ³ rg. Thus, the minimum possible value of the function rR that corresponds to the sphere surface is rg specified by Equation (2). Taking rR = rg in Equation (43), we arrive at the following equation for the minimum possible value of the sphere radius Rg:
![]() (48)
(48)
The solution of equation (48) is Rg = 1.115rg. For the sphere with R < Rg, rR < rg and the solution in Equation (48) becomes imaginary.
4.5. Comparison with the Schwarzchild Solution
As follows from the foregoing derivation, the obtained solution gives the critical radius similar to the horizon of events radius of the Black Hole in the Schwarzchild solution. However first, this radius does not coincide with rg which actually follows from CGT. Second, for the sphere with the critical radius Rg, the solution is not singular. Indeed, Equations (40), (45) and (47) for r = Rg yield ge(R) = gi(R) = 1.243 and re(R) = ri(R) = 0.8968R. Third, for sphere with radius R < Rg, the solution becomes imaginary which means (in accordance with A. Einstein prediction) that GRT equations are not valid in this case. The dependences r(r) and g(r) corresponding to the limiting case R = Rg = 1.115rg are shown in Figure 1 with solid lines. Dashed lines correspond to the limiting case (R = rg) of the Schwarzchild solution.
As can be seen, the obtained solution coincides with the Schwarzchild solution at r = 0 and r ® ¥. The most pronounced difference is observed in the vicinity of the sphere surface. For R = rg, the Schwarzchild solution is singular at r = R, whereas the obtained solution is finite.
To proceed, find the pressure p in the fluid. Taking sr = -p in Equation (12) and substituting gi from Equation (41), we arrive at the following equation for hi:
![]() (49)
(49)
in which, as earlier, (…)¢ = d(…)/dr.
Changing r to a new variable ri, we can transform Equation (49) to
![]() (50)
(50)
Integration of Equation (50) allows us to satisfy the boundary condition he(R) = hi(R). The pressure p entering Equation (50) is specified by Equation (15).
![]()
Figure 1. Dependences of the space metric coefficients on the radial coordinate.
Changing r to ri in this equation, we get
![]() (51)
(51)
Substituting Equation (50) in Equation (51), we obtain the following equation for the pressure:
![]() (52)
(52)
As can be seen, Equation (52) is analogous to Equation (26) and its solution which satisfies the boundary condition p(rR) = 0 is similar to Equation (28), i.e.,
![]() (53)
(53)
The pressure at the sphere center (ri = 0) is
![]() (54)
(54)
The denominator of Equation (54) becomes zero if R = 1.013rg which is less than the critical radius Rg = 1.115rg. Thus, in contrast to the Schwarzcnild solution in Equation (31), the pressure is not singular. For the sphere with the critical radius R = Rg, we get p0 = 0.808mc2. The dependences of the normalized pressure on the radial coordinate are presented in Figure 2. Solid line demonstrates the obtained solution, Equation (53), for the sphere with the critical radius R = Rg. Dashed line corresponds to the Schwarzchild solution, Equation (28), for the sphere with the limiting radius R = Rs = 9/8rg.
Thus, the critical radius is Rg = 1.115rg. Using Equation (2) for rg we get
![]() (55)
(55)
As shown by Vasiliev and Fedorov [15] , for the sphere with radius Rg (as for the Black Hole) the escape velocity is equal to velocity of light and, following P. Laplace, this sphere can be referred to as the Dark Star. Naturally, the parameters of this object are different from those found by Laplace.
Thus, we can conclude that GRT equations are valid for the problem under study if R ³ Rg. The sphere with R < Rg is statically stable. Assume that due to high gravitation the Dark Star with radius R ≤ Rg attracts some additional fluid mass with the same density and the star mass becomes higher. Then, in accordance with Equation (55) the critical radius increases in proportion to the mass. However, the sphere radius R is proportional to m1/3. So, the inequality R < Rg remains valid and the Dark Star remains invisible.
The obtained result is of a qualitative nature because it corresponds to the fluid sphere with constant density, i.e., to the object which is not quite realistic.
![]()
Figure 2. Dependences of the normalized pressure in the fluid on the radial coordinate.
5. Conclusion
As follows from the foregoing discussion, the singular Schwarzchild solution of the spherically symmetric GRT problem satisfies the boundary condition for the space component of the metric tensor on the sphere surface only if the sphere mass is Euclidean which is not the case in GRT.
The proposed solution of the problem based on the assumption according to which the gravitation does not affect the sphere mass, in contrast to the Schwarzchild solution, is not singular and specifies the critical radius of the sphere limiting the application of GRT equations to the spheres whose radii are equal or larger than the critical value. The obtained solution is valid for the sphere consisting of a perfect incompressible fluid. Thus, the objects that are similar to Dark Stars in the Classical Gravitation Theory can follow from the General Relativity Theory.
Acknowledgements
The author thanks L.V. Fedorov for collaboration.