1. Introduction
Edwin Hubble’s experimental confirmation of the expansion of the universe which was theoretically predicted by Friedmann, represents a landmark in the history of cosmology. The prediction came in 1922 [1] and the confirmation for the same came later in 1929 [2] . From his experimental observations Hubble concluded that v = Hr, where v is the velocity of the moving galaxy, r is its distance from the earth and H is a constant which we call Hubble’s constant. However, the experimental values of H found by several research groups [3] [4] [5] after Hubble have confirmed that the so called constant H is no longer constant for all values of the distance r, but it goes on gradually decreasing as r increases. Hence the problem of finding a suitable theoretical relation between v and r is there in the field right up to now. This paper addresses this problem.
Here in this paper we derive afresh the relation between the velocity v of a unit mass at the edge of the universe and the radius r of the universe. For this, we use one of our cosmological Equations derived in [6] . It is of the form
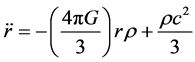(1)
where ρ is the Matter-Energy density of the universe. The above cosmological equation was derived by us from a set of axioms proposed by us for Space [6] . In this reference paper [6] , along with the universal constant c (velocity of light) and G (gravitational constant), the density ρ of the universe is considered to be a universal constant characteristic of our universe. As the universe expands the constancy of the ρ is maintained by the continuous popping up of energy― momentum tensor from the Space due to quantum fluctuations. Cosmological Models with constant ρ are already there in recent cosmological studies [7] . In this connection, the following remark by Lawrence [5] will be of some interest here: “While inflation demonstrates how empty space endowed with energy can effectively create everything we see, along with an unbelievably large and flat Universe, it would be disingenuous to suggest that empty space endowed with energy which drives inflation, is really nothing”.
The term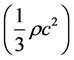 
in Equation (1) represents the factor that drives the ex-
pansion of the universe. However, to explain the expansion of the universe, the standard Big-Bang Model assumes the presence of an energy density giving rise to the necessary repulsive force to drive the boundary of the universe away. Since the origin and the cause of such energy are not known it is called dark energy. Regarding the expansion of the universe, the following needs a mention.
Einstein had a premonition that the boundary of our universe is stable. To satisfy his premonition Einstein added a kind of a repulsive force to balance the gravity. This adhoc repulsive force is represented in his equation by the factor ⋀, called cosmological constant. The energy corresponding to the cosmological constant is nowadays called dark energy. Also, Lemaitre [8] showed that the expansion of the universe would eventually become accelerated when ⋀ is greater than zero. In our work the continuous popping up of particles from the so called
empty Space which keeps the term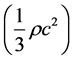 
always constant, is the source for
the repulsive force pushing the boundary of the universe away with an acceleration.
2. Hubble’s Law Extended
Solving Equation (1), we get
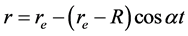(2)
where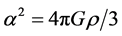 
and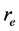 
is the distance at which 
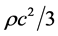becomes equal to 
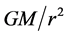and its value is 1.11 × 1026 m (117.3 billion light year). R is the minimum value of r at t = 0, 2π/α, or n2π/α where n is an integer. Differentiating Equation (2) with respect to time we have,
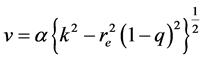
where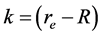 
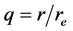
Since compared to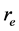
, R is infinitely small,
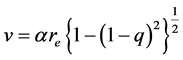(3)
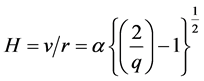(3a)
Equation (3a) agrees with recent experimental observations [9] [10] which conform that the value of H is decreasing as r increases. For large values of r when it tends to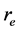
, replacing 
with r, in Equation (3) we get v = αr. Equa-
tion (3) thus reduces to the simple Hubble’s Law v = Hr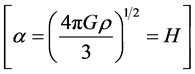 
when r tends to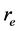 
in which case ![]()
tends to zero. Hence, Equation (3) can be considered as an extended version of Hubble’s Law. From Equation (3) we thus regain Hubble’s Law for large values of r and we have an advantage too. The advantage is the significant insight that we get regarding the Hubble con-
stant which in the above derivation turns out to be ![]()
In our
universe, c, G, ρ, H and ![]()
seem to be inter related. Equation (3a) is represented by the following graph Figure 1.
It might be of some interest to give here the work of Moraes et al. [10] regarding the variation of H with time. In [10] , the authors present their ![]()
concept of gravity along with Einstein’s field tensor ![]()
and Robertson- Walker metric and derive the following formula for the Hubble factor H.
![]()
(4)
where ![]()
![]()
Figure 2. Time evolution of the Hubble parameter. The (blue) dotted line stands for β = π, while the (green) dot-dashed and (red) solid lines for β = 5π and β = 30π, respectively.
For three values of β, they have obtained three different graphs as shown above in Figure 2.
The nature of variation of H discussed in this paper and given in Figure 1 is strikingly similar to the nature of variation of H given in Figure 2. It is gratifying to note that while Moraes et al. obtained Equation (4) by combining Einstein field tensor and Robertson?Walker metric, we obtain our Equation (3a) just from our axioms using simple differential equation.
3. Conclusions
It is well known that the formula PV = RT deduced from the experiments was given an extended version by Van der Waal and the extended version is![]()
. This extended version was derived by him by using the postulates of kinetic theory. Our work presented here is very similar to this in the sense that we also proposed a fresh set of axioms and from the axioms the extended Hubble’s Law in Equation (3) was derived.
Proposing a new set of axioms and deriving fresh relations from them represent a significant step in our understanding of the universe. As is well known, Einstein framed his axiom for light and from that axiom he obtained equations governing the parameters of a particle in motion. Going subtler, we have framed axioms for Space and from them we obtained our cosmological equations [6] and further results there from. That our axioms about Space are able to lead us to a relation between the radius of the universe and its expansion velocity and that the relation thus obtained fairly agrees with the experimental observations show that our axioms are fairly good and the philosophical revelations of Shri. Vethathiri Maharishi (A great thinker of Tamil Nadu, India) which gave us the necessary clue and the guidelines to frame our axioms are really strong enough.
The possibility of deriving further results regarding the evolution of the universe by using our cosmological equations is under investigation and the results will be published elsewhere.
Acknowledgements
The authors remain extremely thankful to the referees for their comments which largely improved the contents and the presentation of this paper.
The authors place their deepest reverence to Shiri. Vethathiri Maharishi for having taught us his philosophy of Space in all details and in all depth. They remain highly grateful to Mrs. and Mr. Raj Taneja of Chicago, Mrs and Mr. Vijay Arora, New Jersey, Mrs. and Mr. Dr. Panneer Selvam of Florida International University, Miami, Mrs. A. Thayar, Pollachi, Mrs, and Mr. Vikram Kannan, New Jersey and Mrs. and Mr. Babu Prasath of Pollachi and Mrs. M. Vimala, Miss. M. Devatharshini, and Mr. M. Srivatssan, Mr. M. Asswin, Kumbakonam for their constant interest in this work.