1. Introduction
In this paper, we continue the efforts of the Computational Theory of Intelligence (CTI) first introduced in [1] . Here, we investigate the influence of feedback in intelligence processes. It is our intent to show that feedback provides a momentum component to the learning process.
The fact that feedback is effective in various situations especially those involved with time series data is not novel. Some notable studies include [2] [3] [4] among others. Our intent is to provide a generalized theoretical approach to the addition of feedback into the intelligence process as understood through the framework of CTI.
We begin with necessary terminology and notation. Recall from [1] that given the two sets 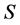 and
and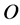 , the intelligence mapping
, the intelligence mapping , at a particular time,
, at a particular time,  is represented by
is represented by
 (1)
(1)
where 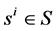 and
and 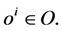 This mapping may be updated via the gradient of a learning function
This mapping may be updated via the gradient of a learning function 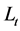
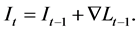 (2)
(2)
For the remainder of this paper, we will investigate the effects of introducing feedback into the formulation discussed above.
2. Feedback
For the purposes of this paper and its application to the Computational Theory of Intelligence, we define feedback as a process by which the result of a previous iteration of the intelligence process is combined with the input into a subsequent application. Typically, the epochs differ by one iteration, and we will proceed with this in mind.
Let us consider Equation (1) and make a slight adjustment by considering the above assumptions, and the output of the previous epoch 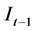
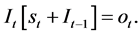 (3)
(3)
Note that, due to the application of the addition operation between respective elements of  and
and 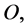 we are obliged to ensure that this operation is meaningfully defined between elements of these two sets. Also, for notational brevity we have removed the superscripts
we are obliged to ensure that this operation is meaningfully defined between elements of these two sets. Also, for notational brevity we have removed the superscripts 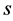 and
and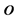 . We will proceed in this manner when the context is clear.
. We will proceed in this manner when the context is clear.
Explicit enumeration of each step in the recursive process gives us the following:
 (4)
(4)
At this point we cannot move forward until we pontificate as to the nature of the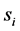 . At the beginning of this section, our intent was to simply incorporate knowledge from previous iterations into the intelligence process. It therefore stands to reason that each subsequent input is related to the next in some way, as if perhaps by some function
. At the beginning of this section, our intent was to simply incorporate knowledge from previous iterations into the intelligence process. It therefore stands to reason that each subsequent input is related to the next in some way, as if perhaps by some function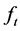 . In particular, if
. In particular, if ![]() depends on some initial value
depends on some initial value![]() , we have
, we have
![]() (5)
(5)
This insight will prove extremely valuable in determining in what types of applications feedback will be most efficacious.
Implementing Equation (5), Equation (4) becomes
![]() (6)
(6)
2.1. Momentum
If we carry the ideas of this section further, we can apply our discussion about feedback to derive momentum terms to the learning function. If we expand the definition of the learning function taking into account the developments from Equation (6), we have
![]() (7)
(7)
Applying the gradient operator as per Equation (2), we have
![]() (8)
(8)
We may expand the above expression through diligent application of the chain rule:
![]() (9)
(9)
Distributing terms and rearranging,
![]() (10)
(10)
The above may be thought of as a summation of momentum terms, from the most recent iteration all the way back to the initial epoch.
Equation (10) may be written more compactly as
![]() (11)
(11)
The momentum terms in Equations (10) and (11) are worth mention. As time increases, the amount of products in each momentum term increases. This insures automatically that more recent momentum terms will dominate over those more distal in time (since we are assuming each term is less than or equal to unity). Weighting more recent iterations is a natural consequence of our formulation.
2.2. Computational Self-Awareness
Finally, it might be insightful to quantify the ratio of the two sources, new information and that which came from feedback, at some particular epoch![]() . If we denote this quantity
. If we denote this quantity![]() , then
, then
![]() (12)
(12)
For reasons we will discuss later, we will refer to the quantity ![]() as the computational self-awareness of the agent facilitating the intelligence process at epoch
as the computational self-awareness of the agent facilitating the intelligence process at epoch![]() . Note that as the input signal tends to zero, so tends the computational self-awareness to infinity.
. Note that as the input signal tends to zero, so tends the computational self-awareness to infinity.
3. Stability
One of the core tenets of CTI [1] is that ![]() must minimize information entropy locally. We must show that this is still the case even in the presence of feedback. It is well established [5] that recursive feedback in algorithms leads to instability, chaos, and other nonlinear effects. We will apply the study of such systems to this application using Lyapunov stability theory. In particular, we highlight the fact that the entropy of a system increases with the value of the Lyapunov exponent
must minimize information entropy locally. We must show that this is still the case even in the presence of feedback. It is well established [5] that recursive feedback in algorithms leads to instability, chaos, and other nonlinear effects. We will apply the study of such systems to this application using Lyapunov stability theory. In particular, we highlight the fact that the entropy of a system increases with the value of the Lyapunov exponent ![]() [6] . By [7] , the Lyapunov exponent may be expressed as
[6] . By [7] , the Lyapunov exponent may be expressed as
![]() (13)
(13)
In a similar manner to our derivation in Section (2.1), we can show that this works out to be
![]() (14)
(14)
by our definition of![]() . Since
. Since ![]() is a function parameterized by
is a function parameterized by![]() , we cannot proceed further in the general case. Thus, the condition for entropy minimization at
, we cannot proceed further in the general case. Thus, the condition for entropy minimization at ![]() to hold is that
to hold is that![]() .
.
4. Conclusions
In this paper, we provided a generalized theoretical framework concerning the effect of feedback in the intelligence process. From our derivation, we were able to conclude that feedback adds a “momentum” component to the learning pro- cess, which is of particular interest for time series type data.
We also discussed computational self-awareness, purely in the context of the ratio of feedback to input. The concept of self-awareness is highly contentious and philosophical and we wish to keep this paper technical. For our purposes, this is simply the extent to which the agent applies feedback in the intelligence process relative to input data.