Possibility of Excitation of Magnetospheric Modes by Strong Geomagnetic Storms ()
1. Introduction
Geomagnetic storms (GS) are variations of short period on the Earth’s magnetosphere, ranging a few hours to some days. A super geomagnetic storm (SGS) is a GS characterized by values of the Dst index below −250 nT, and this kind of phenomena seems to show some oscillations during its declining phase on the times series of Dst index. Fortunately, they are not (as the more intense earthquakes) very frequent.
The GS classification is done according with the intensity of the lowest value measured during the event, and as seen in the work from [1] , they can be labeled as seen on Table 1. All GS events have three common phases that can be observed on the time series of the Dst index. According to the studies of [2] and [3] , these phases have the following features:
- A Storm Sudden Commencement (SSC) marks the beginning of an increasing of DST index above the mean values. This increasing occurs because of the solar wind’s increased pressure, due to the impact of an ICME (an Interplanetary CME, originated from the impact of the fast solar wind from a CME that comes
![]()
Table 1. Types of GS according to DST index following [1] .
from upper regions of Sun’s Corona with the daily solar wind that has a mean value of 400 km∙s−1) on the dayside magnetosphere. The result is an increase on the ring current in the eastward direction of the Earth. This is the initial phase of the GS, and can take from some minutes to a few hours;
- Then, comes the main phase. A southward magnetic Bz component (that presents negative values on the time series) in the Interplanetary Magnetic Field (IMF) that makes the ring current flows westward, causing a decrease on the geomagnetic field (it is seen on the Dst time series). It can last hours or even some days, and it is where a GS reaches its lowest peak on DST index. It endures as long as Bz stays southward;
- Finally, after reaching the lowest peak on Dst index and the Bz magnetic component of the IMF return to zero or to positive values, the recovering phase of the GS starts, where Dst values slowly recover to the mean values before the SSC. This phase can last from some hours to days.
The origins of GS, according to the works of [4] [5] and [6] , are linked to solar phenomena, namely, the coronal mass ejections (CME) and coronal holes (CH), both phenomena occurring in Sun’s Corona.
Some works, as [7] , presented studies done on calm and geomagnetically active times. In this work, the study is focused on the SGS events. On time series of Dst index, some oscillations during the main and the recovering phases of a SGS can be seen, and these oscillations seem to be a physical mechanism of the Earth’s magnetosphere that tries to recover itself during a SGS. The geoeffectiviness of a GS is linked to the physical mechanism studied by [8] .
This study is a contribution to both, fundamental studies on magnetosphere and to the characterization of the economic and technological impacts that a severe SGS (as the Quebec event on March 1989), can cause. In this study, our aim is to contribute to a better understanding of SGS and its complex dynamics.
2. Data Selection
At the beginning of this study, the selected data for all the GS with index Dst < −250 nT, given on hourly means and available in the period from 1957 to 2014 comes from World Data Center for Geomagnetism, Kyoto (http://wdc.kugi.kyoto-u.ac.jp/). These dataset gave a good idea of the quantity of SGS on this period, as well as the distribution of events.
On Figure 1, some SGS events can be identified between the years of 1957 and 2014. Some gaps can be noted as well, corresponding to periods of solar minima
![]()
Figure 1. Time series for hourly means of DST index from 1957 to 2014. We can see gaps of values < −250 in the middle of the 60 s, a great one between the middle 70 s and the beginning of the 80s, in the middle of the 90 s and after 2006.
on the solar between cycles 20 and 21, between solar cycles 22 and 23, and during solar cycle 24 (the actual cycle, where no SGS occurred until this moment).
But Dst resolution is given on hourly means, which is not enough to study all the oscillations and frequency modes that could exist. For this reason, the Dst time series were changed for Sym-H index time series (given in nT as well), from World Center of Geomagnetism as well, because this one has a resolution given in minute means. According with the explanation of T. Iyemori et al from WDC (that can be found on http://wdc.kugi.kyoto-u.ac.jp/aeasy/asy.pdf), Sym-H index has the same pattern from Dst index, and is derived from 6 magnetic stations between the latitudes between 60˚ and −60˚. So it can be used for analysis of global geomagnetic phenomena [9] .
The dataset for Sym-H starts on 1981, so the study on SGS before this year was not done. Besides, a set of 23 events since then was found on the available data, and they are summarized on Table 2.
With the data starting on 1981, and ending on 2014, there’s one striking feature. As presented on the work of [6] , the 24th solar cycle (the current one, that begun on late 2008) had few intense solar events, or some strong ones that happened, as the CME from 07/23/2012, missed the Earth, as seen on [10] . Consequently, there were not occurrences of SGS since 2006 until 2014, not on Dst time series nore on the Sym-H time series.
Some data on CMEs events from catalogues from the Solar Maximum Mission (https://www2.hao.ucar.edu/mlso/solar-maximum-mission/smm-cme-catalog), and from LASCO/SOHO mission as well (http://cdaw.gsfc.nasa.gov/CME_list/) were checked, due to the need to recognize the physical features of the events.
![]()
Table 2. Magnetic storms which enter our study.
3. Methodology
As seen on Table 2, 23 SGS were detected between 1981 and 2005. Even with some works done previously using the Sym-H index, it was tested to see how much reliable the index can be to this work.
The geomagnetic data used comes from INTERMAGNET global network (http://www.intermagnet.org), and on this part of the study, the data from three magnetic observatories were used: Vassouras (VSS), Huancayo (HUA) and Addis Ababa (AAE). We used the time series of each observatory of H geomagnetic component, the most sensible for GS events, as studied by [6] and [11] and the SYM-H series for the time spam comprising the severe GS that occurred on 11/31/2003 (the so called “Halloween Storm”).
To have a better visualization of the SGS on each dataset, the results for each time series were normalized using the Equation (1):
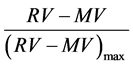 (1)
(1)
where RV are the raw dataset values from each time series (both from magnetic observatories and Sym-H index), MV is the mean value of each time series, and divided each value for the maximum (positive or negative) value found. After the normalization of datasets, all the time series were smoothed.
The values of Sym-H data were multiplied by (−1), just for a better visual adjust. This was done because the H components are given on positive values, by Equation (2):
 (2)
(2)
where X and Y are geomagnetic components of the magnetic field of the Earth on the model proposed by International Association of Geomagnetism and Aeronomy (IAGA), which was adopted in August 2001, and where the geomagnetic components are given on values of X, Y and Z, instead of H, D and Z. Visually, the four time series show the very same pattern for the SGS.
These results can be seen on Figure 2.
The Pearson’s Correlation coefficients between series and their values are shown on Table 3. The Pearson Coefficients, as usual, are calculated in this way:
 (3)
(3)
where 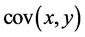 is the covariance between two measurements sets X and Y, and
is the covariance between two measurements sets X and Y, and 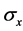 and
and 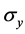 are the standard deviation of each dataset.
are the standard deviation of each dataset.
Clearly, Sym-H index data has a good correlation with H component from three observatories on different regions, what means that Sym-H index can be
![]()
Figure 2. Time series for normalized and smoothed H component and Sym-H index for SGS of October 2003. Time is given on minutes and shows the entire duration of the SGS. Pointed-dashed line is the AAE H component data. Dashed line is for HUA H component, dotted line is for VSS, and solid line for Sym-H series multiplied by a constant factor (−1).
![]()
Table 3. Pearson’s Correlation coefficients (P.C.C.) and significances.
used for the analysis of global geomagnetic events. The great advantage of using Sym-H index on this kind of analysis is that we do not need another observatories geomagnetic data.
This enables the study of negative peaks of Sym-H < −250 nT, to investigate the oscillations during the occurrences of SGS. The use of this index makes things easier, because the values that characterize a SGS are already known from Dst.
The methodology used on this paper is summarized below:
1) Identification of the years that have one or more SYM-H peaks < −250 nT;
2) Identification of the months and days where these SGS were detected;
3) Find the time spams that covers the entire events (beginning, main and recover phases);
4) Find the first value < −50 nT in the beginning of the main phase, and the last value > −50 nT in the recovering phase. This criteria is used due the fact that storms with values above −50 nT are too weak to cause severe damages to Earth’s technological environment;
5) Application of a Fourier Transform (FFT) on the time series, taking the data from the space of time to the space of amplitudes and frequencies;
6) Taking out the negative values of the frequencies from the series, and plot the data;
7) Then, as a last step, an application of log10 on the scale of the amplitudes was done.
4. Results and Discussion
Our method was applied on the SGS of March 13, 1989, and the results can be seen on what follows.
This is the most known SGS of last decades, causing great problems in Quebec, Canada. [12] points clearly: it putted the Hydro-Quebec system down for 9 hours, causing a prejudice of billions of dollars, and almost disrupted the U.S. seaboard power grid as well.
The results after taking out the values above −50 nT from the series at the beginning and the end of the event (because GS with values higher than this thre-
![]()
Figure 3. Times series for Sym-H index during the Quebec’s magnetic storm, March 1989. The lowest value found was −720 nT. Visually, there are many oscillations, as the Earth’s magnetosphere was “trying” to recover itself as show time spams before the lowest value of −720 nT.
shold would not cause severe problems for Earth’s technological environment) are shown on Figure 3.
To put the Sym-H time series in a proper way, the Figure 3 shows the duration of the needed part of the SGS, given in minutes. The analysis began at 03:52 of March 13, 1989, and ended at 23:01 of March 15, 1986, totalizing 4,030 minutes, or two days, 19 hours and 9 minutes.
The lowest value found was −720 nT, being the most severe event in all the studied time series between 1981 and 2014. The main cause of this SGS was a CME “swarm” that happened between March 3 and 10, according with Solar Maximum Mission CME catalogue, as [13] have studied.
We have used the Fourier Transform (FT) on this dataset, to take the data in the domain of time, as a function in the form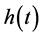 , to another function,
, to another function, 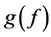 , in the domain of frequency, as seen on Equation 4:
, in the domain of frequency, as seen on Equation 4:
 (4)
(4)
After taking out the negative values from the frequencies and applying a log10 on the Amplitude axis, the result can be seen on Figure 4. The data presents a curious feature: as the amplitude values follow a decreasing tendency, there are some evident modes on frequency with intervals Δf that seem to have an approximately constant value.
We devised a way to find the values for Δf. Firstly, all values of frequencies below 0.1 min−1 were removed from data, due to the existence of great resonance on amplitudes between 0 and 0.1 m−1. Then, a smoothed curve of the data was done, and finally, some peaks were found.
After these procedures, we look for the values of the most outstanding peaks,
![]()
Figure 4. Fourier Transform applied on data for the March 13, 1989 SGS. Visually, some constant frequencies intervals Δf can be seen.
![]()
Figure 5. The smoothed data curve and the peaks found on SGS of March 1989.
as seen on the Figure 5, smoothing the data. So we took the 7 peaks listed on Table 4.
The values found were slightly different from each other, so we looked for the statistical variance (σ).
The mean value found is 0.06 minute−1, that is 60.0 μHz. The founded values for Δf and σ are listed on Table 5.
![]()
Table 4. Frequency modes found on the SGS of March 1989.
![]()
Table 5. Values for Δf and σ, corresponding to Table 4.
So, found that this frequency interval is Δf ≈ 0.06 minutes−1 = 1 mHz, and using the well-known relationship between period and frequency, given by the Equation (5):
![]() (5)
(5)
We find that Δf corresponds to a time interval Δt ≈ 0.3 hours ≈ 18 minutes between each oscillation mode. This value has particularly called our attention because it recovers the same value seen on the work of [14] . This value represents the change of regime of the magnetic component H.
On the set of SGS we have, more 10 present defined modes.
Still having in mind our method of analysis, we present on Figure 6, and Table 6 & Table 7 for the SGS from July 1982; and Figure 7, and Table 8 & Table 9 for the SGS from April 2001.
5. Conclusions
The first feature that can be seen is that, for the case of March 13, 1989 SGS, there are some oscillations present on Sym-H data during the main phase of a SGS. The origin of them could be linked to plasma coupling phenomena occurring due to the intense magnetic reconnection processes, or may be as consequence of consecutive impacts of ICMEs on Earth’s magnetosphere.
In the investigation of Sym-H times series relationship with H geomagnetic component of VSS, HUA and AAE, the data used refers to the Halloween 2003 event, due to the availability of the dataset. The results were as expected, because Sym-H index series is obtained with a corrected average mean value of H component of six stations. However, our analysis proved that Sym-H is trustworthy for this study.
![]()
Figure 6. The smoothed data curve and the peaks found on SGS of July 1982.
![]()
Table 6. Frequency modes found on the SGS of July 1982.
![]()
Table 7. Values for Δf and σ, corresponding to Table 6.
<Δf> ≈ 0.0465 min−1 ≈ 0.775 mHz → <ΔT> = 1290.3226 s ≈ 0.3526 h ≈ 21.156 minutes.
![]()
Figure 7. The smoothed data curve and the peaks found on SGS of April 2001.
![]()
Table 8. Frequency modes found on the SGS of April 2001.
![]()
Table 9. Values for Δf and σ, corresponding to Table 8.
<Δf> ≈ 0.0377 min−1 ≈ 0.6283 mHz → <ΔT> = 1591.5964 s ≈ 0.4421 h ≈ 26.5260 minutes.
As well, on LASCO/SOHO catalogue, there are four CMES events with high speed values are seen between October 19 and October 28. Two of them are HALO CMEs, which according with previous works are the more effective ones to cause a GS. On October 28; the HALO CME had a liner speed of 2459 km/s, and the one for October 29 has a linear speed of 2029 km/s. These are the potential candidates for causing the Halloween 2003 event.
The frequencies scale found by the Fourier Transform are the Nyquist frequencies, so the frequency axis values are fractions of inverse of minutes, from 0 to half of a minute.
One of the values for variances found is great (0.011 minute−1), contrasting with the others, showing that the value for Δf found (0.0319 minute−1) is far from a mean value of the other values found. However, this value for frequency is important to find the coming ones after it. The other variances were very small in contrast with mean Δf values.
The most striking feature of the analysis was that the pattern of Earth’s magnetosphere seems like a dumped harmonic oscillator, whose amplitude decreases as time pass by, but with a constant time interval between each oscillation (in the case, t ≈ 18 minutes). It can be suggesting that all features in the recovering processes in Earth’s magnetosphere after the shock of a severe GS are gradual and constant, as the imputing energy event ceases.
The energy input of a SGS can be linked to physical mechanism previously investigated. The relationship between the velocity of a magnetic cloud and the magnetic field of this structure seems to be the main source of energy of a GS. At the same time, some physical reaction due the plasma coupling on GS can be inputting energy as well and causing these frequencies’ modes.
The values found for the three SGS we analyzed on this paper are 18 minutes (for March 1989 SGS), 21.156 minutes (for July 1982 SGS), and 26.526 minutes (for April 2001 SGS). As said in this work, these values are near the value found in a previous work, where two different power laws intercepted each other. This means that this value between each oscillation is pointing to constant changes in the magnetospheric recovering mechanism for every SGS that has evident frequency modes.
This study had the focus in helping to enhance the knowledge about SGS, the dynamics of the phenomena and its effects on Earth. As well, it provides an easy form of analysis the data, and proofs that Sym-H index can be helpful and used instead of a set of magnetic observatories in some cases.
Acknowledgements
M. A. G. thanks CAPES for the PhD fellowship. A. R. R. P. thanks for the CNPq productivity fellowship.