Characteristics of a Two-Body Holonomic Constraint Mechanical System ()
1. Motivation and Goals
2. Physics of the Problem
Figure 1 shows the setup of the problem. Two identical blocks are connected with a massless, unstretchable line of length 2ℓ. Block 2 rests on the frictionless horizontal table top and the second one, block 1, is held horizontally along the extension of the line, equidistance from the edge. Conveniently the origin of the coordinate system is set as shown, with the vertical axis downward. At any given instance the coordinates of the blocks are, (x2(t),0) and (x1(t),y1(t)), respectively.
Block 1 is released from rest, as it falls pulls on block 2. The falling block sets a time-dependent tension, T(t), in the line. The massless line holds the same tension in the line. Tension, T, and angle, θ, with vertical are shown.
Applying Newton’s law gives the equations of motion for the blocks,
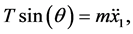 (1)
(1)
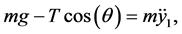 (2)
(2)
And
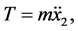 (3)
(3)
The holonomic constraint is formulated as,
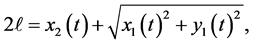 (4)
(4)
From Equations (1) and (3) and substituting for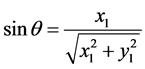 , we deduce,
, we deduce,
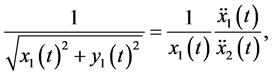 (5)
(5)
On the other hand from Equations (2)-(4) and substituting for
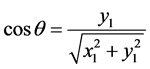
we have,
 (6)
(6)
Equation (6) depends only to the coordinates of block 1.
By the same token Equation (5) is reduced to the coordinates of the block 1 provided 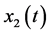 is replaced applying constraint Equation (4),
is replaced applying constraint Equation (4),
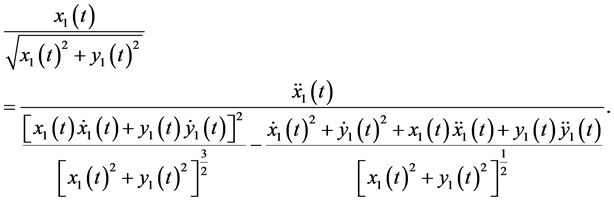 (7)
(7)
Now Equation (7) depends only on the coordinates of block 1.
Equations (6) and (7) form a set of coupled ordinary differential equations. Hopelessly we were unable to solve the set of Equations (6) and (7) analytically. We apply Mathematica’s numeric solver NDSolve; we were stunned with its power! Coordinates of the blocks are shown in Figure 2.
For practical reasons the half-length of the line is set ℓ = 1.0 m. Because the blocks are identical, derived equations are mass independent. To set the time
![]()
Figure 2. Coordinates of block 1 and 2 vs. t. The dashed, and gray lines are x1(t), y1(t); the solid black line is the x2(t).
scale we apply the free-fall run-time, namely .
.
The run-time of the actual case not being a free fall is a bit longer. Figure 2 is the display of the coordinates of the blocks vs. time. Accordingly, as intuitively expected, block 2, the one that slides on the table (solid curve) reaches the edge first; this figure confirms our intuition. At the beginning blocks are one meter away from the edge; their distances change and coordinates as shown change accordingly. Block 1 lags behind, so that when block 2 is at the edge, block 1 is not quite there. The length of the line is 2.0 m; the end tip of the solid gray curve is not quite 2.0 m showing the connecting line is not perfectly vertical.
By eliminating parameter t between the coordinates of block 1, it enables us to display its trajectory shown in Figure 3.
As shown in Figure 3 by the end of the run-time block 1 horizontally is off from the edge of the vertical leg and has fallen 1.8 m. Another interesting geometrical quantity is the time-dependent profile of the θ(t). The plot of this func-
tion, 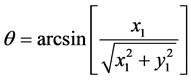 , vs. t is shown in Figure 4.
, vs. t is shown in Figure 4.
![]()
Figure 4. Display of orientation of the hanging line with respect to vertical position, i.e. θ, vs. t.
As shown, θ, begins at 90˚ and at the end of run-time plunges to about 11˚.
Next we utilize the solutions evaluating kinematic quantities such as speed and acceleration of the individual block. These are displayed in Figure 5.
Figure 5(a) shows beyond a certain instance, say about 0.4 s, block 2 (solid) moves faster than block 1 (dashed). The same is true for their associated accelerations depicted in Figure 5(b). These are additional justifications quantifying why block 2 should reach the edge first.
Figure 6(a) is the vertical acceleration of block 1. Figure 6(b) is the tension vs. time.
As depicted the falling block begins with gravity acceleration, g, gains acceleration as it falls, Figure 6(a). Had we considered a simple pendulum scenario with a constant length pivoted at the edge, the acceleration of the block at the bottom would have been 2 g.
Applying Equation (1) we also depict the tension in the line, T; this is shown in Figure 6(b). For the sake of simplicity we assumed m = 1.0 kg. As shown the tension at the beginning is zero. While the block falls tension builds reaching to its maximum value, over valuing the static limit of 10.0 N by a factor nine.
We complete the analysis by displaying one of many phase diagrams, namely the plot of horizontal speed of block 1 vs. its horizontal coordinate, i.e. .
.
Figure 7 shows the falling block while at its farthest distance from the edge begins with a zero horizontal speed reaching its maximum speed at closest distance to the edge.
![]()
![]() (a) (b)
(a) (b)
Figure 5. (a) is the plot of the horizontal speeds of the blocks; block 1 is dashed, block 2 is solid; (b) is the display of their associated accelerations.
![]()
![]() (a) (b)
(a) (b)
Figure 6. Vertical acceleration of block 1 (a) and tension (b) vs. time.
![]()
Figure 7. Phase diagram of horizontal speed of block 1 vs. its horizontal coordinate.
3. Conclusions and Suggestions
We analyze a problem that on its face is trivial. Although true, its detailed analysis is proven to be challenging. The challenge stems from the fact that the solution of the needed equations being a set of coupled super nonlinear ordinary differential equations analytically is unsolvable. This is another example that one needs to apply a Computer Algebra System (CAS). By applying one of the most powerful CASs, Mathematica, amazingly we were able to deduce the needed solutions. Having the solutions on hand, various information, e.g. trajectory of the falling object, dynamic quantities e.g. tension in the line is evaluated. For the majority of the quantities of interest we also applied the superb graphic capabilities of Mathematica displaying the results. An interested reader may extend the scope of the investigation considering 1) non-identical masses 2) determining masses making the blocks reach the edge simultaneously and 3) replacing the massless line with a massive one. Reference [6] embodies Mathematica codes and information needed to produce the graphs embedded in this article.