1. Introduction
A little over one hundred years ago, Niels Bohr [1] introduced the planetary model of the atom―with electrons revolving in circular orbits around a nucleus. Arnold Sommerfeld extended this model to include elliptic orbits [2] . The main contradiction of these models was―that in line with Maxwell theory the electron moving with acceleration in an electrostatic field of nucleus must emit electromagnetic waves, and thus loose energy. Bohr by passed this restriction by postulating the existence of certain special orbits, along which the electron can move without electromagnetic radiation, and introduced the action quantization rule for movement along these orbits. This postulate looked (and looks) insufficiently substantiated, and it has been rejected alongside the Bohr model, with onset of the era of wave mechanics.
Yet one more option has remained unanalyzed. Within the ambit of the classical Kepler problem, reducing electron’s angular momentum leads to the contraction of elliptic orbit―so at M à 0 the trajectory of the electron will aspire to a straight line.
At the point of maximum distance from the nucleus, the speed of the electron equals zero. This allows taking a new look at the radiation problem during electron’s accelerating movement in the field of nucleus. Preliminary estimates show that the action, A, made by the electron during movement at atomic distances has the order of a Planck constant, h. According to Max Planck’s classic quantum theory there exists a minimal value of action, h. So the action of the electron on the trajectory between two stationary points cannot not be less than h. Thus, condition A = h sets electron orbit parameters with a minimal distance from the nucleus. The electron moves in such an orbit with acceleration, nevertheless, it cannot emit radiation, because this would lead to reduction in its energy and speed, and thus reducing its action below minimum values practically possible.
This logical conclusion looks like the Bohr postulate on the existence of special orbits of an electron. Yet they differ essentially. While continuously moving in circular orbit, an electron gradually produces more and more action, and in excess of the minimum value (h) gains the ability to emit energy in the form of electromagnetic waves. The fact that this doesn't occur should certainly be postulated. In our model, movement happens between stationary points, while the lack of radiation is a direct consequence of its minimal action.
Reasoning in the same way, we reach a conclusion about the existence of a second orbit of an electron, and movement in such orbit between stationary points satisfies condition A = 2h. In this case the action A = h can transform into electromagnetic radiation, the “residual” action of an electron will be equal to the minimal value, i.e. h. Continuing with this line of reasoning, we reach a conclusion about the existence of a set of orbits of an electron in an atom meeting the general condition A = n * h. For single-electron systems (hydrogen-like atoms) the levels with n > 1 correspond to the excited states of atom. Experimental data show that the lifetime of such excited states many times exceeds the orbital period of the electron (see below for a more detailed explanation). This indicates a critical feature of the action of the Maxwell electromagnetic theory at the micro level. The imperative nature of its action peculiar to macro world, at the micro level is transformed to a probable one. An electron moving with acceleration and action exceeding the minimum value h generates a quantum of electromagnetic radiation only with a certain probability which is significantly smaller 1.
We can assume that the emission of a photon occurs at the time of passing of an electron at the minimum distance from a nucleus, the “over flight” of the nucleus, when the electron’s speed and acceleration reach maximum values. And there the absorption of a photon takes place. This mechanism permits to remove one more contradiction of the Bohr model which cannot explain how the electron skips from one orbit to another at the emission or absorption of a photon.
The electron which is at the maximum distance from a nucleus cannot absorb or emit a photon. It can be removed from its orbit mechanically, for example, after impact with an external electron or other particle, including collision with other atoms.
In conclusion, let’s discuss the problem of multielectron atoms, in which electrons settle into orbits which have various values of action. Though the probability of emission of a photon at the movement of an electron with A > h is very small, sooner or later it will occur, and as a result all electrons have to pass into an orbit with A = h. But as we know from experience, electronic configurations of multielectron atoms in their basic state are steady, and in the absence of external influences it is possible to speak, in principle, about their infinite stability. This can be explained through the operation of the following mechanism. A photon is emitted when an electron moving on a “far” orbit passes near a nucleus is absorbed by the electron moving on a “near” orbit and also being at this moment near a nucleus. As a result, these electrons seemingly exchange orbits, and at the same time the electronic configuration of the atom in general remains invariable.
The time which an electron spent near a nucleus is insignificantly small in comparison with the orbital period, and during this time the vector of speed changes the direction to the opposite. So, from a mathematical point of view the movement of an electron in such an orbit will be equivalent to the oscillation of an electron along the straight line connecting it to a nucleus with a perfectly elastic reflection from the nucleus. Here after for brevity’s sake we will speak about the oscillations of electrons.
2. Hydrogen Atom and Hydrogen-Like Atoms
Let’s now consider the motion of an electron in the nucleus field along the line connecting their centers. Since the masses of the nucleus and electron differ by three orders, it is possible to disregard the nucleus motion in the first approximation. Furthermore, we disregard the nucleus’s own dimensions and the ones of the electron, and treat them as material points.
According to Newton’s second law:
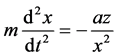
where x―distance to the nucleus, z?nuclear charge.
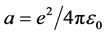
Multiply by dx/dt and integrate:
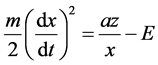
where E―integration constant, which has the dimension of energy.
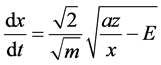 (1)
(1)
The action of the electron during movement from  to the nucleus (
to the nucleus (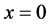 ):
):
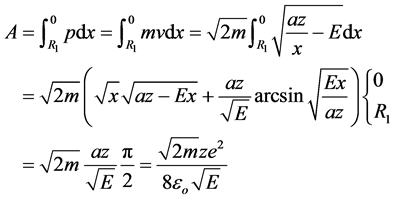 (2)
(2)
For the unidirectional oscillatory motion of the electron its action should be a divisible of h/2:
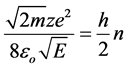
From this:
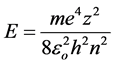 (3)
(3)
which coincides with the Bohr equation for the energy spectrum of an electron in a hydrogen-like atom.
Maximum distance of an electron from the nucleus is given by:
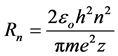 (4)
(4)
For the first level of the hydrogen atom R1 = 106 pm, which is twice the Bohr radius; and the same as the diameter of a hydrogen atom according to Bohr, which is logical for this method of calculation. In our model it’s meaningless to talk about the radius of the hydrogen atom, but for multielectron atoms the term acquires a clear physical meaning. Multielectron atoms possess the shape close to spherical one with the radius equal to the utmost limit of the electrons’ movement.
The equation of electron motion is obtained from the differential Equation (1). Separating the variables and integrating, we obtain:
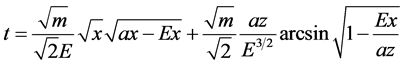 (5)
(5)
The half-period of oscillation we obtain substituting in (5) extreme values 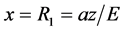 and
and :
:
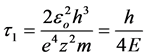
For the first level of the hydrogen atom this value equals 0.76 × 10−16 s.
In general case:
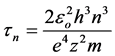 (6)
(6)
This implies that most of the time an electron is located near the border of the atom: one-third of the time in the range of (0.93 − 1)∙R1 and a half in the range of (0.84 − 1)∙R1. Similar with the approach of quantum mechanics, we can talk about the probability of finding the electron at a certain distance from the nucleus.
On the other hand, the location of the electron can be characterized by some average distance from the nucleus:
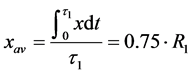 (7)
(7)
This ratio can prove useful in calculating the characteristics of atoms and molecules because it permits approximation of some electrons in an atom or an atom in the whole by a “static” model, in which electrons are located at some fixed distances from the nucleus.
The phase of maximum distance from the nucleus is also very interesting. Rn~n2, τn~n3. From this it follows that the electron in highest excited levels is located very far away from the nucleus and for an extremely long time, as compared to the basic level. If we monitor such an electron, we can easily take it for a free electron that is not associated with any particular atom, moving with a slow speed and exchanging energy with other “free” electrons. And suddenly this electron takes off and begins to move with ever-increasing speed to its “own” nucleus; then pushes away from it, and after some time again goes into a “free” movement state. It seems to us that this physical picture is very similar to the quantum entanglement.
3. Helium Atom and Two-Electron (2e) Atoms
The stable oscillations of two electrons must be synchronized. There are two possible modes of oscillations: symmetric, when the electrons are moving simultaneously to/from the nucleus; and asymmetric, in which the location of one electron near the nucleus corresponds to the maximum distance from the nucleus of the second electron.
For symmetric oscillations of two electrons in 2e-atoms:

The problem is solved in explicit form:
 (8)
(8)
![]()
Hence, for helium and 2e?atoms we have: an atom radius![]() , where RH?the radius of the hydrogen atom, z?the nuclear charge;
, where RH?the radius of the hydrogen atom, z?the nuclear charge;
Energy of an electron, in eV, ![]() , where 13.596 eV? energy of electron detachment from the lowest level of the hydrogen atom.
, where 13.596 eV? energy of electron detachment from the lowest level of the hydrogen atom.
The energy of the system, consisting of two electrons (energy of 2e-atom), equals to:
![]()
The energy required for the detachment of the first electron, or the first ionization potential, I1 = E2 − E1, where E1?the energy of a corresponding hydrogen-like atom, E1 = 13.596 z2.
For helium we have E2 = 83.24 eV, I1 = 28.83 eV, which exceeds the experimental data by 5.4% and 17.2%, respectively. With increasing nuclear charge deviation from the literature data decreases and for neon, for example, it is +1.0% and + 2.2% respectively.
Evaluation of electrons’ energy at the asymmetric oscillations gives the following values for helium: E2 = 90.44 eV, I1 = 36.03 eV, which is higher than the experimental data by 14.5% and 46.5%, respectively.
Thus, an option of the symmetric oscillations looks preferable. In general, the proposed model of the atom can be called pulsing. Most of the time the electrons are located on the periphery of the atom, periodically they simultaneously rush to the nucleus, the atom rapidly compresses and immediately decompresses, i.e. pulsates.
The accurate solution of the differential equation can be obtained for two-electron atoms. In principle, this can be done also for multielectron systems, but it generates some difficulties and inconveniencies. Therefore, below we have used numerical solution methods.
4. Multielectron Atoms
Only two electron scan occupy the first energy level. Perhaps in the future it will be possible to justify this statement, yet we accept it as given, as a postulate― which follows from the totality of experimental data on the structure of atoms.
Thus, all the electrons of the atoms of the second period, with the exception of two electrons, are in the second energy level, for which A = 2∙h.These electrons make synchronous symmetric oscillations, that is, have the same oscillation frequency, and approximately the same energy and the same range of oscillations (see below).In the proposed model there is no reason for the separation to s- and p-electrons, and all electrons of this energy level are equivalent.
To calculate the energy of an electron in a multielectron atom of the second period of the Periodic table we have used the equation:
![]() (9)
(9)
where![]() ―the energy of an electron in the second level containing j electrons;
―the energy of an electron in the second level containing j electrons;
![]() ―energy of interaction of the electron with other electrons of the second level;
―energy of interaction of the electron with other electrons of the second level;
![]() ―energy of interaction of the electron with the first level electrons.
―energy of interaction of the electron with the first level electrons.
The calculation algorithm is as follows.
In the first step we calculate the energy of interaction between the outer electrons, which depends on their relative position. It is convenient to characterize this interaction by parameter![]() , so that
, so that![]() .
.
Assessment of the interaction energy with the first level electrons is carried out using a static model with an arrangement of these electrons at a distance of 0.75∙R1 from the nucleus and their approximating by a sphere with a charge of −2. Then, in accordance with the laws of electrostatics we can divide the integral (9) into two:
![]() (10)
(10)
where R1―radius of the first shell. Calculations showed that the R1 value is not dependent on the presence and the number of electrons at the second level, and coincides with the value R1 of the corresponding helium-like (2e) atom. Substituting the values ![]() and R1 into Equation (10), we find numerically the value
and R1 into Equation (10), we find numerically the value ![]() and the value R2corresponding to it.
and the value R2corresponding to it.
In the second step we calculate the energy of the first level electrons, which unlike the radius depends on the number and location of the electrons at the outer level. Here again we use the static model and approximate the outer electrons by a sphere with radius 0.75∙R2 and a charge ?j. Calculations are carried out according to the equation, which is a combination of (9) and (10):
![]()
where![]() .
.
In the third step, we calculate the total energy of (je, 2e)-atom:
![]()
In the fourth step, we calculate the ionization energy of (je, 2e)-atom, or (n ? j + 1)-the atom’ stepwise potential containing n electrons on the filled outer level.
![]()
This is to say, we avoid adiabatic approximation and assume that the energy state of the inner level electrons also changes in the ionization process. The ionization energy is calculated as the energy difference between the “equilibrium” states of the atom.
The main uncertainty in this model arises from the choice of mutual spatial arrangement of electron orbits―an electron configuration. A configuration with the maximum possible distance between the electrons looks natural, since it provides a minimum energy of electron repulsion and thus a minimum of the potential energy of the atom. E.g., for 4, 6 and 8 electrons such optimal configurations are the tetrahedron, the octahedron and the cube, respectively. However, calculation of ionization energy potential of various atoms for such configurations shows substantial differences from the published (experimental and theoretical) data.
We have considered various options for the location of the electrons in space. The best results were obtained with a cubic system: eight cells are located in the corners of a cube and electrons consistently fill them with the formation of the following configurations.
This approach may look rather artificial: but, firstly, it is very similar to the ideas of Gilbert Lewis [3] and Irving Langmuir [4] about the structure of electron shells. Secondly, if we look at the configuration with five electrons, we see something like today’s accepted configuration for the nitrogen atom―with two paired s-electrons and three unpaired p-electrons, and so on. Of course, this scheme is very idealized and in reality these configurations may be highly distorted (even beyond recognition), but it is useful, in particular, to consider chemical bonding.
When analyzing the configurations presented in Figure 1 we see that the electrons there are not equivalent (beside 2 and 8 electrons configurations), in particular, they have different energies of interaction with neighboring electrons. On the other hand, in the proposed model of a pulsing atom, all the electrons on the same shell should oscillate with the same frequency, i.e. should be equivalent in this sense. This can be achieved by assigning different energy to different electrons and, accordingly, a different radius of orbit. But in this case different electrons will produce different actions during one movement cycle. How will this affect the action quantization rule? We propose to use here the principle of summed action: in a system of interacting particles the summed action of particles is quantized. This is in tune with Planck’s idea of quantization in the system of interacting resonators [5] . As for calculations, this principle permits to use average energy of electron repulsion and characterize the electrons on the same shell by the average energy values and the radius of their orbit - which greatly simplifies the calculations. It should be noted that differences in the characteristics of different electrons in the atom are not as great as they might seem at a first glance at the electron configuration. For example, for nitrogen atoms, the half-period of oscillations of outer shell electrons equals 25.52 × 10−18 s, average energy-78.31 eV, radius of the orbit-85.5 pm. Each electron has the energy of 76.08, 78.34, 78.34, 78.34, and 80.40 eV with the orbit radius 84.3, 85.5, 85.5, 85.5, and 86.6 pm, correspondingly, that is, the deviation from the average values does not exceed 3% for energy and 1.5% for radius.
![]()
Figure 1. The order of filling of the second electron shell of an atom.
We have calculated the total energy of the electron shells of all the elements of the second period of the Periodic table for different configurations of shells. Their deviation from published values does not exceed 1%. For ionization potentials (Table 1) the discrepancy from the published data is much higher, but overall is quite acceptable. We note also that the ionization potential is calculated as the difference between two large numbers, e.g., the first ionization potential of neon is only 0.5% of the total energy of the electron shell, so the error in its calculation must be inevitably large.
5. Conclusions
Thus, the proposed model of a pulsing atom can be summarized in the following theses.
1) An electron in an atom is considered as a material object moving along a particular trajectory.
2) The trajectory of the electron’s motion is an ellipse with a minor semiaxis, tending towards zero. From a mathematical point of view the movement through such an orbit is equivalent to oscillation with a perfectly elastic repulsion from the nucleus.
3) At the point of maximum distance from the nucleus the speed of the electron drops to zero (stationary point). This distance corresponds to the major semiaxis of the elliptic trajectory. We call this the radius of the orbit. For outer shell electrons this is equivalent to the radius of the atom.
4) The action produced by electrons in movement between stationary points is discrete and proportional to a Planck constant, A = n∙h, where ![]() This condition sets the allowable values of the electron energy and the radius of their orbit.
This condition sets the allowable values of the electron energy and the radius of their orbit.
![]()
Table 1. The calculated ionization potentials (in eV) of the atoms of the second period of the Periodic Table and their deviation from the literature [6] values (in%).
5) An electron moving in an orbit with A = h, does not emit electromagnetic waves. When moving in orbits with A > h, the emission of a photon is possible, and it occurs at the maximum speed of an electron’s motion, near the nucleus. Emission is probabilistic in nature. A photon emitted by an electron can be absorbed by another electron which is also moving close to the nucleus.
6) Most of the time the electron is located on the periphery of the orbit (the atom), and periodically rushes to the nucleus and rebounds back. The average distance of the electron from the nucleus is 0.75∙R, where R―radius of the orbit. The frequency of oscillation of the electron is of the order of 1016 Hz.
7) Electrons in multielectron atoms are located on the electron shells corresponding to A = n∙h, where ![]() It is postulated that the first shell can be occupied by 2 electrons, the second―by 8 electrons, etc.
It is postulated that the first shell can be occupied by 2 electrons, the second―by 8 electrons, etc.
8) Electrons on the same shell perform symmetric synchronous oscillations.
9) The frequency of their oscillation is the same, and in this sense all the electrons on one shell are equivalent. Separation into s-, p-, etc., electrons is excluded.
10) To calculate the energy of multielectron atoms, the principle of summed action is used: in a system of interacting particles the summed action of particles is quantized.