Optimisation of Effective Design Parameters for an Automotive Transmission Gearbox to Reduce Tooth Bending Stress

Mehmet Bozca

Machine Design Division, Mechanical Engineering Faculty, Yildiz Technical University, Istanbul, Turkey.

DOI: 10.4236/mme.2017.72004                

Abstract

Optimisation of effective design parameters to reduce tooth bending stress for an automotive transmission gearbox is presented. A systematic investigation of effective design parameters for optimum design of a five-speed gearbox is studied. For this aim contact ratio effect on tooth bending stress by the changing of contact ratio with respect to pressure angle is analysed. Additionally, profile modification effects on tooth bending stress are presented. During the optimisation, the tooth bending stress is considered as the objective function, and all the geometric design parameters such as module, teeth number etc. are optimised under two different constraints, including tooth contact stress and constant gear centre distance. It can be concluded that higher the contact ratio results in a reduced tooth bending stress, while higher the pressure angle caused an increase in tooth bending stress and contact stress, since decreases in the contact ratio. In addition, application of positive profile modification on tooth reduces tooth bending stress. All of the obtained optimum solutions satisfy all constraints.

Keywords

Optimisation, Gears, Pressure Angle, Contact Ratio, Bending Stress, Contact Stress

1. Introduction

The purpose of this study is optimisation of effective design parameters to reduce tooth bending stress for an automotive transmission gearbox.

Gears are mechanically transmitted power in automotive transmissions. Therefore, determining the geometric design parameters of gears is crucial.

By optimising all the geometric parameters of the gears, obtaining desired gearbox structures can be possible.

All constraints are also satisfied by the optimised geometric design parameters, based on pressure angle.

By optimising the effective geometric design parameters of the five-speed gearbox, such as the module, number of teeth, etc., reducing the tooth bending stress is possible.

Increasing the contact ratio results in reduced tooth bending stress and tooth contact stress. However, increased the pressure angle causes increasing of the tooth bending stress and tooth contact stress, since the contact ratio reduces depending on increasing of the pressure angle. Furthermore, higher contact ratio has a positive effect on reducing tooth bending stress. In contrast, higher pressure angle has a negative effect on reducing tooth bending stress. Application of tooth profile modification has a positive effectiveness on reducing the tooth bending stress.

The following discussion summarises findings from the literature:

1.1. Literature Review

The following results on tooth bending strength are presented in the literature:

An asymmetric gear pair improves the tooth-root bending load carrying capacity of the pinion and wheel gear at higher pressure angles on the coast side compared to a conventional symmetric gear. The optimum profile shift values increases with an increase in the speed ratio and number of teeth in the pinion, and increasing the asymmetric factor and pressure angles on the drive side improves the tooth-root bending capacity. When the speed ratio increases, the optimum maximum fillet stress increases very slightly compared to that of optimum profile shift factor for pinion [1] .

Asymmetric involute-type teeth were studied, since the non-involute teeth application has a number of disadvantages. The concept of one-sided involute asymmetric spur gear teeth is to increase the load carrying capacity of the driving involute. The literature concludes that the load carrying capacity can increase to 28% higher than that of standard 20˚ involute teeth [2] .

The advantage of using proposed asymmetric design in gearboxes is increased bending strength, pitting resistance, without changing the dimension or number of teeth in the gearbox [2] .

An alternative method to increase the tooth bending strength of involute gear teeth is positive modification of addendum (positive shifting) the pinion and, in some cases, mating wheel. This method produces well-running teeth, but both the pitting resistance and scoring resistance are reduced due to the positive shifting [2] .

A smaller pressure angle causes to produce undercut for a given number of teeth. However, the contact ratio increases, and load carrying capacity may be improved [3] .

Tooth profile modification is an effective parameter for optimising the geometric design parameters of gears. A numerical study found that the application of positive profile modification results in reduced tooth bending stress and increased safety factor for tooth bending stress [4] .

1.2. Gearbox Mechanism

The gearbox mechanism is shown in Figure 1. Where Z_1p, Z_2p, Z_3p and Z_4p denotes the 1^st speed pinion gear, the 2^nd speed pinion gear, the 3^rd speed pinion gear and the 4^th speed pinion gear respectively. Z_Cp and Z_Rp denote the constant speed pinion gear and the rear speed pinion gear. Z_g1, Z_g2, Z_g3 and Z_g4 denotes the 1^st speed wheel gear, the 2^nd speed wheel gear, the 3^rd speed wheel gear and the 4^th speed wheel gear respectively. Z_Cg and Z_Rg denote the constant speed wheel gear and the rear speed wheel gear. S₁, S₂ and S₃ denote synchronisers.

2. Effective Geometric Design Parameters

General definitions and specification factors for gears are given in DIN 868 as follows.

The module, m is the basic parameter for the linear dimensions of gear tooth systems. It is the result of dividing the pitch, p by the number π. The pitch is determined by the dimensions of the datum surface and the number of teeth; see Figure 2(a).

The number of teeth, z of a gear is the number of teeth present on the full circumference of the gear or the number that would be feasible for a chosen pitch; see Figure 2(b).

The face width, b, is the distance between the two end surfaces of the gear tooth system; see Figure 2(c).

The helix angle, β, is the angle between the helix line and horizontal axis; see Figure 2(d).

The centre distance, a, of a gear pair with parallel axes is the shortest distance between the two axes; see Figure 2(e).

Figure 1. Five-Speed manual gearbox with helical gear for automotive transmission.

(a) (b) (c) (d) (e)

Figure 2. Design parameters for a gearbox. (a) module; (b) number of teeth z; (c) facewidth b; (d) helix angle β; (e) centre distance a.

3. Contact Ratio

The dimensions of helical gear are shown in Figure 3 and the contact line is shown Figure 4. Obviously, tooth profiles must be proportioned such that a second pair of mating teeth comes into contact before the first pair is out of contact [5] .

If the gear contact ratio equal to 1, then one tooth is leaving contact just as the next is beginning contact. A unity contact angle is undesirable, because slight errors in tooth spacing will cause oscillations in velocity, and, subsequently, vibration, and noise. In addition, the load will be applied on the tip of the tooth, creating the largest possible bending moment [6] .

In general, the higher the contact ratio, the smoother the running of the gears. When a contact ratio is equal to 2 or more means that at least two pairs of teeth are theoretically in contact currently [5] .

If a profile contact ratio is lower than 2.0, is called as Low Contact Ratio (LCR), while gearing with this parameter equal to 2.0 or greater than 2.0 is called as High Contact Ratio (HCR) [5] .

The contact ratio consists of two parts, such as the transverse contact ratio, ε_α, and the overlap (face contact) ratio, ε_β.

3.1. Transverse Contact Ratio, ε_α

The contact ratio (CR) is defined as the average number of teeth in contact during the gear rotation. The transverse contact ratio, ε_α is calculated as follows [8] .

(1)

where g_α is the path length of the contact line [mm], and p_et is the base pitch [mm], d_a1 is the addendum circle diameter of the pinion gear [mm], d_b1 is the base circle diameter of the pinion gear [mm], d_a2 is the addendum circle diameter of the wheel gear [mm], d_b2 is the base circle diameter of the wheel gear [mm], a_d is the centre distance [mm], α_t is the transverse pressure angle [˚], and m_t is the transverse module [mm].

The addendum circle diameter of the pinion gear, d_a1, is calculated as follows [8] .

Figure 3. Contac line of helical gear.

Figure 4. Contac line of helical gear including contact length AE.

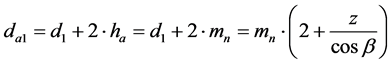(2)

where m_n is the normal module [mm], z is the number teeth [-], and β is the helix angle [˚].

The base circle diameter of the pinion gear, d_b1, is calculated as follows [8] .

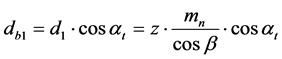(3)

The addendum circle diameter of the wheel gear, d_a2, is calculated as follows [8] .

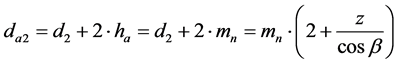(4)

The base circle diameter of the wheel gear, d_b2, is calculated as follows [9] .

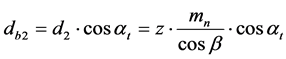(5)

The centre distance, a_d, is calculated as follows [8] .

(6)

3.2. Overlap Ratio, ε_β

The overlap ratio, ε_β is calculated as follows [8] .

(7)

where U is the action length [mm], p_t is the transverse pitch [mm], b is the face width [mm], and m_n is the normal module [mm].

3.3. Total Contact Ratio, ε_γ

The total contact ratio, ε_γ is calculated as follows.

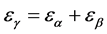(8)

where ε_α is the transverse contact ratio and ε_β is the overlap ratio. Helical gears have higher contact ratio than spur gears thus, they have also higher load carrying capacities than spur gears.

4. Strength of Helical Gears

The gear strength is defined by two criteria such as the tooth bending strength and tooth contact strengths according to the ISO 6336.

4.1. Tooth Bending Stress

The bending stress in distribution are shown in Figure 5. The real tooth-root stress, is calculated as follows [7] [8]

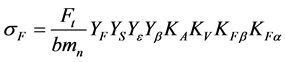(10)

The permissible bending stress, 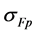, is calculated as follows [7] [8] .

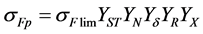(11)

where all the responsible parameters for the tooth bending stress are given in Table 1. The safety factor for bending stress 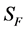is calculated as follows [7] [8]

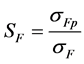(12)

Table 1. Tooth bending stress parameters.

Figure 5. Bending stress at the tooth root.

4.2. Tooth Contact Stress

The contact stress, distribution is shown in Figure 6. The real contact stress, is calculated as follows [7] [8]

(13)

The permissible contact stress, is calculated as follows [7] [8] :

(14)

where all the responsible parameters for the tooth contact stress are given in Table 2.

Table 2. Tooth contact stress parameters.

Figure 6. Contact stress at the tooth flank.

The safety factor for contact stress, , is calculated as follows [7] [8] :

(15)

5. Optimisation of Effective Design Parameters of Gearbox

Constrained optimisation method is helpful for designing light-weight gearbox structures. Constraints, including tooth contact stress and constant distance between gear centres can be used for this optimisation.

During optimisation, the aim is typically to minimise the cost of a structure while satisfying all the design requirements. By optimising the effective design parameters, a light-weight gearbox structure design is also possible [9] [10] .

5.1. Objectives Function

Tooth bending stresses are considered as objective functions, during the optimisation study. The flowchart of the optimisation procedure of geometric design parameters is shown in Figure 7. The following objective function was used:

(16)

Following minimum tooth bending stress is defined as objective function:

(17)

Thus, the module m, the number of teeth z, and the helix angle β, are the design parameters to be determined. During the constrained optimisation, the following optimisation problem is solved:

(18)

Subject to: and (19)

where LB is lower bound and UB is upper bounds on the design parameter vector. The iterations start with the initial values of design parameters such as, m_0, z₀, β₀, and b₀. Initial design parameters X0 are varied during the optimisation process, where G (X) ≤ 0 is the nonlinear inequalities.

Figure 7. Flow chart to optimise gearbox design parameters.

5.2. Constraint Functions

During constraint optimisation, the tooth contact stress and constant distance between gear centres are considered as the constraint function as follows:

(20)

where is the real contact stress [N/mm²] and is the permissible contact stress [N/mm²].

(21)

where a₁ is the centre distance of the 1^st speed, a₂ is the centre distance of the 2^nd speed, a₃ is the centre distance of the 3^rd speed, a₄ is the centre distance of the 4^th speed, a₅ is the centre distance of the 5^th speed and a_R is the centre distance of the rear speed.

6. Numerical Example

Constrained optimisation method is applied to the five-speed gearbox mechanism to reduce tooth bending stress. All optimisation programs are developed using MATLAB. The sequential quadratic programming (SQP) method is used.

Twenty-four design parameters are optimised simultaneously using the developed programs. All the parameters for the tooth strength calculation are shown in Table 1 and Table 2, respectively.

7. Results

It is observed in solution 1 (Table 3) that the obtained optimum effective parameters result in satisfied values for each speed. By considering safety factors, this solution is more acceptable for 1^st and rear speed. The safety factor for bending stress, S_F, ranges between 1.1797 and 3.1783, and the safety factor for contact stress, S_H, varies between 1.2269 and 2.5490.

It is observed in solution 2 (Table 3) that the obtained optimum effective parameters result in acceptable values for each speed. The safety factor for bending stress, S_F, ranges between 1.1254 and 3.0457, and the safety factor for contact stress, S_H, varies between 1.1854 and 2.4725.

The results from solution 3 (Table 3) show that the obtained optimum effective parameters satisfy desired requirements. By considering safety factors, this solution is more acceptable for 2^nd and 3^rd speed. The safety factor for bending stress, S_F, ranges between 1.0776 and 2.9275, and the safety factor for contact stress, S_H, varies between 1.1491 and 2.4046.

The results from solution 4 (Table 3) indicate that the obtained optimum effective parameters satisfy all requirements. The safety factor for bending stress, S_F, ranges between 1.0357 and 2.8229, and the safety factor for contact stress, S_H, varies between 1.1175 and 2.3448.

The results from solution 5 (Table 3) show that the obtained optimum solutions result in desired values. However, by considering safety factors, this solution is more acceptable for constant pinion. The safety factor for bending stress, S_F, ranges between 0.9993 and 2.7314, and the safety factor for contact stress, S_H, varies between 1.0901 and 2.2926.

(a) (b) (c) (d) (e) (f)

Table 3. (a) Optimisation results-Solution no 1; (b) Optimisation results-Solution no 2; (a) Optimisation results-Solution no 3; (d) Optimisation results-Solution no 4; (e) Optimisation results-Solution no 5; (f) Optimisation results-Solution no 6.

The results from solution 6 (Table 3) indicate that the obtained optimum values satisfy all requirements. However, by considering safety factors, this solution is more acceptable for 4^th speed. The safety factor for bending stress, S_F, ranges between 0.9680 and 2.6522, and the safety factor for contact stress, S_H, varies between 1.0667 and 2.2475.

From the obtained optimisation results, it can be concluded that increasing the contact ratio results in reduced tooth bending stress and reduced contact stress. Furthermore, increased the pressure angle caused increased the tooth bending stress and contact stress, by reducing the contact ratio. The relations between the contact ratio and bending stress are shown in Figures 8-13. The contact ratio and pressure angle relations are shown in Figures 14-19.

7.1. Contact Ratio and Tooth Bending Stress Relation

The contact ratio and bending stress relation for the 1^st speed is shown in Figure 8. As the contact ratio increases from 1.3862 to 1.7836, the bending stress reduces from 987.300 [N/mm²] to 822.2394 [N/mm²]. Thus, increasing the contact ratio 28.66% results in a 20.07% reduction in tooth bending stress.

The contact ratio and bending stress relation for the 2^nd speed is shown in Figure 9. As the contact ratio for the 2^nd speed increases from 1.4086 to 1.8255, the bending stress reduces from 817.7000 [N/mm²] to 679.0009 [N/mm²]. Thus, increasing the contact ratio 29.59% reduces the tooth bending stress 20.42%.

The contact ratio and bending stress relation for the 3^rd speed is shown in Figure 10. As the contact ratio for the 3^rd speed increases from 1.4150 to 1.8423, bending stress reduces from 836.2000 [N/mm²] to 692.3186 [N/mm²]. Thus, increasing the contact ratio 30.19%, results a 20.78% reduction in tooth bending stress.

The contact ratio and bending stress relation for the 4^th speed is shown in Figure 11. As the contact ratio for the 4^th speed increases from 1.4321 to 1.8895, the bending stress reduces from 680.0000 [N/mm²] to 558.4413 [N/mm²]. Thus, increasing the contact ratio 31.93% reduces the tooth bending stress 21.76%.

The contact ratio and bending stress relation for the 5^th speed is shown in Figure 12. As the contact ratio for the 5^th speed increases from 1.3970 to 1.7963, the bending stress reduces from 377.0000 [N/mm²] to 314.6310 [N/mm²]. Thus, increasing the contact ratio 28.58%, results in a 19.82% reduction in the tooth bending stress.

The contact ratio and bending stress relation for the rear speed is shown in Figure 13. As the contact ratio for the rear speed increases from 1.4295 to 1.8913, the bending stress reduces from 1033.1000 [N/mm²] to 847.6631 [N/mm²]. Thus, increasing the contact ratio 32.30%, reduces the tooth bending stress 21.87%.

Figure 8. Contact ratio and bending stress relation for the 1^st speed.

Figure 9. Contact ratio and bending stress relation for the 2^nd speed.

Figure 10. Contact ratio and bending stress relation for the 3^rd speed.

Figure 11. Contact ratio and bending stress relation for the 4^th speed.

Figure 12. Contact ratio and bending stress relation for the 5^th speed.

Figure 13. Contact ratio and bending stress relation for the rear speed.

7.2. Contact Ratio and Pressure Angle Relation

The contact ratio and pressure angle relation for the 1^st speed is shown in Figure 14. As the pressure angle for the 1^st speed reduces from 22 [˚] to 12 [˚], the contact ratio increases from 1.3862 to 1.7836. Thus, decreasing the pressure angle 83%, results in a 28.66% increase in the contact ratio.

The contact ratio and pressure angle relation for the 2^nd speed is shown in Figure 15. As the pressure angle for the 2^nd speed reduces from 22 [˚] to 12 [˚], the contact ratio increases from 1.4086 to 1.8255. Thus, decreasing the pressure angle 83%, increases the contact ratio 29.59%.

The contact ratio and pressure angle relation for the 3^rd speed is shown in Figure 16. As the pressure angle for the 3^rd speed reduces from 22 [˚] to 12 [˚], the contact ratio increases from 1.4150 to 1.8423. Thus, decreasing the pressure angle 83%, results in a 30.19% increase in the contact ratio.

The contact ratio and pressure angle relation for the 4^th speed is shown in Figure 17. As the pressure angle for the 4^th speed reduces from 22 [˚] to 12 [˚], the contact ratio increases from 1.4321 to 1.8895. Thus, decreasing the pressure angle 83%, result in increases the contact ratio 31.93%.

The contact ratio and pressure angle relation for the 5^th speed is shown in Figure 18. As the pressure angle for the 5^th speed reduces from 22 [˚] to 12 [˚], the contact ratio increases from 1.3970 to 1.7963. Thus, decreasing the pressure angle 83%, results in a 28.58% increase in the contact ratio.

The contact ratio and pressure angle relation for the rear speed is shown in Figure 19. As the pressure angle for the rear speed reduces from 22 [˚] to 12 [˚], the contact ratio increases from 1.4295 to 1.8913. Thus, decreasing the pressure angle 83%, results in a 32.30% increase in the contact ratio.

Figure 14. Contact ratio and pressure angle relation for the 1^st speed.

Figure 15. Contact ratio and pressure angle relation for the 2^nd speed.

Figure 16. Contact ratio and pressure angle relation for the 3^rd speed.

Figure 17. Contact ratio and pressure angle relation for the 4^th speed.

Figure 18. Contact ratio and pressure angle relation for the 5^th speed.

Figure 19. Contact ratio and pressure angle relation for the rear speed.

7.3. Tooth Profile Modification Factor and Bending Stress Relation

The tooth profile modification and bending stress relation for the 1^st speed is shown in Figure 20. While the profile modification factor increase from 0 to 0.3, the bending stress reduces from 1171.5000 [N/mm²] to 927.4486 [N/mm²].

The tooth profile modification and bending stress relation for the 2^nd speed is shown in Figure 21. As the profile modification factor increase from 0 to 0.3, the bending stress reduces from 854.7000 [N/mm²] to 712.5610 [N/mm²].

The tooth profile modification and bending stress relation for the 3^rd speed is shown in Figure 22. While the profile modification factor increase from 0 to 0.3, the bending stress reduces from 873.9000 [N/mm²] to 728.3622 [N/mm²].

The tooth profile modification and bending stress relation for the 4^rd speed is shown in Figure 23. As the profile modification factor increase from 0 to 0.3, the bending stress reduces from 709.5000 [N/mm²] to 591.5892 [N/mm²].

The tooth profile modification and bending stress relation for the 5^th speed is shown in Figure 24. As the profile modification factor increase from 0 to 0.3, the bending stress reduces from 394.4000 [N/mm²] to 328.8225 [N/mm²].

The tooth profile modification and bending stress relation for the rear speed is shown in Figure 25. As the profile modification factor increase from 0 to 0.3, the bending stress reduces from 1074.800 [N/mm²] to 899.1084 [N/mm²].

Figure 20. Profile modification factor and bending stress relation for the 1^st speed.

Figure 21. Profile modification factor and bending stress relation for the 2^nd speed.

Figure 22. Profile modification factor and bending stress relation for the 3^rd speed.

Figure 23. Profile modification factor and bending stress relation for the 4^th speed.

Figure 24. Profile modification factor and bending stress relation for the 5^th speed.

Figure 25. Profile modification factor and bending stress relation for the rear speed.

7.4. Optimum Design of Effective Parameters

A flowchart of the optimum design of effective parameters based on pressure angle is shown in Figure 26.

The safety factor for bending stress, S_F, and safety factor for contact stress S_H, are the basic selection criteria used by the Optimum Design. The Selective Optimum Design is shown in Table 4.

Although, obtained optimised geometric design parameters are significant for all constraints, the best solutions, based on pressure angle are determined from the obtained optimum solutions for each speed.

The geometric design parameters are optimised simultaneously for each given gearbox speed. However, it is not necessary to choose a single solution that changes with respect to the pressure angle. Therefore, all effective geometric design parameters can be determined independently for each speed from obtained optimum solutions.

Figure 26. Flowchart of optimum design of effective parameters.

Table 4. Determination of best optimum solution.

8. Conclusions

Optimisation of effective design parameters to reduce tooth bending stress for an automotive transmission gearbox is presented. The tooth bending stress is considered as the objective function, and the geometric design parameters are optimized under two different constraints. Tooth contact stress and constant distance between gear centres are considered as the constraints function. During optimization study, pressure angles were varied, thus contact ratios were also changed with respect to the pressure angle. The effect of the contact ratio on the tooth bending stress is analysed, and the following conclusions are drawn:

By optimising the effective geometric design parameters of the five-speed gearbox, such as the module, number of teeth, etc., reducing the tooth bending stress is possible.

Increasing the contact ratio results in reduced tooth bending stress and tooth contact stress. However, increased the pressure angle causes increasing of the tooth bending stress and tooth contact stress, since the contact ratio reduces depending on increasing of the pressure angle. Furthermore, higher contact ratio has a positive effect on reducing tooth bending stress. In contrast, higher pressure angle has a negative effect on reducing tooth bending stress. Application of tooth profile modification has a positive effectiveness on reducing the tooth bending stress.

Increasing the contact ratio 28.58% - 32.30%, results in a 19.82% - 21.87% reduction in tooth bending stress. In contrast, decreasing the pressure angle 83%, increases the contact ratio 28.58% - 32.30%. Gears with having higher contact ratio, have higher load carrying capacities.

Although, all the determined optimised geometric design parameters satisfy all constraints, it is not necessary to choose a single solution that changes with respect to the pressure angle.

All effective geometric design parameters can be determined independently for each speed inside the obtained optimum solutions. Based on pressure angle, the best optimised solutions are determined from the obtained optimum solutions for each speed in five-speed gearbox.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kumar, V.S., Muni, D.V. and Muthuveerappan, G. (2008) Optimization of Asymmetric Spur Gear Drives to Improve the Bending Load Capacity. Mechanism and Machine Theory, 43, 829-858.
[2]	Costopoulos, T. and Spitas, V. (2009) Reduction of Gear Filet Stresses by Using One-Sided Involute Asymmetric Teeth. Mechanism and Machine Theory, 44, 1524-1534.
[3]	Marimuthu, P. and Muthuveerappan, G. (2016) Design of Asymmetric Normal Contact Ratio Spur Gear Drive through Direct Design to Enhance the Load Carrying Capacity. Mechanism and Machine Theory, 95, 22-34.
[4]	Pedrero, J.I., Pleguezuelos, M. and Munoz, M. (2011) Contact Stress Calculation of Undercut Spur and Helical Gear Teeth. Mechanism and Machine Theory, 46, 1633-1646.
[5]	Bozca, M. and Dikmen, F. (2012) Optimisation of Geometric Parameters of Gears under Variable Loading Condition. Advanced Materials Research, 445, 1005-1010. https://doi.org/10.4028/www.scientific.net/AMR.445.1005
[6]	Juvinall, R.C. and Marshek, K.M. (2006) Fundamentals of Machine Component Design. John Wiley & Sons, Inc., Hoboken.
[7]	Naunheimer, H., Bertsche, B., Ryborz, J. and Novak, W. (2011) Automotive Transmissions. Springer-Verlag, Berlin Heidelberg. https://doi.org/10.1007/978-3-642-16214-5
[8]	Roloff/Matek (2005) Maschinenelemente, Vieweg and Sohn Verlag. GWV Fachver-lage GmbH, Wiesbaden.
[9]	Bozca, M. (2010) Torsional Vibration Model Based Optimization of Gearbox Geometric Design Parameters to Reduce Rattle Noise in an Automotive Transmission. Mechanism and Machine Theory, 45, 1583-1598.
[10]	Bozca, M. and Fietkau, P. (2010) Empirical Model Based Optimization of Gearbox Geometric Design Parameters to Reduce Rattle Nose in an Automotive Transmission. Mechanism and Machine Theory, 45, 1599-1612.