1. Introduction
String Theory is an ambitious project which starts from the assumption (among other things) that elementary particles can be understood as rotating strings, and it aims at a complete description of fundamental physics, including general relativity.
The present paper is not about string theory, but rather in a certain sense investigates an implication in the other direction: starting from general relativity, is there a good way to motivate why rotating strings should be more natural models for elementary particles than, say, spherical particles or point-particles?
The first question is of course: what should “natural” refer to in this context? A possible hint can be given by an analogy with mechanics: In statics, there is an old and well-known principle which asserts that the most “natural” state, and the one which will actually occur, is the one which minimizes the energy. In general relativity, the presence of mass-energy manifests itself through non-zero curvature, thus it could be argued that in the four-dimensional statics of space-time, the most natural states are the ones which minimize curvature.
Although other view-points are possible, I will in the following interpret this as minimizing the integral
 (1.1)
(1.1)
where  is the scalar curvature. It should be noted that the use of the word “minimizing” here is essential: it is not equivalent to looking for stationary solutions as the traditional theory usually does. This minimizing principle could be further motivated (and be made more precise) starting from an analogy with Feynmann’s principle of “democracy of all histories” (see [1] ). But this is in fact a complicated question, so it will be discussed elsewhere (see however [2] [3] ).
is the scalar curvature. It should be noted that the use of the word “minimizing” here is essential: it is not equivalent to looking for stationary solutions as the traditional theory usually does. This minimizing principle could be further motivated (and be made more precise) starting from an analogy with Feynmann’s principle of “democracy of all histories” (see [1] ). But this is in fact a complicated question, so it will be discussed elsewhere (see however [2] [3] ).
In any case, minimizing (1.1) leads to interesting and difficult mathematical problems. In particular, it pin-points an unexpected difference between Euclidian geometry and Lorentz geometry.
The starting point for the study in this paper will be an extremely simple model for a particle: let us simply assume that the particle is defined by the region in space which it occupies. But in addition it can be noted that somewhere inside or close to the particle, the Ricci tensor should in general be different from zero if the resulting metric is to agree with a non-trivial Schwarzschild metric far away from the particle. For instance, if we consider the case of a spherically symmetric metric, then an elementary computation shows that no non-trivial, non-singular such metric will have vanishing Ricci tensor.
Exactly what this deviation from the Schwarzschild geometry looks like is something which a complete theory of elementary particles should be able to tell us, but we are not there yet. General relativity can not really help us either; even if we could in principle attempt to solve the field equations inside the particle, this would inevitably have to make use of so far unmotivated assumptions about matter, and also would require the use of the theory of general relativity in a situation where it has very little support.
An alternative approach, one which is close the the spirit of this paper, is to consider the metric inside the particle to be unknown, but nevertheless try to find general properties of all such metrics. Thus, we are led to a purely mathematical problem and, as it seems, to a difficult one.
In this paper, I will only attempt to achieve partial results. Thus, consider a string-shaped region in three-space (for a more precise definition, see Section 2). Far away from this region, one can expect the metric to be close to the Schwarzschild metric, and in particular to have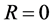 . In view of this and the extrem weakness of the gravitational force, I will, at least to start with, completely neglect any deviation from flat space-time outside the defining region of the string itself and only consider deformations of the metric inside this region. Thus, the only way the Schwarzschild metric comes in is to motivate why the curvature in general should be non-zero inside, but all other influences are discarded. For reasons to be discussed elsewhere (see however Section 2), the case where these deformations are located near the ends of the string is of particular interest.
. In view of this and the extrem weakness of the gravitational force, I will, at least to start with, completely neglect any deviation from flat space-time outside the defining region of the string itself and only consider deformations of the metric inside this region. Thus, the only way the Schwarzschild metric comes in is to motivate why the curvature in general should be non-zero inside, but all other influences are discarded. For reasons to be discussed elsewhere (see however Section 2), the case where these deformations are located near the ends of the string is of particular interest.
Given such a string in an otherwise flat three-space, we can ask what will happen if we add a time-coordinate and let the string perform motions. In particular, we may study the case of a rotating string and ask what speed of rotation of the string will minimize the curvature in the sense of (1.1).
It may seem intuitively obvious that the behavior which generates the least four-dimensional curvature should be to assume the string to stay at rest for all times. And indeed this appears to be what happens in Euclidian geometry. What is curious however, is that this does not seem to be what happens in the case of Lorentz geometry: rotating strings may have lower curvature than non-rotating ones.
It should be said right away that from a four-dimensional, relativistic perspective, such rotations must of course involve the time-coordinate in a non-trivial way. And in general, rotation in general relativity is a complicated concept (see e.g. [4] and also the discussion in Section 5). In the following, I will only make use of a very simplified kind of rotation which essentially neglects changes in the time coordinate. This defect should be kept in mind when considering the numerical computations with high-speed rotations below. On the other hand, in the main theorem this draw-back plays no essential role, since there the aim is to prove that non-rotating strings are not curvature minimizing, and for this purpose any kind of rotation which makes the curvature smaller, physically plausible or not, will do. In addition, the main theorem is concerned with infinitesimal speed of rotation, in which case the essentially classical rotations used here may be considered to be rather natural. To describe the kind of rotation which actually minimizes the curvature when the speed of rotation is not small, seems to be a much harder problem which I will not attempt to solve here.
After some introductory definitions in Section 2, I proceed in Section 3 to give a few numerical examples computed by Mathematica to give a feeling for what may happen. In this case, I also consider high-speed rotations, even if this means that one should be careful when drawing conclusions. As it seems, the general behavior is rather independent of the exact form of the metric inside the string; all examples indicate a similar behavior where the minimum of the curvature is assumed when the ends of the string rotate with (approximately) the speed of light.
In Section 4, I state and prove the best I can do rigorously: the main Theorem 1 can be expressed by saying that for any metric with certain specific symmetry properties and which is close to the flat one, the non-rotating case is not curvature minimizing in the sense of (1.1). In fact, what is proved is that for the special kind of rotation considered here, the case of zero angular velocity gives a local maximum for (1.1), rather than a minimum. As a contrast, Theorem 2 states that in the case of Euclidian geometry we really do have a local minimum.
As is not uncommon in differential geometry, the computations of curvature involved tend to be very lengthy. Although it may in fact be possible to carry them out by hand, I have used Mathematica for this purpose. The reason is that even if one could do it all without computers, the amount of work is so large that human errors are almost impossible to avoid. However, the use of Mathematica is restricted to the symbolic part, i.e. the computation of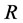 . When it comes to computing the integral in (1.1) in the theorems, this part can be made by hand, so no approximate methods are involved here. In general, I’m indebted to [5] for the use of tensor calculus with Mathematica.
. When it comes to computing the integral in (1.1) in the theorems, this part can be made by hand, so no approximate methods are involved here. In general, I’m indebted to [5] for the use of tensor calculus with Mathematica.
In Section 5 finally, I discuss possible further developments. Let me also again emphasize that I do not in this paper make any claims about actual string theory. String theory is a quantum mechanical theory, and it is not at all clear what a corresponding quantum treatment of this problem would lead to. Nevertheless, I do think that the topic of this paper has got something important to say about Lorentz geometry on the microscopic level and, as a consequence, may contribute to our understanding of the connection between general relativity and quantum mechanics.
2. Rotating Classical Strings
The strings in this paper will not be considered to be strictly one-dimensional, but rather to be three-dimensional objects which can however be arbitrarily thin. The precise definition will be to let the string be the convex hull of two balls  and
and 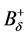 with radius
with radius 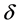 and centers at some points
and centers at some points 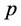 and
and , where
, where 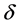 is a strictly positive number. Outside this region, the metric is assumed to be completely flat.
is a strictly positive number. Outside this region, the metric is assumed to be completely flat.
To get a model for a string, rotating around an axis perpendicular to the string itself, let us now for definiteness put  and
and 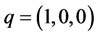 at time
at time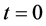 , and for arbitrary
, and for arbitrary 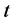 suppose the string to be the convex hull of the balls
suppose the string to be the convex hull of the balls 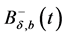 and
and 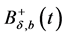 with centers at
with centers at  and
and
 . In addition, the metric should satisfy an obvious time invariance property in the sense that pull-back by the time-translation map equals rotation by the corresponding angle.
. In addition, the metric should satisfy an obvious time invariance property in the sense that pull-back by the time-translation map equals rotation by the corresponding angle.
Finally, we suppose that whatever it is that generates mass, it is located at the ends of the string, i.e. within ![]() and
and![]() . Certainly, other models are possible, but nevertheless this seems like a natural starting point. In particular, it appears that strings with a more evenly spread distribution of curvature would share the same general properties as the ones studied here, except for the speed of the rotation at the ends of the string which may no longer be close to the speed of light.
. Certainly, other models are possible, but nevertheless this seems like a natural starting point. In particular, it appears that strings with a more evenly spread distribution of curvature would share the same general properties as the ones studied here, except for the speed of the rotation at the ends of the string which may no longer be close to the speed of light.
3. Some Numerical Examples of Rotating Strings
Consider the following metric: let ![]() be a function defined for
be a function defined for ![]() with continuous derivate, piecewise continuous second derivative, and which is equal to 0 for
with continuous derivate, piecewise continuous second derivative, and which is equal to 0 for![]() , where
, where![]() . In addition, in order for the metric below not to give singular contributions to the curvature, it is important to note that
. In addition, in order for the metric below not to give singular contributions to the curvature, it is important to note that ![]() (and we also assume that
(and we also assume that![]() , although a weaker condition would suffice). Small values of
, although a weaker condition would suffice). Small values of ![]() correspond to thin strings and large values to thick ones. In the following, the exact value of
correspond to thin strings and large values to thick ones. In the following, the exact value of ![]() is not important so for the rest of this section I put
is not important so for the rest of this section I put![]() .
.
Next, put
![]() (3.1)
(3.1)
Clearly, this function is now defined on ![]() and sufficiently regular for the following metric to make good sense:
and sufficiently regular for the following metric to make good sense:
![]() (3.2)
(3.2)
We note that it coincides with the ordinary Minkowski metric outside the rotating string, in fact outside the balls ![]() and
and![]() . In the following,
. In the following, ![]() should in general be thought of as small numbers. However, to illustrate the basic mechanism, I have in this section chosen to work with
should in general be thought of as small numbers. However, to illustrate the basic mechanism, I have in this section chosen to work with![]() .
.
Using Mathematica, one may now attempt to compute numerically the integral of ![]() per unit of time for different choices of
per unit of time for different choices of![]() , which, in view of the obvious time-homogeneity, equals the integral over
, which, in view of the obvious time-homogeneity, equals the integral over ![]() for
for![]() :
:
![]() (3.3)
(3.3)
where I have used the notation ![]() for the three-dimensional volume measure on the hypersurface
for the three-dimensional volume measure on the hypersurface![]() .
.
In Figure 1, I have plotted ![]() as a function of the speed of rotation
as a function of the speed of rotation ![]() with three different simple choices for
with three different simple choices for![]() : in the first case,
: in the first case, ![]() is positive, in the second it takes both positive and negative values, and in the last example it is purely negative. The plots are remarkably similar for different choices of
is positive, in the second it takes both positive and negative values, and in the last example it is purely negative. The plots are remarkably similar for different choices of![]() . In fact, in all cases we get a function which takes its global minimum when the centers of the balls
. In fact, in all cases we get a function which takes its global minimum when the centers of the balls ![]() and
and ![]() move with approximately the speed of light (
move with approximately the speed of light (![]() ). If we would normalize the graphs by instead considering
). If we would normalize the graphs by instead considering
![]() , all three graphs would be essentially indistinguishable.
, all three graphs would be essentially indistinguishable.
Of course, the graphs in Figure 1 are only examples. And in fact even for the very simple choices above for the metric, the computations seem to be close to the limit of what Mathematica can handle on an ordinary MacBook, hence should be judged with a certain care. For the sake of completeness: the three functions plotted are![]() ,
, ![]() and
and
![]() , with
, with ![]() and the three fourth degree polynomials
and the three fourth degree polynomials
![]() (a) (b)
(a) (b)
Figure 1. (a) three different choices for![]() . (b) the graphs of the corresponding functions
. (b) the graphs of the corresponding functions![]() .
.
![]() . These functions have been chosen because they seem to illustrate the general situation, but still give computations which are within reach. Even with only slightly more complicated functions (e.g. polynomials of higher degree) I have not been able to complete the computations within reasonable time.
. These functions have been chosen because they seem to illustrate the general situation, but still give computations which are within reach. Even with only slightly more complicated functions (e.g. polynomials of higher degree) I have not been able to complete the computations within reasonable time.
In the next section, I will instead turn to rigorous methods for proving general theorems about these phenomena.
4. A Weak Theorem about Rotation
In view of the numerics of the previous section, it would be tempting to conjecture that it is a general fact for the kind of classical strings of this paper, that curvature in the sense of (1.1) can be diminished by letting them rotate in such a way that the ends move with (approximately) the speed of light. (In the limit of very thin strings, one would even suspect that the word “approximately” could be replaced by “exactly”). However, one should be careful when making predictions from this kind of numerical computations. In any case, to decide what actually happens may turn out to be a very difficult problem.
In this section I will prove a weaker result, namely that for any function ![]() as in Section 3, in the limit
as in Section 3, in the limit![]() , the corresponding non-rotating string is not curvature minimizing. More precisely, I will prove:
, the corresponding non-rotating string is not curvature minimizing. More precisely, I will prove:
Theorem 1. For any![]() ,
, ![]() sufficiently small and the metric
sufficiently small and the metric ![]() as in (3.2) above, the second derivative of the function
as in (3.2) above, the second derivative of the function ![]() at
at ![]() is strictly negative.
is strictly negative.
This should be compared with the corresponding situation in Euclidian geometry. In fact, if we replace the metric in (3.2) above by
![]() (4.1)
(4.1)
then we have
Theorem 2. For any![]() ,
, ![]() sufficiently small and the metric
sufficiently small and the metric ![]() as in (4.1) above, the second derivative of the function
as in (4.1) above, the second derivative of the function ![]() at
at ![]() is strictly positive.
is strictly positive.
The proof of Theorem 2 is very similar to the proof of Theorem 1, hence will be omitted (see however (4.6) below).
Proof: To prove Theorem 1, we need to compute the scalar curvature ![]() for the metric in (3.2). Although this is in principle strait forward, the computations become very heavy, and are in fact most easily carried out on a computer. Here I will only sketch the main steps. Also, note that the contributions from the two ends
for the metric in (3.2). Although this is in principle strait forward, the computations become very heavy, and are in fact most easily carried out on a computer. Here I will only sketch the main steps. Also, note that the contributions from the two ends ![]() and
and ![]() are obviously equal, hence it is enough to consider
are obviously equal, hence it is enough to consider![]() .
.
Due to the special diagonal form of the metric in (3.2), a comparatively short computation gives that
![]() (4.2)
(4.2)
Inserting the expression for ![]() in (3.1) into (4.2), we obtain after a somewhat longer computation that
in (3.1) into (4.2), we obtain after a somewhat longer computation that
![]() (4.3)
(4.3)
where ![]() are in fact all functions of
are in fact all functions of![]() . Computing the second derivative with respect to
. Computing the second derivative with respect to ![]() of
of ![]() and then putting
and then putting![]() , after a very long computation gives
, after a very long computation gives
![]() (4.4)
(4.4)
where ![]() now has become equal to
now has become equal to![]() . Taylor expanding this expression with respect to
. Taylor expanding this expression with respect to ![]() (and noting that the zero and first order terms vanish) we obtain
(and noting that the zero and first order terms vanish) we obtain
![]() (4.5)
(4.5)
Note that the use of the metric (4.1) would instead give
![]() (4.6)
(4.6)
To prove the claim, it is enough to prove that the integral of the coefficient for![]() , i.e.
, i.e.
![]() (4.7)
(4.7)
is strictly negative (note the extra factor 2 since we only integrate over one of the balls). Making the trivial change of coordinates![]() , and continuing to write
, and continuing to write ![]() for
for![]() , we obtain
, we obtain
![]() (4.8)
(4.8)
Next, observe that
![]() (4.9)
(4.9)
for simple reasons of symmetry, since ![]() is an odd function whereas the rest of the integrand is even in
is an odd function whereas the rest of the integrand is even in![]() . Hence the integral reduces to
. Hence the integral reduces to
![]() (4.10)
(4.10)
Furthermore, we note that, again for obvious symmetry reasons,
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
![]() (4.13)
(4.13)
which clearly implies that
![]() (4.14)
(4.14)
![]() (4.15)
(4.15)
In fact, since![]() , the sum of the three integrals in (4.11), (4.12) and (4.13) equals the integral in (4.15) from which the claim follows. Inserting this into (4.10), we obtain
, the sum of the three integrals in (4.11), (4.12) and (4.13) equals the integral in (4.15) from which the claim follows. Inserting this into (4.10), we obtain
![]() (4.16)
(4.16)
which is clearly non-positive. Finally, to prove that ![]() is strictly negative, we simply observe that to demand the right-hand side of (4.16) to be zero would require
is strictly negative, we simply observe that to demand the right-hand side of (4.16) to be zero would require ![]() to satisfy the differential equation
to satisfy the differential equation![]() . But the general solution to this equation is
. But the general solution to this equation is
![]() (4.17)
(4.17)
and no such function satisfies the conditions ![]() of Section 3.
of Section 3.
5. Conclusions and Further Developments
The calculations in this paper are obviously only a first step towards understanding why curvature is diminished by rotations in Lorentz geometry. The simple kind of rotation used here should of course in the future be replaced by a physically better motivated one. However, presently it is not clear how this should be done. In fact, it may be that when we leave the context of Euclidian Geometry and general relativity as defined by Einstein’s traditional field equations, it can be impossible to define rotations in a consistent way. The approach which to my mind seems to be the most promising one is to start from the minimizing principle (1.1) and then show that minimizing solutions will in fact have properties similar to ordinary rotations. However, this will first of all require making this principle more precise, and in addition we will have to deal with mathematical difficulties of a different order of magnitude as compared to the ones encountered in this paper.
Probably, an easier kind of generalization would be to do without the expansion in ![]() (i.e. to weaken the requirement that the deviation from the flat metric should be small) but still restrict to infinitesimal speed
(i.e. to weaken the requirement that the deviation from the flat metric should be small) but still restrict to infinitesimal speed ![]() of rotation. Also, one can try to consider more general metrics than the ones in Theorem 1. In particular it would be interesting to see if one could find a non-trivial rotation metric (in a sense yet to be made precise) which coincides with the flat one outside the string, but which does not satisfy the other requirements, and does not exhibit the typical behavior in Theorem 1.
of rotation. Also, one can try to consider more general metrics than the ones in Theorem 1. In particular it would be interesting to see if one could find a non-trivial rotation metric (in a sense yet to be made precise) which coincides with the flat one outside the string, but which does not satisfy the other requirements, and does not exhibit the typical behavior in Theorem 1.
Finally, one can try to generalize the ideas of this paper to topologically non-trivial situations, e.g. to rotating worm-holes. For a (non-rigorous) attempt in this direction, see [6] .